2. 中国科学院大学,北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
精密单点定位(PPP)[1-4]因仅利用单台GNSS接收机即可实现全球范围内高精度绝对定位的优点而得到广泛的研究与应用。传统的基于消电离层组合模型的精密单点定位,由于卫星端和接收机端相位偏差的影响,导致其模糊度参数失去整数特性,限制了定位精度的提高。为提高定位精度,许多学者对精密单点定位模糊度固定(PPP ambiguity resolution,PPP-AR)进行了深入研究。
常用的PPP-AR方法一般分为3类,即小数周偏差法、整数相位钟法和钟差解耦法[5-7],已有研究证明这3类方法是等价的[8-9]。小数周偏差法直接估计宽巷与窄巷模糊度的小数偏差部分,用户可直接利用偏差产品实现模糊度固定[10-12],但是该方法需对不同分析中心的钟差分别估计相应的小数偏差产品。整数相位钟法也需宽巷模糊度偏差产品固定宽巷模糊度,与小数周偏差法不同的是,该方法通过钟差将窄巷模糊度偏差吸收,构造相位钟,用户固定宽巷模糊度后,只需使用该钟差产品即可实现模糊度固定[13-18]。钟差解耦法对窄巷模糊度偏差的处理策略与整数相位钟法相同,但该方法更加注重偏差参数的时变特性,分别为伪距、相位及宽巷模糊度观测量估计钟差参数,得到解耦钟,用户使用这3类钟差即可获得先固定宽巷、后固定窄巷的PPP固定解[19-22]。
在实际研究中,因为钟差解耦模型服务端与用户端的实现算法相对较为复杂,导致目前对于PPP-AR的研究主要集中在小数周偏差法和整数相位钟法[23-25]。但是,相比于将宽巷模糊度偏差在天内视为常数,钟差解耦模型则顾及其时变特性并对其逐历元估计,因而能够更好地反映该参数的真实状态,有利于进一步深入研究该类偏差的时变特性。此外,由于GNSS观测量中的码偏差(包括伪距硬件延迟、多路径效应及未模型化的伪距误差)是导致钟差产生“天跳变”的主要原因之一,因此,钟差解耦模型对于伪距钟和相位钟的解耦可以较好地避免上述问题[19]。近年来,笔者在深入分析和研究钟差解耦模型的过程中发现,虽然解耦钟差为该模型的主要特色,但是基于该模型的卫星钟差很少有公开的研究报道。以往的有关研究显示时变卫星码偏差阻碍了滤波器的快速收敛,提取码偏差可以使钟差更快地达到稳定[26]。由于钟差解耦模型对钟差的解耦,因而可有效避免时变卫星码偏差对滤波器收敛速度的限制。
为此,本文从基础理论、方法及试验验证等多方面分析和深入研究了钟差解耦模型卫星钟差估计的快速收敛优势及宽巷模糊度偏差参数的时变特性。
1 数学模型与分析方法本节主要从消电离层组合观测值出发,分别导出传统消电离层模型和钟差解耦模型,分析两种模型钟差的重构差异,在文献[26]的基础上重新梳理导出提取卫星码偏差(satellite code bias,SCB)的钟差估计模型,深入分析和研究钟差解耦模型在钟差估计收敛速度方面的优势。
1.1 消电离层组合模型与钟差解耦模型GPS双频消电离层组合观测方程可以表示为
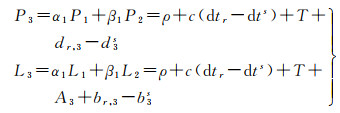 (1)
(1)
式中,P1、P2和L1、L2分别表示各频率原始伪距及相位观测值,单位为m;P3和L3分别表示消电离层伪距和相位观测值;ρ表示站星距;c表示光在真空中的传播速度;dtr和dts分别表示接收机钟差和卫星钟差;T表示斜向对流层延迟;A3表示消电离层后的模糊度,单位为m;dr, 3和d3s分别表示消电离层接收机和卫星码偏差;br, 3和b3s分别表示消电离层接收机和卫星相位偏差。假设其他误差已经改正,并且为了形式简化,观测噪声等误差在此忽略。另外,定义频率为f1和f2,式(1)中其他参数表示为
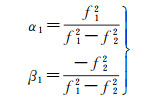
顾及码偏差和相位偏差都具有的时变特性,可将这些偏差描述为时不变部分与时变部分的组合[15]
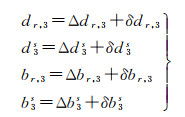 (2)
(2)
式中,Δ和δ分别表示时不变部分和时变部分。
在式(1)中,钟差项与偏差项的线性相关导致方程列秩亏,通常采用的消秩亏方法是参数重组,组合钟差与码偏差为新钟差参数,模糊度吸收相位偏差。假设模糊度A3是严格不变的实数,则在伪距观测方程中,如果钟差将码偏差全部吸收,时变码偏差必将会对相位观测方程产生影响。并且由于相位观测方程相对于伪距观测方程的权重较高,因此,该类时变偏差必然会引起模糊度的扰动,而这与假设不相符。同样,在相位观测方程中为了避免时变相位偏差对模糊度的扰动,钟差也需要对其吸收。据此,整合式(1)和式(2)可得传统的消电离层组合模型为
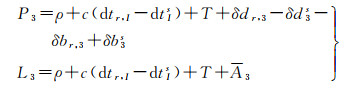 (3)
(3)
式中
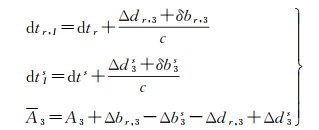
需要注意的是,式(3)严格成立的前提条件是模糊度为严格不变的实数,但在实际计算中,模糊度的估值在历元间通常会有稍许变化,加之,观测方程的误差项等描述也会与实际有不同程度的差异(如未模型化误差、随机模型误差等),导致时变偏差一般会对其他参数产生扰动影响[26-27]。
不同于传统消电离层组合模型中伪距观测值与相位观测值共用相同的钟差,钟差解耦模型中不同类型的观测值对应不同的钟差,这也简化了钟差参数的重组过程,即无须考虑偏差的时变特性,各类观测值的钟差直接吸收相应偏差即可。为此,可将参数重组后的伪距观测值与相位观测值方程表示为
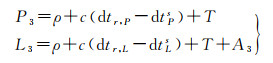 (4)
(4)
式中
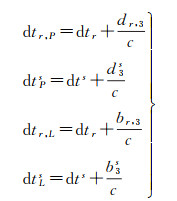
为了便于模糊度固定,将模糊度参数改写为宽巷与窄巷模糊度的组合形式
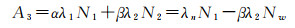 (5)
(5)
式中,λ1和λ2分别为第一频率和第二频率的波长;N1和N2分别表示两个频率上的模糊度参数,单位为周;λn=c/(f1+f2)表示窄巷模糊度波长;Nw=N1-N2表示宽巷模糊度。
Melbourne-Wübbena组合观测值[28-31]为
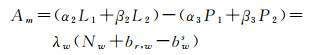 (6)
(6)
式中
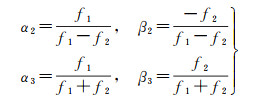
且
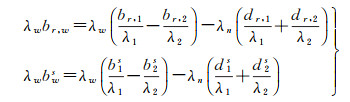
联立式(4)、式(5)和式(6)即可得到钟差解耦模型为
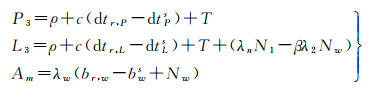 (7)
(7)
对不同类型观测值的钟差进行解耦,模糊度与钟差参数之间仍存在线性相关。在用户端,初始历元直接指定特定卫星的模糊度值为任意整数即可消除秩亏。在服务端,首先需要选定接收机钟差稳定的测站,将其3类钟差设定为0作为基准,然后依次选定模糊度作为基准来消除其与钟差之间的线性相关。PPP网解中模糊度基准的选定方案已被系统研究,具体可参考文献[2, 32—33]。
1.2 提取卫星码偏差的钟差估计模型卫星码偏差是限制卫星钟差收敛速度的主要因素,将其提取后可显著提升钟差的收敛速度及收敛后的稳定性[26]。这里所谓提取卫星码偏差,即不再通过卫星钟差吸收码偏差,而是将其作为一个独立的参数估计。顾及各参数的时变特性,用i表示相应的历元,则可将式(1)改写为
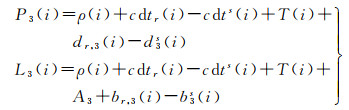 (8)
(8)
与传统消电离层组合模型相比,该模型仅对卫星码偏差的处理方式不同,对其他参数重组可得
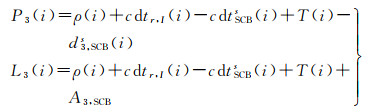 (9)
(9)
式中
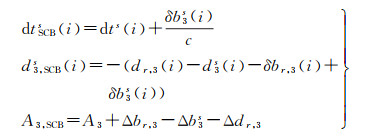
显然,式(9)中卫星码偏差、钟差及模糊度之间的线性相关导致方程秩亏,为此,选定首历元的卫星码偏差作为基准,即将其设定为0,因此,对于非首历元的观测方程为
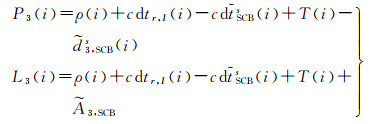 (10)
(10)
式中
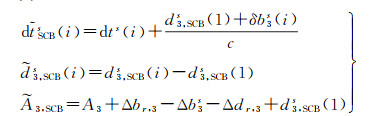
式(10)为提取卫星码偏差的钟差估计模型,其中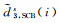
钟差的精度评定通常采用二次差法。由于钟差解耦模型可以得到不同类型的钟差,因此不同类型钟差之间的二次差分序列也值得深入分析和研究。首先通过星间单差消除公共基准,假设选定卫星n作为参考星,m表示其他卫星,则对于IGS钟差及解耦伪距钟和相位钟有如下形式
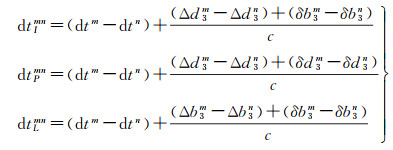
分别将伪距钟和相位钟与IGS钟作差分,并将伪距钟与相位钟作差分,可获得如下表达式
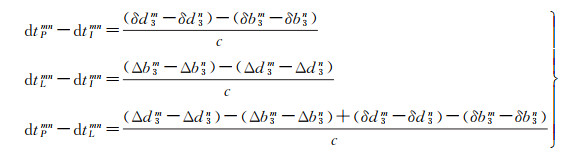 (11)
(11)
由式(11)可知,伪距钟与IGS钟的差值和伪距钟与相位钟的差值具有相同的时变项,虽然这两类差分序列的真实状态会被伪距钟所包含的伪距观测噪声掩盖,但其时间序列应表现出一致性。
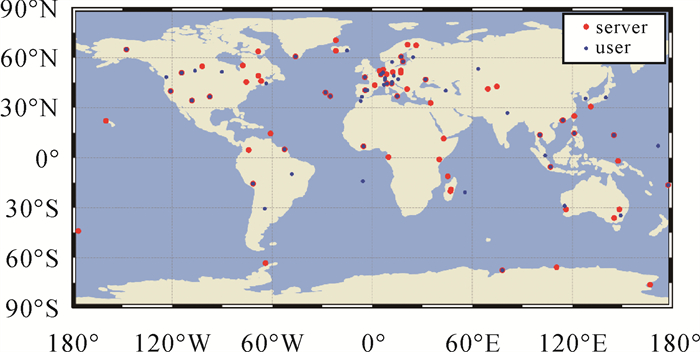
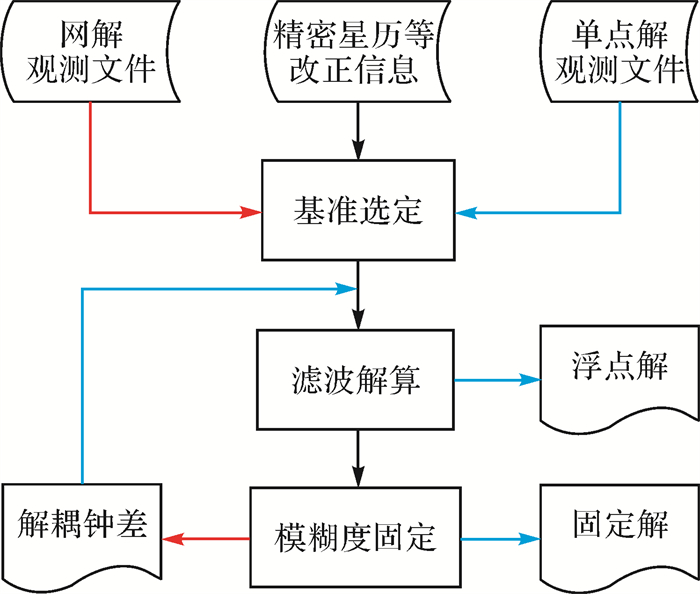
2 数据处理试验数据集选取IGS观测站2021年DOY 031— DOY 037的双频GPS观测数据,采样间隔为30 s。各测站在全球的分布情况如图 1所示,其中,红色圆点表示用于服务端估计解耦钟差产品的测站,蓝色的圆点表示用于PPP测试的测站。钟差解耦模型服务端及用户端的数据处理如图 2所示,其中,红色表示网解部分,蓝色表示单点解部分,黑色表示公共部分。在服务端网解,首先准备观测数据及必要的改正文件,然后选定基准进行滤波解算,经模糊度固定后即可得到解耦钟差产品。在用户端单点解,选定模糊度基准后,利用解耦钟差产品进行滤波解算,获得模糊度浮点解和固定解。
|
| 图 1 测站选取分布 Fig. 1 Distribution of the experimental stations |
|
| 图 2 钟差解耦模型网解及单点解数据处理 Fig. 2 Network and single point data processing based on decoupled clock model |
试验中,数据处理策略总体可概括为:测站坐标在服务端固定为IGS周解坐标,在用户端作为白噪声参数估计;钟差作为白噪声参数估计;天顶对流层干延迟通过Saastamoinen模型[34]改正,湿延迟作为随机游走参数估计;模糊度在连续弧段内作为常数估计;卫星的截至高度角设置为10°;伪距和相位观测值的先验中误差分别设定为0.3 m和0.003 m,并根据误差传播律构建3类观测值(伪距、相位及宽巷模糊度)的随机模型。在模糊度固定策略方面:分别固定宽巷和窄巷模糊度得到模糊度固定解,宽巷模糊度在其标准差及小数部分低于0.15周时直接取整得到,并设定模糊度追踪策略,仅连续固定到同一整数超过5个历元方可视为固定;窄巷模糊度需在成功率[35]检验后通过方可固定,成功率设定为99.9%,随后采用MLAMBDA方法[36-37]搜索模糊度,并对其进行Ratio[38]检验,阈值设定为2.0。
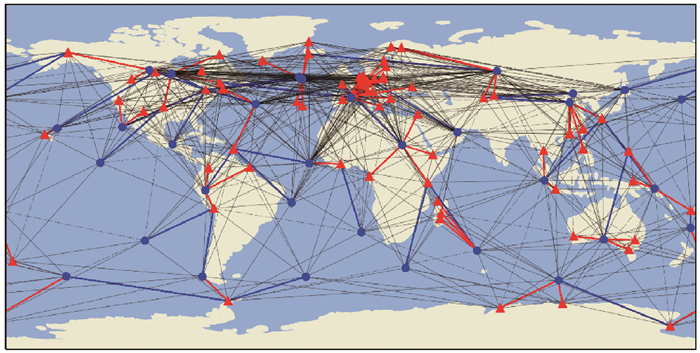
3 试验分析本节从解耦钟的收敛速度、解耦钟的精度及基于解耦钟的PPP-AR 3方面分别展开试验分析和研究。单天观测数据估计的解耦钟用于收敛速度测试,而后两部分试验所使用的解耦钟则需利用前一天的观测数据使解耦钟充分收敛。模糊度基准的合理选取是钟差解耦模型满秩的重要保证。图 3为模糊度基准选取图。由于使用前一天的观测数据保证滤波收敛,图 3为2021年DOY 030 22时(初始时刻)的模糊度基准初始化情况。其中,红色三角表示用于网解的观测站,蓝色圆点表示卫星,蓝色实线表示使卫星钟差独立可估的模糊度基准,红色实线表示使接收机钟差独立可估的模糊度基准,黑色实线表示当前历元待估模糊度参数,黑色虚线表示卫星被剔除。
|
| 图 3 服务端模糊度基准选取 Fig. 3 Ambiguity datum initialization at the server end |
3.1 解耦钟的收敛速度
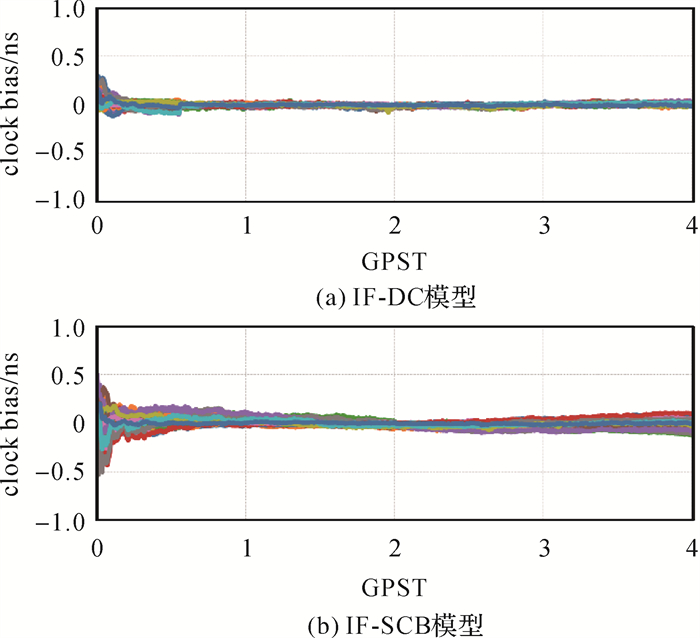
文献[26]分析了在钟差估计中,时变卫星码偏差限制了滤波器初始化的速度,且收敛后会在较长时间内持续影响钟差的稳定性,而提取SCB后,上述不利影响可明显改善。在解耦钟差模型中,时变SCB可完全被伪距钟差吸收,但是由于伪距观测方程并未与相位方程对齐,导致其精度较低,无法与传统消电离层组合得到的钟差进行有效比较。因此,通常可以通过比较相位钟与提取SCB后的钟差,反映估计解耦钟差时滤波器的收敛速度及收敛后的钟差稳定性。图 4为钟差估计系统开始后4 h内解耦钟差相位钟(IF-DC)与基于传统消电离层组合提取SCB后得到的钟差相对于IGS最终产品的偏差时间序列,其中,G01卫星为参考星。图中显示,IF-DC模型估计的钟差在滤波开始较短时间内即可收敛,并且在后续估计中表现出较高的稳定性,而IF-SCB模型估计的钟差需要1 h左右可完成收敛过程,并且在第3~4 h之间并不十分稳定。
|
| 图 4 2021年DOY 031不同模型的钟差产品相对于IGS最终产品4 h的偏差时间序列 Fig. 4 Four hour time series of the clock biases with respect to the IGS final products on DOY 031 in 2021 |
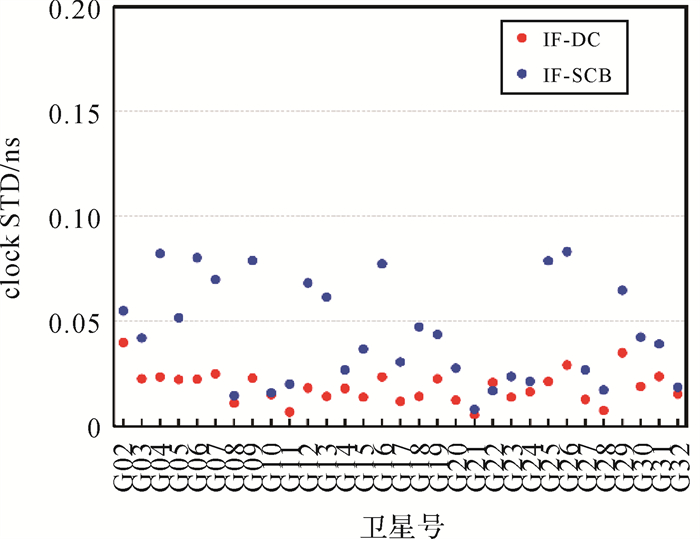
由于上述两类钟差的物理含义不同,因此,仅统计上述两类钟差偏差的标准偏差(standard deviation,STD)来反映其稳定性,如图 5所示。从图中可以看出,除了少数卫星两类钟差的STD较为接近外,其他大部分卫星的相位钟在稳定性上都优于IF-SCB模型估计的钟差,约为0.025 ns。上述结果表明,在钟差估计系统因网络等原因意外中断后,钟差解耦模型可以更快地提供稳定的产品,能有效辅助用户快速恢复高精度定位。
|
| 图 5 2021年DOY 031不同模型的钟差产品相对于IGS最终产品的前4 h偏差的标准差 Fig. 5 STD of 4 h clock estimates compared with the IGS final products on DOY 031 in 2021 |
3.2 解耦钟的精度
以往的研究尚未有效评估和分析解耦钟差产品的性能。为此,本文试验选用IGS最终产品作为标准对解耦钟差产品精度和可靠性进行评定。图 6为解耦卫星钟的差分时间序列,其中,G01卫星为参考星,Code-IGS、Phase-IGS、Code-Phase分别对应式(11)中的3组方程,WL bias表示宽巷模糊度钟(偏差),它仅移除了基准。为方便观察,每一时间序列均移除其平均值。
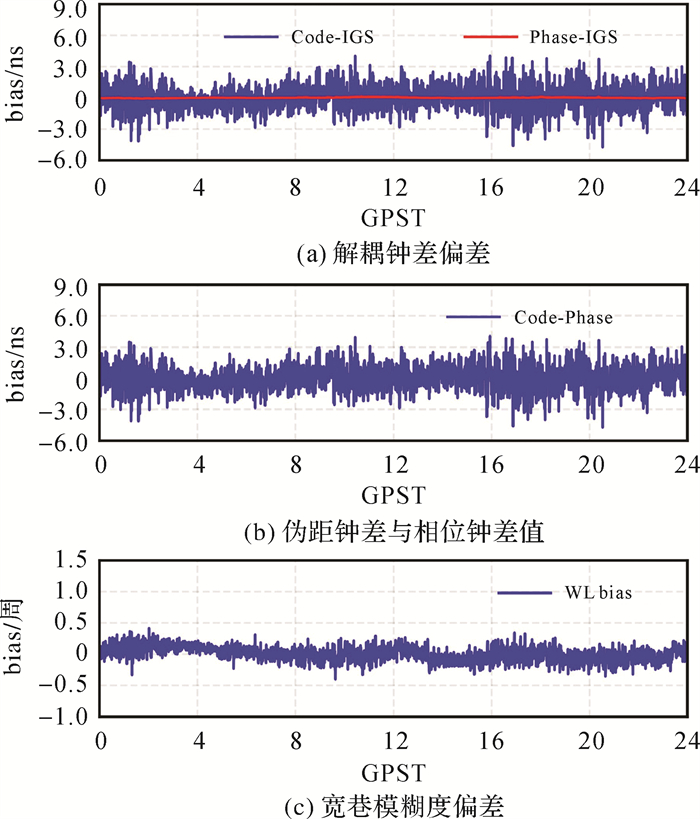
|
| 图 6 2021年DOY 031 G02卫星的解耦钟差偏差时间序列 Fig. 6 Time series of G02 decoupled clock biases on DOY 031 in 2021 |
图 6(a)、(b)中,蓝色曲线表示的时间序列印证了对式(11)的分析,即Code-IGS与Code-Phase具有类似的时变趋势。由于对伪距钟与相位钟进行了解耦计算,伪距钟差估值表示出了强烈的噪声特性。相对于伪距钟差估值,相位钟差估值则表现出较高的稳定性。宽巷模糊度偏差估值也较为稳定。
对钟差精度的评价的指标通常选择STD和RMS,其中,STD表征钟差相对于参考标准的稳定性,RMS表征钟差相对于参考标准的偏移程度。由于解耦钟差与IGS钟差具有不同的物理含义,因此,在此仅通过STD来反映解耦钟差的稳定性。图 7统计了所有卫星关于图 6中解耦钟偏差序列的STD。相位钟估值表现出较高的稳定性,平均约为0.02 ns,而伪距钟估值由于较强的噪声影响,其平均值约为1.15 ns,宽巷模糊度偏差估值平均STD则约为0.12周。

|
| 图 7 2021年DOY 031卫星的解耦钟差偏差的标准差 Fig. 7 STD of decoupled clock biases on DOY 031 in 2021 |
钟差解耦模型将宽巷模糊度偏差作为时变参数,并将其作为白噪声参数估计,因此,可以分析单天内宽巷模糊度偏差的时变特性。2021年DOY 031所有卫星的宽巷模糊度偏差估值如图 8所示。为减小刻度范围,便于观察其稳定性,所有偏差序列均被偏移整数周以将其限制在0~10周范围内。由图 8可以看出,各卫星的宽巷模糊度偏差估值序列在天内表现出明显的噪声特性,这是因为在服务端网解中该偏差项被建模为白噪声参数所致。但是对于每颗卫星而言,它们的宽巷模糊度偏差估值均围绕某一常数波动,这说明卫星的宽巷模糊度偏差在天内是稳定的。

|
| 图 8 2021年DOY 031卫星的宽巷模糊度偏差时间序列 Fig. 8 Time series of wide-lane ambiguity biases on DOY 031 in 2021 |
目前,IGS分析中心CNES/CLS提供整数相位钟与天解宽巷模糊度偏差产品用于模糊度固定,其中,各卫星的宽巷模糊度偏差保存在CNES/CLS钟差产品的头文件中。与本文提供的天内时变宽巷模糊度偏差序列不同,CNES/CLS将该偏差项作为天常数,即单天内为每颗卫星提供单个偏差改正[13]。为客观分析钟差解耦模型估计的宽巷模糊度偏差精度,本试验以CNES/CLS的产品为标准进行对比分析。二次差分(G01为参考星)并移除整周模糊度后的互差值如图 9所示。由于观测噪声的影响,各差值序列均围绕0附近波动。统计其平均差值约为-0.058周。统计图 9中各卫星二次差分时间序列(共计89 280个样本)得到图 10,以分析其互差分布情况。由图 10可知,宽巷模糊度互差值总体而言满足期望为-0.058周的正态分布,并且大部分互差值分布在±0.2周之内。与现有研究结论相比,该互差值略大,究其原因,一方面是因为钟差解耦模型无须将宽巷模糊度逐历元平滑,没有破坏其固有的时变特性,另一方面,将宽巷模糊度偏差建模为白噪声参数进行逐历元参数估计,也是造成其与CNES/CLS产品互差值较大的原因。
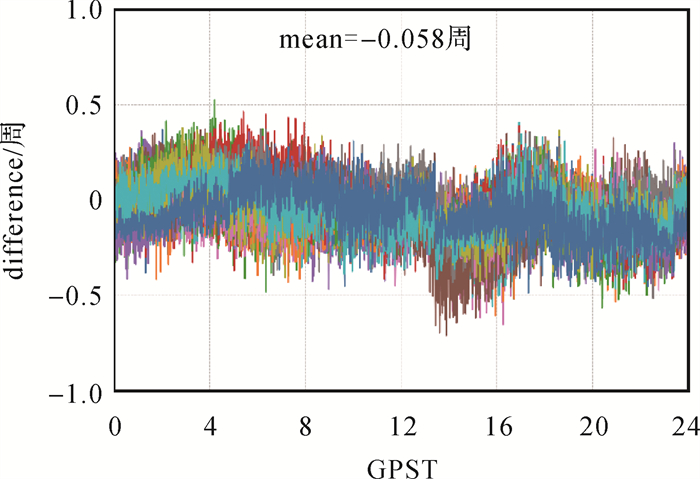
|
| 图 9 2021年DOY 031卫星的宽巷模糊度偏差估值相对于CNES/CLS产品的差异 Fig. 9 The wide-lane bias differences between estimates and CNES/CLS products on DOY 031 in 2021 |
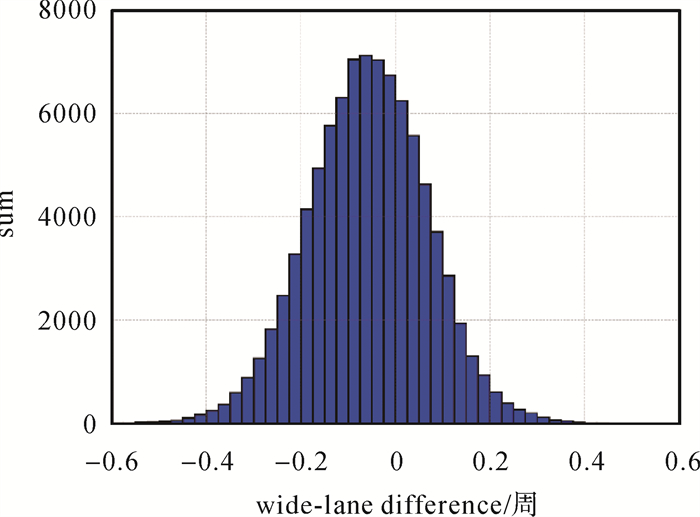
|
| 图 10 2021年DOY 031卫星的宽巷模糊度偏差估值与CNES/CLS产品互差分布直方图 Fig. 10 Histogram of the difference between estimates and CNES/CLS products on DOY 031 in 2021 |
3.3 定位效果分析
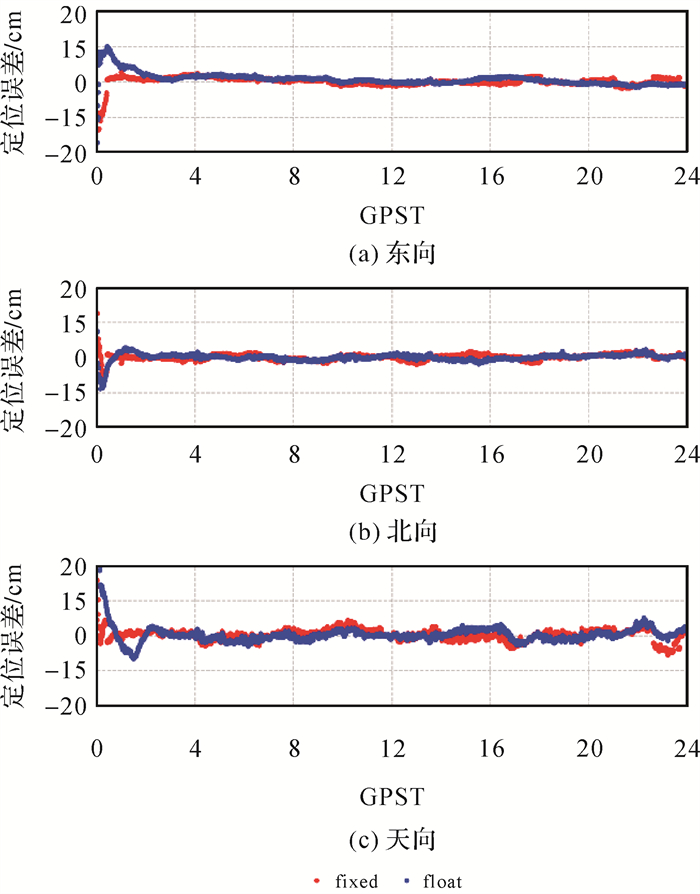
为了验证解耦钟差产品实际定位效果,对图 1所示所有用户站7 d的观测数据进行定位分析,获得模糊度固定解(fixed),同时使用IGS最终钟差产品进行定位测试获得模糊度浮点解(float)。IGS周解坐标文件作为真值比较和评估两种定位方式的定位精度。为了直观比较两种定位方式的误差情况,图 11展示了SASK测站模糊度固定解与浮点解的定位误差对比。当模糊度固定成功后,定位误差迅速到达0附近。在浮点解收敛后,其与固定解的定位精度较为接近。
|
| 图 11 2021年DOY 031 SASK测站模糊度固定解与浮点解定位误差对比 Fig. 11 Positioning errors of fixed and float PPP solutions of SASK station on DOY 031 in 2021 |
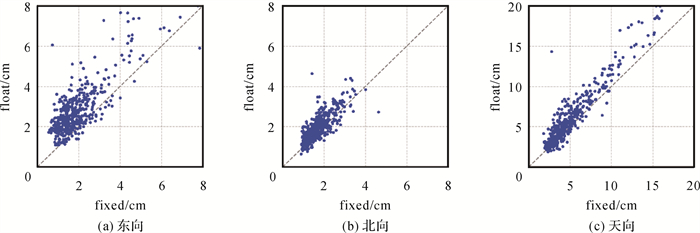
对7 d两种定位模式的定位误差RMS值统计得到图 12。图中每1个点表示1个测站单天定位误差的RMS值。图中显示,在北向和天向,模糊度固定后精度略有提升,相比较而言,东向提升的效果更为明显。对各天两种定位模式下的平均RMS进行统计可得到表 1。由表 1可以看出,模糊度固定解相对浮点解在各天东方向的精度提升基本优于30%,平均提升为31.57%,在北方向和天向分别为12.09%和16.31%。
|
| 图 12 2021年DOY 031—DOY 037各测站固定解与浮点解定位误差RMS值对比 Fig. 12 RMS of fixed solutions in contrast to those with float solutions for each station from DOY 031 to DOY 037 in 2021 |
| 年积日 | 固定解/cm | 浮点解/cm | 精度提升/(%) | ||||||||
| 东向 | 北向 | 天向 | 东向 | 北向 | 天向 | 东向 | 北向 | 天向 | |||
| 031 | 1.96 | 1.54 | 4.93 | 2.81 | 1.86 | 6.11 | 30.25 | 17.20 | 19.31 | ||
| 032 | 2.14 | 1.83 | 6.54 | 2.99 | 2.08 | 7.83 | 28.43 | 12.02 | 16.48 | ||
| 033 | 2.05 | 1.69 | 5.27 | 2.97 | 1.92 | 6.17 | 30.98 | 11.98 | 14.59 | ||
| 034 | 1.87 | 1.75 | 5.12 | 2.91 | 2.01 | 6.27 | 35.74 | 12.94 | 18.34 | ||
| 035 | 2.29 | 1.80 | 5.83 | 3.32 | 2.02 | 6.68 | 31.02 | 10.89 | 12.72 | ||
| 036 | 1.63 | 1.64 | 4.99 | 2.64 | 1.90 | 6.04 | 38.26 | 13.68 | 17.38 | ||
| 037 | 1.91 | 1.82 | 5.54 | 2.60 | 1.94 | 6.57 | 26.54 | 6.19 | 15.68 | ||
| 平均 | 1.98 | 1.72 | 5.46 | 2.89 | 1.96 | 6.52 | 31.57 | 12.09 | 16.31 | ||
4 结论
钟差解耦模型是一种重要的模糊度固定模型,但以往的研究却很少涉及对该模型的研究。本文详细回顾了钟差解耦模型,给出了服务端网解和用户端单点解数据处理策略,深入研究了钟差解耦模型的特点及优势。
文中首先对比了传统消电离层组合模型、提取卫星码偏差模型和钟差解耦模型在钟差构造上的不同,分析了时变卫星码偏差对3种模型的影响,比较了后两种模型在钟差估计收敛速度及稳定性上的差异;然后评定了解耦钟差产品的精度,并重点分析了宽巷模糊度偏差的天内时变特性;最后基于解耦钟差产品进行PPP-AR试验。结果表明,相比于提取卫星码偏差模型,钟差解耦模型在钟差估计中具有更快的收敛速度,且钟差产品更加稳定,以4 h的收敛过程为例,解耦相位钟的稳定性可达到0.025 ns;解耦钟差产品具有较高的精度,其中相位钟的稳定性约为0.02 ns,宽巷模糊度偏差在天内较为稳定,以CNES/CLS最终产品作为标准,天内平均偏差约为-0.058周,且大部分偏差集中在±0.2周之内;基于解耦钟差产品的模糊度固定解可显著提升定位精度,特别是在东方向上,精度提升可达到30%。
下一步将在GPS系统钟差解耦模型研究的基础上,深入开展基于多系统特别是北斗卫星导航系统的钟差解耦精密单点定位模糊度固定模型等方面的研究。
| [1] |
KOUBA J, HÉROUX P. Precise point positioning using IGS orbit and clock products[J]. GPS Solutions, 2001, 5(2): 12-28. DOI:10.1007/PL00012883 |
| [2] |
LIU Shuai, YUAN Yunbin. Generating GPS decoupled clock products for precise point positioning with ambiguity resolution[J]. Journal of Geodesy, 2022, 96(1): 6. DOI:10.1007/s00190-021-01593-7 |
| [3] |
李博峰, 葛海波, 沈云中. 无电离层组合、Uofc和非组合精密单点定位观测模型比较[J]. 测绘学报, 2015, 44(7): 734-740. LI Bofeng, GE Haibo, SHEN Yunzhong. Comparison of ionosphere-free, Uofc and uncombined PPP observation models[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7): 734-740. DOI:10.11947/j.AGCS.2015.20140161 |
| [4] |
张小红, 胡家欢, 任晓东. PPP/PPP-RTK新进展与北斗/GNSS PPP定位性能比较[J]. 测绘学报, 2020, 49(9): 1084-1100. ZHANG Xiaohong, HU Jiahuan, REN Xiaodong. New progress of PPP/PPP-RTK and positioning performance comparison of BDS/GNSS PPP[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(9): 1084-1100. DOI:10.11947/j.AGCS.2020.20200328 |
| [5] |
GE M, GENDT G, ROTHACHER M, et al. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations[J]. Journal of Geodesy, 2008, 82(7): 389-399. DOI:10.1007/s00190-007-0187-4 |
| [6] |
LAURICHESSE D, MERCIER F, BERTHIAS J P, et al. Integer ambiguity resolution on undifferenced GPS phase measurements and its application to PPP and satellite precise orbit determination[J]. Navigation, 2009, 56(2): 135-149. DOI:10.1002/j.2161-4296.2009.tb01750.x |
| [7] |
COLLINS P, LAHAYE F, HÉROUX P, et al. Precise point positioning with ambiguity resolution using the decoupled clock model[C]//Proceedings of the 21st International Technical Meeting of the Satellite Division of the Institute of Navigation. Savannah, GA, USA: [s. n. ], 2008: 1315-1322.
|
| [8] |
GENG Jianghui, MENG Xiaolin, DODSON A H, et al. Integer ambiguity resolution in precise point positioning: method comparison[J]. Journal of Geodesy, 2010, 84(9): 569-581. DOI:10.1007/s00190-010-0399-x |
| [9] |
SHI Junbo, GAO Yang. A comparison of three PPP integer ambiguity resolution methods[J]. GPS Solutions, 2014, 18(4): 519-528. DOI:10.1007/s10291-013-0348-2 |
| [10] |
GENG Jianghui, SHI Chuang, GE Maorong, et al. Improving the estimation of fractional-cycle biases for ambiguity resolution in precise point positioning[J]. Journal of Geodesy, 2012, 86(8): 579-589. DOI:10.1007/s00190-011-0537-0 |
| [11] |
LI Pan, ZHANG Xiaohong, REN Xiaodong, et al. Generating GPS satellite fractional cycle bias for ambiguity-fixed precise point positioning[J]. GPS Solutions, 2016, 20(4): 771-782. DOI:10.1007/s10291-015-0483-z |
| [12] |
LI Xingxing, HAN Xinjuan, LI Xin, et al. GREAT-UPD: an open-source software for uncalibrated phase delay estimation based on multi-GNSS and multi-frequency observations[J]. GPS Solutions, 2021, 25(2): 66. DOI:10.1007/s10291-020-01070-2 |
| [13] |
LOYER S, PEROSANZ F, MERCIER F, et al. Zero-difference GPS ambiguity resolution at CNES-CLS IGS analysis center[J]. Journal of Geodesy, 2012, 86(11): 991-1003. DOI:10.1007/s00190-012-0559-2 |
| [14] |
刘帅, 孙付平, 郝万亮, 等. 整数相位钟法精密单点定位模糊度固定模型及效果分析[J]. 测绘学报, 2014, 43(12): 1230-1237. LIU Shuai, SUN Fuping, HAO Wanliang, et al. Modeling and effects analysis of PPP ambiguity fixing based on integer phase clock method[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(12): 1230-1237. DOI:10.13485/j.cnki.11-2089.2014.0195 |
| [15] |
GENG Jianghui, CHEN Xingyu, PAN Yuanxin, et al. A modified phase clock/bias model to improve PPP ambiguity resolution at Wuhan University[J]. Journal of Geodesy, 2019, 93(10): 2053-2067. DOI:10.1007/s00190-019-01301-6 |
| [16] |
KATSIGIANNI G, LOYER S, PEROSANZ F. PPP and PPP-AR kinematic post-processed performance of GPS-only, Galileo-only and multi-GNSS[J]. Remote Sensing, 2019, 11(21): 2477. DOI:10.3390/rs11212477 |
| [17] |
DUAN Bingbing, HUGENTOBLER U. Comparisons of CODE and CNES/CLS GPS satellite bias products and applications in Sentinel-3 satellite precise orbit determination[J]. GPS Solutions, 2021, 25(4): 128. DOI:10.1007/s10291-021-01164-5 |
| [18] |
SCHAER S, VILLIGER A, ARNOLD D, et al. The CODE ambiguity-fixed clock and phase bias analysis products: generation, properties, and performance[J]. Journal of Geodesy, 2021, 95(7): 81. DOI:10.1007/s00190-021-01521-9 |
| [19] |
COLLINS P, BISNATH S, LAHAYE F, et al. Undifferenced GPS ambiguity resolution using the decoupled clock model and ambiguity datum fixing[J]. Navigation, 2010, 57(2): 123-135. |
| [20] |
SHI Junbo, GAO Yang. Analysis of the integer property of ambiguity and characteristics of code and phase clocks in PPP using a decoupled clock model[C]//Proceedings of the 23rd International Technical Meeting of the Satellite Division of the Institute of Navigation. Portland, OR, USA: [s. n. ], 2010: 2553-2564.
|
| [21] |
BANVILLE S, GENG J H, LOYER S, et al. On the interoperability of IGS products for precise point positioning with ambiguity resolution[J]. Journal of Geodesy, 2020, 94(1): 10. DOI:10.1007/s00190-019-01335-w |
| [22] |
NACIRI N, BISNATH S. An uncombined triple-frequency user implementation of the decoupled clock model for PPP-AR[J]. Journal of Geodesy, 2021, 95(5): 60. DOI:10.1007/s00190-021-01510-y |
| [23] |
郭文轩, 秘金钟, 程鹏飞, 等. 星间单差精密单点定位部分模糊度固定方法[J]. 测绘科学, 2021, 46(10): 6-12. GUO Wenxuan, BEI Jinzhong, CHENG Pengfei, et al. Fixed method of PPP partial ambiguity based on single difference between satellites[J]. Science of Surveying and Mapping, 2021, 46(10): 6-12. DOI:10.16251/j.cnki.1009-2307.2021.10.002 |
| [24] |
邵凯, 易彬, 张厚喆, 等. 单星模糊度固定的整数相位钟法及在低轨卫星定轨中的应用[J]. 测绘学报, 2021, 50(4): 487-495. SHAO Kai, YI Bin, ZHANG Houzhe, et al. Integer phase clock method with single-satellite ambiguity fixing and its application in LEO satellite orbit determination[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(4): 487-495. DOI:10.11947/j.AGCS.2021.20200302 |
| [25] |
杜祯强, 柴洪洲, 潘宗鹏, 等. 针对消电离层组合FCB的非组合PPP部分模糊度固定方法[J]. 武汉大学学报(信息科学版), 2021, 46(6): 913-919. DU Zhenqiang, CHAI Hongzhou, PAN Zongpeng, et al. Partial ambiguity resolution method for uncombined PPP using ionosphere-free combined FCB[J]. Geomatics and Information Science of Wuhan University, 2021, 46(6): 913-919. DOI:10.13203/j.whugis20190272 |
| [26] |
LIU Shuai, YUAN Yunbin. A method to accelerate the convergence of satellite clock offset estimation considering the time-varying code biases[J]. Remote Sensing, 2021, 13(14): 2714. DOI:10.3390/rs13142714 |
| [27] |
ZHANG Baocheng, ZHAO Chuanbao, ODOLINSKI R, et al. Functional model modification of precise point positioning considering the time-varying code biases of a receiver[J]. Satellite Navigation, 2021, 2(1): 11. DOI:10.1186/s43020-021-00040-4 |
| [28] |
MELBOURNE W G. The case for ranging in GPS-based geodetic systems[C]//Proceedings of the 1st International Symposium on Precise Positioning with the Global Positioning System. Rockville, MD, USA: U.S. Department of Commerce, 1985: 373-386.
|
| [29] |
WVBBENA G. Software developments for geodetic positioning with GPS using TI 4100 code and carrier measurements[C]//Proceedings of the 1st International Symposium on Precise Positioning with the Global Positioning System. Rockville, MD, USA: U.S. Department of Commerce, 1985: 403-412.
|
| [30] |
柴大帅, 卢秀山, 王胜利, 等. 信噪比的GNSS宽巷模糊度单历元固定算法[J]. 测绘科学, 2018, 43(2): 10-15. CHAI Dashuai, LU Xiushan, WANG Shengli, et al. An algorithm of GNSS wide-lane ambiguity resolution on single epoch with SNR[J]. Science of Surveying and Mapping, 2018, 43(2): 10-15. DOI:10.16251/j.cnki.1009-2307.2018.02.003 |
| [31] |
章浙涛, 李博峰, 何秀凤. 北斗三号多频相位模糊度无几何单历元固定方法[J]. 测绘学报, 2020, 49(9): 1139-1148. ZHANG Zhetao, LI Bofeng, HE Xiufeng. Geometry-free single-epoch resolution of BDS-3 multi-frequency carrier ambiguities[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(9): 1139-1148. DOI:10.11947/j.AGCS.2020.20200325 |
| [32] |
LANNES A, PRIEUR J L. Calibration of the clock-phase biases of GNSS networks: the closure-ambiguity approach[J]. Journal of Geodesy, 2013, 87(8): 709-731. DOI:10.1007/s00190-013-0641-4 |
| [33] |
张宝成, 欧吉坤, 袁运斌. 精选基准消秩亏的GNSS参考网数据处理方法[J]. 测绘学报, 2014, 43(9): 895-901. ZHANG Baocheng, OU Jikun, YUAN Yunbin. Method of processing GNSS reference network data with refined datum definition for rank-deficiency elimination[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(9): 895-901. DOI:10.13485/j.cnki.11-2089.2014.0164 |
| [34] |
SAASTAMOINEN J. Contributions to the theory of atmospheric refraction[J]. Bulletin Géodésique (1946-1975), 1972, 105(1): 279-298. DOI:10.1007/BF02521844 |
| [35] |
TEUNISSEN P J G. Success probability of integer GPS ambiguity rounding and bootstrapping[J]. Journal of Geodesy, 1998, 72(10): 606-612. DOI:10.1007/s001900050199 |
| [36] |
TEUNISSEN P J G. The least-squares ambiguity decorrelation adjustment: a method for fast GPS integer ambiguity estimation[J]. Journal of Geodesy, 1995, 70(1-2): 65-82. DOI:10.1007/BF00863419 |
| [37] |
CHANG X W, YANG X, ZHOU T. MLAMBDA: a modified LAMBDA method for integer least-squares estimation[J]. Journal of Geodesy, 2005, 79(9): 552-565. DOI:10.1007/s00190-005-0004-x |
| [38] |
TEUNISSEN P J G, VERHAGEN S. The GNSS ambiguity ratio-test revisited: a better way of using it[J]. Survey Review, 2009, 41(312): 138-151. DOI:10.1179/003962609X390058 |


