北斗卫星导航系统是由我国自主建设运行的卫星导航系统,是为全球用户提供全天候、全天时、高精度的定位、导航和授时(PNT)服务的国家重要空间基础设施[1]。北斗三号全球卫星导航系统(BDS-3)已于2020年7月正式开通[2],目前BDS-3星座包括3颗地球静止轨道(geostationary earth orbit,GEO)卫星、3颗倾斜轨道(inclined geosynchronous orbit,IGSO)卫星及24颗中地球轨道(medium earth orbit,MEO)卫星。其中,24颗MEO卫星分别由中国空间技术研究院(China Academy of Space Technology,CAST)及上海微小卫星工程中心(Shanghai Engineering Center for Microsatellites,SECM)研制[3-4]。
高精度卫星轨道产品是BDS-3精密服务的基础。太阳光压摄动作为导航卫星受到的最主要的非保守力,其精确建模是提升导航卫星轨道精度的关键。太阳光压加速度和卫星的几何构型、姿态、质量、卫星表面光学属性等参数密切相关,文献[5]建立了这些参数和光压加速度之间的物理模型。然而,由于卫星表面光学参数不准确、卫星姿态控制模型存在误差等原因,纯粹依据物理原理建立的分析型光压模型精度有限,难以取得厘米级精度的定轨结果[6-7]。不同于分析型模型,经验型模型无须考虑太阳光压力对卫星的物理作用方式,而是使用实际卫星观测数据估计光压参数,模型精度较高,因此得到了广泛应用[8]。其中,ECOM(extended code orbit model)模型[9-10]和ECOM2(the updated ECOM)模型[11-12]作为两种常用的经验型光压模型,被大多数IGS(International GNSS Service)分析中心用于GPS卫星和GLONASS卫星精密轨道产品生成[13]。同时,这两种模型也同样被普遍应用于BDS-3卫星精密定轨[14-17]。
然而,ECOM模型和ECOM2模型均非针对BDS-3卫星提出,它们在BDS-3卫星定轨中仍有一定局限。本文首先对两种经验模型在BDS-3卫星定轨中的适用性进行了分析。在此基础上,针对五参数ECOM模型在低太阳高度角时期轨道不连续性增大、ECOM2模型部分参数高度相关等问题,本文提出了不同的改进方法并通过重叠轨道比较和卫星激光测距(satellite laser ranging,SLR)检核两种方式进行模型验证。
1 BDS-3卫星经验型光压模型适用性分析ECOM模型和ECOM2模型是导航卫星精密定轨中被广泛采用的两类经验型太阳光压模型。完整的ECOM模型包含9个参数,文献[10]指出仅采用其中的D0、Y0、B0、Bc和Bs 5个参数也能得到良好的定轨结果,因此五参数ECOM模型被普遍应用。随着导航卫星系统的发展,针对GPS卫星提出的ECOM模型并不适用于其他导航卫星。为此,欧洲定轨中心提出了ECOM2模型,文献[12]指出相较ECOM模型,ECOM2模型可以明显提升GLONASS卫星、Galileo卫星和QZSS(quasi zenith satellite system)卫星的定轨精度。本节主要围绕五参数ECOM模型和ECOM2模型这两种经验光压模型在BDS-3卫星精密定轨中的适用性进行分析。重点介绍了BDS-3卫星定轨采用的策略,分析了两种光压模型的光压参数。
1.1 定轨策略本文利用全球分布的138个IGS多系统测站和26个iGMAS(international GNSS monitoring and assessment system)测站2020年的观测数据对BDS-3卫星进行精密定轨。图 1展示了这164个测站的全球分布情况,三角形为IGS多系统测站,圆点为iGMAS测站。

|
| 图 1 测站全球分布 Fig. 1 Global distributed stations |
本文使用GREAT(GNSS+research, application and teaching)[18]软件完成BDS-3卫星轨道解算。在解算过程中,选用B1I和B3I频段的BDS-3卫星观测数据组成无电离层组合消除一阶电离层误差。定轨过程中所有测站坐标均固定,不参与参数估计。其中IGS测站固定为IGS周解坐标,iGMAS测站坐标固定为单GPS精密单点定位获得的周解测站坐标。为了进一步提升轨道精度,联合GPS卫星观测数据进行BDS-3/GPS联合精密定轨解算,以增强对流层、地球自转参数等公共参数的解算可靠性。其中,GPS卫星均采用五参数ECOM光压模型。精密定轨处理中所采用的观测模型、动力学模型和参数估计策略详见表 1,不同定轨策略中仅有BDS-3卫星采用的光压模型不同。
1.2 光压模型适用性分析
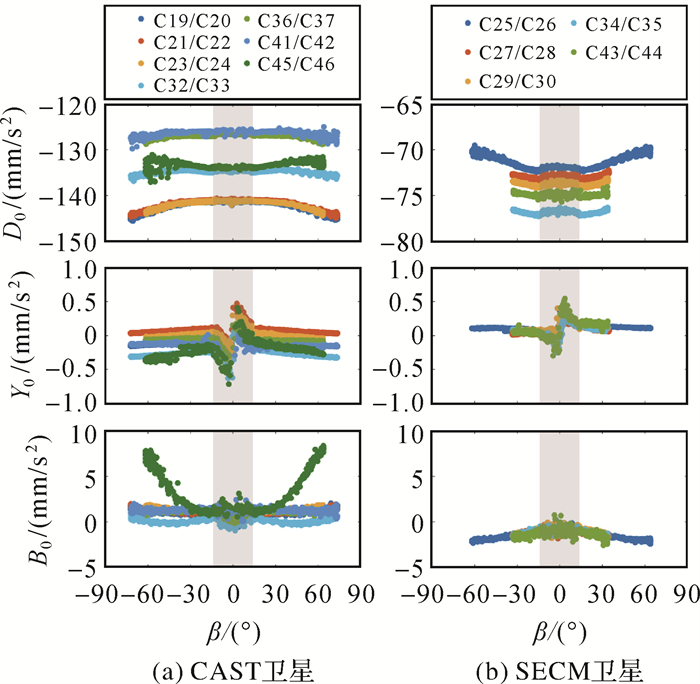
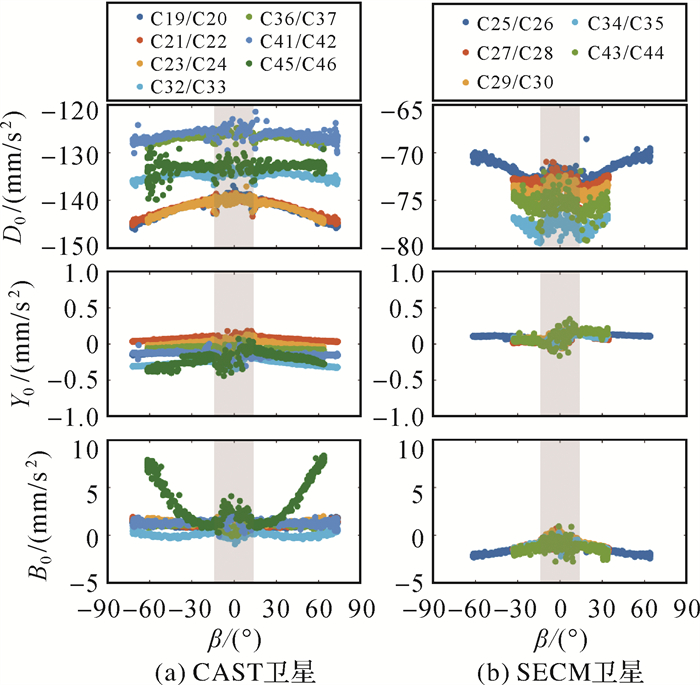
图 2和图 3分别展示了BDS-3卫星五参数ECOM模型和九参数ECOM2模型光压参数随太阳高度角(β角)的变化情况。由于BDS-3 MEO卫星均为“一箭双星”方式发射入轨,“双星”的结构、质量等都十分相近,故其光压参数估值差异小于1 nm/s2。因此,图中仅绘制了“双星”中的一颗卫星的光压参数变化情况。
|
| 图 2 CAST卫星及SECM卫星五参数ECOM模型光压参数D0、Y0、B0随太阳高度角变化(阴影区域表示地影期) Fig. 2 D0, Y0, B0 estimates from the five-parameter ECOM model for CAST and SECM satellites (The shaded areas are the eclipse periods) |
|
| 图 3 CAST卫星及SECM卫星九参数ECOM2模型光压参数D0、Y0、B0随太阳高度角变化(阴影区域表示地影期) Fig. 3 D0、Y0、B0 estimates from the nine-parameter ECOM2 model for CAST and SECM satellites (The shaded areas are the eclipse periods) |
对于D0参数,CAST卫星和SECM卫星之间有明显的区别。以五参数ECOM模型为例,CAST卫星变化范围在-146~-125 nm/s2,而SECM卫星D0参数值大小仅为-77~-69 nm/s2。这主要是由于SECM卫星的太阳能帆板面积(10.8 m2)远小于CAST卫星(20.44 m2)。对于同属CAST或SECM的卫星,D0参数大小与其卫星质量(表 2)相关,卫星质量越大,D0参数值越小。然而,C34/C35的D0参数在SECM-A卫星中最大,但其质量也最大,这说明C34/C35卫星的实际质量小于官方发布的标称值。观察ECOM2模型D0参数变化,也可得到相同的结论。此外,与五参数ECOM模型相比,ECOM2模型每颗卫星的D0分布更加离散,这可能是由于ECOM2模型在D方向存在过度参数化。
| 卫星类型 | PRN | 标称质量/kg |
| CAST MEO | C19, C20, C21 C22, C23, C24 |
941~946 |
| C32, C33 | 1007 | |
| C36, C37, C41 C42, C45, C46 |
1058~1061 | |
| SECM-A MEO | C25, C26, | 1041~1044 |
| C27, C28, C29, C30 | 1008~1018 | |
| C34, C35 | 1045~1046 | |
| SECM-B MEO | C43, C44 | 1075~1078 |
ECOM模型Y0参数在非地影期较为稳定,但在地影期内变化最大可达1.0 nm/s2,其原因可能是五参数ECOM模型不能补偿地影期内未模型化的力(如热辐射)[23]。当采用ECOM2模型时,该差异明显减小,这是由于ECOM2模型D方向的高阶周期项可以吸收这部分未模型化的误差。此外,各CAST卫星非地影期的Y0参数值差异明显,这可能是由于各卫星Y轴偏差不同引起的[24]。
对于B0参数,大部分CAST卫星的值在-1.0~2.0 nm/s2。但C45/C46两颗卫星的B0参数值最大可达到8.0 nm/s2,远大于其他CAST卫星,且与β角存在明显相关性。这说明C45/C46很可能存在和其他CAST卫星不同的卫星构型。
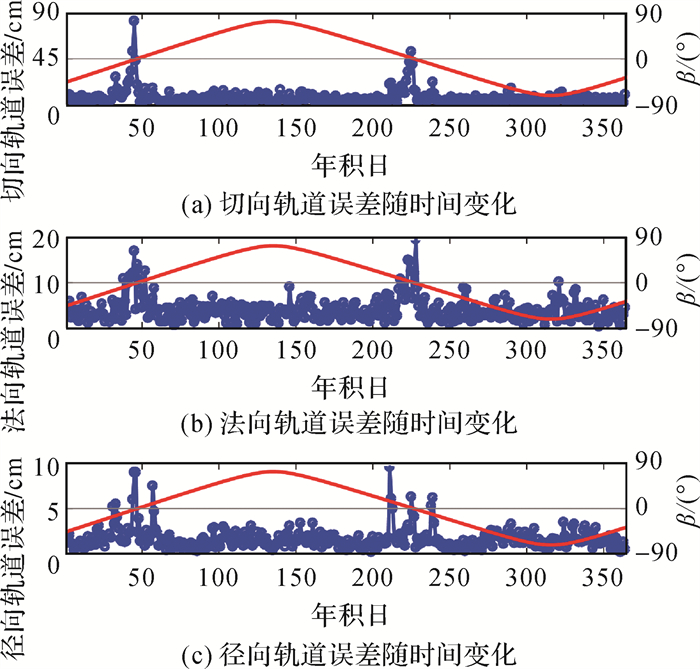
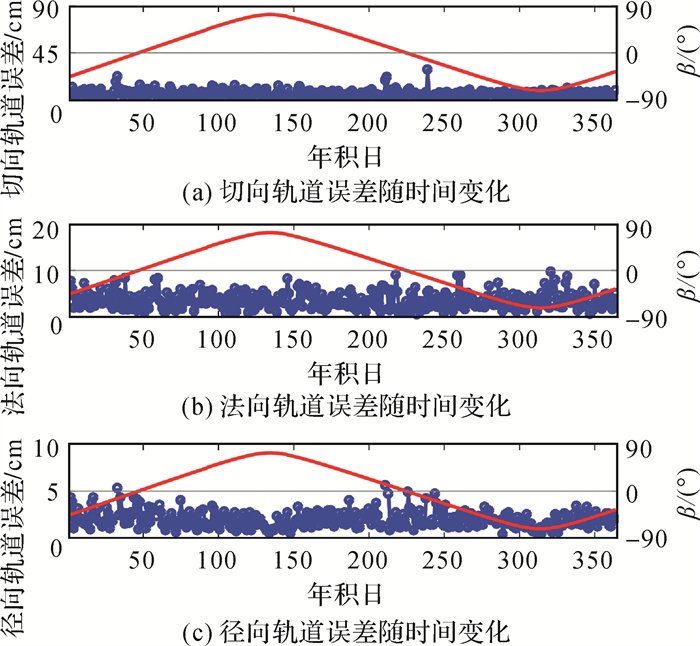
本文进一步对BDS-3卫星重叠轨道结果进行了分析,示例性选取其中一颗卫星(C20)进行分析,其余CAST卫星与C20表现相近。图 4和图 5分别展示了采用五参数ECOM模型和九参数ECOM2模型的C20的重叠轨道误差随时间变化序列。可以发现,在低太阳高度角时期,采用ECOM模型,卫星轨道不连续性明显增大,切向误差最大可上升至78 cm。SECM卫星结果表明,在低太阳高度角时期卫星轨道不连续性同样增大,但幅度小于CAST卫星(切向误差上升28%左右)。而采用ECOM2模型后,低太阳高度角时期的重叠轨道误差并没有明显上升。这进一步表明五参数ECOM模型在低太阳高度角时期不适用于BDS-3卫星精密定轨。
|
| 图 4 五参数ECOM模型C20(CAST)重叠轨道误差随时间变化(红线表示β角) Fig. 4 Overlapping results of the five-parameter ECOM model for C20 (CAST) (the red lines are the β angles) |
|
| 图 5 九参数ECOM2模型C20(CAST)重叠轨道误差随时间变化(红线表示β角) Fig. 5 Overlapping results of the nine-parameter ECOM2 model for C20 (CAST) (the red lines are the β angles) |
此外,针对ECOM2模型D0参数分布离散的现象,本文进一步分析了ECOM2模型各个光压参数之间的相关性,分别选取了一颗CAST(C19)、一颗SECM(C25)卫星作为代表进行分析,其余卫星表现类似。图 6展示了C19和C25在β角为25°时各个ECOM2参数之间的相关系数。由图 6可知,D0和D2c之间,D2s和Bs之间存在明显的强相关性。图 7进一步展示了D0和D方向各周期项参数及D2s和Bs之间的相关关系。可以发现,D0和D2c之间的相关性明显和β角相关。当β角在30°以内时,D0和D2c之间的相关系数约为1,但随着β角增大,相关系数急速下降。D2s和Bs的相关系数值则均在0.94以上,这表明D2s和Bs参数一直具有强相关性。
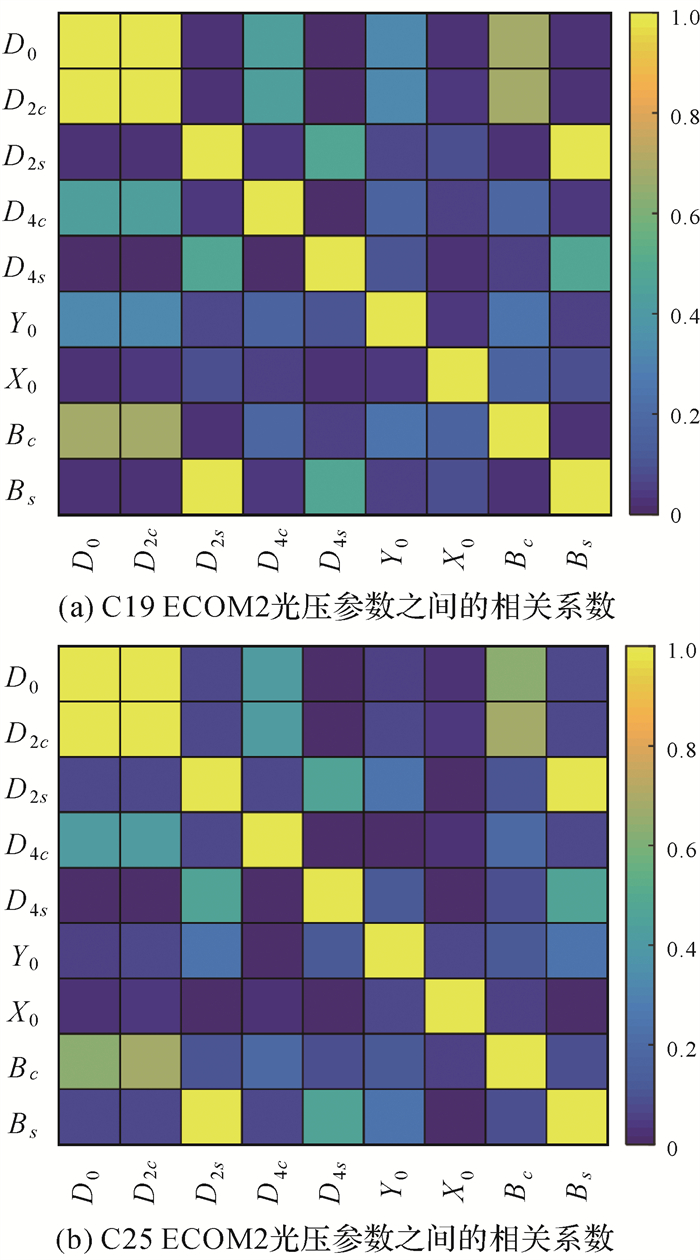
|
| 图 6 C19和C25 ECOM2光压参数之间的相关系数 Fig. 6 correlation coefficients between the ECOM2 SRP parameters for C19 and C25 |
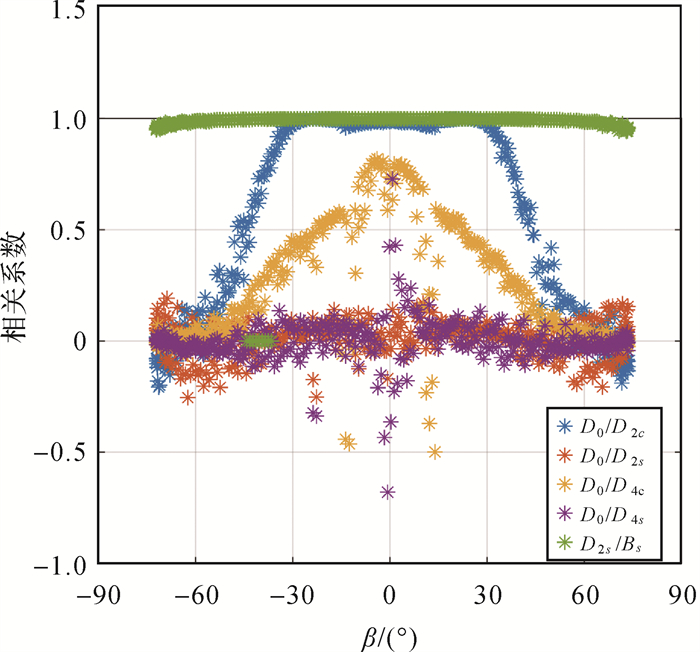
|
| 图 7 九参数ECOM2模型光压参数相关系数随太阳高度角变化 Fig. 7 Correlation coefficients of nine-parameter ECOM2 model as a function of β angle |
2 经验光压模型改进方法
如1.2节所述,五参数ECOM模型和ECOM2模型在BDS-3卫星定轨中均存在一定的问题,这两个模型并不完全适用于BDS-3卫星定轨。五参数ECOM模型在太阳高度角较低时,呈现出明显的轨道不连续性,这是由于BDS-3卫星的长方体构型导致的。当太阳高度角较大时,卫星+X面受照,光压摄动在轨道运行周期内变化较小;当太阳高度角较小时,卫星+X、+Z和-Z面轮流受照,由于X面于Z面面积不同,光压摄动随轨道运行周期呈现明显周期性变化,D0常量参数无法吸收该周期误差。基于此,本文提出了在五参数ECOM模型的D方向引入周期项以降低BDS-3卫星在太阳高度角较低时的轨道不连续性。同时为了探究不同周期项对BDS-3卫星定轨的影响并尽可能减少光压参数,对引入不同周期项的定轨结果进行分析。对于ECOM2模型,其D0参数分布更为离散,这可能是因为ECOM2模型在D方向存在过度参数化。通过对ECOM2模型参数之间相关性的分析,发现D0和D2c之间、D2s和Bs之间存在强相关性。考虑到该相关性,本文提出通过减少ECOM2模型二阶周期项以进一步提高轨道精度。综上所述,本文主要的改进方法如下:
(1) 针对五参数ECOM模型低β角时期轨道不连续性增大的问题,在五参数ECOM模型的D方向引入了一阶周期项。分别对只引入Dc周期项(ECOM_Dc)、只引入Ds周期项(ECOM_ Ds)及同时引入Dc和Ds周期项(ECOM_DcDs)的情况进行分析。
(2) 针对ECOM2模型中部分参数间存在的强相关性,分析了不估计D2c的八参数ECOM2模型(8ECOM2),以及不估计D2c和D2s的七参数ECOM2模型(7ECOM2)的定轨精度。
表 3给出了上述改进模型的光压参数列表。作为对比,五参数ECOM模型与九参数ECOM2模型也同时给出。
| 模型 | 光压参数列表 |
| ECOM | D0, Y0, B0, Bc, Bs |
| ECOM_Dc | D0, Dc, Y0, B0, Bc, Bs |
| ECOM_Ds | D0, Ds, Y0, B0, Bc, Bs |
| ECOM_DcDs | D0, Dc, Ds, Y0, B0, Bc, Bs |
| ECOM2 | D0, D2c, D2s, D4c, D4s, Y0, B0, Bc, Bs |
| 8ECOM2 | D0, D2s, D4c, D4s, Y0, B0, Bc, Bs |
| 7ECOM2 | D0, D4c, D4s, Y0, B0, Bc, Bs |
3 结果分析 3.1 重叠轨道结果
重叠轨道比较是评估卫星轨道内符合精度的常用方法,本文选取了24 h弧长的重叠轨道用于计算重叠轨道精度。
图 8展示了在2020年DOY 211—DOY 238期间β角小于14°的C19、C20、C21、C22、C32及C33卫星(由于C41/C42卫星观测数据较少,定轨精度和其他卫星存在差距,因此C41/C42未计入统计)重叠轨道误差统计结果。由图 8可知,在D方向引入周期项可以明显减小重叠轨道误差值,其中轨道切向改善最为明显。与五参数ECOM模型相比,ECOM_Ds模型将切向、法向、径向重叠轨道误差分别从13.6、6.6、2.4 cm减小到6.6、4.6、1.7 cm;ECOM_Dc模型在切向和法向的改进更明显,其重叠轨道误差分别为5.4、3.2、1.7 cm;ECOM_DcDs模型在切向和法向上有所提升,但径向精度却有所下降,重叠轨道误差值分别为7.5、4.9、3.8 cm。总体而言,在D方向引入周期项可以减小约36.4%~57.5%的一维重叠误差。在D方向引入一阶周期项Dc的改善结果最明显,可以达到与非低β角期间的卫星重叠轨道精度相当的水平。对于SECM卫星,本文选择了2020年DOY 270—DOY 305期间的地影期卫星进行结果统计(见表 4,由于观测数据较少,C43/C44未计入统计)。相较CAST卫星,SECM卫星在低β角时期重叠轨道精度降低不明显(一维重叠精度下降约26.7%),在D方向引入周期项Dc或同时引入Dc和Ds可将SECM卫星低β角时期重叠轨道精度提升至和非低β角时期精度相当的水平,但引入Ds周期项反而降低了重叠轨道精度(一维重叠精度下降约38.6%)。
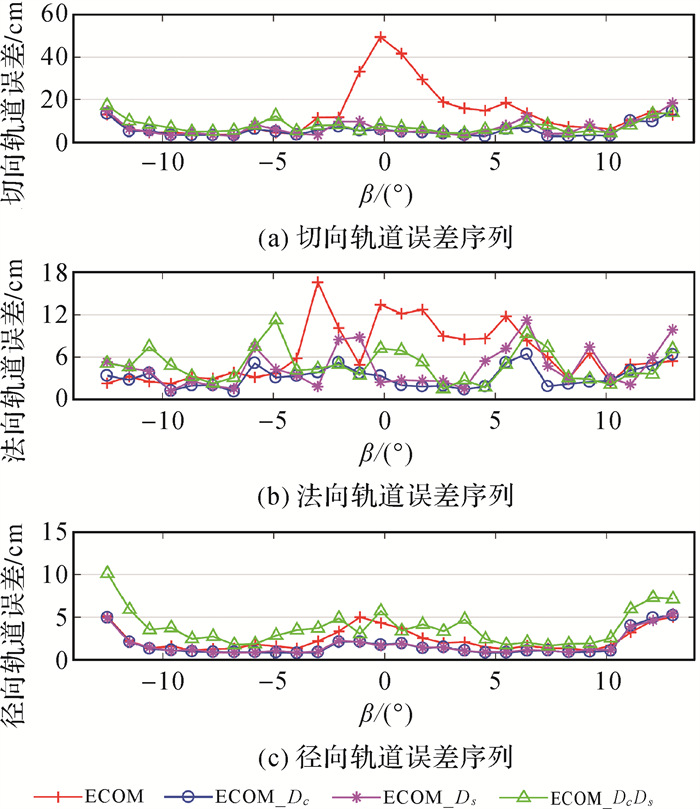
|
| 图 8 不同ECOM模型在低太阳高度角时期重叠轨道误差序列结果 Fig. 8 Overlapping results for different ECOM models during low β angle |
| 卫星 | ECOM | ECOM_Dc | ECOM_Ds | ECOM_DcDs | |||||||||||
| 切向 | 法向 | 径向 | 切向 | 法向 | 径向 | 切向 | 法向 | 径向 | 切向 | 法向 | 径向 | ||||
| CAST | 13.6 | 6.6 | 2.4 | 5.4 | 3.2 | 1.7 | 6.6 | 4.6 | 1.7 | 7.5 | 4.9 | 3.8 | |||
| SECM | 6.9 | 4.5 | 1.5 | 5.0 | 3.2 | 1.2 | 8.9 | 7.3 | 1.5 | 5.1 | 2.5 | 2.1 | |||
图 9展示了ECOM2模型、8ECOM2模型及7ECOM2模型的非地影期重叠轨道误差统计结果。需要指出的是,由于2颗SECM卫星(C43/C44,SECM-B)及4颗CAST卫星(C41/C42/C45/C46)发射于2019年下半年,其观测数据仍然较少,此外C45/C46卫星构型有别于其他CAST卫星。因此,本文单独统计了这些卫星的重叠轨道误差。结果表明,8ECOM2模型可以明显降低卫星重叠轨道误差。与ECOM2模型相比,8ECOM2模型能够将CAST卫星和SECM卫星一维重叠轨道误差从3.8 cm和4.2 cm减小到3.6 cm和3.9 cm(对于C41/C42、C45/C46和C43/C44则分别从6.1、8.2和7.2 cm减小为5.9、7.6和6.7 cm)。且在切向、法向、径向3个方向中,8ECOM2模型对轨道径向精度的提升最为明显,可达到17.4%~28.6%。7ECOM2模型可在8ECOM2模型基础上进一步提升卫星重叠轨道精度,径向误差进一步减小了5.2%~8.5%。此外,对低太阳高度角时期的ECOM2模型、8ECOM2模型及7ECOM2模型重叠轨道结果进行统计。结果显示相较ECOM2模型,8ECOM2模型及7ECOM2模型均对径向重叠轨道提升明显,其中8ECOM2模型可将CAST及SECM卫星径向误差分别从2.7 cm和2.5 cm减小为2.3 cm和1.8 cm;7ECOM2模型则分别减小到2.0 cm和1.6 cm。
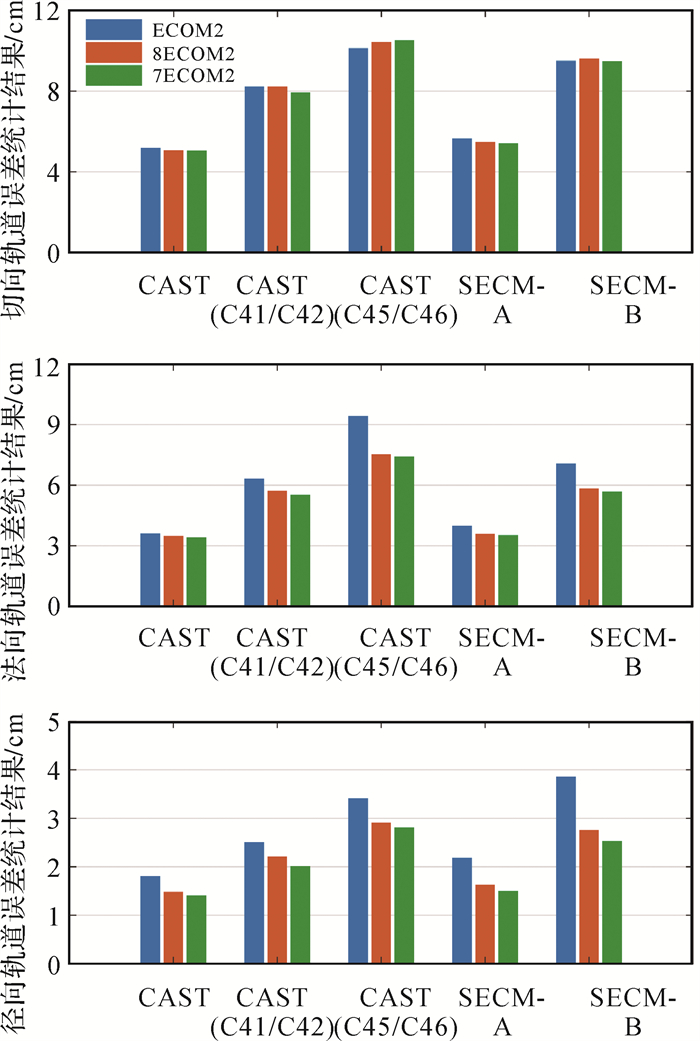
|
| 图 9 不同ECOM2模型重叠轨道误差统计 Fig. 9 Overlapping results of different ECOM2 models |
表 5统计了非地影时期的五参数ECOM模型、九参数ECOM2模型、8ECOM2模型及7ECOM2模型在卫星切向、法向、径向的重叠轨道误差统计结果。整体而言,五参数ECOM模型的重叠轨道误差小于ECOM2模型。但通过对ECOM2模型光压参数的重新选取,对于不估计D2c和D2s的七参数ECOM2模型,其SECM卫星定轨精度和五参数ECOM模型相当,CAST卫星精度则更优。
| 卫星 | ECOM | ECOM2 | 8ECOM2 | 7ECOM2 | |||||||||||
| 切向 | 法向 | 径向 | 切向 | 法向 | 径向 | 切向 | 法向 | 径向 | 切向 | 法向 | 径向 | ||||
| CAST MEO | 5.8 | 3.4 | 1.8 | 5.2 | 3.6 | 1.8 | 5.0 | 3.5 | 1.5 | 5.0 | 3.4 | 1.4 | |||
| CAST MEO (C41/C42) |
8.1 | 5.3 | 2.2 | 8.2 | 6.3 | 2.5 | 8.2 | 5.7 | 2.2 | 7.9 | 5.5 | 2.0 | |||
| CAST MEO (C45/C46) |
10.4 | 7.2 | 2.9 | 10.1 | 9.4 | 3.4 | 10.4 | 7.5 | 2.9 | 10.5 | 7.4 | 2.8 | |||
| SECM-A | 5.4 | 3.5 | 1.5 | 5.6 | 4.0 | 2.2 | 5.5 | 3.6 | 1.6 | 5.4 | 3.5 | 1.5 | |||
| SECM-B | 9.5 | 5.7 | 2.4 | 9.5 | 7.0 | 3.9 | 9.5 | 5.7 | 2.8 | 9.5 | 5.7 | 2.5 | |||
3.2 SLR检核
除重叠轨道误差外,本文还采用SLR检核的方法对BDS-3卫星轨道精度进行评价。SLR作为独立的轨道径向精度评价方式被广泛应用于卫星轨道外符合精度评定。目前所有BDS-3卫星均搭载了激光反射棱镜,其中4颗卫星(C20/C21/C29/C30)被国际激光测距服务组织(international laser ranging service, ILRS)持续观测[25]。需要指出的是,本文选取了3 d定轨弧段的中间24 h用于SLR检核,并将绝对值大于50 cm的残差作为粗差剔除。
同样选取了2020年DOY 211—DOY 238和DOY 270—DOY 305之间的观测数据,对改进后的五参数ECOM模型进行SLR检核验证。表 6展示了低太阳高度角时期的4颗卫星C20、C21、C29、C30采用五参数ECOM模型,ECOM_Dc模型、ECOM_Ds模型及ECOM_DcDs模型的SLR残差统计结果。与五参数ECOM模型相比,在D方向只引入一项周期项,CAST卫星的SLR残差的平均偏差减小了0.2~0.6 cm,标准差略有增大,SECM卫星SLR残差的标准差减小约0.2 cm;在D方向同时引入周期项Dc和Ds,SLR残差平均偏差和标准差均有不同程度增大。
| PRN | #NP | ECOM | ECOM_Dc | ECOM_Ds | ECOM_DcDs | |||||||
| 平均值 | 标准差 | 平均值 | 标准差 | 平均值 | 标准差 | 平均值 | 标准差 | |||||
| CAST C20 | 265 | 3.4 | 3.5 | 3.2 | 3.5 | 2.8 | 3.5 | 7.4 | 4.4 | |||
| CAST C21 | 221 | 3.6 | 4.4 | 3.4 | 4.9 | 3.0 | 4.9 | 7.0 | 5.3 | |||
| SECM C29 | 169 | -4.8 | 3.3 | -4.6 | 3.1 | -4.8 | 3.3 | -4.8 | 3.8 | |||
| SECM C30 | 184 | -5.0 | 3.5 | -5.1 | 3.3 | -5.5 | 3.4 | -5.2 | 3.6 | |||
表 7统计了非地影期的五参数ECOM模型、ECOM2模型、8ECOM2模型以及7ECOM2模型SLR残差统计结果。可以看到,所有模型SLR残差的平均偏差与标准差都在5.0 cm以内。相较五参数ECOM模型,九参数ECOM2模型平均偏差减小了0.5~1.0 cm,标准差减小了0.1~0.4 cm。相较九参数ECOM2模型,不估计D2c和D2s参数后,SECM卫星的SLR残差的平均偏差及标准差均增大,其精度和五参数ECOM模型相当;CAST卫星平均偏差增大,但其标准差有所下降。这可能是由于未被吸收的地球反照辐射、天线推力等动力学误差导致的。表 8统计了地影期不同参数ECOM2模型的SLR检核结果。结果显示采用7ECOM2模型可以一定程度上降低地影期的SLR残差的标准差,对于SECM卫星标准差降幅可达1.1~1.2 cm。这主要是因为在低太阳高度角时期光压参数均高度相关,减少估计参数更有利于轨道解算。
| PRN | #NP | ECOM | ECOM2 | 8ECOM2 | 7ECOM2 | |||||||
| 平均值 | 标准差 | 平均值 | 标准差 | 平均值 | 标准差 | 平均值 | 标准差 | |||||
| CAST C20 | 3245 | 4.8 | 3.3 | 4.3 | 3.2 | 4.8 | 3.3 | 4.8 | 3.1 | |||
| CAST C21 | 3407 | 4.8 | 3.5 | 4.3 | 3.3 | 4.9 | 3.3 | 4.9 | 3.2 | |||
| SECM C29 | 2216 | -4.6 | 4.7 | -3.7 | 4.3 | -4.5 | 4.9 | -4.6 | 4.7 | |||
| SECM C30 | 2117 | -4.9 | 4.4 | -3.9 | 4.0 | -4.9 | 4.6 | -5.0 | 4.4 | |||
| PRN | #NP | ECOM2 | 8ECOM2 | 7ECOM2 | |||||
| 平均值 | 标准差 | 平均值 | 标准差 | 平均值 | 标准差 | ||||
| CAST C20 | 265 | 2.2 | 3.4 | 0.7 | 3.7 | 2.5 | 3.2 | ||
| CAST C21 | 221 | 2.8 | 3.4 | 2.1 | 4.4 | 3.3 | 3.7 | ||
| SECM C29 | 169 | -2.5 | 4.3 | -2.6 | 4.2 | -3.7 | 3.2 | ||
| SECM C30 | 184 | -3.6 | 4.5 | -3.5 | 4.0 | -4.7 | 3.3 | ||
4 总结
本文利用2020年观测数据,对ECOM、ECOM2这两类常用的经验型太阳光压模型在BDS-3精密定轨中的适用性进行分析。针对两种模型在BDS-3定轨中存在的缺陷,分别提出了相应改进策略,并通过重叠轨道比较和SLR检核两种方式进行模型验证。主要结论有:
(1) C45和C46两颗卫星的B0参数远大于其他卫星,且和β角呈现出明显相关性,这可能是由于C45和C46存在不同于其他CAST卫星的卫星构型;C34和C35两颗卫星的D0值大于其他SECM-A卫星,而其质量也为最大,说明这两颗卫星实际质量小于其标称值。
(2) 针对五参数ECOM模型在低β角时轨道不连续性明显增大的问题,采用在D方向增加周期项参数的方式进行改进。结果表明,在D方向增加周期项Dc参数对重叠轨道误差改善最为明显。相较五参数ECOM模型,加入Dc周期项后,CAST卫星重叠轨道径向、法向、切向误差分别减少了60.3%、51.5%、29.2%。因此,当在地影期采用ECOM模型时,应在五参数ECOM模型的基础上额外引入一阶周期项Dc。
(3) ECOM2模型参数之间的相关系数表明D0和D2c之间、D2s和Bs之间存在强相关性。将D2c参数移除后,和ECOM2模型相比,重叠轨道径向精度可提升0.3~1.1 cm;在此基础上将D2s移除后,径向精度可进一步提升0.1~0.3 cm。CAST卫星SLR残差标准差减小,SECM卫星增大;两类卫星的SLR平均偏差均有所增大。
(4) 对于CAST卫星,不估计D2c和D2s的七参数ECOM2模型可以得到最小的重叠轨道误差和SLR残差标准差;对于SECM卫星,七参数ECOM2模型的精度和五参数ECOM模型相当。综合考虑重叠轨道精度和SLR检核精度,七参数ECOM2模型更适于BDS-3卫星精密定轨。
致谢: 本文的数值计算得到了武汉大学超级计算中心的支持和帮助。
| [1] |
中华人民共和国国务院新闻办公室. 中国北斗卫星导航系统白皮书[M]. 北京: 人民出版社, 2016. The State Council Information Office of the People's Republic of China. China BeiDou satellite navigation system[M]. Beijing: People's Publishing House, 2016. |
| [2] |
蔡洪亮, 孟轶男, 耿长江, 等. 北斗三号全球导航卫星系统服务性能评估: 定位导航授时、星基增强、精密单点定位、短报文通信与国际搜救[J]. 测绘学报, 2021, 50(4): 427-435. CAI Hongliang, MENG Yinan, GENG Changjiang, et al. BDS-3 performance assessment: PNT, SBAS, PPP, SMC and SAR[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(4): 427-435. DOI:10.11947/j.AGCS.2021.20200549 |
| [3] |
中国卫星导航系统管理办公室. 北斗卫星参数文件[EB/OL]. [2021-10-16]. http://www.beidou.gov.cn/yw/gfgg/201912/W020200323534413073762.zip. China Satellite Navigation Office. Satellite information of BDS[EB/OL]. [2021-10-16]. http://www.beidou.gov.cn/yw/gfgg/201912/W020200323534413073762.zip. |
| [4] |
LI Xingxing, YUAN Yongqiang, ZHU Yiting, et al. Improving BDS-3 precise orbit determination for medium earth orbit satellites[J]. GPS Solutions, 2020, 24(2). DOI:10.1007/s10291-020-0967-3 |
| [5] |
MILANI A, NOBILI AM, FARINELLA P. Non-gravitational perturbations and satellite geodesy[M]. Bristol, UK: Adam Hilger, 1987.
|
| [6] |
GUO Jing, CHEN Guo, ZHAO Qile, et al. Comparison of solar radiation pressure models for BDS IGSO and MEO satellites with emphasis on improving orbit quality[J]. GPS Solutions, 2017, 21(2): 511-522. DOI:10.1007/s10291-016-0540-2 |
| [7] |
RODRIGUEZ-SOLANO C, HUGENTOBLER U, STEIGENBERGER P. Adjustable box-wing model for solar radiation pressure impacting GPS satellites[J]. Advances in Space Research, 2012, 49: 1113-1128. DOI:10.1016/j.asr.2012.01.016 |
| [8] |
王晨. 北斗导航卫星光压模型构建与精化研究[D]. 武汉: 武汉大学, 2019. WANG Chen. Solar radiation pressure modelling for BeiDou navigation satellites[D]. Wuhan: Wuhan University, 2019. |
| [9] |
BEUTLER G, BROCKMANN E, GURTNER W, et al. Extended orbit modeling techniques at the CODE processing center of the international GPS service for geodynamics (IGS): theory and initial results[J]. Manuscripta Geodaetica, 1994, 19(6): 367-386. DOI:10.1183/09031936.94.07071350 |
| [10] |
SPRINGER TA, BEUTLER G, ROTHACHER M. Improving the orbit estimates of GPS satellites[J]. Journal of Geodesy, 1999, 73(3): 147-157. DOI:10.1007/s001900050230 |
| [11] |
ARNOLD D, MEINDL M, BEUTLER G, et al. CODE's new solar radiation pressure model for GNSS orbit determination[J]. Journal of Geodesy, 2015, 89(8): 775-791. DOI:10.1007/s00190-015-0814-4 |
| [12] |
PRANGE L, ORLIAC E, DACH R, et al. CODE's fIve-system orbit and clock solution-the challenges of multi-GNSS data analysis[J]. Journal of Geodesy, 2017, 91(4): 345-360. DOI:10.1007/s00190-016-0968-8 |
| [13] |
MONTENBRUCK O, STEIGENBERGER P, HUGEN-TOBLER U. Enhanced solar radiation pressure modeling for Galileo satellites[J]. Journal of Geodesy, 2015, 89(3): 283-297. DOI:10.1007/s00190-014-0774-0 |
| [14] |
LI Ran, WANG Ningbo, LI Zishen, et al. Precise orbit determination of BDS-3 satellites using B1C and B2a dual-frequency measurements[J]. GPS solutions, 2021, 25(3): 95. DOI:10.1007/s10291-021-01126-x |
| [15] |
XU Xiaolong, WANG Xilong, LIU Jingnan, et al. Characteristics of BD3 global service satellites: POD, open service signal and atomic clock performance[J]. Remote Sensing, 2019, 11(13): 1559. DOI:10.3390/rs11131559 |
| [16] |
YAN Xingyuan, HUANG Guanwen, ZHANG Qin, et al. Early analysis of precise orbit and clock offset determination for the satellites of the global BeiDou-3 system[J]. Advances in Space Research, 2018, 63(3): 1270-1279. DOI:10.1016/j.asr.2018.10.038 |
| [17] |
ZHANG Bo, JIA Xiaolin, SUN Fuping, et al. Performance of BeiDou-3 satellites: signal quality analysis and precise orbit determination[J]. Advances in Space Research, 2019, 64(3): 687-695. DOI:10.1016/j.asr.2019.05.016 |
| [18] |
LI Xingxing, HAN Xinjuan, LI Xin, et al. GREAT-UPD: An open-source software for uncalibrated phase delay estimation based on multi-GNSS and multi-frequency observations[J]. GPS Solution, 2021, 25(2): 66. DOI:10.1007/s10291-020-01070-2 |
| [19] |
中国卫星导航系统管理办公室. 北斗卫星天线相位中心文件[EB/OL]. [2021-05-04]. 2019. http://www.beidou.gov.cn/yw/gfgg/201912/W020200323534413069510.atx. China Satellite Navigation Office. Satellite antenna phase center of BDS[EB/OL]. [2021-05-04]. http://www.beidou.gov.cn/yw/gfgg/201912/W020200323534413069510.atx. |
| [20] |
PAVLIS N K, HOLMES S A, KENYON S C, et al. The development and evaluation of the earth gravitational model 2008 (EGM2008)[J]. Journal of Geophysical Research: Solid Earth, 2012, 117(B4). DOI:10.1029/2011JB008916 |
| [21] |
LYARD F, LEFEVRE F, LETELLIER T, et al. Modelling the global ocean tides: modern insights from FES2004[J]. Ocean Dynamics, 2006, 56(5-6): 394-415. DOI:10.1007/s10236-006-0086-x |
| [22] |
PETIT G, LUZUM B. IERS conventions 2010[R]. Frankfurt am Main: Verlag des Bundesamts für Kartographie und Geodäsie, 2010.
|
| [23] |
DUAN Bingbing, HUGENTOBLER U, HOFACKER M, et al. Improving solar radiation pressure modeling for GLONASS satellites[J]. Journal of Geodesy, 2020, 94(8). DOI:10.1007/s00190-020-01400-9 |
| [24] |
KUANG D, RIM HJ, SCHUTZ BE, et al. Modeling GPS satellite attitude variation for precise orbit determination[J]. Journal of Geodesy, 1996, 70(9): 572-580. DOI:10.1007/BF00867865 |
| [25] |
PEARLMAN M, DEGNAN J, BOSWORTH J. The international laser ranging service[J]. Advances in Space Research, 2002, 30(2): 135-143. |





