2. 成都信息工程大学资源环境学院,四川 成都 610225
2. Faculty of Resources and Environment, Chengdu University of Information Technology, Chengdu 610225, China
高精度位置服务(location-based service,LBS) 是GNSS PNT体系的重要发展方向[1-2]。为了实现厘米级甚至毫米级的高精度位置服务,以载波实时动态差分(real time kinematic, RTK)和精密单点定位(precise point positioning, PPP)两种模式为代表,并基于地基或星基增强,形成了VRS\FKP\MAC等为代表的Network RTK和PPP-RTK等技术解决方案。PPP-RTK除了高度依赖区域地基CORS站的数量与分布外,还需要卫星轨道、精密电离层模型、高精度钟差及硬件延迟等实时产品的支持,仍处于开发和早期应用阶段[3]。相对于以虚拟参考站(virtual reference station,VRS)为代表的网络RTK技术而言,PPP-RTK的稳定性、连续性和可用性依然在发展和提升中,VRS仍然是目前最为稳定、可靠的高精度实时位置服务模式,并将在未来发展中逐步融合Network RTK和PPP-RTK,形成基于地基和星基增强的融合位置服务模式。
在“+GNSS”发展理念下,地基CORS增强系统的发展备受社会关注,覆盖全国的CORS网络正在日益完善[4-5]。虚拟参考站技术因其独特优势,在CORS网位置服务中使用最为广泛。但是VRS需要为每个流动站分配一个虚拟参考站,随着海量并发用户响应对服务器性能提出更高需求,格网化VRS技术应运而生。格网化VRS的关键是确定格网的结构和间距,目前的研究仍采用经验间距值,在一定程度上制约了用户定位精度和服务器解算效率。
广域位置服务的格网化VRS是通过虚拟格网的划分形成差分资源池[6],有学者从数学的角度分析了CORS网络和VRS的结构,但格网间距的确定不仅是数学的,更是物理的属性,它受空间大气延迟及其空间变化趋势的影响[7-9]。因此,本文针对广域网络RTK/VRS,构建格网化VRS的划分体系,并就顾及大气延迟梯度的虚拟格网划分方法及其性能进行测试。
1 广域网络RTK的VRS格网化格网化VRS是在传统VRS技术存在用户高并发限制的背景下发展而来。首先,根据CORS网络覆盖范围进行格网划分。其次,终端用户连接服务端,并向服务端发送的概略坐标,获取与其距离最小的VRS格网点的虚拟观测值,该VRS格网点的虚拟观测值将作为其有效服务距离范围内,所有流动用户在一定时间内的虚拟参考站。格网点处生成虚拟观测值的数学模型如式(1)—式(6)所示。设s为主参考站A与虚拟参考站v间的共视卫星,则伪距和相位观测值的站间单差观测方程如下
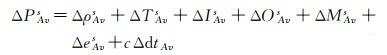 (1)
(1)
 (2)
(2)
将主参考站移至右边可得VRS观测值,同时由双差算子Δ(·)Avs=Δ▽(·)Avrs+Δ(·)Avr可得
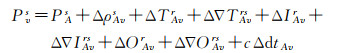 (3)
(3)
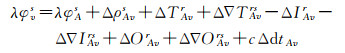 (4)
(4)
式中,ΔTAvr、ΔIAvr、ΔOAvr为常量,r卫星的高度角较大,认为其在差分计算中消除;VRS的坐标精确已知,认为其模糊度、多路径、钟差、观测噪声与主参考站一致,则可得VRS伪距和相位观测值
 (5)
(5)
 (6)
(6)
对流层延迟和电离层延迟是随时间和空间变化的,在不同的地区会呈现局部差异,格网VRS的有效服务间距受大气延迟的影响,在不同的地区或环境条件下存在时空变化特性。但VRS虚拟格网密度会影响解算服务器的负荷,尤其在局地用户并发服务申请增大的情况下,网络RTK定位服务性能会受到较大影响[10-11]。因此,有必要根据大气延迟的变化动态调整格网间距,以优化服务器解算效率,提高用户定位服务性能。
2 VRS网格的划分方法 2.1 VRS坐标格网划分VRS有效服务距离指在保障用户定位精度的情况下,流动站与VRS间的最大距离,虚拟格网间距则为其值的1.4~2倍[12-13]。相关研究表明,在CORS站网密度足够的情况下,解算单元Cell[12-16]的大气延迟变化近似线性(实际上电离层延迟的时空特性较复杂,尤其在低纬度地区或电离层较活跃的时间段,模型的性能会下降[17],这里暂不讨论),因此可以利用模型内插出流动站位置的空间大气延迟。
以内插模型为例,空间大气延迟计算如下
 (7)
(7)
式中,ΔN、ΔE是以主参考站为原点的平面坐标差;a、b为模型系数,即北、东方向上大气延迟梯度。在由基站A、B、C组成的三角网单元中,基线AB、AC之间的大气延迟满足式(7),如图 1(a)所示。

|
| 图 1 VRS坐标格网 Fig. 1 Coordinate grid VRS |
若任一流动用户Rj,VRS的最大有效服务距离为Dmax,则按方格网划分的VRS格网间距d满足:‖Vj-Rj‖≤Dmax, 则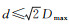
通常可不考虑大气延迟的水平方向梯度,VRS有效服务距离只与距离有关,引入最小二乘算法中系数矩阵保持不变的载波相位双差相对定位模型[18]。通过最小二乘迭代过程,系数矩阵▽B仅与参考站和卫星位置有关,因此容易得到空间大气延迟对基线向量的影响,如式(8)所示
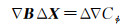 (8)
(8)
式中,ΔX= [Δx, Δy, Δz]T为空间大气延迟对基线各分量影响的误差值;Δ ▽Cϕ=Δ ▽T-Δ ▽I,为双差对流层、双差电离层对相位双差观测值的影响。若Δ ▽Cϕ已知,可通过最小二乘法求解,如式(9)所示
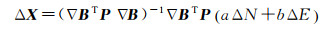 (9)
(9)
式中,P为权阵;a、b分别为南北、东西方向梯度。
考虑到网络RTK的厘米级精度,则可求得VRS有效服务的最大距离Dmax。
2.2 VRS三角形格网划分对于地形复杂的山区CORS网络,基站之间存在显著的高差,按照常规的VRS格网划分算法确定格网间距不妥[19]。顾及地形影响的VRS格网划分,需要获取地势起伏地区的数字高程模型(DEM),并利用DEM设置密度不同的插值点生成不规则三角网(triangulated irregular network,TIN),从而保证VRS格网的最优化,如图 2所示。

|
| 图 2 VRS不规则三角网生成 Fig. 2 Triangulated irregular network (TIN) VRS |
TIN生成后,在每个三角形内设置虚拟参考站,将其设置在TIN中每个三角形的坐标中心,该中心的位置可由式(10)得到
 (10)
(10)
式中,XVRS、YVRS、ZVRS分别为虚拟格网几何中心坐标值;Xi、Yi、Zi分别为虚拟格网顶点坐标值,根据图 2中矩形框区域的地形情况,建立的VRS格网如图 2(b)所示,形成格网化VRS。Si为VRS到三角形顶点的边长,使得Smax < Dmax,Dmax为设定的VRS最大服务距离(针对不同地区通过试验获得)。
3 格网化VRS的服务性能分析为了验证VRS格网方法的有效性,选择电离层活跃度较典型地区的CORS进行试验,按坐标和三角形格网确定VRS的有效服务间距,并取较短的间距作为服务性能统计指标,以降低VRS的不可用风险。
3.1 中纬度地区VRS格网化试验VRS有效服务距离的确定是以Cell为单元进行的,在不同地区的CORS网络中,各子网的大气延迟时空特性时有差异。首先以西南地区某CORS网为例,分析VRS格网有效服务的最大间距(限值),试验CORS网的Cell结构及VRS位置(ROV)如图 3所示。

|
| 图 3 中纬度地区CORS及VRS位置 Fig. 3 CORS in mid-latitude region and VRS location |
3个CORS站(SCWJ、SCXD、SCLQ)构成一个解算单元,并选择CORS站ROV(▲标注的位置)作为流动站进行RTK定位,红色圆点为选取的VRS位置。分别以ROV点平面方向1~15 km生成6个VRS,其中由近及远分别距离ROV点1、3、6、9、12和15 km。通过VRS为基准对流动站ROV进行RTK定位,将RTK定位结果与CORS站点ROV的已知坐标比较,测试并验证RTK定位精度。
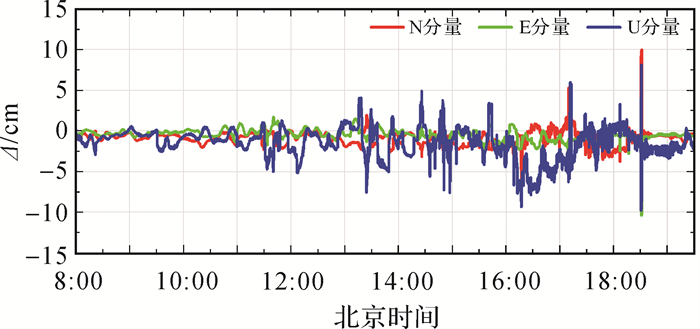
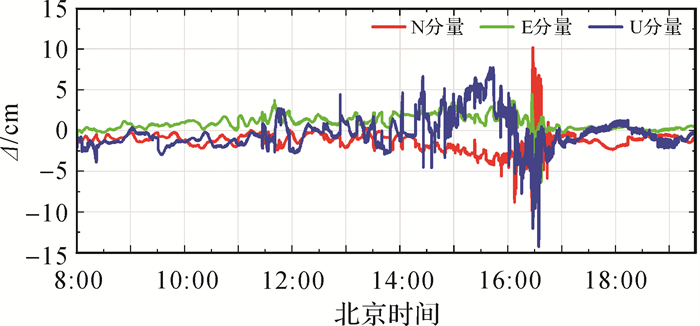
当VRS服务距离分别设置为1、3、6、9、12和15 km时,其外符合精度分别如图 4—图 7所示。图 4—图 6中,红色、绿色和蓝色曲线分别表示N分量、E分量和U分量方向的外符合精度。可见,随着VRS与流动站ROV之间的距离增加,流动站的定位精度呈现降低趋势。

|
| 图 4 VRS服务距离1 km外符合精度 Fig. 4 Positioning accuracy when the VRS service distance is 1 km |
|
| 图 5 VRS服务距离3 km外符合精度 Fig. 5 Positioning accuracy when the VRS service distance is 3 km |
|
| 图 6 VRS服务距离6 km外符合精度 Fig. 6 Positioning accuracy when the VRS service distance is 6 km |

|
| 图 7 中纬度地区1~15 km服务距离上的外符合精度趋势图 Fig. 7 The trend of positioning accuracy when the service distance increases from 1 km to 15 km in mid-latitude region |
分析外符合精度的变化与服务距离之间的关系,绘制出不同坐标分量随服务距离增加的变化趋势,如图 7所示。同时,对6组虚拟站解算流动站ROV的E、N、U方向外符合精度进行统计,结果见表 1。
| 服务距离/km | 外符合精度/mm | ||
| N方向 | E方向 | U方向 | |
| 1 | 18.01 | 8.02 | 32.83 |
| 3 | 18.69 | 13.36 | 28.68 |
| 6 | 21.33 | 14.30 | 35.20 |
| 9 | 12.45 | 28.46 | 40.73 |
| 12 | 26.62 | 25.62 | 62.15 |
| 15 | 37.26 | 42.41 | 83.01 |
由图 7和表 1可知,当服务距离达到9 km时,水平方向上的精度优于3 cm,高程方向的精度为4 cm,符合网络RTK的精度性能,但随着服务距离的进一步增加,定位精度开始下降。服务距离不超过9 km时,定位性能良好。当服务距离超过9 km时,水平和垂直方向的定位精度都呈现明显的下降趋势。
综上所述,在中纬度地区,VRS的有效服务距离不应超过9 km,对应的格网化VRS间距应设置在12 km以内。建议在一般平原丘陵地区,可采用坐标格网划分,若CORS网覆盖区地形复杂且存在小气候环境时,可采用TIN进行格网划分。
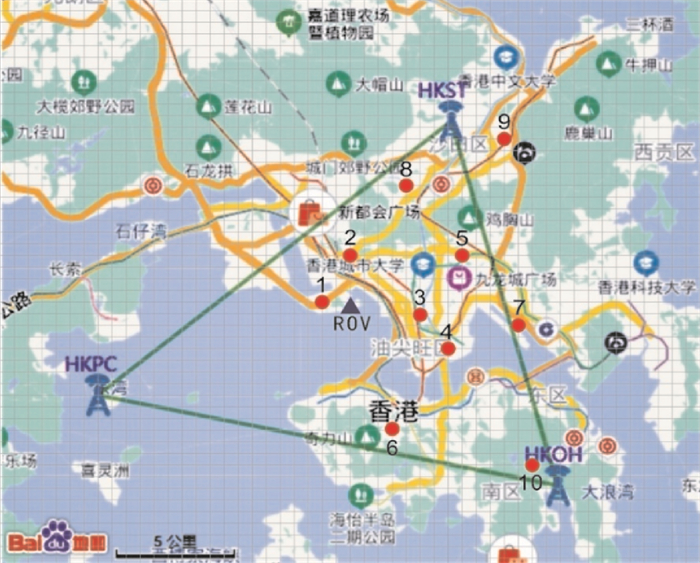
3.2 低纬度地区VRS格网化试验大气延迟具有很强的时空变化特性,尤其是电离层延迟在低纬度地区变化更为剧烈,是影响网络RTK性能的重要因数[20-24],选择我国香港地区CORS网络,以CORS网络中的3个站(HKST、HKPC、HKOH)所构成的解算单元进行测试,如图 8所示。选取HKSC点作为模拟流动站(ROV“▲”所示)进行RTK解算定位,红色圆点为选取的VRS位置,分别以ROV点平面方向1~10 km生成10个VRS,其中由近及远分别距离ROV点1、2、3、4、5、6、7、8、9和10 km。以VRS为基准,解算流动站ROV坐标,定位精度如图 9—图 12所示。
|
| 注:Ν方向外符合精度为1.55 cm; Ε方向外符合精度为0.87 cm; U方向外符合精度为3.95 cm。 图 8 低纬度地区CORS及VRS位置 Fig. 8 CORS in low latitude region and VRS location |
|
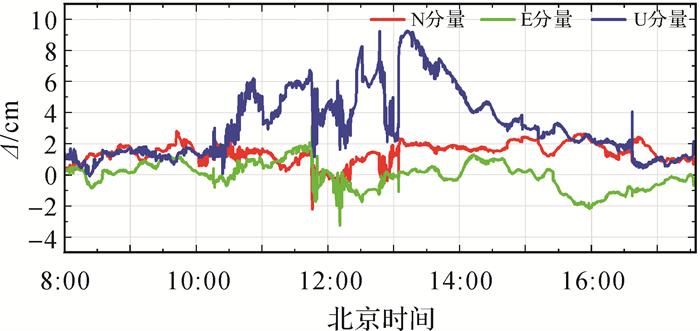
| 注:Ν方向外符合精度为1.11 cm; Ε方向外符合精度为1.52 cm; U方向外符合精度为3.94 cm。 图 9 VRS服务距离2 km外符合精度 Fig. 9 Positioning accuracy when the VRS service distance is 2 km |

|
| 图 10 VRS服务距离4 km外符合精度 Fig. 10 Positioning accuracy when the VRS service distance is 4 km |

|
| 注:Ν方向外符合精度为3.91 cm;Ε方向外符合精度为1.57 cm;U方向外符合精度为6.80 cm。 图 11 VRS服务距离6 km外符合精度 Fig. 11 Positioning accuracy when the VRS service distance is 6 km |

|
| 图 12 低纬度地区1~10 km外符合精度趋势图 Fig. 12 The trend of positioning accuracy when the service distance increases from 1 km to 10 km in low-latitude region |
由图 9—图 11可知,在低纬度地区不同的服务距离上,3个方向的符合精度均出现显著波动,且呈现随服务距离增加而增加的趋势,定位精度和性能随之下降。表明低纬度地区的定位性能显著低于中纬度地区,并且在电离层较活跃时段(图 9—图 11中,北京时间11:00—14:00),定位精度呈现明显的性能降低,说明低纬度地区的电离层影响需要特别重视和处理。对10组虚拟站解算流动站ROV的E、N、U方向外符合精度进行统计(表 2)。
| 服务距离/km | 外符合精度/mm | ||
| N方向 | E方向 | U方向 | |
| 1 | 5.69 | 4.95 | 28.22 |
| 2 | 15.46 | 8.77 | 39.50 |
| 3 | 15.24 | 12.97 | 43.22 |
| 4 | 11.10 | 15.16 | 39.44 |
| 5 | 19.79 | 13.73 | 33.02 |
| 6 | 39.05 | 15.66 | 67.99 |
| 7 | 14.98 | 18.31 | 38.97 |
| 8 | 48.28 | 34.00 | 109.92 |
| 9 | 50.23 | 32.14 | 109.93 |
| 10 | 49.96 | 37.66 | 145.63 |
由图 12和表 2可知,服务距离在4~5 km时,定位精度开始降低出现拐点;服务距离在6 km时,坐标分量的外符合精度下降至接近7 cm;服务距离不超过5 km时,定位质量总体上良好;服务距离超过5 km时,水平和垂直方向的定位精度呈现明显的下降趋势。可见,在低纬度地区,由于电离层波动相对中纬度地区剧烈,在顾及平面和高程精度的条件下,CORS网的VRS有效服务距离不应超过5 km,对应最大的格网间距为7 km。
3.3 服务精度分析当VRS有效服务距离确定后,区内流动站与格网VRS在有效服务区内时,均采用格网VRS的虚拟观测值进行流动站的RTK解算。在低纬度地区的试验中,发现在高程方向上的精度较平面精度要低,大气延迟改正在垂直梯度上还存在未模型化残余[25],可能与香港地区CORS网络的地形起伏及跨海覆盖区域的气候差异有关,有待后续研究进行分析。
在VRS有效服务距离内,统计RTK结果每个历元的坐标分量外符合差绝对值的分布百分比,见表 3和表 4。
| 坐标方向 | < 3 cm | < 5 cm | 5~10 cm | >10 cm |
| N | 98.42% | 99.69% | 0.30% | 0.01% |
| E | 68.44% | 94.45% | 5.55% | 0.00% |
| U | 60.06% | 80.15% | 17.71% | 2.24% |
| 坐标方向 | < 3 cm | < 5 cm | 5~10 cm | >10 cm |
| N | 81.85% | 99.98% | 0.02% | 0.00% |
| E | 98.63% | 100.00% | 0.00% | 0.00% |
| U | 56.09% | 87.78% | 12.07% | 0.15% |
由表 3和表 4可知,中纬度地区VRS格网间距为12 km时,RTK定位误差在N、E、U各分量优于3 cm的结果分别占比为98.42%、68.44%、60.06%;精度优于5 cm的结果则分别为99.69%、94.45%、80.15%。误差大于10 cm的历元数在U分量仅存在2.24%。低纬度地区VRS格网间距为7 km时,N、E、U误差优于5 cm的历元数分别占比为99.98%、100%、87.78%,误差大于10 cm的历元数仅在U分量存在0.15%。可见,在两个试验区确定的VRS格网间距限值是合理的,理论和试验验证表明,格网化VRS理论与算法的正确性和有效率。
4 结论本文针对网络RTK的VRS技术,提出并构建了面向广域并发用户服务的格网化VRS技术,VRS格网既可按坐标格网也可顾及复杂地形地貌条件按TIN划分。基于大气延迟梯度的VRS虚拟格网划分方法,建立了空间大气延迟与基线分量误差之间的关系,实现了基于空间误差影响的虚拟格网间距设定,并进行VRS服务精度的动态评估。通过中纬度和低纬度的两个CORS网络的试验,验证了方法的准确性、有效性和可靠性。实测网络观测数据测试结果表明:在试验区,虚拟格网间距限值分别为12 km(中纬度区)和7 km(低纬度区)。在VRS有效服务区范围,如果单个格网并发用户数为N,则VRS格网化对海量并发用户的服务能力提升(1-1/N),有效提高了VRS的服务性能。
| [1] |
YANG Yuanxi. Resilient PNT concept frame[J]. Journal of Geodesy and Geoinformation Science, 2019, 2(3): 1-7. DOI:10.11947/j.JGGS.2019.0301 |
| [2] |
杨元喜, 杨诚, 任夏. PNT智能服务[J]. 测绘学报, 2021, 50(8): 1006-1012. YANG Yuanxi, YANG Cheng, REN Xia. PNT intelligent services[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(8): 1006-1012. DOI:10.11947/j.AGCS.2021.20210051 |
| [3] |
张小红, 胡家欢, 任晓东. PPP/PPP-RTK新进展与北斗/GNSS PPP定位性能比较[J]. 测绘学报, 2020, 49(9): 1084-1100. ZHANG Xiaohong, HU Jiahuan, REN Xiaodong. New progress of PPP/PPP-RTK and positioning performance comparison of BDS/GNSS PPP[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(9): 1084-1100. DOI:10.11947/j.AGCS.2020.20200328 |
| [4] |
LAMBROU E, KANELLOPOULOS N. Check and calibration of a single GNSS receiver by using the VRS RTN positioning method[J]. Measurement, 2018, 117: 221-225. DOI:10.1016/j.measurement.2017.12.001 |
| [5] |
ÖǦÜTCÜ S, KALAYCI. Accuracy and precision of network-based RTK techniques as a function of baseline distance and occupation time[J]. Arabian Journal of Geosciences, 2018, 11(13): 354. DOI:10.1007/s12517-018-3712-2 |
| [6] |
黄丁发, 周乐韬, 卢建康, 等. GNSS卫星导航地基增强系统与位置云服务关键技术[J]. 西南交通大学学报, 2016, 51(2): 388-395. HUANG Dingfa, ZHOU Letao, LU Jiankang, et al. Key techniques of GNSS ground-based augmentation system and location based cloud service[J]. Journal of Southwest Jiaotong University, 2016, 51(2): 388-395. |
| [7] |
PU Yakun, MIN Song, YUAN Yunbin. Modified interpolation method of multi-reference station tropospheric delay considering the influence of height difference[J]. Remote Sensing, 2021, 13(15): 2994. DOI:10.3390/rs13152994 |
| [8] |
张绍成. 基于GPS/GLONASS集成的CORS网络大气建模与RTK算法实现[D]. 武汉: 武汉大学, 2010. ZHANG Shaocheng. CORS network atmospheric modeling and RTK algorithm implementation based on GPS/GLONASS integration[D]. Wuhan: Wuhan University, 2010. |
| [9] |
LU Weijun, MA Guanyi, WAN Qingtao, et al. Virtual reference station-based computerized ionospheric tomography[J]. GPS Solutions, 2021, 25(1): 8. DOI:10.1007/s10291-020-01039-1 |
| [10] |
李滢. 基于地基增强系统的格网虚拟观测值生成方法研究[D]. 郑州: 信息工程大学, 2018. LI Ying. Research on grid virtual observations generation based on ground-based augmentation system[D]. Zhengzhou: Information Engineering University, 2018. |
| [11] |
李立弘, 史俊波, 欧阳晨皓. 虚拟格网技术对网络RTK动态定位的影响分析[J]. 测绘通报, 2020(5): 115-118. LI Lihong, SHI Junbo, OUYANG Chenhao. Analysis of virtual grid technology impact on dynamic positioning of network RTK[J]. Bulletin of Surveying and Mapping, 2020(5): 115-118. DOI:10.13474/j.cnki.11-2246.2020.0157 |
| [12] |
周乐韬, 黄丁发, 李成钢, 等. 一种参考站间双差模糊度快速解算策略[J]. 大地测量与地球动力学, 2006, 26(4): 34-40. ZHOU Letao, HUANG Dingfa, LI Chenggang, et al. A strategy of double difference ambiguity resolution in reference station network[J]. Journal of Geodesy and Geodynamics, 2006, 26(4): 34-40. |
| [13] |
周乐韬. 连续运行参考站网络实时动态定位理论、算法和系统实现[D]. 成都: 西南交通大学, 2007. ZHOU Letao. Theory, algorithms and implementation of network real-time kinematic positioning based on continuously operating reference stations[D]. Chengdu: Southwest Jiaotong University, 2007. |
| [14] |
周乐韬, 黄丁发, 李成钢, 等. 基于球面Delaunay三角网的GPS网络构造算法[J]. 西南交通大学学报, 2007, 42(3): 380-383. ZHOU Letao, HUANG Dingfa, LI Chenggang, et al. Algorithm for GPS network construction based on spherical Delaunay triangulated irregular network[J]. Journal of Southwest Jiaotong University, 2007, 42(3): 380-383. |
| [15] |
黄丁发, 李成钢, 吴耀强, 等. GPS/VRS实时网络改正数生成算法研究[J]. 测绘学报, 2007, 36(3): 256-261, 339. HUANG Dingfa, LI Chenggang, WU Yaoqiang, et al. Study of the real-time network correction generation approach for GPS/VRS technique[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(3): 256-261, 339. |
| [16] |
周乐韬, 黄丁发, 徐锐, 等. 一种网络RTK新技术——增强参考站[J]. 武汉大学学报(信息科学版), 2008, 33(1): 76-80. ZHOU Letao, HUANG Dingfa, XU Rui, et al. A new network RTK-augmentation reference station[J]. Geomatics and Information Science of Wunan University, 2008, 33(1): 76-80. |
| [17] |
吴康良. ARSNet/VENUS网络RTK位置服务质量控制[D]. 成都: 西南交通大学, 2018. WU Kangliang. Quality control of ARSNet/VENUS network RTK location service[D]. Chengdu: Southwest Jiaotong University, 2018. |
| [18] |
黄丁发, 周乐韬, 刘经南, 等. 基于Internet的VRS/RTK定位算法模型及实验研究[J]. 武汉大学学报(信息科学版), 2007, 32(3): 220-224, 228. HUANG Dingfa, ZHOU Letao, LIU Jingnan, et al. Internet based VRS/RTK positioning algorithm and experiment[J]. Geomatics and Information Science of Wunan University, 2007, 32(3): 220-224, 228. |
| [19] |
张熙, 黄丁发, 廖华, 等. 一种新的GNSS相对定位解算模型[J]. 西南交通大学学报, 2015, 50(3): 485-489. ZHANG Xi, HUANG Dingfa, LIAO Hua, et al. New mathematical model for GNSS relative positioning resolving[J]. Journal of Southwest Jiaotong University, 2015, 50(3): 485-489. |
| [20] |
黄丁发, 张勤, 张小红, 等. 卫星导航定位原理[M]. 武汉: 武汉大学出版社, 2015. HUANG Dingfa, ZHANG Qin, ZHANG Xiaohong, et al. Principles of satellite navigation and positioning[M]. Wuhan: Wuhan University Press, 2015. |
| [21] |
PSYCHAS D, VERHAGEN S. Real-time PPP-RTK performance analysis using ionospheric corrections from multi-scale network configurations[J]. Sensors, 2020, 20(11): 3012. DOI:10.3390/s20113012 |
| [22] |
HOU Pengyu, ZHANG Baocheng, LIU Teng. Integer-estimable GLONASS FDMA model as applied to Kalman-filter-based short-to long-baseline RTK positioning[J]. GPS Solutions, 2020, 24(4): 93. DOI:10.1007/s10291-020-01008-8 |
| [23] |
LI Jianfeng, HUANG Dingfa, WANG Yongqian, et al. A new model for total electron content based on ionospheric continuity equation[J]. Advances in Space Research, 2020, 66(4): 911-931. DOI:10.1016/j.asr.2020.04.048 |
| [24] |
周乐韬, 黄丁发, 冯威, 等. 北斗卫星导航系统/美国全球定位系统载波相位相对定位全球精度分析[J]. 中国科学: 地球科学, 2019, 49(4): 671-686. ZHOU Letao, HUANG Dingfa, FENG Wei, et al. Global precision analysis of carrier phase relative positioning in BeiDou navigation satellite system and United States global positioning system[J]. Science China Earth Sciences, 2019, 49(4): 671-686. |
| [25] |
张熙. 多星座CORS混合观测网络实时位置服务关键技术研究[D]. 成都: 西南交通大学, 2016. ZHANG Xi. Research on key issues of multi-GNSS hybrid CORS network for real-time location service[D]. Chengdu: Southwest Jiaotong University, 2016. |


