2. 中国科学院大学地球与行星科学学院,北京 100049
2. College of Earth and Planetary Sciences, University of Chinese Academy of Sciences, Beijing 100049, China
时间频率是一个一维尺度的物理量,时间基准是由周期性的物理现象(如原子钟的频率)维持的,并通过同步或对比进行传递。利用时间服务系统将时间基准传递给用户的过程,称为授时服务,用于表述某一物理事件(如1PPS)对应的时刻,完整的授时还包括事件的日期时间信息(time of day,TOD)。准确的时间信息在通信、金融、电力、国防等诸多领域具有重要价值。新一代通信技术、精密测控及军用武器平台等领域对授时的精度提出了纳秒甚至亚纳秒级的要求[1]。全球卫星导航系统(GNSS)进行时间传递具有设备成本低、测量精度高、覆盖范围广、不受距离限制等诸多优势,是时间传递的主要技术手段之一[2-5]。传统GNSS时间传递技术包括共视法(common-view, CV)和全视法(all-in-view, AV)等基于伪距观测值的方案[6-7],其原理是通过距离的光速时延改正将卫星或基准站的时间频率传递给用户,由于卫星钟差和伪距的精度限制,时间传递精度通常在数纳秒至数十纳秒量级。近年来,基于载波的GNSS技术的发展和完善为高精度授时提供了新的契机,相比于伪距方案可以实现量级上的精度提升,已成为当前精密时间传递领域中的研究热点[8-10]。
作为对CV和AV方法的自然延伸,目前,已发展了两种基于载波相位的高精度时间传递方案:一种是基于载波差分的方式,实现两站(主副站)之间精准的钟差比对;另一种是基于精密单点定位(precise point positioning, PPP)模式,实现单站的钟差解算。其中,差分模式无须精密的钟差和轨道信息,但必须有足够的共视卫星数,作用范围有限[11]。PPP模式突破了空间范围限制,具有更高的灵活性,得到了广泛的关注和研究[12]。但是,PPP模式需要实时的精密卫星轨道与钟差产品,IGS实时数据流服务(real-time service, RTS)的正式发布,有力推动了GNSS实时精密单点定位和高精度授时的应用发展。PPP解算过程中需要有效分离出载波相位模糊度与大气延迟,待求的参数较多,数据处理较为复杂。2004—2006年国际计量局(BIPM)研究人员使用GPS PPP方法计算得到亚纳秒的时间传输精度,并指出GPS PPP用于时间传递的短期稳定度优于双向卫星时间频率比对(two-way satellite time and frequency transfer, TWSTFT)[13]。文献[14]对事后GPS精密单点定位钟差解算精度进行了分析,可获得0.1~0.2 ns的精度。在硬件研究方面,文献[15]提出一种基于锁相环的GNSS钟差校准算法。文献[16]提出并构建了基于PPP的实时高精度授时系统,实现了标准差小于1 ns、频率稳定度可达2×10-14/d的授时性能。
现有文献针对解算钟差技术描述较多,较少涉及硬件的集成与研制,并且接收机钟差一般采用在终端进行解算的方案,对处理器要求较高,硬件成本较高,解算负荷较大。本文采用云处理模式进行实时PPP解算,结合授时终端的时钟驯服技术,构建一种基于PPP的高精度授时新方案,并基于该方案,系统设计和研制一套搭载多系统GNSS接收机板卡和普通恒温晶振(oven controlled crystal oscillator, OCXO)的授时原理样机。通过短基线和与标准时标对比两个试验,验证本文研究的高精度云平台授时技术与方法及硬件系统的可行性,评估其可能达到的授时精度。
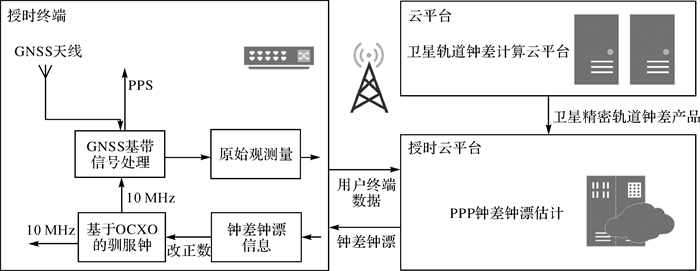
1 基于PPP的云平台授时方案采用PPP模式进行时间传递和高精度授时包含3个关键部分:实时获取导航卫星精密轨道和钟差产品,实时GNSS数据处理和接收机钟差解算,以及接收机时钟的时频同步。基于云平台搭建的分析中心通过实时处理GNSS跟踪站观测数据,生成精密卫星轨道和钟差产品发送给用户,作为GNSS导航系统的时间基准;授时云平台通过数据链接收用户授时终端GNSS观测数据,采用PPP模式计算接收机精密位置和钟差,再将解算结果发送至用户授时终端;用户授时终端采用OCXO作为本地钟,根据接收到的钟差解算结果,通过时钟驯服技术调制恒温晶振并输出准确的时间信息。PPP授时技术方案的主体架构如图 1所示。
|
| 图 1 PPP云平台授时系统架构 Fig. 1 Structure of PPP cloud platform timing system |
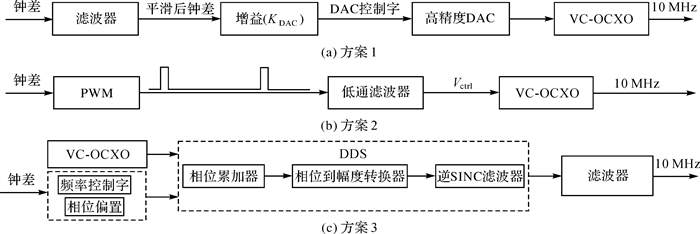
设立在中国科技云的自主部署的协同精密定位平台分析中心(武汉)通过NTRIP(Networked Transport of RTCM via Internet Protocol)协议实时播发RTCM格式的SSR改正信息,经过授时云平台在线解码处理,由广播星历恢复成精密轨道和钟差,供PPP解算使用[17]。GNSS数据解算过程中需要进行数据预处理、各项误差改正,以及建立符合实际的参数估计及随机模型[14]。利用时钟驯服技术将本地时钟与GNSS系统时钟同步。OCXO的时钟驯服有3种实现方案,如图 2所示。
|
| 图 2 基于OCXO的驯服钟的实现 Fig. 2 Implementation of OCXO steering |
3种方案的描述如下。
(1) 方案1:接收机钟差通过一个低通滤波器后转换为数模转换器(DAC)的控制字,DAC将控制字转换为VC-OCXO(压控恒温晶振振荡器)的电压,从而改变恒温晶振的输出频率,再通过频率调整改变PPS的相位。
(2) 方案2:与方案1类似,也是通过调整VC-OCXO的控制电压来改变其输出的频率,不同的地方是用一个PWM(脉宽调制器),输出占空比不同的方波信号,该方波信号经过低通滤波器后输出控制电压。
(3) 方案3:与方案1、2不同,通过DDS(direct digital synthesis)采用数字的方式产生时钟,生成10 MHz的频率源,该方式通过频率控制字和相位偏置能同时控制时钟的频率和相位,可以加速钟差的收敛过程。该方案控制精度更高,收敛速度更快。
3种方案的性能对比见表 1,本文研究采用了方案3。
| 方案 | 驯服方式 | 收敛时间 | 硬件复杂度 | 成本 |
| 方案1 | 频率改正 | 慢 | 低 | 中 |
| 方案2 | 频率改正 | 慢 | 中 | 低 |
| 方案3 | 频率改正+相位改正 | 快 | 中 | 高 |
1.1 实时精密轨道与钟差计算
卫星实时精密轨道和钟差改正数通常编码成RTCM格式的SSR(state-space representation)改正数,使用NTRIP协议播发给全球用户使用。SSR可以通过各家分析中心获取,例如IGSCB(IGS Central Bureau)、BKG(Bundesamt für Kartographie und Geodäsie)和CNES(Centre National d'Études Spatiales)等。IGS分析中心发布的实时卫星轨道产品精度一般优于5 cm,实时卫星钟差产品精度优于0.2 ns[18]。首先在云平台上使用广播星历计算出卫星的轨道和钟差,然后使用改正数进行修正即可得到精密的轨道和钟差数据[17, 19]。广播星历的参考坐标系为地心地固系(Earth centered earth fixed,ECEF),SSR改正数基于轨道坐标系,因此需要进行坐标系转换。观测时刻轨道坐标系下的改正数δO(t)和ECEF坐标系下的改正数δX(t)可以表示为
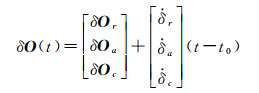 (1)
(1)
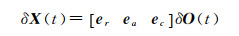 (2)
(2)
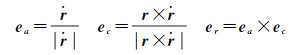 (3)
(3)
式中,δOr、δOa、δOc分别为轨道坐标系参考时刻t0对应的径向、切向和法向改正数;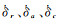
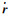
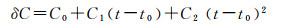 (4)
(4)
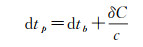 (5)
(5)
式中,C0、C1、C2为t0时刻对应的改正数系数;δC为卫星钟差改正数,单位为m;dtp为精密卫星钟差;dtb为广播星历计算钟差;c为光速。
1.2 PPP接收机钟差解算接收机原始观测数据主要包括伪距(Pf, rs)和载波(Lf, rs)观测值,非差观测方程可以表示为[19]
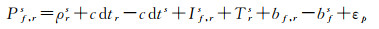 (6)
(6)
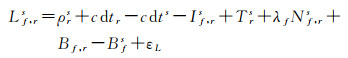 (7)
(7)
式中,s、f、r分别表示卫星号、导航信号频段及接收机编号;ρrs是卫星天线到接收机天线之间的距离(站星距);c是光速;dtr和dts分别是接收机和卫星钟差;If, rs是卫星信号方向的电离层延迟;Trs是卫星信号方向的对流层延迟;bf, r和bfs分别是接收机端和卫星端伪距硬件延迟;Bf, r和Bfs分别是接收机端和卫星端相位硬件延迟;λf是频率f对应的载波波长;Nf, rs是频率f对应的载波整周模糊度;εp和εL是伪距和载波观测噪声。其他误差包括相对论改正、地球自转改正,卫星和接收机天线相位中心改正、天线高改正等已使用模型改正,在计算站星距ρrs时应加以考虑[20]。
GNSS观测值采用消电离层组合的模式,可以消除电离层延迟误差一阶项,电离层延迟的高阶误差影响在毫米级,可以忽略不计[22]。消除电离层延迟的伪距和载波观测值可以写成如下形式
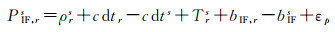 (8)
(8)
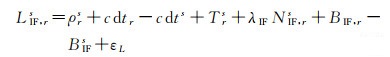 (9)
(9)
消电离层组合的PPP观测方程中接收机钟差吸收了部分硬件延迟,在实际数据处理过程中,接收机钟差参数包含了接收机端的硬件延迟,发布的卫星钟差也包含了卫星端的硬件延迟,即
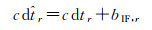 (10)
(10)
 (11)
(11)
消电离层模糊度参数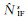
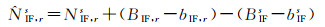 (12)
(12)
参数重组后的伪距和载波观测方程为
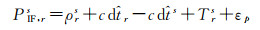 (13)
(13)
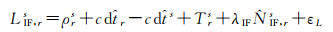 (14)
(14)
解算得到的接收机钟差包含了天线电缆和接收机硬件延迟(统称为授时终端的硬件延迟),可以认为是一个常数,并可利用已知时标进行事先标定,在终端时钟驯服的DSP编程时可将标定好的硬件延迟作为一个输入参数加以扣除。在PPP钟差解算中,采用GPS和BDS联合解算方式,待估未知数包括坐标未知数、接收机钟差(每个卫星系统均设置一个接收机钟差参数)、消电离层浮点模糊度未知数、对流层天顶延迟参数,参数估计采用卡尔曼滤波处理方法。
1.3 本地时钟驯服授时云平台负责PPP解算接收机坐标和钟差,并将结果发送到授时终端,授时终端根据接收机钟差来调整本地时钟晶振的频率和相位,从而将本地时间与GNSS时间基准对齐。由于成本和使用场景限制,授时终端的时钟通常采用稳定度较低的晶振,其频率长期稳定度较差,需要通过时钟驯服技术来抑制频率偏移引起的时间偏差。
GNSS驯服时钟的基本结构实际上是一个参考频率含有一定噪声的低频锁相环[21-23],工作原理如图 3所示[24]。首先对OCXO输出的原始10 MHz进行倍频,倍频后作为DDS核的工作时钟。根据奈奎斯特采样定律,工作时钟要大于20 MHz,考虑到采样点数及量化噪声,本方案选择4倍频,即系统工作时钟(Fsysclk)为40 MHz。DDS产生的时钟的分频率取决于相位累加器的位数,本方案选择累加器位数为48位,则频率分频率为Fres=Fsysclk×2-48=0.142 uHz,相对10 MHz其调整精度为0.014 2×10-6。DDS除了可以直接进行频率修正还可以进行相位修正,本方案中相位修正量为14 bit,该值直接加到相位累加器的高14位,对于10 MHz的时钟来说,可以调整的时间分辨率为Tres=0.1 us×2-14=6 ps,精度已经超过钟差解算的精度。
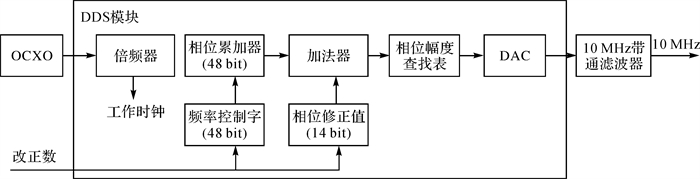
|
| 图 3 晶振驯服基本原理 Fig. 3 The diagram of clock steering |
整个时钟驯服的工作过程如下。
(1) 上电后接收机首先进行钟差的粗调,调整的时间分辨率等于基带工作时钟的周期,假设接收机的工作时钟为40 MHz,则调整精度为25 ns。
(2) 当钟差在大约25 ns范围以后,启动驯服晶振过程,驯服过程分为3个步骤:
首先,进行频率调整,该步骤的输入是接收机钟漂,采用一阶锁频环,公式如下
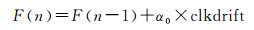 (15)
(15)
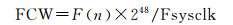 (16)
(16)
式中,α0为一阶锁频环的环路系统,选择的原则是频率的调整量不能超过接收机基带环路的牵引范围,过大容易导致接收机失锁;clkdrift为钟漂值;Fsysclk为系统工作时钟;F(n)是计算出来的频率值,FCW是频率控制字。
其次,当clkdrift的数字趋于Fres时转入相位调整,利用相位修正逐步把接收机的钟差修正到0附近,通过前面的分析可知,时间调整的精度为Tres,调整范围为(-100, +100) ns。需要注意的是每次调整相位值换算到L频段不能超过45°,否则会引起接收机锁相环的失锁,以GPS L1为例,对应的相位调整量为0.08 ns,该值虽然不至失锁但是会是使环路短暂振荡,因此调整量应当缩小。
最后,当clkbias逐渐趋于Tres时,转入锁相环阶段,锁相环用于跟踪clkdrift和clkbias,驯服完好时,接收机钟差理论上应为零,由于噪声和硬件分辨率误差,实际上仅能接近于零。本方案采用三阶锁相环,三阶锁相环的优势在于可以提供钟漂和钟漂的一阶导数,这些值可以对时钟进行预测和保持。
根据上述步骤最终实现GNSS卫星授时长期稳定性高和本地晶振短期稳定度高的优势互补。
1.4 本地时钟维持由于实时PPP依赖于网络接收精密服务产品,并且GNSS接收机对卫星信号观测较为苛刻,一旦产品或观测值不稳定导致PPP实时解算故障,则会导致钟差无法实时估计。此时只能依赖OCXO维持短时的高精度时间信息输出。通过对OCXO的频率漂移进行建模补偿,可以显著降低其短期漂移,提升时间信息维持的精度[25]。因此PPP解算钟差除了用于消除累积的误差,也用来估计OCXO的频率偏差和老化率。
晶振特性主要是指其真实频率相对于其标称频率的偏差。这些偏差可以分为两类,即系统偏差和随机误差[26]。将GNSS解算的钟差作为量测信息,对晶振模型参数进行估计,量测模型可以表示为[24]
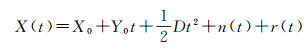 (17)
(17)
式中,X0为初始频率;Y0为频率偏差;D为频率老化系数;n(t)为晶振噪声;r(t)为GNSS接收机钟差解算误差。式(17)右侧的前3项影响时钟的系统偏差,而晶振的随机误差主要取决于晶振幂律噪声,接收机钟差受卫星钟差、大气延迟、接收机本身误差等因素共同影响。通过对本地接收机钟进行建模,可以尽可能长时间维持高精度的授时。
2 试验结果与分析授时终端原型样机由控制板卡、电源模块、DSP处理器、GNSS接收机板卡、恒温晶振和DTU通信模块组成,终端硬件接口包括:GNSS天线输入口、1PPS输出接口、电源指示灯、GNSS信号灯、无线网络接口、串口和USB调试接口。
实时精密卫星产品采用武汉协同精密定位平台发布的SSR改正产品,该产品与IGS分析中心发布的产品精度相当。为了验证授时方案的授时精度,设计两组试验:①使用两台授时终端进行短基线时间比对,各自进行PPP授时,在短基线情况下,两台接收机受到大气延迟误差和时间基准误差的影响大致相同,可评估授时终端间的相对授时精度。②使用单台授时终端输出的1 PPS与国家授时中心的UTC输出的1 PPS进行时差比较,可评估授时终端的绝对授时精度。
2.1 试验1使用两台授时终端进行短基线时间比对测试,测试时间为2022年3月18日18时至2022年3月19日18时,共24 h。测试地点为中国科学院精密测量科学与技术创新研究院1号楼楼顶,基线距离约为30 m,授时终端测试场景如图 4所示。将两天线分别接入两台授时终端,接通电源后将两台接收机输出的1 PPS接入时间频率间隔计数器(型号:SR620),测量并记录两台授时终端的时差,接收机钟驯服收敛后的时差时间序列如图 5所示。

|
| 图 4 授时终端短基线测试场景 Fig. 4 Test scenario of GNSS timing receivers with short baseline |
|
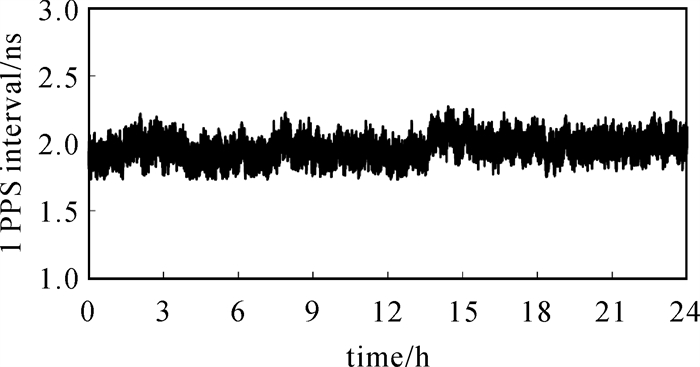
| 图 5 短基线情况下两台授时终端时间比对结果 Fig. 5 Time difference between two GNSS timing receivers with short baseline |
由图 5可知,两台授时终端共进行了24 h的时间比对,两者的PPS时差峰峰值为0.54 ns,STD值为0.08 ns,表明两台授时终端间的相对授时精度较高,验证了本文提出方案的可行性和有效性。
精密单点定位授时的实质是让接收机钟差与理想卫星钟同步,经时钟驯服后,解算的绝对钟差应为零。绝对钟差的波动情况也反映了单台授时终端是否稳定,图 6是该试验时段两台授时终端解算的绝对钟差时间序列。
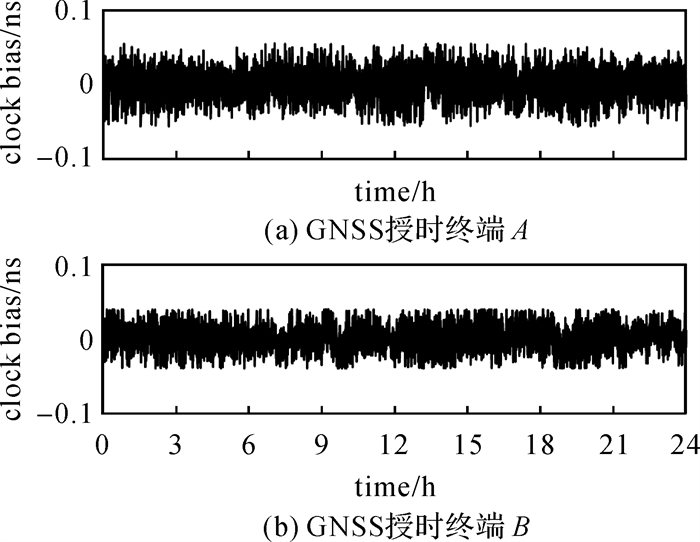
|
| 图 6 授时终端钟差结果 Fig. 6 Clock offset of GNSS timing receiver |
由图 6中可以看出,在24 h内,两台授时终端的绝对钟差变化幅度较小,整体看来呈一条直线。经计算得到该段时间内授时终端A的钟差序列的峰峰值为0.11 ns,STD值为0.02 ns,授时终端B的钟差序列的峰峰值为0.08 ns,STD值为0.01 ns。表明解算得到的接收机钟差精度优于0.1 ns,同时也表明授时终端达到了亚纳秒的精度。
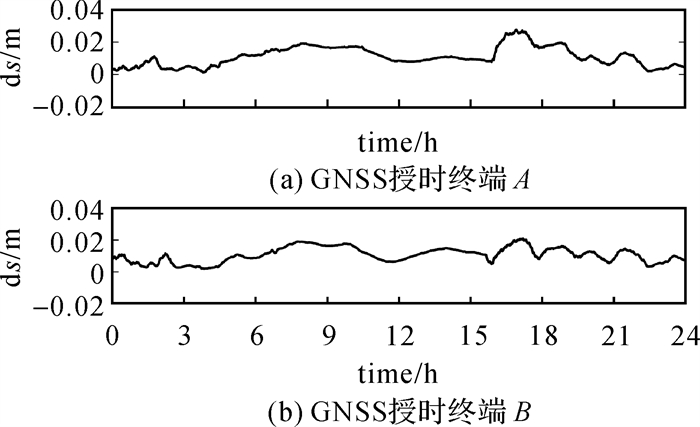
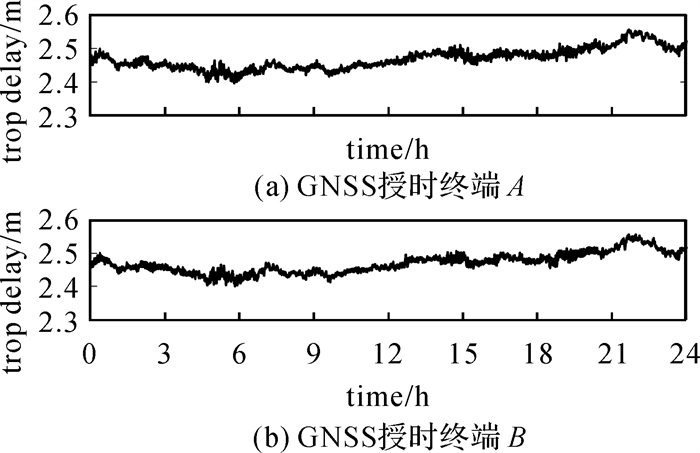
图 7给出了两台授时终端的三维位置误差序列,图 8给出了两台授时终端解算得到的对流层延迟序列。
|
| 图 7 授时终端三维位置误差 Fig. 7 3D position errors of GNSS timing receivers |
|
| 图 8 授时终端解算的对流层延迟序列 Fig. 8 Tropospheric delay sequences solved by GNSS timing receivers |
由图 7可以看出,两台授时终端解算得到的坐标精度均为厘米级,图 8中两台接收机解算得到的对流层延迟非常接近,差别在1 cm以内。两台授时终端均为PPP独立解算,坐标和对流层精度都在厘米级,表明算法在一定程度上分离了钟差与大气误差的耦合关系。
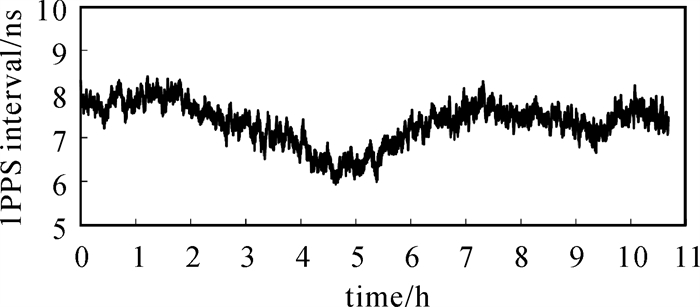
2.2 试验2试验1进行了在短基线条件下两台授时终端的时间比对,反映出授时终端间的相对授时精度。为验证授时终端的绝对授时精度,以西安授时中心的UTC时间作为参考,采用PPP解算得到的GPS钟差进行调钟,使授时终端输出的1 PPS与GPS时标对齐,测试单台授时终端的授时精度。测试时间为2021年6月30日,测试时长约为11 h,使用时间频率间隔计数器(SR620)记录授时终端1 PPS与标准UTC 1PPS的时差,如图 9所示。
|
| 图 9 授时终端1PPS与UTC 1PPS比对结果 Fig. 9 Time difference between the GNSS timing receiver 1PPS and UTC 1PPS |
由图 9可以看出,时间频率间隔计数器的结果较为稳定,在约11 h的测试中,时差的波动范围在2.5 ns以内,统计得到STD值为0.48 ns,相比于短基线情况下精度有所降低。图 5和图 9中存在的常偏是由天线电缆及接收机硬件延迟决定,可以事先标定并在时钟驯服时设置参数补偿。GPS时和UTC时本身就有一定的差异,由于UTC基准误差,授时终端的绝对授时精度略差于短基线情况下授时终端的相对授时精度,但仍达到了亚纳秒的授时精度。
3 结论本文提出的云平台授时解决方案利用协同精密定位平台发布的实时卫星轨道与钟差产品,在云端实现了实时PPP解算,不仅可以获得厘米级的坐标解,同时还可以获得高精度的接收机钟差,接收机钟差解算内符合精度可达到0.1~0.2 ns,短基线两站独立解算的对流层延迟非常接近,差别在1 cm以内,表明在一定程度上分离了钟差与大气误差的耦合关系。通过云平台将接收机钟差传输至授时终端,在接收机终端通过恒温晶振时钟驯服技术获得与理想导航卫星时间系统同步的秒脉冲。采用短基线互差比较和与UTC比较试验表明,授时精度可达到亚纳秒级,短基线的比对精度高于与UTC的比对精度,可能因为UTC和导航卫星时间系统之间存在一定差异,也可能是大气误差的残余影响,需要做进一步分析。高精度云平台授时方案优点明显,不仅能够减少终端的数据处理负担,降低终端硬件成本,而且平台软件也易于更新管理。随着5G通信技术的日益成熟,数据通信更加快捷稳定,同时,区域CORS站点的增加也为实现精密的电离层模型和对流层模型改正提供了有力的保障,因此有望通过单频PPP解算达到或接近双频的精度。
云平台授时方案也有一定的局限性,该方案要求将观测数据发送至云处理平台进行解算,再将解算结果传回终端进行调钟,不可避免会受到网络信号的影响,当网络中断时,云平台授时方案便无法进行实时解算。
| [1] |
施闯, 张东, 宋伟, 等. 北斗广域高精度时间服务原型系统[J]. 测绘学报, 2020, 49(3): 269-277. SHI Chuang, ZHANG Dong, SONG Wei, et al. BeiDou wide-area precise timing prototype system[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(3): 269-277. DOI:10.11947/j.AGCS.2020.20180534 |
| [2] |
杨旭海, 李孝辉, 华宇, 等. 卫星授时与时间传递技术进展[J]. 导航定位与授时, 2021, 8(4): 1-10. YANG Xuhai, LI Xiaohui, HUA Yu, et al. Technical progress of satellite time service and time transfer[J]. Navigation Positioning and Timing, 2021, 8(4): 1-10. |
| [3] |
杨元喜. 弹性PNT基本框架[J]. 测绘学报, 2018, 47(7): 893-898. YANG Yuanxi. Resilient PNT concept frame[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(7): 893-898. DOI:10.11947/j.AGCS.2018.20180149 |
| [4] |
张鹏飞, 涂锐, 高玉平, 等. 基于北斗的时间传递方法及其精度分析[J]. 仪器仪表学报, 2017, 38(11): 2700-2706. ZHANG Pengfei, TU Rui, GAO Yuping, et al. BeiDou time transfer method and its accuracy analysis[J]. Chinese Journal of Scientific Instrument, 2017, 38(11): 2700-2706. DOI:10.3969/j.issn.0254-3087.2017.11.011 |
| [5] |
杨俊, 单庆晓. 卫星授时原理与应用[M]. 北京: 国防工业出版社, 2013. YANG Jun, SHAN Qingxiao. Satellite timing principle and application[M]. Beijing: National Defense Industry Press, 2013. |
| [6] |
ALLAN D W, WEISS M A. Accurate time and frequency transfer during common-view of a GPS satellite[C]//Proceedings of the 34th Annual Symposium on Frequency Control. Philadelphia, PA, USA: IEEE, 1980: 334-346.
|
| [7] |
PETIT G, JIANG Z. GPS All in view time transfer for TAI computation[J]. Metrologia, 2008, 45(1): 35-45. DOI:10.1088/0026-1394/45/1/006 |
| [8] |
ZHANG Ming, LV Jinhu, BAI Zhengdong, et al. An overview on GNSS carrier-phase time transfer research[J]. Science China Technological Sciences, 2020, 63(4): 589-596. DOI:10.1007/s11431-019-9655-1 |
| [9] |
ZHANG Pengfei, TU Rui, GAO Yuping, et al. Performance of Galileo precise time and frequency transfer models using quad-frequency carrier phase observations[J]. GPS Solutions, 2020, 24(2): 40. DOI:10.1007/s10291-020-0955-7 |
| [10] |
GE Yulong, ZHOU Feng, DAI Peipei, et al. Precise point positioning time transfer with multi-GNSS single-frequency observations[J]. Measurement, 2019, 146: 628-642. DOI:10.1016/j.measurement.2019.07.009 |
| [11] |
DEFRAIGNE P, BAIRE Q. Combining GPS and GLONASS for time and frequency transfer[J]. Advances in Space Research, 2011, 47(2): 265-275. DOI:10.1016/j.asr.2010.07.003 |
| [12] |
赵传宝, 盛传贞, 张宝成. 基于接收机钟差约束的精密单点定位时间传递研究[J]. 全球定位系统, 2021, 46(2): 13-17. ZHAO Chuanbao, SHENG Chuanzhen, ZHANG Baocheng. Precise point positioning time transfer based on receiver clock offsets constraint[J]. GNSS World of China, 2021, 46(2): 13-17. |
| [13] |
PETIT G, JIANG Z. GPS all in view time transfer for TAI computation[J]. Metrologia, 2008, 45(1): 35-45. DOI:10.1088/0026-1394/45/1/006 |
| [14] |
张小红, 蔡诗响, 李星星, 等. 利用GPS精密单点定位进行时间传递精度分析[J]. 武汉大学学报(信息科学版), 2010, 35(3): 274-278. ZHANG Xiaohong, CAI Shixiang, LI Xingxing, et al. Accuracy analysis of time and frequency transfer based on precise point positioning[J]. Geomatics and Information Science of Wuhan University, 2010, 35(3): 274-278. |
| [15] |
向为, 徐博, 牟卫华, 等. 基于锁相环的GNSS授时接收机钟差校准算法[J]. 国防科技大学学报, 2013, 35(2): 115-119. XIANG Wei, XU Bo, MOU Weihua, et al. A clock error calibration algorithm based on phase lock loop in GNSS time synchronization receiver[J]. Journal of National University of Defense Technology, 2013, 35(2): 115-119. DOI:10.3969/j.issn.1001-2486.2013.02.021 |
| [16] |
GUO Wenfei, SONG Weiwei, NIU Xiaoji, et al. Foundation and performance evaluation of real-time GNSS high-precision one-way timing system[J]. GPS Solutions, 2019, 23(1): 23. DOI:10.1007/s10291-018-0811-1 |
| [17] |
WANG Zhiyu, LI Zishen, WANG Liang, et al. Assessment of multiple GNSS real-time SSR products from different analysis centers[J]. ISPRS International Journal of Geo-Information, 2018, 7(3): 85. DOI:10.3390/ijgi7030085 |
| [18] |
舒宝, 王利, 张勤, 等. SSR延迟下的轨道钟差外推误差及其对多GNSS实时精密单点定位的影响评估[J]. 测绘学报, 2021, 50(12): 1738-1750. SHU Bao, WANG Li, ZHANG Qin, et al. Evaluation of multi-GNSS orbit and clock extrapolating error and their influence on real-time PPP during outages of SSR correction[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(12): 1738-1750. DOI:10.11947/j.AGCS.2021.20200580 |
| [19] |
ELSOBEIEY M, AL-HARBI S. Performance of real-time precise point positioning using IGS real-time service[J]. GPS Solutions, 2016, 20(3): 565-571. DOI:10.1007/s10291-015-0467-z |
| [20] |
LI Pan, ZHANG Xiaohong. Integrating GPS and GLONASS to accelerate convergence and initialization times of precise point positioning[J]. GPS Solutions, 2014, 18(3): 461-471. DOI:10.1007/s10291-013-0345-5 |
| [21] |
XIAO Gongwei, LIU Genyou, OU Jikun, et al. MG-APP: an open-source software for multi-GNSS precise point positioning and application analysis[J]. GPS Solutions, 2020, 24(3): 66. DOI:10.1007/s10291-020-00976-1 |
| [22] |
HOQUE M M, JAKOWSKI N. Higher order ionospheric effects in precise GNSS positioning[J]. Journal of Geodesy, 2007, 81(4): 259-268. DOI:10.1007/s00190-006-0106-0 |
| [23] |
崔保健, 王玉珍. GPS驯服铷钟频标数据处理方法研究[J]. 电子测量与仪器学报, 2010, 24(9): 808-813. CUI Baojian, WANG Yuzhen. Study on data processing method of GPS disciplined rubidium frequency standard[J]. Journal of Electronic Measurement and Instrument, 2010, 24(9): 808-813. |
| [24] |
薛毅聪, 龚航, 刘增军, 等. 基于GNSS的晶振驯服方法分析[J]. 全球定位系统, 2017, 42(4): 38-42. XUE Yicong, GONG Hang, LIU Zengjun, et al. Analysis of disciplined crystal oscillator method based on GNSS[J]. GNSS World of China, 2017, 42(4): 38-42. |
| [25] |
冯雪阳. 基于GPS秒脉冲的恒温晶振驯服和自适应保持技术研究与实现[D]. 成都: 电子科技大学, 2014. FENG Xueyang. Research and implementation on lock and self-adaptive hold technique of oven controlled crystal oscillator based on 1PPS derived from GPS[D]. Chengdu: University of Electronic Science and Technology of China, 2014. |
| [26] |
ALLAN D W. Time and frequency (time-domain) characterization, estimation, and prediction of precision clocks and oscillators[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 1987, 34(6): 647-654. DOI:10.1109/T-UFFC.1987.26997 |


