2. 大地测量与地球动力学国家重点实验室,湖北 武汉 430077;
3. 武汉大学测绘遥感信息工程国家重点实验室,湖北 武汉 430079;
4. 山东大学空间科学研究院,山东 威海 264209
2. State Key Laboratory of Geodesy and Earth's Dynamics, Innovation Academy for Precision Measurement Science and Technology, Chinese Academy of Sciences, Wuhan 430077, China;
3. State Key Laboratory of Information Engineering in Surveying, Mapping, and Remote Sensing, Wuhan University, Wuhan 430079, China;
4. Institute of Space Science, Shandong University, Weihai 264209, China
精密单点定位(precise point positioning,PPP)技术于20世纪90年代提出并实现,依赖于高精度卫星轨道、钟差等产品,在精细化考虑各类误差改正的基础上,利用单台GNSS接收机可实现全球高精度绝对定位[1-2]。目前,PPP技术在广域精密定位、低轨卫星定轨、水汽反演与电离层监测、地震与海啸监测和预警、时间传递等领域已获得广泛应用[3-7]。
与差分定位技术(如实时动态定位RTK)相比,PPP估计参数较多且参数之间存在较强的相关性,导致位置解收敛较慢(一般为20~30min),收敛阶段位置精度提升缓慢。近年发展起来的PPP模糊度固定技术可以有效加快收敛速度、改善定位精度,引起了国内外学者和研究机构的广泛关注[8-12]。然而,PPP性能严重依赖外部高精度产品,如卫星轨道、钟差等,导致浮点模糊度解精度相对较低,PPP模糊度固定解存在可靠性风险[13]。卫星轨道、钟差产品及误差模型改正精度对模糊度浮点解偏差影响较大,进一步增大了模糊度固定可靠性提升的难度[14]。当前PPP模糊度固定的常见做法是,在获取浮点模糊度之后,进一步将其分解为宽巷和窄巷模糊度,分别引入宽巷与窄巷小数偏差改正后,对宽巷模糊度进行取整固定,对窄巷模糊度用LAMBDA降相关搜索实现固定[8, 15]。针对载波相位模糊度处理难题,研究人员尝试引入更多方法以便可靠解决此问题。文献[16]将整数等变估计(BIE)方法引入GNSS模糊度估计,并从理论上给出其严密计算公式。早期研究集中在利用BIE解决RTK模糊度固定问题。事实上,大部分中短基线RTK模糊度固定的成功率都比较高,并且双差后的残余误差基本可以忽略。在这种条件下,将模糊度固定为整数无疑是最优选择。但是PPP解算模型强度较弱,模糊度解算成功率相对较低。模糊度浮点解的质量受到服务端产品精度、接收机噪声、观测环境等因素影响,模糊度浮点解中包含的残余误差很难彻底消除,因此,直接固定PPP模糊度在观测条件相对不太理想的情况下仍存在巨大挑战。长期以来,模糊度解算的主要结果就是固定解和浮点解两种。对于PPP模糊度固定解可靠性不高的场景,采用整数等变估计反而具有一定的性能优势。整数等变估计的思想是利用整数解加权融合方法提升浮点模糊度估计精度,该方法降低了模糊度错误固定风险[16-17],同时又利用了模糊度整数解信息来提升模糊度估值精度,因此可以获得比模糊度浮点解更优的定位结果。
近年来,也有学者尝试将BIE法用于PPP模糊度估计,来缩短PPP收敛时间,但并未系统分析BIE法对PPP定位性能的提升效果[17-19]。BIE法在具体实现过程中,具有对模型进行一些近似来取得模型精度和计算效率之间的平衡。从计算效率角度来说,BIE计算效率取决于模型强度。本文为了最大程度保障BIE结果最优性,采用了推荐的给定显著性水平阈值的方式来确定BIE计算中参与的模糊度整数解向量组数。该方法的截断误差是可控的,但是效率并不一定最优。关于解决耗时问题,近期也有学者建议采用权比值方法减少参与计算的整数向量个数[19],但该方法的有效性还有待进一步验证。
基于BIE估计原理,本文首先推导PPP模糊度估计的BIE方法。然后,采用全球均匀分布的105个MGEX测站一周观测数据进行PPP解算,分析BIE法相比LAMBDA固定对PPP收敛性能的改善,并综合评估BIE法与LAMBDA固定对PPP收敛后定位精度的贡献。
1 PPP模糊度估计的BIE方法本文首先给出BIE估计原理,然后介绍PPP模糊度估计的BIE方法,最后给出其基本计算流程。本文模糊度估计研究仅限于单GPS无电离层组合星间单差PPP模糊度估计,该方法具有普适性,可扩展至多系统、非差或非组合PPP模糊度估计。
1.1 BIE估计原理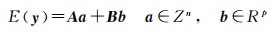 (1)
(1)
式中, y为m维GNSS观测值向量;E(·)为数学期望运算符;a和b分别为n维整数和p维实数待估参数向量。整数参数在GNSS精密定位模型中一般指载波相位模糊度参数,而实数参数则包含坐标、接收机钟差、对流层延迟等参数。A和B为整数和实数参数对应的设计矩阵。该混合整数模型的典型解法包括浮点解求解、整数模糊度估计、整数模糊度检验和实数参数更新4个步骤。为了保证整数估计的可靠性,一般在模糊度解算成功率比较高的时候,才尝试将整数模糊度参数固定为整数;当模糊度解算成功率不高时,用户通常更倾向于使用浮点解而不是固定解。这种情况下的替代方法是使用BIE方法[16]进行模糊度估计。假设模糊度浮点解服从正态分布,对于给定的模糊度浮点解â及其方差协方差矩阵Qââ, 采用BIE法得到的模糊度估计值为
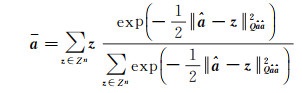 (2)
(2)
式中,a为BIE加权浮点解模糊度向量;z为任意一组n维整数向量。
文献[16]证明了BIE估计量具有无偏特性,且BIE在所有整数等变估计类中具有最小均方误差。由于整数估计与线性估计均属于整数等变估计的特例,因此BIE估计的均方误差理论上应小于整数最小二乘估计和浮点解的均方误差最小二乘估计量,由此可得[16]
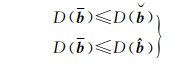 (3)
(3)
式中, D(·)为方差算子。当成功率非常高时,BIE估计量与整数最小二乘解比较接近;而当成功率不高时,BIE的结果则与模糊度浮点解比较接近[16]。
BIE的求解过程涉及整个整数空间的无限个整数备选向量的加权求和,在实际计算中需要进行适当的简化。文献[21]指出可以利用有限整数集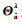
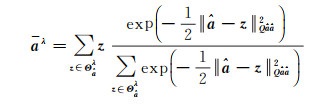 (4)
(4)
该式利用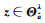
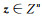
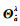
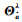
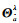
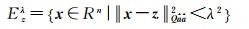 (5)
(5)
落在相应椭球区域的整数向量,即为备选整数集合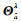
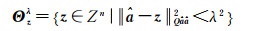 (6)
(6)
式中,阈值λ2可由给定的弃真概率α(即显著性水平)确定。一般情况下,α和阈值λ2的关系可表示为
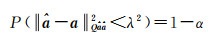 (7)
(7)
式中,a为模糊度真值。在BIE中,一般情况下α取一个比较小的数,推荐使用10-9来平衡计算复杂度和BIE的最优特性[23]。
1.2 PPP模糊度估计的BIE方法GNSS非差双频无电离层组合载波与伪距观测方程可表达为[24]
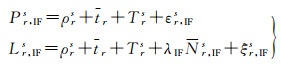 (8)
(8)
式中
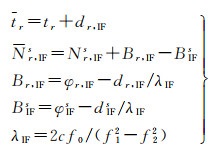 (9)
(9)
式中,s,r和IF分别代表卫星、接收机和无电离层组合标识号;Pr, IFs和Lr, IFs分别为改正了卫星钟差、卫星和接收机天线相位中心改正、相对论效应、潮汐负荷形变(固体潮、极潮和海潮)、萨奈克效应(Sagnac effect)、卫星天线相位缠绕(仅对载波观测值)等的无电离层组合伪距和载波相位观测值;ρrs表示卫星到接收机的几何距离;tr为接收机钟差;Trs为视线方向对流层斜延迟;dr和ds分别表示接收机和卫星伪距硬件延迟,相应地,φr和φs分别为接收机和卫星相位硬件延迟;Nr, IFs为无电离层组合载波相位模糊度;c和f分别表示真空中光速与载波频率,f0=10.23MHz为基准频率;εr, IFs和ξr, IFs分别为伪距和载波相位观测值对应的观测噪声和多路径效应等非建模综合误差。式中各变量的单位均为m。
PPP模糊度解算可分为以下4个步骤进行:
(1) 将无电离层组合浮点模糊度Nr, IFs分解为宽巷与窄巷模糊度的线性组合,即
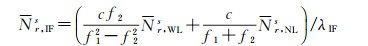 (10)
(10)
式中,Nr, WLs和Nr, NLs分别为宽巷与窄巷浮点模糊度。
(2) 宽巷模糊度固定。式(10)中宽巷模糊度Nr, WLs可进一步表达为
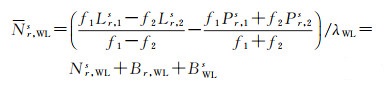 (11)
(11)
一般通过卫星间做差或设定基准来消除接收机端Br, WL的影响,利用外部产品改正卫星端BWLs。由于宽巷波长λWL较长,约为86cm,可通过取整法直接固定宽巷模糊度。
(3) 窄巷模糊度估计。在宽巷模糊度固定后,可通过式(12)实现窄巷模糊度估计
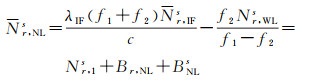 (12)
(12)
同样,可通过卫星间做差或设定基准来消除接收机端Br, NL的影响,引入外部产品改正卫星端BNLs。由于窄巷波长较短,约为10cm,直接取整固定窄巷模糊度风险较大。
(4) 重构无电离层组合模糊度。待宽巷、窄巷模糊度同时固定/估计后,可得固定后的无电离层组合模糊度
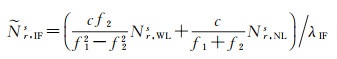 (13)
(13)
在更新无电离层组合模糊度后,其他参数(如位置、接收机钟差、对流层延迟参数等)可同步更新。
在PPP模糊度解算过程中,宽巷模糊度一般采用取整法直接确定,而窄巷模糊度则可以使用取整法、整数Bootstrapping方法或者LAMBDA降相关搜索实现[11, 15]。本文主要引入BIE方法实现窄巷模糊度的精确估计,其工作流程与LAMBDA方法相似,但是估计方法存在一定差异。
BIE方法也需要利用PPP窄巷模糊度浮点解及其方差协方差矩阵,首先对其进行降相关处理,然后利用整数最小二乘搜索确定整数备选集合。在整数集确定后,使用Z变换的逆变换将模糊度整数解变回到模糊度浮点解域[25]。接下来并不是选择最优整数备选值计算固定解坐标,而是通过式(4)确定相应备选整数解对应的加权浮点模糊度解,再将BIE确定的模糊度浮点解代入观测方程求解坐标等实数参数。
可以看出,虽然本节的推导过程基于双频观测值,但PPP模糊度估计的BIE方法并不仅限于双频观测值,对于可采用LAMBDA固定方法的PPP数据解算(如单频、三频PPP模糊度固定),同样可采用BIE方法。
2 试验结果分析 2.1 数据介绍及处理策略为验证BIE对PPP定位性能的提升效果,本文选取全球均匀分布的105个MGEX测站2021年2月第1周(DOY 32—DOY 38)采样间隔为30s的观测数据进行数据处理,测站地理分布如图 1所示。
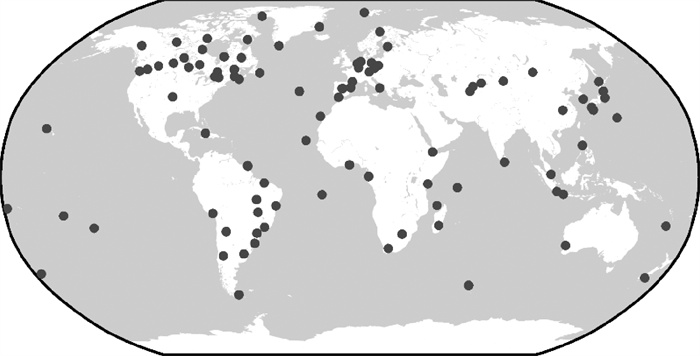
|
| 图 1 选取的105个MGEX测站分布 Fig. 1 Geographical distribution of the selected 105 MGEX tracking stations |
PPP解算采用法国国家空间研究中心(CNES)提供的后处理卫星轨道、整数相位钟产品。使用过程中只需对宽巷模糊度改正其小数偏差,窄巷模糊度不做小数偏差改正。试验采用仿动态PPP解算模式,坐标和接收机钟差参数为白噪声估计,对流层湿延迟采用随机游走过程估计,谱密度取10-8m2/s,载波相位浮点模糊度在连续弧段内为常数,在发生周跳时重新初始化。本文PPP数据处理均在开源GAMP软件[26]上完成,参考坐标选用IGS SINEX周解。具体数据处理策略见表 1。
| 类别 | 描述 |
| 测站数 | 105 |
| 卫星数 | 31颗(GPS) |
| 观测值 | L1、L2双频无电离层组合伪距与载波观测值 |
| 采样间隔/s | 30 |
| 卫星截止高度角/(°) | 7 |
| 观测值定权 | 高度角定权,大于30°为1,小于等于30°为2sinE |
| 估计器 | 卡尔曼滤波 |
| 电离层延迟 | 无电离层组合观测值消除 |
| 对流层延迟 | 干延迟模型改正,湿延迟随机游走过程估计 |
| 对流层梯度 | 东西、南北分量分别估计 |
| 相位缠绕 | 模型改正 |
| 相对论效应 | 模型改正 |
| 萨奈克效应 | 模型改正 |
| 潮汐负荷 | 模型改正 |
| 卫星、接收机天线相位中心改正 | igs14.atx |
| 接收机钟差 | 白噪声估计 |
| 接收机坐标 | 白噪声估计 |
| 相位模糊度 | 每个连续弧段内浮点模糊度为常数估计 |
2.2 PPP收敛速度分析
当PPP解算坐标的东(E)、北(N)、垂向(U)3个方向定位偏差绝对值均小于1dm时,认为滤波收敛。为更清晰地呈现不同PPP解的收敛情况,选取前3h的定位结果成图。图 2为模糊度浮点解、LAMBDA固定解和BIE解68%分位数的定位误差,其计算过程为:以第1个历元为例,将该历元所有测站所有天PPP解取绝对值排序,然后取68%分位数所得,其他历元以此类推。由图 2可以看出,模糊度浮点解收敛最慢,BIE解收敛最快。与模糊度浮点解相比,LAMBDA固定解与BIE解在东、北、垂向3个方向收敛性能均提升显著。相比LAMBDA固定解,BIE解在东、垂向收敛有进一步明显提升,表明BIE法相比LAMBDA固定在PPP收敛阶段更有优势。可以看出,滤波收敛阶段BIE解收敛曲线相比LAMBDA固定解更陡峭。收敛后,当滤波时间在约40min时,BIE解与LAMBDA固定解基本吻合。
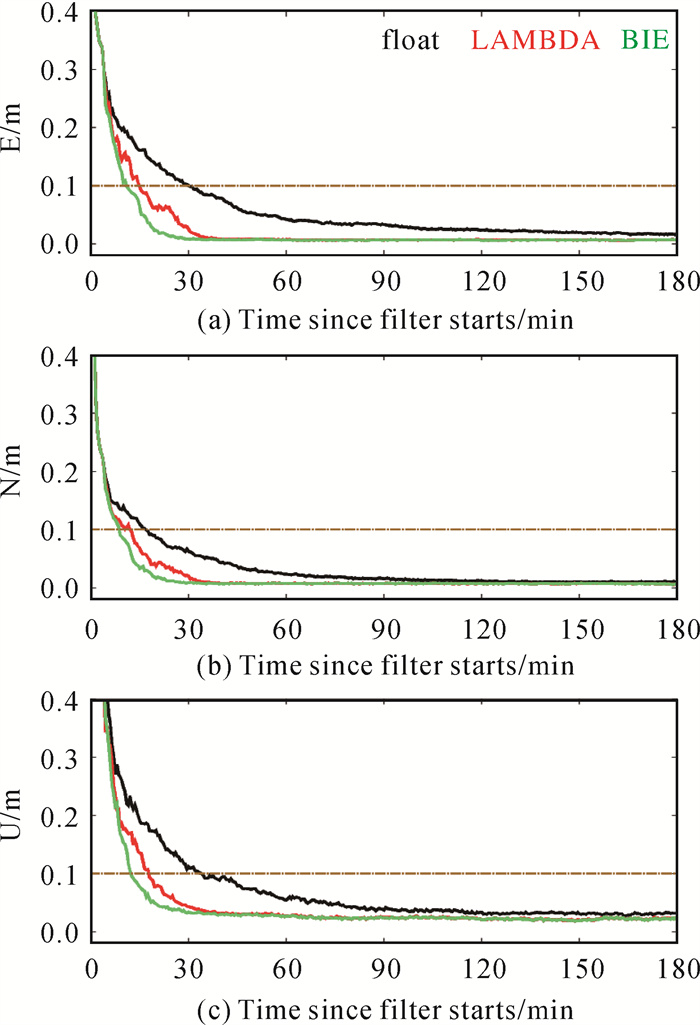
|
| 图 2 3种动态PPP解定位误差(68%分位数) Fig. 2 Positioning errors derived from three kinematic PPP solutions (68% percentile) |
表 2给出了3种动态PPP解收敛时间统计,括号中的百分数指标是相对上一PPP解收敛性能提升百分比,如无特殊说明,图 3与表 3均如此表示。对三维位置来说,GPS浮点解收敛时间基本在35min左右,模糊度固定技术可显著改善PPP收敛时间至20min以内,东、北、垂向收敛时间分别减小了51%、26%和48%。相比LAMBDA固定解,BIE解的3个方向收敛性能可进一步改善37%、28%与31%。
| PPP解 | 东向(E) | 北向(N) | 垂向(U) |
| 浮点解 | 30.5 | 17.0 | 34.5 |
| LAMBDA解 | 15.0(51%) | 12.5(26%) | 18.0(48%) |
| BIE解 | 9.5(37%) | 9.0(28%) | 12.5(31%) |
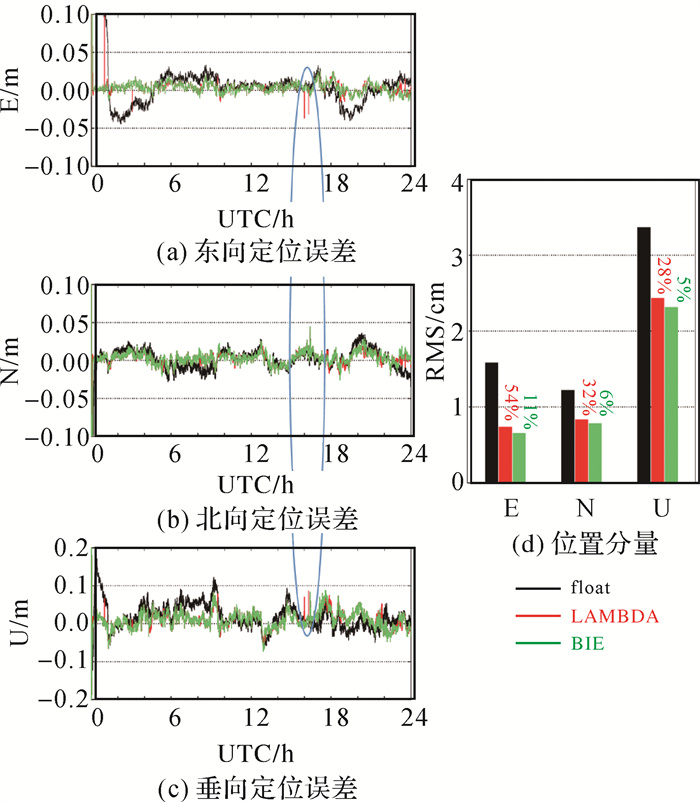
|
| 图 3 3种动态PPP定位误差(2021年DOY 32,测站GMSD) Fig. 3 Positioning errors derived from three kinematic PPP solutions on DOY 32, 2021 at station GMSD |
| PPP解 | 东向(E) | 北向(N) | 垂向(U) |
| float | 1.46 | 1.23 | 3.12 |
| LAMBDA | 0.95(35%) | 0.92(25%) | 2.79(11%) |
| BIE | 0.86(9%) | 0.85(8%) | 2.71(3%) |
2.3 PPP定位精度分析
模糊度固定可靠性一直是GNSS高精度定位面临的难题[27]。在PPP模糊度固定过程中,受到观测数据质量、服务端产品质量等因素影响,模糊度固定错误会导致定位结果出现跳点或者不连续,这也是影响PPP固定解可靠性的关键因素。而BIE通过多个备选整数解加权融合,能够有效抑制由于模糊度固定错误产生的跳点和阶跃,提升PPP定位的连续性和可靠性。为评估BIE解相比LAMBDA固定解在收敛后对定位精度的提升,利用30s观测数据计算给出收敛后PPP浮点解、LAMBDA固定解、BIE解定位情况。图 3为测站GMSD在DOY 32的3种GPS动态定位误差曲线(图 3(a)、(b)、(c))及收敛后的定位精度统计(图 3(d))。在PPP滤波收敛阶段,由于载波相位模糊度精度较低,LAMBDA固定解存在跳跃,而BIE解相对较为稳定;待滤波收敛后,在UTC 17:00—24:00之间,浮点模糊度解坐标序列波动较大,LAMBDA固定解存在固定错误的情况(如图 3中蓝色椭圆圈内所示),导致位置解有跳跃,而BIE解相对稳定一些。从收敛后精度统计柱状图可以看出,BIE解相比LAMBDA解,定位精度进一步有5%~11%的提升。
为充分对比不同PPP动态解收敛后定位精度,选取滤波开始2h后的定位误差用于统计收敛后定位精度[28],利用箱线图来描述定位精度的分布情况,其中上、下边缘线分别表示95%和5%分位数,矩形盒的上、下两端线分别表示75%和25%分位数,矩形盒内部线表示中位数,即50%分位数[29]。图 4给出了所选105个测站一周不同动态PPP解定位精度分布箱线图,表 3列出了相应的中位数统计指标。模糊度固定对东方向精度改善最为明显,LAMBDA固定解相比浮点解提高了35%,进一步地,BIE解精度相比LAMBDA固定解提高了9%。整体来看,BIE解相比LAMBDA固定解有不同程度的精度提高,范围为3%~9%。
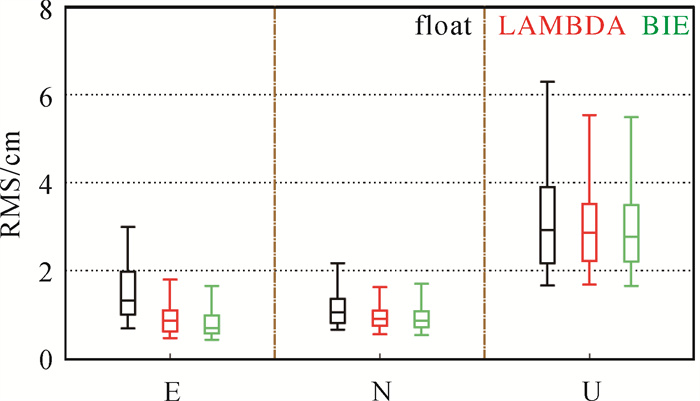
|
| 图 4 3种动态PPP定位精度分布 Fig. 4 Distribution of positioning accuracy derived from three kinematic PPP results |
3 结论
缩短GNSS PPP收敛时间和提升PPP定位精度是目前GNSS高精度定位的关键问题。区别于传统的模糊度浮点解和固定解方案,本文研究发现采用BIE方法可以进一步提升PPP定位性能。BIE方法是采用对多个模糊度整数备选集加权融合来估计模糊度浮点解,该方法能够利用模糊度整数解来提升浮点解估计精度,又避免了模糊度固定错误风险。PPP模糊度估计模型强度相对较弱,并且浮点解残余误差难以准确建模,而BIE解比传统整数解更适合这种弱模型模糊度估计场景。为了验证BIE法在PPP模糊度估计中的效果,本文选取105个全球分布MGEX测站一周30s采样间隔观测数据,从收敛时间和收敛后定位精度分别验证了BIE法相比LAMBDA固定法对PPP定位性能的提升效果。主要结论为:
(1) PPP收敛阶段,浮点模糊度精度较差,LAMBDA固定解存在错误固定、解不够稳定的问题,而BIE解更为稳定。对于收敛性能来说,LAMBDA固定可将单GPS动态PPP收敛时间从模糊度浮点解的40min减小至20min以内,而BIE解可将收敛时间进一步减小至10min左右。
(2) 相比浮点解定位精度,LAMBDA固定解和BIE解均提升明显,BIE解相比LAMBDA固定解可进一步提升3%~9%。
(3) 整体而言,相比模糊度固定解,BIE解对收敛时间有明显改善,对收敛后的定位精度也有一定改善。
| [1] |
MALYS S, JENSEN P A. Geodetic point positioning with GPS carrier beat phase data from the CASA UNO experiment[J]. Geophysical Research Letters, 1990, 17(5): 651-654. DOI:10.1029/GL017i005p00651 |
| [2] |
ZUMBERGE J F, HEFLIN M B, JEFFERSON D C, et al. Precise point positioning for the efficient and robust analysis of GPS data from large networks[J]. Journal of Geophysical Research, 1997, 102(B3): 5005-5017. DOI:10.1029/96JB03860 |
| [3] |
张小红, 李星星, 李盼. GNSS精密单点定位技术及应用进展[J]. 测绘学报, 2017, 46(10): 1399-1407. ZHANG Xiaohong, LI Xingxing, LI Pan. Review of GNSS PPP and its application[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1399-1407. DOI:10.11947/j.AGCS.2017.20170327 |
| [4] |
张小红, 胡家欢, 任晓东. PPP/PPP-RTK新进展与北斗/GNSS PPP定位性能比较[J]. 测绘学报, 2020, 49(9): 1084-1100. ZHANG Xiaohong, HU Jiahua, REN Xiaodong. New progress of PPP/PPP-RTK and positioning performance comparison of BDS/GNSS PPP[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(9): 1084-1100. DOI:10.11947/j.AGCS.2020.20200328 |
| [5] |
杨元喜, 许扬胤, 李金龙, 等. 北斗三号系统进展及性能预测——试验验证数据分析[J]. 中国科学: 地球科学, 2018, 48(5): 584-594. YANG Yuanxi, XU Yangyin, LI Jinlong, et al. Progress and performance evaluation of BeiDou global navigation satellite system: data analysis based on BDS-3 demonstration system[J]. Science China Earth Sciences, 2018, 48(5): 584-594. DOI:10.1360/N072017-00434 |
| [6] |
蔡洪亮, 孟轶男, 耿长江, 等. 北斗三号全球导航卫星系统服务性能评估: 定位导航授时、星基增强、精密单点定位、短报文通信与国际救援[J]. 测绘学报, 2021, 50(4): 427-435. CAI Hongliang, MENG Yinan, GENG Changjiang, et al. BDS-3 performance assessment: PNT, SBAS, PPP, SMC and SAR[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(4): 427-435. DOI:10.11947/j.AGCS.2021.20200549 |
| [7] |
张宝成, 欧吉坤, 袁运斌, 等. 利用非组合精密单点定位技术确定斜向电离层总电子含量和站星差分码偏差[J]. 测绘学报, 2011, 40(4): 447-453. ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Calibration of slant total electron content and satellite-receiver's differential code biases with uncombined precise point positioning technique[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 447-453. |
| [8] |
GE M, GENDT G, ROTHACHER M, et al. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations[J]. Journal of Geodesy, 2008, 82(7): 389-399. DOI:10.1007/s00190-007-0187-4 |
| [9] |
LAURICHESSE D, MERCIER F, BERTHIAS J. Real time precise GPS constellation orbits and clocks estimation using zero-difference integer ambiguity fixing[C]//Proceedings of 2009 ION ITM. California, USA: IEEE, 2009.
|
| [10] |
COLLINS P, BISNATH S, LAHAVE F, et al. Undifferenced GPS ambiguity resolution using the decoupled clock model and ambiguity datum fixing[J]. Navigation, 2010, 57(2): 123-135. DOI:10.1002/j.2161-4296.2010.tb01772.x |
| [11] |
TEUNISSEN P, KHODABANDEH A. Review and principles of PPP-RTK methods[J]. Journal of Geodesy, 2015, 89: 217-240. DOI:10.1007/s00190-014-0771-3 |
| [12] |
李博峰, 葛海波, 沈云中. 无电离层组合、Uofc和非组合精密单点定位观测模型比较[J]. 测绘学报, 2015, 44(7): 734-740. LI Bofeng, GE Haibo, SHEN Yunzhong. Comparison of ionosphere-free, Uofc and uncombined PPP observation models[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7): 734-740. DOI:10.11947/j.AGCS.2015.20140161 |
| [13] |
耿江辉, 常华, 郭将, 等. 面向城市复杂环境的3种多频多系统GNSS单点高精度定位方法及性能分析[J]. 测绘学报, 2020, 49(1): 1-13. GENG Jianghui, CHANG Hua, GUO Jiang, et al. Three multi-frequency and multi-system GNSS high-precision point positioning methods and their performance in complex urban environment[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(1): 1-13. DOI:10.11947/j.AGCS.2020.20190106 |
| [14] |
VERHAGEN S. Integer ambiguity validation: an open problem?[J]. GPS Solutions, 2004, 8(1): 36-43. DOI:10.1007/s10291-004-0087-5 |
| [15] |
LI Pan, ZHANG Xiaohong, REN Xiaodong, et al. Generating GPS satellite fractional cycle bias for ambiguity-fixed precise point positioning[J]. GPS Solutions, 2016, 20: 771-782. DOI:10.1007/s10291-015-0483-z |
| [16] |
TEUNISSEN P. Theory of integer equivariant estimation with application to GNSS[J]. Journal of Geodesy, 2003, 77(7-8): 402-410. DOI:10.1007/s00190-003-0344-3 |
| [17] |
TEUNISSEN P. Best integer equivariant estimation for elliptically contoured distributions[J]. Journal of Geodesy, 2020, 94: 82. DOI:10.1007/s00190-020-01407-2 |
| [18] |
WEN Z, HENKEL P, BRACK A, et al. Best integer equivariant estimation for precise point positioning[C]//Proceedings of the 54th International Symposium. Zadar, Croatia: [s. n. ], 2012: 279-282.
|
| [19] |
DUONG V, HARIMA K, CHOY S, et al. GNSS best integer equivariant estimation using multivariant t-distribution: a case study for precise point positioning[J]. Journal of Geodesy, 2021(95): 10. DOI:10.1007/s00190-020-01461-w |
| [20] |
WANG Lei, VERHAGEN S. A new ambiguity acceptance test threshold determination method with controllable failure rate[J]. Journal of Geodesy, 2015, 89(4): 361-375. DOI:10.1007/s00190-014-0780-2 |
| [21] |
TEUNISSEN P. On the computation of the best integer equivariant estimator[J]. Artificial Satellites, 2005, 40(3): 161-171. |
| [22] |
李博峰, 沈云中, 张兴福. 纳伪概率可控的四舍五入法及其在RTK模糊度固定中的应用[J]. 测绘学报, 2012, 41(4): 483-489. LI Bofeng, SHEN Yunzhong, ZHAGN Xingfu. Error probability controllable integer rounding method and its application to RTK ambiguity resolution[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 483-489. |
| [23] |
ODOLINSKI R, TEUNISSEN P. Best integer equivariant estimation: performance analysis using real data collected by low-cost, single-and dual-frequency, multi-GNSS receivers for short-to long-baseline RTK positioning[J]. Journal of Geodesy, 2020, 94: 91. DOI:10.1007/s00190-020-01423-2 |
| [24] |
周锋, 徐天河. GPS/BDS/Galileo三频精密单点定位模型及性能分析[J]. 测绘学报, 2021, 50(1): 61-67. ZHOU Feng, XU Tianhe. Modeling and assessment of GPS/BDS/Galileo triple-frequency precise point positioning[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(1): 61-67. DOI:10.11947/j.AGCS.2021.20200146 |
| [25] |
WANG Lei, FENG Yanming, GUO Jiming, et al. Impact of decorrelation on success rate bounds of ambiguity estimation[J]. Journal of Navigation, 2016, 69(5): 1061-1081. DOI:10.1017/S0373463316000047 |
| [26] |
ZHOU Feng, DONG Danan, LI Weiwei, et al. GAMP: an open-source software of multi-GNSS precise point positioning using undifferenced and uncombined observations[J]. GPS Solutions, 2018, 22: 33. DOI:10.1007/s10291-018-0699-9 |
| [27] |
WANG Lei, FENG Yanming, GUO Jiming. Reliability control of single-epoch RTK ambiguity resolution[J]. GPS Solutions, 2017, 21(2): 591-604. DOI:10.1007/s10291-016-0550-0 |
| [28] |
ZHOU Feng, DONG Danan, GE Maorong, et al. Simultaneous estimation of GLONASS pseudorange inter-frequency biases in precise point positioning using undifferenced and uncombined observations[J]. GPS Solutions, 2018, 22: 19. DOI:10.1007/s10291-017-0685-7 |
| [29] |
ZHOU Feng, CAO Xinyun, GE Yulong, et al. Assessment of the positioning performance and tropospheric delay retrieval with precise point positioning using products from different analysis centers[J]. GPS Solutions, 2020, 24: 12. DOI:10.1007/s10291-019-0925-0 |



