2. 武汉大学卫星导航定位技术研究中心, 湖北 武汉 430079;
3. 地理信息工程国家重点试验室, 陕西 西安 710054;
4. 西部矿产资源与地质工程教育部重点试验室, 陕西 西安 710054
2. GNSS Research Center, Wuhan University, Wuhan 430079, China;
3. State Key Laboratory of Geographic Information Engineering, Xi'an 710054, China;
4. Key Laboratory of Western China's Mineral Resources and Geological Engineering, Ministry of Education, Xi'an 710054, ChinaAbstract
目前,基于载波相位的实时动态差分(RTK)和实时精密单点定位(RT-PPP)技术是GNSS实时高精度导航定位应用中最为常见的两种技术。RTK面临的主要问题是,随着基线距离的增长,大气误差相关性降低,网络RTK技术利用多个区域参考站数据,在参考站基线模糊度固定后通过大气延迟误差建模可满足大范围终端用户实时快速高精度定位需求。精密单点定位(precise point positioning, PPP)技术具有无须依赖密集参考站网、作业灵活、无作业范围限制的优点,能够直接获得国际地球参考框架下的高精度位置坐标[1-3],该技术在智能交通、精密农业、海洋资源勘探等诸多领域有着广阔的应用前景[4-5]。
相比RTK技术,PPP在实时应用中还相对较少,主要原因是该技术需额外依赖高可靠的精密轨道钟差及硬件延迟产品且收敛时间较长。近年来,研究表明模糊度固定可以缩短PPP的收敛时间并提高定位精度[6-9]。PPP模糊度固定的前提是提供高精度的整数钟/UPD产品[10-12]。在实时应用中,受参数估计策略、数据质量控制难度大等因素的影响,实时轨道不如事后轨道稳定且误差相对较大[13],GNSS终端PPP使用全球统一的整数钟/UPD时受轨道残余误差影响模糊度固定可靠性难以保证[14-15]。文献[16]研究了基于区域参考站网的整数钟估计方法,其研究结果表明相比法国太空研究中心(CNES)提供的全球整数钟/相位偏差改正产品,PPP用户采用区域整数钟产品可以有效补偿实时轨道误差并显著提高用户的收敛速度及定位精度。
模糊度固定虽然可以在一定程度上加快PPP用户坐标的收敛速度,但是模糊度固定仍需15~30 min的时间[6, 17],难以有效提高GNSS高精度用户的作业效率。为了加快定位用户的初始化速度,文献[18]提出了PPP-RTK的概念,该方法借鉴常规网络RTK大气延迟误差改正的思路,在参考站非差模糊度固定的基础上,利用附近基准站的大气延迟内插用户处的大气误差改正数,进而加快PPP用户的模糊度固定速度[19-20]。文献[21—22]提出了一种新的PPP-RTK参考站网处理方案,通过S变换直接估计卫星钟差、相位偏差、模糊度及大气等参数,可同时满足区域参考网内单双频PPP-RTK用户快速初始化需求[23]。与网络RTK技术相比,PPP-RTK技术具有数据播发量小、不依赖密集参考站网等理论优势,但在服务性能方面该技术与网络RTK技术的对比论证尚不充分。
实际上,基于参考站非差固定解提取的大气延迟在参考站间做差后可以得到基线的双差大气延迟,因此区域参考站辅助的非差网络RTK可以兼容双差网络RTK模式,进而同时支持覆盖区域范围内的PPP以及RTK用户的快速模糊度固定。理论上,在参考站的密度一致时,非差网络模式和双差网络RTK模式下的用户初始化速度和定位精度相当,然而非差和双差模型的误差影响因素不同,在实际应用中服务端生成轨道钟差、硬件延迟及大气等产品时需顾及不同类型用户的误差特点。另外,不同服务模式下终端用户使用大气延迟的方法也不尽相同,定位结果可能也有一定差异,因此有必要对基于区域参考站网的PPP及RTK的一体化服务方法及其服务效果展开深入研究。
本文首先在介绍非差模糊度固定的基础上给出了服务于PPP和RTK用户的区域整数钟/UPD、非差大气延迟及虚拟参考站观测值(VRS)生成方法,然后基于西北某省的CORS网数据详细对比分析了区域参考站网辅助下的PPP和RTK定位效果。本文的相关分析结果可为区域GNSS参考站网实时高精度服务应用提供参考。
1 区域参考站网非差模糊度固定方法参考站模糊度固定是解算高精度服务产品的前提,GNSS伪距和相位观测值的基本观测方程可以表示为
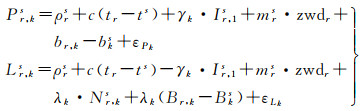 (1)
(1)
式中,P和L分别表示伪距和相位观测值;ρ表示卫星s到接收机r之间的几何距离;tr和ts分别表示接收机和卫星钟差;c表示光速;k表示信号频点;Ir, 1s表示1号频点卫星s的斜路径电离层延迟;γk表示与频率相关的电离层延迟系数,γk=f12/fk2;zwd和m分别表示天顶对流层延迟和对应的映射函数;N为整周模糊度;λ为波长;br, k和bks分别为接收机端和卫星端的伪距硬件延迟;Br, k和Bks分别为接收机端和卫星端的相位硬件延迟;εLk和εPk分别表示相位和伪距的观测值噪声。
参考站网的模糊度固定策略可采用先宽巷后窄巷的方法[10],其中宽巷模糊度的浮点解Nr, WLs基于双频HMW组合观测值平滑解算[24-25]
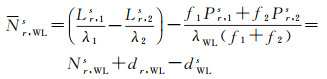 (2)
(2)
式中,Nr, WLs表示宽巷模糊度的整数部分;dWLs和dr, WL是卫星和接收机端的宽巷UPD。
由于参考站坐标已知,无电离层组合浮点解PPP的伪距和相位观测方程可表示为
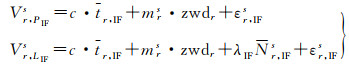 (3)
(3)
式中,Vr, PIFs和Vr, LIFs分别表示伪距和载波相位观测值的残差,扣除了用精密轨道和基准站坐标计算的几何距离、精密浮点钟差、对流层干延迟、天线PCO和PCV[26]、相位缠绕误差[27]和潮汐误差等;浮点模糊度Nr, IFs和接收机钟差tr, IF均为吸收伪距和相位硬件延迟后的表达形式。基于式(3)采用卡尔曼滤波即可解算无电离层浮点模糊度Nr, IFs。窄巷浮点模糊度Nr, NLs可用该模糊度扣除固定后的宽巷模糊度得到[10, 25]
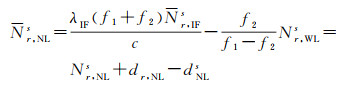 (4)
(4)
式中,Nr, NLs表示窄巷模糊度的整数部分;dNLs和dr, NL分别为卫星和接收机端的窄巷UPD。
为了恢复非差模糊度的整数特性,需改正卫星端和接收机端的UPD,对于服务端来讲,关键是分离式(2)和式(4)中整周模糊度和UPD参数。假设本文试验有m个测站共跟踪了n颗卫星,接收机和卫星端的UPD可按式(5)求解
 (5)
(5)
式中,Cn=[Cn1Cn2…Cnm]T,是测站n的浮点模糊度向量;Nn=[Nn1Nn2…Nnm]T,是对应的整周模糊度;dr=[d1d2…dm],是接收机端UPD向量;ds=[d1d2…dn],是卫星端UPD向量;R和S是dr和ds对应的系数矩阵。上述方程秩亏,需要添加一个基准,可以选取某颗卫星或接收机的基准小数偏差为0[28]。由式(5)可知,确定UPD参数实际上是一个迭代过程,一方面UPD的解算依赖整周模糊度固定,另一方面整周模糊度的确定需要消除UPD的影响,具体解算过程可参考文献[8, 11, 29—30]。迭代过程的终止条件是相邻计算的UPD小于某个阈值(如0.01周)。为了确保模糊度确定的可靠性,最终固定的整周模糊度需通过模糊度偏差及成功率检核
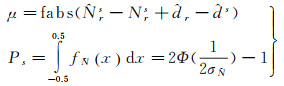 (6)
(6)
式中,fabs表示取绝对值;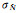
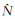
除了UPD方法,另一种恢复非差模糊度整数特性的方法是整数钟方法[11]。尽管两种方法理论上等价[31-32],但在考虑实时轨道误差的影响时,两种方法有所差异,模糊度参数是作为常量参数估计的,因此UPD方法中从浮点模糊度分离的窄巷UPD产品吸收的轨道误差具有滞后性,而整数钟方法是在模糊度确定后更新钟差参数,由于钟差是作为白噪声参数估计,可更好地吸收当前历元实时轨道误差。区域范围内参考站受轨道误差的影响具有一致性,钟差参数可以较好补偿实时轨道误差[33-34]。为此,本文在参考站模糊度固定后进一步解算区域卫星钟差。
钟差估计一般采用无电离层组合模型,利用多个站的载波和伪距观测值数据同时估计接收机钟差、卫星钟差、对流层及模糊度参数
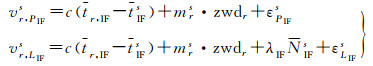 (7)
(7)
式中,tIFs是浮点解钟差,和IGS提供的钟差基准保持一致。将上一节通过模糊度检核的参考站宽巷模糊度NWL和窄巷模糊度NNL转换为无电离层组合模糊度后,作为虚拟方程添加到非差钟差估计模型中
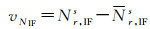 (8)
(8)
式中,Nr, IFs是无电离层组合固定解模糊度,表达式如下
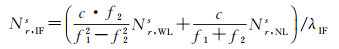 (9)
(9)
式(8)中,模糊度是外部高精度约束,需给一个很小的方差,如10-6。基于式(7)和式(8)进行参数估计时,模糊度参数中与卫星相关的硬件延迟(窄巷UPD)会转移到卫星钟差参数,模糊度参数中和接收机相关的硬件延迟会转移到接收机钟差参数。此时,非差钟差估计模型中的卫星和接收机钟差参数的表现形式如下
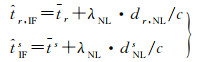 (10)
(10)
式中,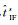
为了方便终端用户使用,可将整数钟转换为窄巷UPD,并结合已解算的宽巷UPD生成每个频点相位观测值所需的硬件延迟偏差改正,公式如下
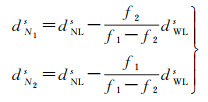 (11)
(11)
式中,dNLs是基于整数钟和浮点钟差转换的,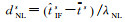
在非差模糊度固定后,利用色散误差与频率相关的特性可以分别计算每颗卫星的对流层误差(非色散误差)和电离层误差(色散误差)
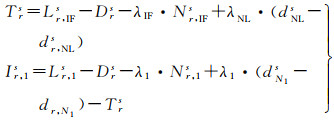 (12)
(12)
式中,T为斜路径对流层误差;D为其他非色散项之和,包括卫星和接收机间的几何距离、卫星钟差、接收机钟差等。在得到区域范围内各个参考站的非差对流层和电离层延迟后,为了削弱接收机钟差、UPD等产品误差对大气延迟建模的影响,可将区域内的参考站进行Delaunay三角形构网,提取每条基线的双差大气延迟后基于常用的线性内插方法进行建模[35]
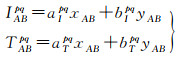 (13)
(13)
式中,xAB=xB-xA;yAB=yB-yA;(xA, yA)、(xB, yB)分别为A与B测站高斯投影下的平面坐标;a、b为大气模型系数;p表示参考卫星。需要说明的是,对流层延迟与测站高度具有较强的相关性,参考站间高差较大时可采用先验高精度对流层模型将基线的对流层归化到统一的高程面后再建模[36-37]。利用区域内的基线大气延迟信息分别对每颗非参考卫星q分别进行建模
 (14)
(14)
式中,n表示区域内参与建模的基线数,基于式(14)即可通过最小二乘即可获得每颗卫星的电离层和对流层建模系数。
对于网络RTK,目前使用最为广泛的是VRS技术,生成VRS观测值时,需要在区域范围内选取一个主参考站,一般选取离用户处概略坐标最近的CORS站作为主参考站,然后根据大气建模系数内插各颗卫星的电离层与对流层延迟,公式如下
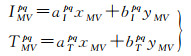 (15)
(15)
式中,M和V分别代表主参考站和虚拟参考站,在内插得到每颗卫星的用户位置与主参考站的双差大气延迟后,即可根据主参考站的观测值生成终端用户概略坐标位置的虚拟观测值,公式如下
 (16)
(16)
式(16)是基于以下假设生成的:①虚拟参考站参考星的电离层和对流层延迟与主参考站相同;②虚拟参考站与主参考站的接收机钟差相同;③虚拟参考站与主参考站所有卫星的相位观测值的模糊度相同。
对于用于PPP-RTK的非差大气生成方法,终端用户处各颗卫星的电离层延迟可直接利用双差电离层延迟IMVpq和主参考站的非差大气延迟得到
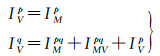 (17)
(17)
式中,假设用户参考星的电离层延迟和主参考站相同,会带来额外的偏差,但是由于所有卫星的偏差是一致的,该偏差会被接收机钟差参数吸收,因而不会影响PPP用户的定位精度。
由于PPP终端用户定位模型估计的是天顶方向对流层延迟,因此服务端需提供对应天顶对流层延迟信息作为约束。天顶对流层建模的过程和双差大气建模类似,提取每条基线的相对天顶对流层
 (18)
(18)
类似于式(14),利用区域内的多条基线进行线性内插建模
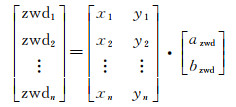 (19)
(19)
在得到天顶对流层的区域建模系数后,即可根据主考站的对流层延迟zwdM计算终端用户所需的天顶对流层延迟
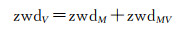 (20)
(20)
式中,zwdMV=azwdxMV+bzwdyMV,为内插的终端用户近似位置与主参考站间的相对天顶对流层延迟。
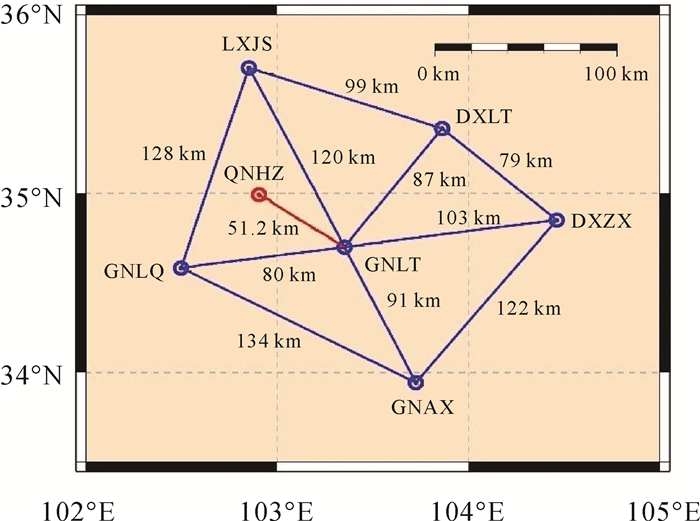
3 PPP和RTK终端用户的快速定位验证分析 3.1 试验数据及处理策略为了验证基于区域参考站网的PPP和RTK定位效果并进行对比分析,试验收集了西北某省2017年1月15日—2017年1月16日的CORS站数据,如图 1所示,一共7个GNSS站点,其中6个站点(蓝色圆圈)作为参考站,用于计算区域整数钟差和大气改正等信息,另外1个站点GNHZ作为终端用户(红色圆圈),用于测试PPP-RTK和网络RTK终端的定位效果。根据Delaunay构网规则,6个参考站共形成10条基线,平均站间距为104.3 km,与终端用户GNHZ距离最近的参考站是GNLT站,GNHZ-GNLT基线距离为52.1 km。所有的接收机型号均为TRIMBLE NETR9,天线型号为TRM59900.00,接收机同时支持GPS/BDS系统,数据采样率为30 s。
|
| 注:蓝色圆圈为参考站,红色圆圈为终端用户。 图 1 参考站及终端用户位置分布 Fig. 1 Distribution of reference and terminal user stations |
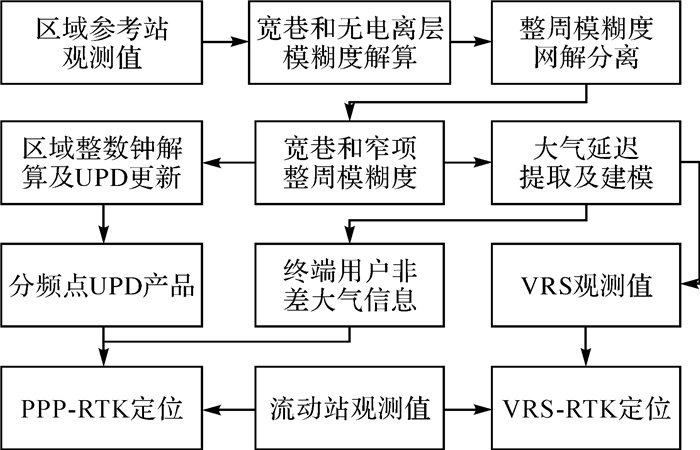
图 2展示了基于区域参考站网的PPP和网络RTK一体化服务数据处理流程,基于CNES提供的实时精密轨道钟差产品服务端首先解算区域参考站网每个GNSS站的宽巷和无电离层组合浮点模糊度,同时采用网解模式分离浮点模糊度的整数部分和硬件延迟小数部分进而固定宽巷和窄项模糊度;然后在模糊度固定解的基础上解算区域整数钟并更新得到相位观测值各个频点所需的UPD产品,同时提取大气延迟建模并根据终端用户的近似坐标生成虚拟参考站观测值(VRS)及非差大气延迟;最后,终端用户基于采集的数据及服务端生成的产品分别采用PPP和RTK模式进行定位。
|
| 图 2 基于区域参考站网的PPP和RTK一体化服务数据处理流程 Fig. 2 Data processing flowchart of PPP & RTK integrated service method |
对于RTK用户,区域参考站网处理生成的产品主要是虚拟参考站观测值,终端用户接收到的虚拟参考站坐标和自身位置很近,在进行RTK定位时通常忽略大气延迟,此种定位方式称作VRS-RTK。对于PPP用户,在利用全球轨道钟差的基础上,基于区域参考站网处理生成的分频点UPD、非差斜路径电离层延迟和天顶对流层延迟产品进行定位,大气延迟一般作为虚拟观测值信息加快PPP定位的初始化速度,此种定位方式称作PPP-RTK,本文将未使用外部大气信息的PPP固定解定位模式称作PPP-AR。大气虚拟观测方程如下
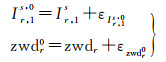 (21)
(21)
式中,虚拟观测值Ir, 1s, 0和zwdr0是内插得到终端用户的斜路径电离层和天顶湿分量延迟,其对应的随机模型分别为σIr, 1s, 02和σ2zwdr0;Ir, 1s和zwdr表示终端用户电离层和天顶湿分量延迟估计参数;ε表示内插大气延迟与估计大气的偏差;σ2表示区域大气建模内插值的方差。表 1给出了VRS-RTK和PPP-RTK两种终端定位模式的数据处理策略。本文在数据处理时均采用存储数据基于卡尔曼滤波仿实时处理,钟差轨道采用CNES存储的实时产品(http://www.ppp-wizard.net/products/REAL_TIME/)。
| 终端定位模式 | VRS-RTK | PPP-RTK |
| 观测值 | 非组合双差 | 非差非组合 |
| 硬件延迟改正 | 无 | UPD改正 |
| 对流层延迟 | 忽略 | 估计天顶湿分量+虚拟观测值 |
| 电离层 | 忽略 | 估计斜路径电离层+虚拟观测值 |
| 模糊度 | 估计 | 估计 |
| 坐标 | 估计 | 估计 |
3.2 大气延迟建模精度分析
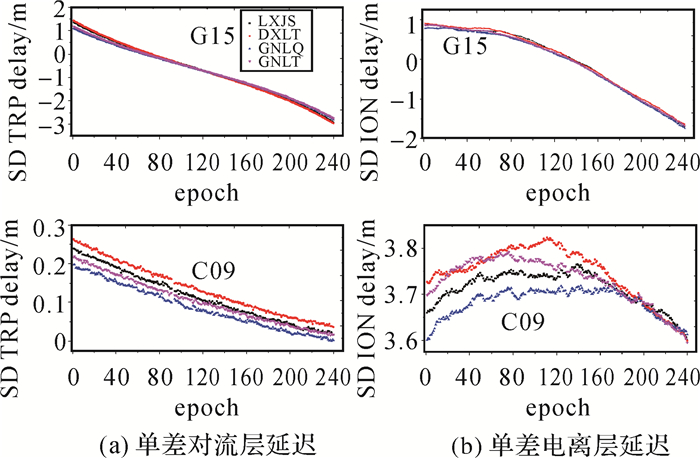
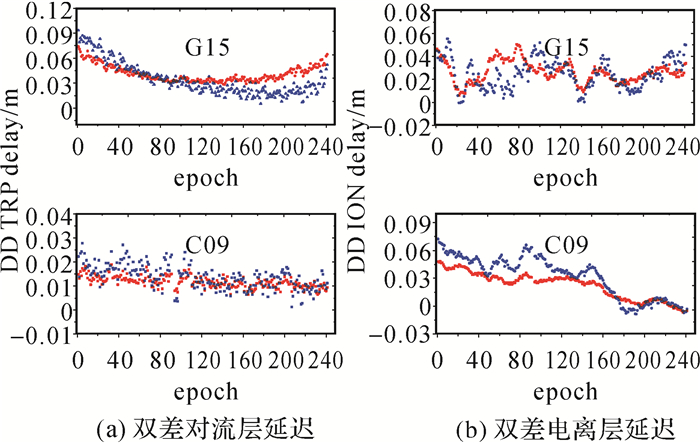
考虑到大气误差的空间相关性,内插某一未知点大气延迟时通常是基于其临近参考站的大气信息,本文选取距离内插点不超过80 km的参考站所构成的基线进行建模。在内插终端用户GNHZ处大气信息时,共选取了4个参考站(LXJS、GNLQ、GNLT和DXLT),4个参考站共形成了5条基线。图 3是4个参考站基于PPP固定解提取两颗卫星的星间单差电离层和对流层延迟结果(时长2 h),GPS的参考星是G02,BDS的参考星是C06。通过单差处理,与接收机相关的偏差已消除,4个参考站提取的大气延迟较为接近。C09卫星的对流层和电离层延迟在2 h内的变化约为0.3和0.2 m,而G15卫星的对流层延迟和电离层延迟在2 h内的变化达到了4 m和2.5 m,主要原因是在这段时间内G15卫星的高度角变化范围大(32.7°, 85.8°),而C09卫星的高度角变化范围小(62.9°, 67.9°)。图 4给出了GNHZ-GNLT基线两颗星的大气模型内插值和真值结果,其中真值是将终端用户GNHZ作为参考站计算的。从图 4中可以看出,区域站大气内插精度相对较高,此段时间这两颗卫星的电离层和对流层建模误差均在2 cm左右。
|
| 图 3 参考站模糊度固定解下的单差对流层延迟和电离层延迟 Fig. 3 The single-differenced tropospheric and ionospheric-delay derived from ambiguity-fixed solution |
|
| 注:红色为建模值,蓝色为参考值。 图 4 GNHZ-GNLT模型内插大气延迟与大气延迟真值比较 Fig. 4 Comparison of interpolated and reference atmosphere delay for GNHZ-GNLT baseline |
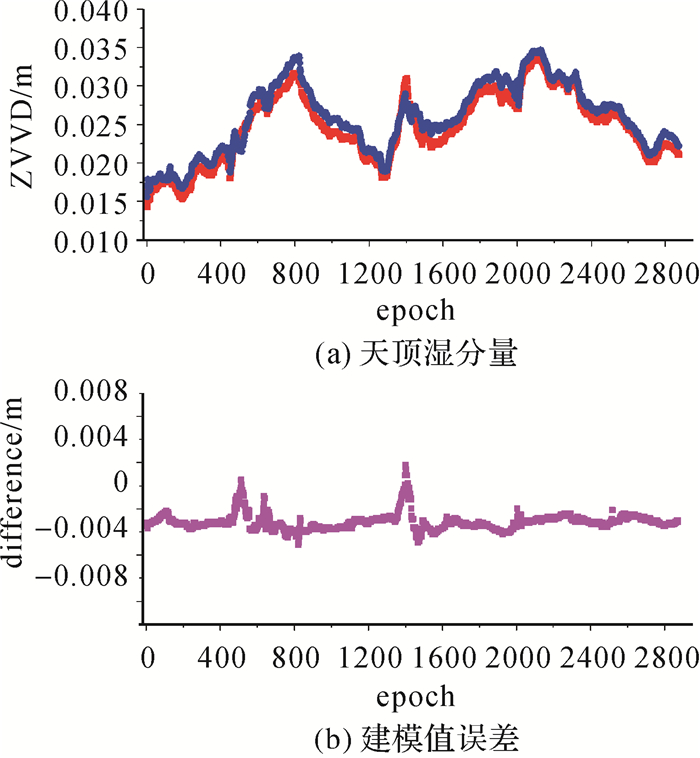
对于VRS-RTK模式,在内插得到GNHZ-GNLT基线的大气延迟后即可根据式(16)得到终端用户近似坐标处的虚拟观测值信息。对于PPP-RTK模式,终端用户GNHZ处的电离层延迟可根据式(17)转换得到,而天顶对流层延迟信息需根据参考站解算的对流层延迟信息内插得到,图 5给出了GNHZ站的天顶湿分量内插值与真值比较结果,由图 5可以看出,对流层天顶方向的内插精度较高,一般不超过4 mm。
|
| 注:红色为建模值,蓝色为真值。 图 5 天顶湿分量模型内插值与真值比较 Fig. 5 Comparison of interpolated and reference zenith troposphere delay |
3.3 基于参考站网的PPP和RTK定位验证分析
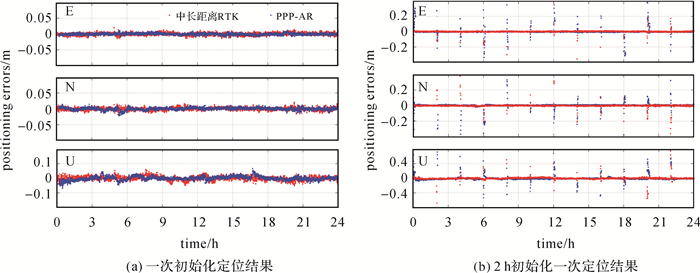
为了提高模糊度固定率,本文采用部分模糊度固定方法,首先将原始的模糊度(L1/L2或者B1/B2)转换为宽巷和窄巷模糊度[38-39],同时根据误差传播定律得到宽巷和窄巷模糊度的方差协方差阵。然后使用LAMBDA方法分别固定宽巷和窄巷模糊度,当宽巷模糊度固定后,再尝试固定窄巷模糊度。为了尽可能获得可靠的模糊度固定解,本文使用基于失败率的模糊度检验方法[40],模糊度固定的失败率设置为1%,如果模糊检验失败,则基于最优解与次最优解是否相等的方法选取模糊度子集并尝试模糊度固定[41],为了确保固定解的定位精度,窄巷模糊度固定的最小数目设置为5颗。图 6是GNHZ站基于图 2方法处理得到UPD产品的GPS/BDS非差非组合PPP-AR和中长距离RTK动态定位误差结果(图 6(b)是每2 h初始化一次的结果),中长距离RTK以最近的GNLT为参考站,两种定位模式均需估计斜路径电离层和天顶对流层延迟(无任何外部大气约束)。PPP-AR和中长距离RTK固定解精度相当(两种定位模式ENU方向的定位误差RMS分别为0.31、0.41、1.36 m和0.36、0.42、1.34 cm),PPP-AR模式固定解水平方向的精度优于0.5 cm, 这主要得益于区域整数钟可以较好地补偿CNES实时轨道误差的影响。PPP-AR和RTK 12个时段平均初始化时间分别为10.0和3.5 min,相比中长距离RTK,PPP-AR模式初始化时间仍较长,主要原因是非差PPP模型受电离层及对流层延迟的影响更为显著,参数收敛时间较长。
|
| 图 6 GNHZ站PPP-AR和中长距离RTK定位结果 Fig. 6 Positioning results of PPP and medium-long baseline RTK for GNHZ station |
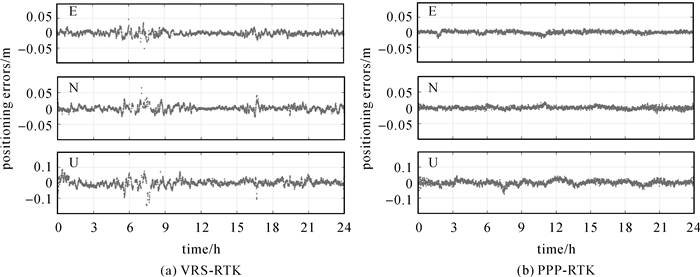
采用上述参考站提取大气延迟并生成GNHZ站近似坐标的VRS观测值,终端用户VRS-RTK定位方式处理得到GNHZ站固定解的坐标结果如图 7(a)所示。VRS-RTK定位ENU方向的RMS统计结果分别为0.74、0.82、2.41 cm,相比中长距离RTK定位精度明显下降,此外,从图中可以看出VRS-RTK在GPS时5∶00—9∶00(地方时13∶00—17∶00)定位精度稍差,且部分历元模糊度无法固定,主要原因是这段时间电离层相对活跃,电离层建模精度差。图 7(b)是GNHZ站在利用大气增强信息的PPP-RTK定位结果,电离层和天顶对流层虚拟观测值是根据周围4个参考站固定解大气信息内插得到,其中天顶对流层方差设置为16 mm2, 电离层延迟方差设置为σ2/sin2el,σ=2 cm。由图 7可以看出,利用区域整数钟转换的UPD产品及区域非差大气的PPP-RTK定位精度仍较高,ENU 3个方向定位误差的RMS统计结果分别为0.33、0.44、1.38 cm,明显好于VRS-RTK的定位结果,主要原因是VRS模式下定位误差中直接包含了大气延迟建模误差的影响,建模误差较大时VRS-RTK定位模糊度固定困难并且定位误差大;而PPP-RTK模式将大气延迟作为参数估计,并引入建模先验信息,参数估计残差小于建模误差因此定位精度高。
|
| 图 7 VRS-RTK和PPP-RTK模式下GNHZ终端用户的定位结果 Fig. 7 Positioning results of VRS-RTK and PPP-RTK for GNHZ station |
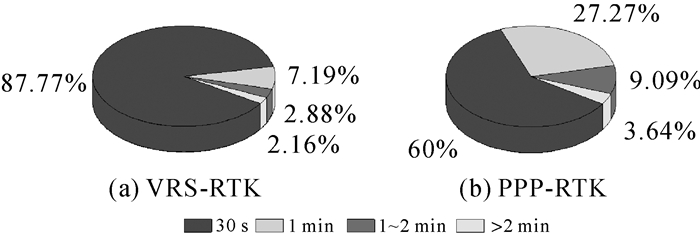
对于实时高精度定位,除了定位精度,另一项重要的评价指标是首次固定时间(TTFF),采用多次初始化的方式进行处理(每10 min初始化一次),每种模式得到144个采样点的结果。VRS模式下144个时段的首次固定时间统计结果如图 8(a)所示,由于所使用的数据采样率为30 s,因此,最快固定时间为30 s。由图 8可以看出,VRS模式下87.8%的时段在单历元即可得到固定解。图 8(b)是大气增强下的PPP-RTK定位首次固定时间统计结果。PPP-RTK模式下,60%的时段单历元即可得到固定解,96.4%的时段数在2 min内完成初始化,相比无大气约束下的PPP-AR定位模式(图 6中GNHZ站首次固定时间约10 min),首次固定时间明显缩短。
|
| 图 8 VRS-RTK和PPP-RTK定位模式下首次固定时间百分比统计结果 Fig. 8 The initialization time statistics results based on VRS-RTK and PPP-RTK positioning mode |
由以上分析可以看出,VRS模式下由于内插的大气信息直接用于观测值改正,RTK终端定位等价于大气强约束,会引入大气建模误差,因此定位精度可能会降低,但其优点是初始化速度快。为了保证VRS模式服务的可靠性,需要确保大气建模的精度,因此对参考站站间距要求较高,站间距不宜过长[35, 42]。
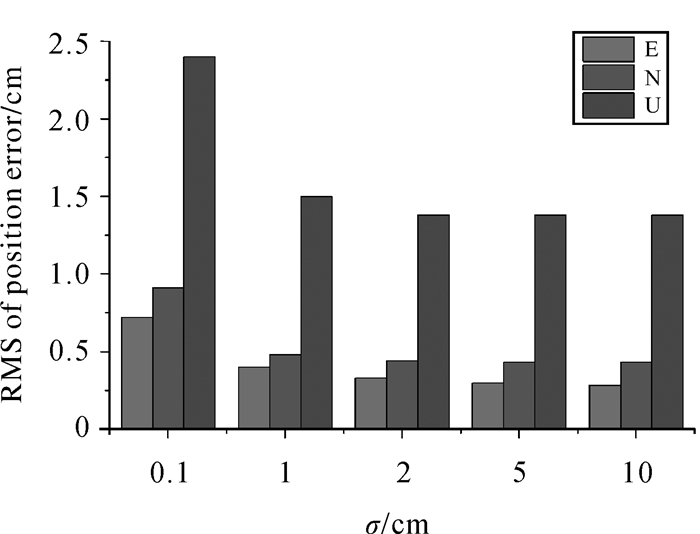
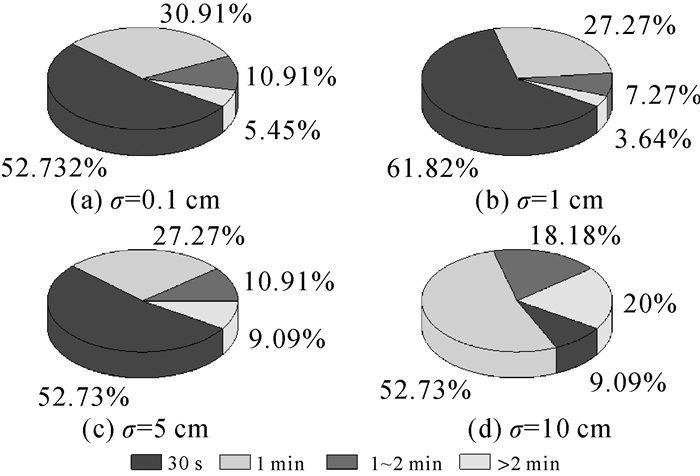
对于PPP-RTK定位,引入区域大气建模信息后收敛速度明显加快。需要注意的是,在引入外部大气约束信息时,对应的随机模型(方差/标准差)不宜过小,如果方差过小,大气建模误差会直接被坐标参数及模糊度参数吸收,从而降低模糊度的固定率及定位精度(如VRS模式),如果方差过大,增强效果会不明显。图 9是不同电离层约束标准下定位误差RMS统计结果,σ在设置为0.1、1、2、5和10 cm时,三维方向的定位精度分别为2.67、1.62、1.49、1.48和1.47 cm。当σ=0.1 cm时,定位误差明显增大;当σ≥2 cm时,定位精度基本相当。图 10是不同电离层标准差下首次固定时间统计结果,结合图 8(σ=2 cm)可以看出, σ在设置为0.1、1、2、5和10 cm时,两分钟内固定的百分比分别是94.5、96.4、96.4、90.9和80%,当σ=1 cm,首次固定时间最短,约89%的时段在两个历元(1 min)内得到固定解。结合固定解精度统计结果可以看出,电离层约束标准差在适当范围内(如1、2 cm)可同时兼顾固定解精度和初始化速度,为了确保定位精度,在实际应用中可以适当放大外部大气约束信息的方差。
|
| 图 9 不同电离层延迟标准下的PPP-RTK定位精度RMS统计结果 Fig. 9 RMS statistical results of PPP-RTK positioning under different prior ionospheric delay variances |
|
| 图 10 不同电离层延迟标准差下的PPP-RTK首次固定时间百分比统计结果 Fig. 10 The initialization time statistics results of PPP-RTK positioning under different prior ionospheric delay variances |
4 总结与讨论
本文在参考站模糊度固定的基础上,实现了基于区域参考站网非差大气信息的PPP及RTK的一体化服务模式,并对两种技术体制下的终端定位性能进行了评估和对比分析。基于平均站间距约为100 km的区域参考站网生成的整数钟/UPD、电离层对流层改正数及VRS等产品对两种终端用户的定位性能进行测试分析,主要得出以下结论:
(1) 区域参考站网估计的整数钟能够较好地补偿实时轨道误差的影响,采用区域整数钟转换的UPD产品进行PPP-AR的定位精度和中长距离RTK相当,水平方向的定位精度可达0.5 cm。PPP-AR和中长距离RTK平均初始化时间分别为10.0和3.5 min,相比RTK,PPP-AR定位所需初始化时间更长。
(2) 参考站网提供的大气信息可以显著提升终端定位用户的初始化速度,对于PPP-RTK和VRS-RTK用户,60.0%和87.7%的时段单历元即可得到固定解,相比PPP-RTK,VRS-RTK的初始化速度更快。基于VRS模式的RTK定位等价于大气强约束,在大气建模误差较大时终端定位精度会显著下降,而PPP-RTK模式将大气延迟作为参数估计并引入先验建模信息,参数估计残差小于建模误差,定位精度仍较高。PPP-RTK和VRS-RTK定位固定解E、N、U 3个方向的RMS分别为0.33、0.44、1.38 cm和0.74、0.82、2.41 cm。
(3) 为了保障VRS服务模式的可靠性,需要确保大气建模的精度,因此对参考站网密度要求较高,而PPP-RTK模式能够顾及大气建模误差的影响,对参考站网尺度具有更强的适应性,其难点是提供与大气建模误差相匹配的精度信息。PPP-RTK模式下电离层约束标准差为0.1、1、2、5、10 cm时,两分钟内完成初始化的百分比分别是94.5%、96.4%、96.4%、90.9%、80%,三维定位误差RMS分别是2.67、1.62、1.49、1.48和1.47 cm,电离层约束标准差适中时可同时兼顾初始速度和定位精度。
| [1] |
ZUMBERGE J F, HEFLIN M B, JEFFERSON D C, et al. Precise point positioning for the efficient and robust analysis of GPS data from large networks[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B3): 5005-5017. DOI:10.1029/96JB03860 |
| [2] |
叶世榕. GPS非差相位精密单点定位理论与实现[D]. 武汉: 武汉大学, 2002. YE Shirong. Theory and implementation of GPS non-differential phase precision single point positioning[D]. Wuhan: Wuhan University, 2002. |
| [3] |
郭斐. GPS精密单点定位质量控制与分析的相关理论和方法研究[M]. 武汉: 武汉大学出版社, 2016. GUO Fei. Theory and methodology of quality control and quality analysis for GPS precise point positioning[M]. Wuhan: Wuhan University Press, 2016. |
| [4] |
李星星. GNSS精密单点定位及非差模糊度快速确定方法研究[D]. 武汉: 武汉大学, 2013. LI Xingxing. Rapid ambiguity resolution in GNSS precise point positioning[D]. Wuhan: Wuhan University, 2013. |
| [5] |
张小红, 李星星, 李盼. GNSS精密单点定位技术及应用进展[J]. 测绘学报, 2017, 46(10): 1399-1407. ZHANG Xiaohong, LI Xingxing, LI Pan. Review of GNSS PPP and its application[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1399-1407. DOI:10.11947/j.AGCS.2017.20170327 |
| [6] |
GENG Jianghui, SHI Chuang, GE Maorong, et al. Improving the estimation of fractional-cycle biases for ambiguity resolution in precise point positioning[J]. Journal of Geodesy, 2012, 86(8): 579-589. DOI:10.1007/s00190-011-0537-0 |
| [7] |
李盼. GNSS精密单点定位模糊度快速固定技术和方法研究[D]. 武汉: 武汉大学, 2016. LI Pan. Research on methodology of rapid ambiguity resolution for GNSS precise point positioning[D]. Wuhan: Wuhan University, 2016. |
| [8] |
LI Xingxing, LI Xin, YUAN Yongqiang, et al. Multi-GNSS phase delay estimation and PPP ambiguity resolution: GPS, BDS, GLONASS, Galileo[J]. Journal of Geodesy, 2018, 92(6): 579-608. DOI:10.1007/s00190-017-1081-3 |
| [9] |
GENG Jianghui, GUO Jiang, MENG Xiaolin, et al. Speeding up PPP ambiguity resolution using triple-frequency GPS/BeiDou/Galileo/QZSS data[J]. Journal of Geodesy, 2020, 94(1): 6. DOI:10.1007/s00190-019-01330-1 |
| [10] |
GE M, GENDT G, ROTHACHER M, et al. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations[J]. Journal of Geodesy, 2008, 82(7): 389-399. DOI:10.1007/s00190-007-0187-4 |
| [11] |
LAURICHESSE D, MERCIER F, BERTHIAS J P, et al. Integer ambiguity resolution on undifferenced GPS phase measurements and its application to PPP and satellite precise orbit determination[J]. Navigation, 2009, 56(2): 135-149. DOI:10.1002/j.2161-4296.2009.tb01750.x |
| [12] |
张宝成. GNSS非差非组合精密单点定位的理论方法与应用研究[J]. 测绘学报, 2014, 43(10): 1099. ZHANG Baocheng. Study on the theoretical methodology and applications of precise point positioning using undifferenced and uncombined GNSS data[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(10): 1099. |
| [13] |
WANG Zhiyu, LI Zishen, WANG Liang, et al. Assessment of multiple GNSS real-time SSR products from different analysis centers[J]. ISPRS International Journal of Geo-Information, 2018, 7(3): 85. DOI:10.3390/ijgi7030085 |
| [14] |
LI Yihe, GAO Yang, SHI Junbo. Improved PPP ambiguity resolution by COES FCB estimation[J]. Journal of Geodesy, 2016, 90(5): 437-450. DOI:10.1007/s00190-016-0885-x |
| [15] |
LIU Yanyan, YE Shirong, SONG Weiwei, et al. Estimating the orbit error of BeiDou GEO satellites to improve the performance of multi-GNSS PPP ambiguity resolution[J]. GPS Solutions, 2018, 22(3): 84. DOI:10.1007/s10291-018-0751-9 |
| [16] |
SHU Bao, LIU Hui, WANG Li, et al. Performance improvement of real-time PPP ambiguity resolution using a regional integer clock[J]. Advances in Space Research, 2021, 67(5): 1623-1637. DOI:10.1016/j.asr.2020.12.012 |
| [17] |
GENG J, TEFERLE F N, MENG X, et al. Towards PPP-RTK: ambiguity resolution in real-time precise point positioning[J]. Advances in Space Research, 2011, 47(10): 1664-1673. DOI:10.1016/j.asr.2010.03.030 |
| [18] |
WUBBENA G, SCHMITZ M, BAGGE A. PPP-RTK: precise point positioning using state-space representation in RTK networks[C]//Proceedings of the 18th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2005). Long Beach, CA, USA: [s. n. ], 2005: 2584-2594.
|
| [19] |
LI Xingxing, ZHANG Xiaohong, GE Maorong. Regional reference network augmented precise point positioning for instantaneous ambiguity resolution[J]. Journal of Geodesy, 2011, 85(3): 151-158. DOI:10.1007/s00190-010-0424-0 |
| [20] |
GE Maorong, DOUSA J, LI Xingxing, et al. A novel real-time precise positioning service system: global precise point positioning with regional augmentation[J]. Journal of Global Positioning Systems, 2012, 11(1): 2-10. DOI:10.5081/jgps.11.1.2 |
| [21] |
ZHANG Baocheng, TEUNISSEN P J G, ODIJK D. A novel un-differenced PPP-RTK concept[J]. The Journal of Navigation, 2011, 64(S1): S180-S191. DOI:10.1017/S0373463311000361 |
| [22] |
ZHNAG Baocheng, HOU Pengyu, ZHA Jiuping, et al. Integer-estimable FDMA model as an enabler of GLONASS PPP-RTK[J]. Journal of Geodesy, 2021, 95(8): 91. DOI:10.1007/s00190-021-01546-0 |
| [23] |
张宝成, ODIJK D. 一种能实现单频PPP-RTK的GNSS局域参考网数据处理算法[J]. 地球物理学报, 2015, 58(7): 2306-2319. ZHANG Baocheng, ODIJK D. A method for processing GNSS data from regional reference networks to enable single-frequency PPP-RTK[J]. Chinese Journal of Geophysics, 2015, 58(7): 2306-2319. |
| [24] |
MELBOURNE W G. The case for ranging in GPS based geodetic systems[C]//Proceedings of the 1st International Symposium on Precise Positioning with GPS. Rockville, MD, USA: U.S. Department of Commerce, 1985: 373-386.
|
| [25] |
WUBBENA G. Software developments for geodetic positioning with GPS using TI 4100 code and carrier measurements[C]//Proceedings of the 1st International Symposium on Precise Positioning with the Global Positioning System. Rockville, MD, USA: U.S. Department of Commerce, 1985: 403-412.
|
| [26] |
SCHMID R, STEIGENBERGER P, GENDT G, et al. Generation of a consistent absolute phase-center correction model for GPS receiver and satellite antennas[J]. Journal of Geodesy, 2007, 81(12): 781-798. DOI:10.1007/s00190-007-0148-y |
| [27] |
WU J, WU S, HAJJ G, et al. Effects of antenna orientation on GPS carrier phase[C]//Proceedings of the AAS/AIAA Astrodynamics Conference. San Diego, CA, USA: [s. n. ], 1992: 1647-1660.
|
| [28] |
LI Pan, ZHANG Xiaohong, REN Xiaodong, et al. Generating GPS satellite fractional cycle bias for ambiguity-fixed precise point positioning[J]. GPS Solutions, 2016, 20(4): 771-782. DOI:10.1007/s10291-015-0483-z |
| [29] |
LI Xingxing, ZHANG Xiaohong. Improving the estimation of uncalibrated fractional phase offsets for PPP ambiguity resolution[J]. The Journal of Navigation, 2012, 65(3): 513-529. DOI:10.1017/S0373463312000112 |
| [30] |
GU Shengfeng, LOU Yidong, SHI Chuang, et al. BeiDou phase bias estimation and its application in precise point positioning with triple-frequency observable[J]. Journal of Geodesy, 2015, 89(10): 979-992. DOI:10.1007/s00190-015-0827-z |
| [31] |
GENG Jianghui, MENG Xiaolin, DODSON A H, et al. Integer ambiguity resolution in precise point positioning: method comparison[J]. Journal of Geodesy, 2010, 84(9): 569-581. DOI:10.1007/s00190-010-0399-x |
| [32] |
SHI Junbo, GAO Yang. A comparison of three PPP integer ambiguity resolution methods[J]. GPS Solutions, 2014, 18(4): 519-528. DOI:10.1007/s10291-013-0348-2 |
| [33] |
郑艳丽. GPS非差精密单点定位模糊度固定理论与方法研究[D]. 武汉: 武汉大学, 2013. ZHENG Yanli. Research on integer ambiguity resolution in GPS precise point positioning[D]. Wuhan: Wuhan University, 2013. |
| [34] |
LOU Yidong, ZHANG Weixing, WANG C, et al. The impact of orbital errors on the estimation of satellite clock errors and PPP[J]. Advances in Space Research, 2014, 54(8): 1571-1580. DOI:10.1016/j.asr.2014.06.012 |
| [35] |
DAI L, WANG J, RIZOS C, et al. Predicting atmospheric biases for real-time ambiguity resolution in GPS/GLONASS reference station networks[J]. Journal of Geodesy, 2003, 76(11-12): 617-628. DOI:10.1007/s00190-002-0286-1 |
| [36] |
石鑫, 吕志伟, 孙航, 等. 网络RTK对流层改正数高程方向偏差修正[J]. 大地测量与地球动力学, 2016, 36(9): 817-820. SHI Xin, LV Zhiwei, SUN Hang, et al. The modification of tropospheric correction bias in vertical direction in network RTK[J]. Journal of Geodesy and Geodynamics, 2016, 36(9): 817-820. |
| [37] |
徐龙威. GNSS多模多频实时大规模网络RTK高精度定位关键技术研究[D]. 武汉: 武汉大学, 2018. XU Longwei. Research on the key technologies of GNSS multi-mode multi-frequency real-time large-scale network RTK high precision positioning[D]. Wuhan: Wuhan University, 2018. |
| [38] |
鄢子平, 丁乐乐, 黄恩兴, 等. 网络RTK参考站间模糊度固定新方法[J]. 武汉大学学报(信息科学版), 2013, 38(3): 295-298, 323. YAN Ziping, DING Lele, HUANG Enxing, et al. A new method of ambiguity resolution in network RTK between reference stations[J]. Geomatics and Information Science of Wuhan University, 2013, 38(3): 295-298, 323. |
| [39] |
LI Jinlong, YANG Yuanxi, XU Junyi, et al. GNSS multi-carrier fast partial ambiguity resolution strategy tested with real BDS/GPS dual- and triple-frequency observations[J]. GPS Solutions, 2015, 19(1): 5-13. DOI:10.1007/s10291-013-0360-6 |
| [40] |
VERHAGEN S, TEUNISSEN P J G. The ratio test for future GNSS ambiguity resolution[J]. GPS Solutions, 2013, 17(4): 535-548. DOI:10.1007/s10291-012-0299-z |
| [41] |
DAI Liwen, ESLINGER D, SHARPE T. Innovative algorithms to improve long range RTK reliability and availability[C]//Proceedings of 2007 National Technical Meeting of the Institute of Navigation. San Diego, CA, USA: [s. n. ], 2007: 860-872.
|
| [42] |
张绍成. 基于GPS/GLONASS集成的CORS网络大气建模与RTK算法实现[D]. 武汉: 武汉大学, 2010. ZHANG Shaocheng. The GPS/GLONASS integrated CORS network atmosphere modeling and RTK algorithm implementation[D]. Wuhan: Wuhan University, 2010. |



