2. 中国矿业大学环境与测绘学院, 江苏 徐州 221116
2. School of Environmental Science and Spatial Informatics, China University of Mining and Technology, Xuzhou 221116, China
有效波高(significant wave height,SWH)作为海洋动力环境监测的重要因素,对于远洋航运发展和海洋资源开发都非常重要。传统获取有效波高的方法常采用浮标,浮标以长期、自动、定点、定时、全天候的方式收集有关海洋环境各个要素的信息,但覆盖范围较小,成本较高,容易受到海面因素的影响。另一种获取有效波高的方法是采用卫星高度计[1-4],卫星高度计可提供全球覆盖范围和气候尺度的SWH数据,但是,现有的卫星高度计SWH产品的空间分辨率有限,限制了其科学应用价值。随着星载SAR卫星的不断发射,星载SAR为海浪研究和预报提供了有力的支持[5-7]。但其成本较为昂贵。
近年来,随着GNSS的迅速发展,GNSS技术不仅能够为用户提供导航定位和准确授时信息,还能提供全天时、全天候、不间断的L波段微波信号源。全球导航卫星系统反射测量(global navigation satellite system reflectometry,GNSS-R)被应用于海洋和陆地遥感领域(如海面风速反演[8]、海面高度反演[9]、雪深反演[10]、海冰探测[11]和土壤湿度反演[12]等),以其重访周期短、观测成本低等优点展现出巨大的潜力。文献[13]提出利用GNSS反射信号进行海洋测高。文献[14]首次进行岸基试验,提出利用GNSS反射信号与直达信号的干涉复数场(interferometric complex field, ICF)的有效相关时间函数反演海浪有效波高的方法,利用半经验模型将GNSS-R ICF相干时间与SWH联系起来,初步探讨了GNSS-R在近岸海域海况监测中的应用潜力。文献[15]建立了有效波高与合成孔径雷达回波信号信噪比平方根之间的线性关系。文献[16]也基于该关系模型,首次利用星载CYGNSS GNSS-R数据估算了全球海洋有效波高。文献[17]利用GNSS-R干涉图技术(interference pattern technique,IPT)反演SWH和平均海平面(mean sea surface level,MSSL),岸基试验结果表明,该方法估计的SWH和MSSL精度分别达6和4 cm。文献[18]利用L、S和Ku波段机会信号进行双基地雷达有效波高测量,将ICF相干时间方法用于3种波段的有效波高反演,并证实了该方法适用于在S波段、L波段和Ku波段3个频率上记录的数据。
针对岸基、船载和机载试验,国内学者也做了相关研究。文献[19]利用GNSS-R实测及超声波浪仪同步观测数据,计算了有效波高参数,与波浪仪实测数据对比,反演平均误差为2.88 cm。文献[20]讨论了干涉复数场及其相关时间,用三次多项式插值法估计相关时间,得到了新的海浪波高反演经验公式,将反演结果与声学波浪仪观测数据进行比对,结果表明两者比较一致。文献[21]通过对反射信号功率特征及信噪比的研究,提出了利用反射信号信噪比反演有效波高的方法。文献[22]建立了海面相关时间与波浪的有效波高和平均波周期的映射模型,试验结果表明,有效波高反演结果的均方误差为0.1 m。文献[23]进行了国内首次船载GNSS-R有效波高测量试验,通过与船上安装的WAVEX雷达波浪仪数据进行对比,二者之间的一致性验证了船载观测平台的可行性,为深入广泛开展GNSS-R海洋动力环境监测提供了依据。文献[24]在天津渤海湾特定区域进行了3次机载校飞试验,获得了大量有效GNSS-R信号数据,在DDM图谱基础上进行相关功率波形的计算,进而通过计算DCF(derivative of the correlation function)的函数波形宽度得到海面有效波高,验证了该方法的可行性。最近,英国、美国和中国已经分别成功发射了TechDemoSat-1(TDS-1)卫星[25]、CYGNSS[26]和BuFeng-1 A/B卫星[27],尽管GNSS-R技术为估计SWH提供了新的机会,然而针对基于星载GNSS-R技术的有效波高估计的研究非常有限。
综上所述,针对GNSS-R海浪有效波高反演研究,国内做了大量研究,但主要集中在岸基、船载和机载试验,针对星载平台的GNSS-R有效波高反演研究国内目前未有文献报道。
因此,本文利用基于CYGNSS卫星观测的GNSS-R延迟多普勒图(delay-Doppler maps,DDMs)获得的观测值研究GNSS-R在有效波高反演方面的潜力。首先,对DDM数据进行去噪和过滤处理以便对DDM数据进行质量控制。然后,从CYGNSS DDM数据中计算了4个观测值,并基于这4个观测值提出了一个有效波高反演经验模型,最后,对有效波高反演模型性能进行验证。
1 数据及预处理 1.1 数据为了开发海浪有效波高反演模型和测试模型性能,本文引入了3个数据集:CYGNSS卫星观测的GNSS-R L1级数据、欧洲中期天气预报中心(European Center for Medium-Range Weather Forecasts,ECMWF)再分析SWH数据和AVISO卫星高度计SWH数据。
1.1.1 CYGNSS GNSS-R数据CYGNSS由8颗小卫星组成,每颗CYGNSS卫星上都配备了4个延迟多普勒图测量仪(delay Doppler mapping instrument,DDMI),CYGNSS的原始DDM大小是128×20,其中128是时间延迟,20是多普勒频移。为了压缩传输的数据,将大小转换为17×11。目前,美国国家航空航天局(National Aeronautics and Space Administration,NASA)主要向用户免费开放3种级别的CYGNSS GNSS-R数据。本文下载的数据格式为NetCDF格式,采用的是L1级数据产品,数据版本为V 3.0,该类型数据分别记录了8颗CYGNSS卫星(CY01、CY02、CY03、CY04、CY05、CY06、CY07和CY08)的DDM、反射点坐标、发射机位置等相关信息。此外,CYGNSS L1 V3.0中还提供了多个DDM产品(如brcs、raw_counts、power_digital、power_analog)。本文使用power_analog产品,有关CYGNSS L1 V3.0数据的更多变量说明,请参阅CYGNSS L1 V3.0用户指南和数据字典(https://podaac-tools.jpl.nasa.gov/drive/files/allData/cygnss/L1/docs/148-0346-8_L1_v3.0_netCDF_Data_Dictionary.xlsx)。目前,该版本主要包含从2018年8月1日(DOY 213)—2022年8月6日的GNSS-R数据,可以从网站(https://podaac-tools.jpl.nasa.gov/drive/files/allData/cygnss/L3/v3.0)下载获得。考虑到数据量较大,本文仅下载了2019年4月1日—2019年5月31日CY01卫星观测的GNSS-R数据进行研究,对应DOY 091—DOY 151。
1.1.2 ECMWF再分析SWH数据哥白尼气候变化服务(Copernicus climate change service,C3S)气候数据库向用户免费开放ECMWF再分析数据产品,目前最新产品为ERA5数据,本文采用ERA5 SWH数据。ERA5提供了多种SWH产品,包括风浪和涌浪组合的SWH、风浪SWH和涌浪SWH。此外,ECMWF ERA5数据通常还提供不同涌浪相关的SWH(即significant wave height of first swell partition,significant wave height of second swell partition和significant wave height of third swell partition)。本文使用的是风浪和涌浪组合的SWH数据,其空间分辨率为0.5°×0.5°,时间分辨率为1 h,该数据是本文研究中采用的建模数据和模型测试数据,可从网站上(https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-single-levels)下载获取。
1.1.3 AVISO卫星高度计SWH数据本文采用的另一种模型测试数据是AVISO卫星高度计SWH数据。AVISO提供了不同类型的数据集,包括:①海面高度数据,主要用于海、湖泊或冰等表面高度测量,是高度计中最基本和最知名的产品;②增值产品,专门用于特定用途的更高级别产品(L4+),如涡流、海洋变化或冰冻圈研究;③风和海浪数据(如风速模量和有效波高),专门用于海况研究;④平均海平面测高产品等。本文采用的AVISO SWH数据的空间分辨率为0.1°×0.1°,时间分辨率为24 h。该数据集可通过网站(https://www.aviso.altimetry.fr/en/home.html)免费下载。
1.2 DDM去噪和数据过滤任何对地观测的遥感卫星数据均需要进行严格的质量控制,质量控制主要包括数据去噪和数据过滤两个方面。数据去噪通常采用的方法是将每个DDM对应的功率值减去噪底[28],也称为噪底减法。其噪声计算公式为
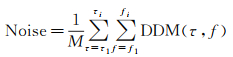 (1)
(1)
式中,τ1和τi为计算噪声区域选定的延迟码片的上下边界;f1和fi为计算噪声区域选定的频率的上下边界;M为选定噪声区域的像素数量。则去噪后的DDM计算公式可以表达为
 (2)
(2)
式中,DDMPower为未去噪的DDM功率值。
为了排除低质量的DDM测量数据,本文根据以下标准过滤数据[29]:
(1) 观测值需要具有良好的质量,这是由数据中的质量控制(quality control,QC)标志决定的。
(2) GNSS-R观测值及其对应的参考数据必须是正值。
(3) 当卫星跟踪器无法跟踪时所进行的测量将被丢弃。
(4) 选择距离陆地25 km以上的镜面反射点数据,以减少建模误差。
(5) 观测数据范围定义为纬度38°N—38°S和经度0°—360°。
(6) 镜面反射点方向上的接收天线增益(sp_rx_gain)大于0 dBi。
(7) 入射角范围为10°~40°。
1.3 GNSS-R观测值计算GNSS散射信号相关功率模型是从基尔霍夫(Kirchhoff Approximation,KA)近似的几何光学方法出发,在双基雷达方程的基础上提出的,可以写成曲面积分的形式[30]
 (3)
(3)
式中,〈y(τ, f)2〉为GNSS反射信号功率,是时间延迟τ和频率f的函数;Ti为相干积分时间;λ为信号波长;Pt和Gt为卫星发射功率和天线增益;Gr为接收机天线增益;Rt和Rr分别为卫星发射机到镜面反射点和镜面反射点到接收机的距离;Λ和S分别为伪码自相关函数和SINC函数;A为散射面积;σ0为双基地雷达散射截面(normalized bistatic radar cross section,NBRCS)[31]。
在之前的研究中,针对不同的GNSS-R应用已经提出了与DDM相关的几种观测值(如信噪比(SNR)、DDM能量均值(delay-Doppler map average,DDMA)、前沿斜率(leading edge slope,LES)和后沿斜率(trailing edge slope,TES)等),并且这些观测值已经在海面风速反演、海冰监测、土壤湿度反演等领域得到广泛讨论[25, 28, 32-33]。文献[16]将SNR观测值用于SWH估计,这项研究首次利用星载CYGNSS GNSS-R数据的SNR观测值来估计SWH,然而本文的研究与文献[16]在反演方法上有所不同。本文引入了归一化积分时延波形(normalized integral delay waveform,NIDW)用于计算4个GNSS-R观测值(即归一化积分时延波形前沿斜率(LES-NIDW)、归一化积分时延波形后沿斜率(TES-NIDW)、归一化积分时延波形前沿波形值之和(LEWS-NIDW)和归一化积分时延波形后沿波形值之和(TEWS-NIDW))[30, 34],并基于这4个观测值来进行星载GNSS-R SWH反演。它们的计算公式分别定义如下
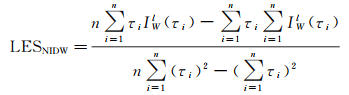 (4)
(4)
 (5)
(5)
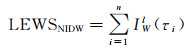 (6)
(6)
 (7)
(7)
式中,LESNIDW表示归一化积分时延波形的前沿斜率;TESNIDW表示归一化积分时延波形的后沿斜率;LEWSNIDW表示归一化积分时延波形的前沿波形值之和;TEWSNIDW表示归一化积分时延波形的后沿波形值之和;n表示参与计算的时延点数,在本文中,n=2;τi为延迟值,1个延迟等于0.25个码片(0.25 chips);IWl和IWt分别为积分时延波形前沿和后沿部分波形值;NIDW表示归一化积分时延波形,在计算归一化积分时延波形以前,需要先计算积分时延波形,其计算公式为
 (8)
(8)
式中,N是选定的多普勒频率数目(N=5);〈|y′(τ, fk)2|〉表示经去噪后选定的时延和多普勒频移范围内的反射信号功率值。
当对积分时延波形进行归一化处理后,可以得到归一化积分时延波形
 (9)
(9)
式中,IDWmax表示积分时延波形中的最大值。
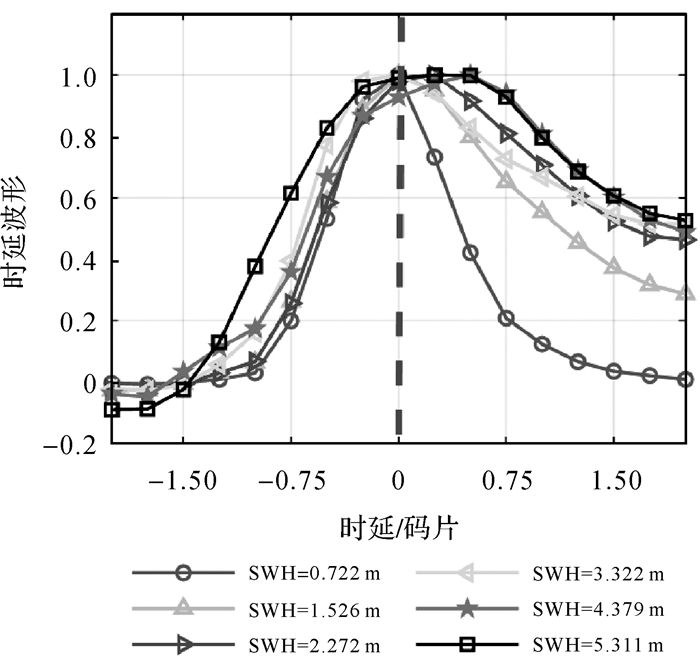
图 1和图 2分别给出了不同SNR值(对应不同的SWH值)情况下的DDM和不同有效波高的归一化积分时延波形。使用的数据是2019年4月30日海洋上收集的CYGNSS数据。为了便于说明和计算,不同有效波高的归一化积分时延波形均以时间延迟零值处作为前沿和后沿的分界点,并将其分割为前沿(leading edge,LE)和后沿(trailing edge,TE)两个部分(如图 2中虚线所示)。如图 1和图 2所示,不同有效波高的DDM图像不同,DDM之间的差异主要集中在“马蹄形”区域;另一方面,归一化积分时延波形的前沿和后沿部分的不同有效波高可以很容易地区别出来;此外,不同海浪有效波高下反射信号的时延波形曲线具有不同的特征,这些不同特征为利用GNSS-R信号反演海浪有效波高提供了新的机会。

|
| 图 1 不同SNR的DDM Fig. 1 DDM with different SNR |
|
| 图 2 不同SWH的归一化积分时延波形 Fig. 2 Normalized integral delay waveform (NIDW) with different SWH |
2 星载GNSS-R有效波高反演模型构建 2.1 建模方法
为了验证所提出方法的适用性和可靠性,本文下载并收集了1.1节描述的3种数据集,这些数据仅包含海洋上的数据,陆地上的数据不在本文研究范围之内。采用如1.2小节描述的方法对DDM数据进行质量控制后,从DDM中计算了4个有用的GNSS-R观测值,并利用DDM的数据采集时间和镜面反射点位置,通过空间上的双线性插值和时间上的线性插值,分别将ERA5 SWH产品、AVISO SWH产品数据分别与CYGNSS镜面点位置进行匹配,并通过随机选择将数据进一步划分为训练数据集和测试数据集,30%的数据样本用作训练集,其余70%的数据样本用作测试集。之后,将4个GNSS-R观测值和SWH分别作为输入和输出变量,采用最小二乘拟合建立海浪SWH反演模型。考虑到ERA5 SWH产品相比AVISO SWH产品数据具有更高的时空分辨率,因此,在开发海浪SWH反演模型时,本文仅采用ERA5 SWH数据进行训练模型。然后,将测试数据的GNSS-R观测值输入所得到的模型中,从而可以获得基于GNSS-R方法获得的SWH估计值。最后,为了进一步验证本文所提模型反演SWH的性能,将GNSS-R数据的SWH反演结果分别与ERA5 SWH产品和AVISO SWH产品数据进行比较,以评估本文所提方法的可行性。SWH反演模型的构建和测试流程算法如图 3所示。第1阶段是DDM处理和计算归一化积分时延波形,第2阶段是4个GNSS-R观测值提取,第3阶段是数据匹配,第4阶段是模型构建过程,第5阶段是模型性能评估。

|
| 图 3 星载GNSS-R方法SWH反演算法流程 Fig. 3 Flowchart of SWH retrieval algorithm of spaceborne GNSS-R method |
2.2 反演模型构建
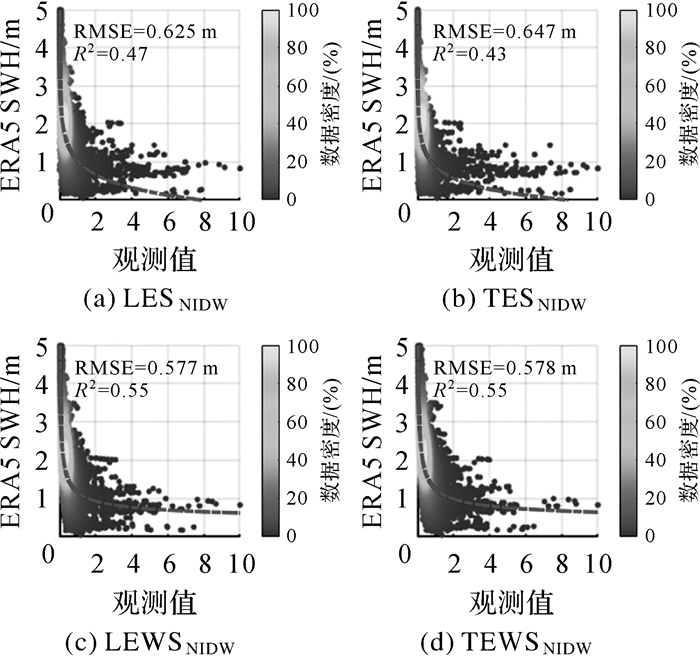
图 2展示了不同有效波高下的归一化积分时延波形。由图 2可以看出,归一化积分时延波形随有效波高的变化而变化,有效波高的变化越大,时延波形的变化越大。根据大量数据的曲线拟合试验,4个GNSS-R观测值与ERA5 SWH数据之间的关系可以用式(10)表示,基于4个观测值(即归一化积分时延波形前沿斜率,归一化积分时延波形后沿斜率,归一化积分时延波形前沿波形值之和,以及归一化积分时延波形后沿波形值之和)构建的有效波高模型如图 4中的虚线所示
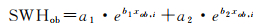 (10)
(10)
|
| 图 4 采用4个观测值构建的SWH反演模型 Fig. 4 SWH retrieval models constructed with 4 observables |
式中,xob分别表示4个观测值;其他符号是模型的拟合参数。
图 4给出了采用4个观测值数据构建的拟合模型曲线。图中散点分别代表 4个观测值与ERA5 SWH数据的关系,颜色栏表示数据密度,模型拟合的均方根误差(RMSE)和决定系数(R2)也在图中显示。由图 4可以看出,4个观测值的拟合模型曲线与散点拟合良好。其中,基于归一化积分时延波形前沿波形值之和与归一化积分时延波形后沿波形值之和构建的拟合模型的拟合性能在均方根误差和决定系数方面优于归一化积分时延波形前沿斜率和归一化积分时延波形后沿斜率。总体而言,基于4个观测值构建的拟合模型的决定系数大于0.43,相对偏低,主要原因是:4个观测值构建的拟合模型在低SWH值下的拟合性能较差。此外,由于训练数据集中缺少高SWH样本,因此很难获得理想的模型拟合性能。
3 模型验证 3.1 验证方法为了验证海浪SWH反演模型的性能,本小节将模型反演SWH分别与ERA5 SWH和AVISO SWH数据进行比较。此外,还将GNSS-R数据轨迹与ERA5 SWH数据分布进行比较,并分析了加勒比海及我国的黄海、东海和南海的SWH反演结果。采用均方根误差(root mean square error,RMSE)、平均绝对误差(mean absolute error,MAE)、皮尔逊相关系数(Pearson correlation coefficient, CC)和平均绝对百分比误差(mean absolute percentage error,MAPE)4个指标对模型反演SWH的性能进行评价。4个指标的计算公式如下
 (11)
(11)
 (12)
(12)
 (13)
(13)
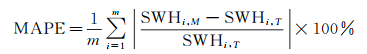 (14)
(14)
式中,m为数据样本数;SWHi, M和SWHi, T分别为模型估计SWH和从ERA5及AVISO再分析数据中获得的SWH;SWHM和SWHT分别为i, MSWH和i, TSWH的平均值。
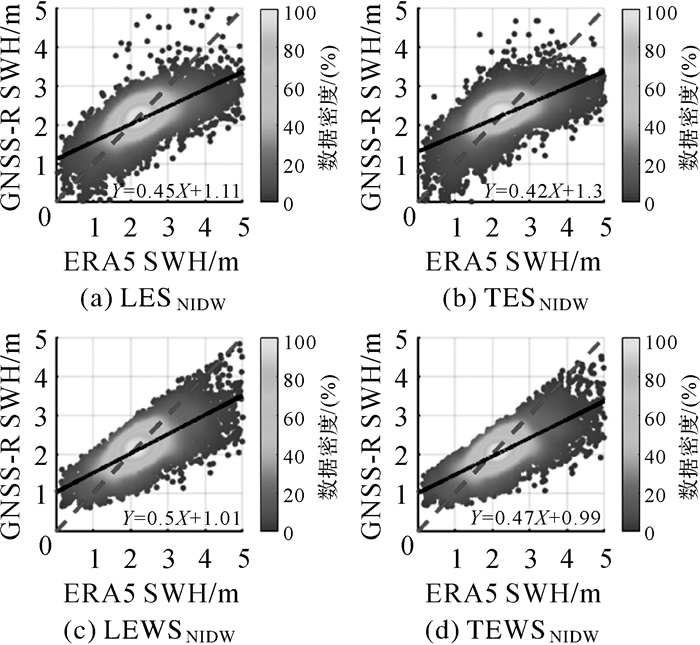
3.2 SWH反演模型可靠性验证 3.2.1 利用ERA5 SWH数据验证利用ERA5 SWH数据对4个GNSS-R观测值构建的SWH模型反演结果进行验证,如图 5所示。图 5给出了ERA5 SWH数据与4个观测值构建的反演模型估计的SWH的散点图,图中虚线为1∶1参考线,实线为4个观测值构建的SWH反演模型估计SWH与ERA5 SWH数据的线性拟合直线(Y=aX+b),表 1给出了模型反演性能的4个评价指标。由图 5可以看出,本文提出的基于归一化积分时延波形的4个观测值构建的SWH反演模型估计的SWH与ERA5 SWH数据在相关性方面表现良好。由表 1也可以看出,4个观测值构建的反演模型的反演结果的相关系数均大于0.65。此外,归一化积分时延波形前沿波形值之和与归一化积分时延波形后沿波形值之和两个观测值的反演性能在4个指标方面均优于归一化积分时延波形前沿斜率和归一化积分时延波形后沿斜率两个观测值。然而,归一化积分时延波形前沿斜率和归一化积分时延波形后沿斜率两个观测值的反演性能差异不大。总的来说,4个观测值在均方根误差和相关系数方面分别优于0.66 m和0.65。
|
| 图 5 ERA5 SWH数据与4个观测值构建的反演模型估计的SWH的散点 Fig. 5 Scatter plots of ERA5 SWH data and SWH estimated by retrieval model constructed based on 4 observables |
| 观测值 | RMSE/m | MAE/m | CC | MAPE/(%) |
| LESNIDW | 0.653 | 0.499 | 0.67 | 25.77 |
| TESNIDW | 0.656 | 0.508 | 0.65 | 27.35 |
| LEWSNIDW | 0.606 | 0.463 | 0.73 | 24.64 |
| TEWSNIDW | 0.633 | 0.478 | 0.73 | 24.54 |
3.2.2 利用AVISO SWH数据验证
本文将4个观测值构建的SWH反演模型的反演结果与AVISO SWH数据进行比较。图 6给出了AVISO SWH数据与4个观测值构建的SWH反演模型估计的SWH的散点图。图中虚线为1∶1参考线,实线为4个观测值构建的SWH反演模型估计SWH与AVISO SWH数据的线性拟合直线(Y=aX+b),表 2给出了模型反演结果与AVISO SWH数据对比的4个评价指标。由图 6和表 2可以看出,基于4个观测值构建的SWH反演模型的SWH估计结果与AVISO SWH数据均具有较好的相关性。除归一化积分时延波形后沿斜率观测值外,其他3个观测值反演SWH的结果与AVISO SWH数据的RMSE均小于0.66 m,并且相关系数大于0.72。通过以上两种参考数据的分析结果,进一步表明了本文所提的建模方法在星载GNSS-R SWH估计方面具有可行性和可靠性。

|
| 图 6 AVISO SWH数据与4个观测值构建的反演模型估计的SWH的散点 Fig. 6 Scatter plots of AVISO SWH data and SWH estimated by retrieval model constructed based on 4 observables |
| 观测值 | RMSE/m | MAE/m | CC | MAPE/(%) |
| LESNIDW | 0.649 | 0.527 | 0.73 | 24.97 |
| TESNIDW | 0.678 | 0.549 | 0.70 | 26.24 |
| LEWSNIDW | 0.659 | 0.538 | 0.72 | 25.34 |
| TEWSNIDW | 0.656 | 0.532 | 0.72 | 24.93 |
3.3 GNSS-R数据轨迹与ERA5 SWH数据分布比较
图 7为2019年5月基于CYGNSS数据的模型反演SWH结果与ERA5 SWH数据分布的比较。可以看出,基于4个GNSS-R观测值构建的模型反演结果与ERA5 SWH吻合较好。SWH的高值主要出现在高纬度地区,尤其是南纬地区。主要原因可能是由于全球气压的特定分布,导致高纬度地区风速较大。通常来说,SWH与海面风速呈正相关。由于CYGNSS轨道覆盖范围有限,目前无法使用CYGNSS数据估算北冰洋或南极洲周围海域的SWH。

|
| 图 7 2019年5月GNSS-R方法估计的SWH与ERA5 SWH数据全球分布的比较 Fig. 7 Comparison of SWH estimated by GNSS-R method with ERA5 SWH data global distribution May 2019 |
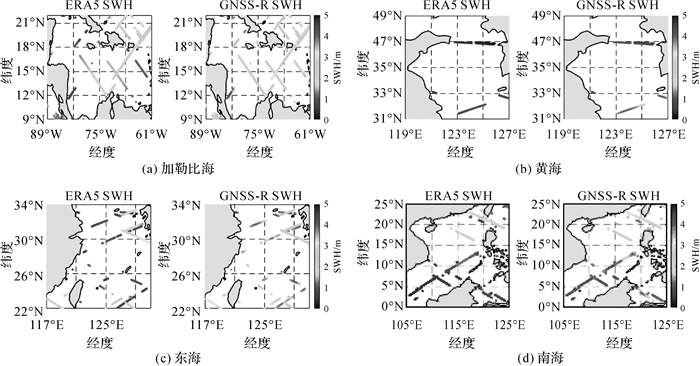
限于篇幅,图 8仅展示了2019年5月在加勒比海、黄海、东海和南海地区基于TEWS-NIDW观测值估计SWH与ERA5 SWH数据分布的比较结果。值得一提的是,由于CYGNSS卫星覆盖范围有限,目前无法采用GNSS-R方法获得我国整个渤海地区的SWH反演结果。由图 8可以看出,总体上,CYGNSS SWH与ERA5 SWH基本一致。然而,GNSS-R数据轨迹较为稀疏,这是因为在数据预处理步骤中排除了一些低质量的DDM数据,并且低质量的DDM通常会连续出现一段时间。此外,本文仅针对1颗CYGNSS卫星数据来构建模型和验证模型性能,这也是GNSS-R数据轨迹较为稀疏的是主要原因。未来,将同时采用8颗CYGNSS来进行SWH反演,相信GNSS-R数据轨迹将更为密集,将能实现更高空间分辨率和更高精度的SWH反演结果。
|
| 图 8 2019年5月在加勒比海、黄海、东海和南海地区基于TEWS-NIDW观测值估计SWH与ERA5 SWH数据分布的比较 Fig. 8 Comparison of SWH estimated by TEWS-NIDW observable with ERA5 SWH data distribution in the Caribbean Sea, Yellow Sea, East China Sea and South China Sea in May 2019 |
4 结论
本文采用从CYGNSS卫星观测的GNSS-R延迟多普勒图(DDM)中计算的4个观测值推导出海浪有效波高经验模型。为了进一步验证所提模型的可靠性、可行性和适用性,还分别将ERA5和AVISO SWH数据产品作为验证数据,并将反演模型的SWH估计结果与ERA5和AVISO SWH数据产品进行比较和分析。主要结论如下:
(1) 采用ERA5 SWH数据作为验证数据时,归一化积分时延波形的前沿和后沿波形值之和两个观测值在均方根误差、平均绝对误差、相关系数和平均绝对百分比误差方面,均优于归一化积分时延波形的前沿和后沿斜率两个观测值。然而,归一化积分时延波形前沿斜率和归一化积分时延波形后沿斜率两个观测值的反演性能差异不大。总体而言,4个观测值在均方根误差和相关系数方面分别优于0.66 m和0.65。
(2) 采用AVISO SWH数据作为验证数据时,基于4个观测值构建的SWH反演模型的SWH估计结果与AVISO SWH数据均具有较好的相关性(相关系数均大于0.7)。除归一化积分时延波形后沿斜率观测值外,其他3个观测值反演SWH的结果与AVISO SWH数据的RMSE均小于0.66 m,并且相关系数大于0.72。进一步表明了本文所提的建模方法在星载GNSS-R SWH估计方面具有可行性和可靠性。
(3) 从GNSS-R方法估计SWH与ERA5 SWH数据全球分布的比较结果来看,CYGNSS SWH与ERA5 SWH基本一致。然而,由于CYGNSS轨道覆盖范围有限,目前无法使用CYGNSS数据估算北冰洋或南极洲周围海域的SWH。
笔者今后将同时采用8颗CYGNSS来构建SWH反演模型,以实现更高空间分辨率和更高精度的SWH反演结果。此外,将深入了解卫星和其他因素(如GNSS-R接收机、天线增益、信号噪声、入射角和海面风速等)的影响来提高星载GNSS-R有效波高反演性能。
致谢: 特别感谢美国航空航天局(NASA)免费提供CYGNSS数据、欧洲中期天气预报中心(ECMWF)和AVISO数据中心免费提供SWH数据。
| [1] |
HAO Zengzhou, TU Qianguang, ZHANG Siqi, et al. Wind-wave relationship model and analysis of typhoon wave fields in the South China Sea from HY-2A satellite observations[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2020, 13: 4008-4015. DOI:10.1109/JSTARS.2020.3007495 |
| [2] |
JIA Yongjun, YANG Jungang, LIN Mingsen, et al. Global assessments of the HY-2B measurements and cross-calibrations with Jason-3[J]. Remote Sensing, 2020, 12(15): 2470. DOI:10.3390/rs12152470 |
| [3] |
WANG Jiuke, AOUF L, JIA Yongjun, et al. Validation and calibration of significant wave height and wind speed retrievals from HY2B altimeter based on deep learning[J]. Remote Sensing, 2020, 12(17): 2858. DOI:10.3390/rs12172858 |
| [4] |
JIA Yongjun, LIN Mingsen, ZHANG Youguang. Evaluations of the significant wave height products of HY-2B satellite radar altimeters[J]. Marine Geodesy, 2020, 43(4): 396-413. DOI:10.1080/01490419.2020.1750513 |
| [5] |
PRAMUDYA F S, PAN Jiayi, DEVLIN A T. Estimation of significant wave height of near-range traveling ocean waves using Sentinel-1 SAR images[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2019, 12(4): 1067-1075. DOI:10.1109/JSTARS.2019.2902566 |
| [6] |
SHAO W Z, HU Y Y, ZHENG G, et al. Sea state parameters retrieval from cross-polarization Gaofen-3 SAR data[J]. Advances in Space Research, 2020, 65(3): 1025-1034. DOI:10.1016/j.asr.2019.10.034 |
| [7] |
WAN Yong, ZHANG Rongjuan, PAN Xiaodong, et al. Evaluation of the significant wave height data quality for the Sentinel-3 synthetic aperture radar altimeter[J]. Remote Sensing, 2020, 12(18): 3107. DOI:10.3390/rs12183107 |
| [8] |
HAMMOND M L, FOTI G, GOMMENGINGER C, et al. Temporal variability of GNSS-reflectometry ocean wind speed retrieval performance during the UK TechDemoSat-1 mission[J]. Remote Sensing of Environment, 2020, 242: 111744. DOI:10.1016/j.rse.2020.111744 |
| [9] |
LI Weiqiang, RIUS A, FABRA F, et al. Revisiting the GNSS-R waveform statistics and its impact on altimetric retrievals[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(5): 2854-2871. DOI:10.1109/TGRS.2017.2785343 |
| [10] |
YU Kegen, LI Yunwei, CHANG Xin. Snow depth estimation based on combination of pseudorange and carrier phase of GNSS dual-frequency signals[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(3): 1817-1828. DOI:10.1109/TGRS.2018.2869284 |
| [11] |
YAN Qingyun, HUANG Weimin, MOLONEY C. Neural networks based sea ice detection and concentration retrieval from GNSS-R delay-Doppler maps[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(8): 3789-3798. DOI:10.1109/JSTARS.2017.2689009 |
| [12] |
CAMPS A, PARK H, CASTELLVÍ J, et al. Single-pass soil moisture retrievals using GNSS-R: lessons learned[J]. Remote Sensing, 2020, 12(12): 2064. DOI:10.3390/rs12122064 |
| [13] |
MARTIN-NEIRA M. A passive reflectometry and interferometry system (PARIS): application to ocean altimetry[J]. ESA Journal, 1993. |
| [14] |
SOULAT F, CAPARRINI M, GERMAIN O, et al. Sea state monitoring using coastal GNSS-R[J]. Geophysical Research Letters, 2004, 31(21): L21303. |
| [15] |
ALPERS W, HASSELMANN K. Spectral signal to clutter and thermal noise properties of ocean wave imaging synthetic aperture radars[J]. International Journal of Remote Sensing, 1982, 3(4): 423-446. DOI:10.1080/01431168208948413 |
| [16] |
PENG Qin, JIN Shuanggen. Significant wave height estimation from space-borne cyclone-GNSS reflectometry[J]. Remote Sensing, 2019, 11(5): 584. DOI:10.3390/rs11050584 |
| [17] |
ALONSO-ARROYO A, CAMPS A, PARK H, et al. Retrieval of significant wave height and mean sea surface level using the GNSS-R interference pattern technique: results from a three-month field campaign[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(6): 3198-3209. DOI:10.1109/TGRS.2014.2371540 |
| [18] |
SHAH R, GARRISON J L, EGIDO A, et al. Bistatic radar measurements of significant wave height using signals of opportunity in L-, S-, and Ku-bands[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(2): 826-841. DOI:10.1109/TGRS.2015.2466682 |
| [19] |
王鑫, 孙强, 张训械, 等. 中国首次岸基GNSS-R海洋遥感实验[J]. 科学通报, 2008(5): 589-592. WANG Xin, SUN Qiang, ZHANG Xunxie, et al. China's first shore based GNSS-R ocean remote sensing experiment[J]. Chinese Science Bulletin, 2008(5): 589-592. DOI:10.3321/j.issn:0023-074X.2008.05.015 |
| [20] |
邵连军, 张训械, 王鑫, 等. 利用GNSS-R信号反演海浪波高[J]. 武汉大学学报(信息科学版), 2008, 33(5): 475-478. SHAO Lianjun, ZHANG Xunxie, WANG Xin, et al. Sea surface wave height retrieve using GNSS-R signals[J]. Geomatics and Information Science of Wuhan University, 2008, 33(5): 475-478. |
| [21] |
金玲. GNSS-R接收机及有效波高反演方法研究[D]. 北京: 北京化工大学, 2016. JIN Ling. Research on receiver and inversion method of significant wave height based on GNSS-R[D]. Beijing: Beijing University of Chemical Technology, 2016. |
| [22] |
王波, 闫星魁, 徐宇柘, 等. 岸基GNSS反射信号的波浪多参数反演方法研究[J]. 电波科学学报, 2019, 34(3): 315-321. WANG Bo, YAN Xingkui, XU Yuzhe, et al. Retrieving method of multi ocean wave parameters based on GNSS-R technique[J]. Chinese Journal of Radio Science, 2019, 34(3): 315-321. DOI:10.13443/j.cjors.2018101201 |
| [23] |
李颖, 朱雪瑗, 崔璨, 等. 船载GNSS-R有效波高测量的初步研究[J]. 海洋环境科学, 2016, 35(2): 180-183. LI Ying, ZHU Xueyuan, CUI Can, et al. Preliminary study on ship-borne significant wave height measurement using GNSS-R signals[J]. Marine Environmental Science, 2016, 35(2): 180-183. |
| [24] |
徐飞, 孙协昌, 刘馨宁, 等. 利用机载GNSS-R的有效波高反演技术[J]. 飞行器测控学报, 2017, 36(3): 212-218. XU Fei, SUN Xiechang, LIU Xinning, et al. A method of retrieval of significant wave height using airborne GNSS-R[J]. Journal of Spacecraft TT & C Technology, 2017, 36(3): 212-218. |
| [25] |
FOTI G, GOMMENGINGER C, JALES P, et al. Spaceborne GNSS reflectometry for ocean winds: first results from the UK TechDemoSat-1 mission[J]. Geophysical Research Letters, 2015, 42(13): 5435-5441. DOI:10.1002/2015GL064204 |
| [26] |
CLARIZIA M P, RUF C S. Wind speed retrieval algorithm for the cyclone global navigation satellite system (CYGNSS) mission[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(8): 4419-4432. DOI:10.1109/TGRS.2016.2541343 |
| [27] |
JING Cheng, NIU Xinliang, DUAN Chongdi, et al. Sea surface wind speed retrieval from the first Chinese GNSS-R mission: technique and preliminary results[J]. Remote Sensing, 2019, 11(24): 3013. |
| [28] |
YAN Qingyun, HUANG Weimin. Spaceborne GNSS-R sea ice detection using delay-Doppler maps: first results from the U.K. TechDemoSat-1 mission[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(10): 4795-4801. |
| [29] |
CLARIZIA M P, RUF C S. Statistical derivation of wind speeds from CYGNSS data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(6): 3955-3964. |
| [30] |
ZAVOROTNY V U, VORONOVICH A G. Scattering of GPS signals from the ocean with wind remote sensing application[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(2): 951-964. |
| [31] |
HUANG Feixiong, GARRISON J L, LEIDNER S M, et al. A forward model for data assimilation of GNSS ocean reflectometry delay-Doppler maps[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(3): 2643-2656. |
| [32] |
BU Jinwei, YU Kegen, ZHU Yongchao, et al. Developing and testing models for sea surface wind speed estimation with GNSS-R delay Doppler maps and delay waveforms[J]. Remote Sensing, 2020, 12(22): 3760. |
| [33] |
DONG Zhounan, JIN Shuanggen. Evaluation of the land GNSS-reflected DDM coherence on soil moisture estimation from CYGNSS data[J]. Remote Sensing, 2021, 13(4): 570. |
| [34] |
ZHU Yongchao, TAO Tingye, YU Kegen, et al. Sensing Sea ice based on Doppler spread analysis of spaceborne GNSS-R data[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 13: 217-226.
|



