我国地质灾害每年都造成严重的人员伤亡和财产损失,其中滑坡灾害所占比重最大,约占全国地质灾害总发生数的60%以上[1-2]。如何对滑坡体进行高精度实时监测预警,了解和掌握灾害的变形规律和变形特征是实现滑坡灾害有效防治的前提[3]。随着全球导航卫星系统(GNSS)的快速发展,尤其是北斗三号卫星导航全球组网完成,GNSS技术定位性能的准确性、可靠性、时效性、易用性不断提高,已成为实时获取滑坡地表三维变形的主要技术手段[4-5]。
在GNSS滑坡监测中,最常用的是单基准站解算的动态相对定位技术(RTK),这种技术使用单个基准站为多个监测站提供数据,一旦基准站由于设备异常、电源不足等问题发生数据中断,会严重影响监测结果的连续性和可靠性[6-8]。针对这个问题,有两种解决方法:一种是利用精密单点定位技术(PPP)直接进行监测。文献[9]利用6个连续台站的GNSS观测数据分析北斗卫星导航系统(BDS)PPP技术的精度及其稳定性,证明BDS可以用于监测变形量较大的地壳运动。文献[10]通过波多黎各和维尔京群岛周围8个永久站的数据建立区域稳定参考框架,实现基于PPP技术的毫米级精准监测。但是这些PPP监测技术都是事后处理,并且出现中断或异常时需要较长时间的初始化,难以满足实时监测的需求。另一种是使用稳定的国际地球参考框架(ITRF)点或多个基准站进行网解。文献[11]以大面积矿区周围国际GNSS服务(IGS)跟踪站为基准站,建立高精度GNSS变形监测网,可以高效准确地监测大面积矿区沉降,但对于滑坡等小范围区域的变形监测,与IGS跟踪站之间距离较远,基准站的误差经过传递被放大,导致其定位结果不能满足滑坡监测的要求。文献[12]在大坝监测区域建立两个基准站,但这种额外的基准站不仅增加了成本,还增加数据处理的复杂性。
针对基于RTK技术的滑坡监测基准站数据中断的问题,本文提出基准站中断时切换监测站为新基准站的方法以保障监测结果的连续性。同时顾及新基准站的运动状态和不稳定性,对切换后产生的误差进行改正,在不增加额外成本的同时,保障监测的连续性和预警的及时性。通过实例研究,验证本文方法的可行性和正确性。
1 数学模型 1.1 位移的参考基准地表位移的长期持续监测对滑坡灾害的成功预警至关重要。为了精确地描述滑坡运动,需要确定合适的参考基准,并保证参考基准的一致性[13-14]。目前在GNSS变形监测中,常常采用两种参考基准,一种是全球框架基准,另一种是局部固定基准。
(1) 全球框架基准。全球框架基准是一种全球性的、连续自洽的、且不断精化的框架基准。全球框架基准利用稳定的ITRF参考框架点或IGS站作为基准点,并对基准点的坐标和GPS精密星历施加约束,使其强制符合到基准点坐标框架上[15]。采用全球框架基准进行变形分析,能够获得测区整体变形趋势,对于大范围的变形监测,如全球板块运动监测、大区域地表变形监测等,常常选取全球框架基准。
(2) 局部固定基准。局部固定基准在测区内选取相对稳定点作为基准点,其坐标在各期监测中固定不变,并将监测网强制附合到基准点上[16]。与全球框架基准相比,这种基准不用考虑大尺度下的构造运动,能较好地反映测区内各点之间的相对变形情况,对于监测区域较小的变形监测,如滑坡变形监测、大坝变形监测等,常选取局部固定基准。
滑坡变形区域通常较小,仅需获取各变形点的相对变形信息,无须求解在全球参考框架中的绝对位置,因此通常采用局部固定基准[17]。这种基准对基准站的稳定性要求较高,当基准站由于设备异常、电源不足等问题发生中断时,将对滑坡监测结果的连续性和可靠性产生严重影响,针对这一问题,本文提出切换监测站为新基准站的方法以保障监测结果的连续可靠。但是由于新基准站自身的不稳定性,获得的监测结果包含额外的基准误差,无法反映真实变形结果,需要对基准误差进行改正[18]。
1.2 顾及运动状态改正的新基准站位移计算在切换基准站的过程中,受新基准站位移的影响,新基准站实际坐标可能发生变化,本节分析新基准站的稳定性并建立位移模型以获取新基准站位移。新基准站前期获取的监测坐标转换到局部坐标系(E, N, U),坐标系原点为首次监测坐标,即可得到新基准站的位移-时间序列。基于该序列及滑坡体变形演化规律[19],将新基准站的运动状态划分为4个阶段:稳定未变形阶段、匀速变形阶段、变速变形阶段、混合变形阶段。
(1) 稳定未变形阶段。新基准站处于稳定性相对较好的斜坡上,其位移-时间序列未出现明显的变形,可以不进行平面和高程上的速率改正,其位移模型如下
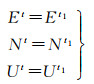 (1)
(1)
式中,t1、t分别代表基准站中断时刻和本次监测时刻。
(2) 匀速变形阶段。此阶段新基准站位移-时间序列总体趋势为一条倾斜直线,宏观变形速率基本保持不变,因此,需要对基准站分别在平面和高程上的速率进行改正,其位移模型如下
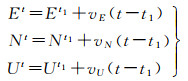 (2)
(2)
式中,vE、vN、vU分别代表平面和高程方向的运动速率。
(3) 变速变形阶段。在坡体变形初期或发展到一定阶段后,位移-时间序列的斜率表现出逐渐变化的趋势。可以根据这一变形阶段的监测数据,采用合适的预测模型进行拟合外推预测,其位移模型如下
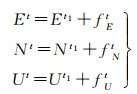 (3)
(3)
式中,ftE、ftN、ftU分别代表平面和高程方向的拟合外推改正的结果。
(4) 混合变形阶段。实际上,新基准站的运动状态可能改变导致上述方法失效,可借助PPP技术定期对新基准站进行检核,当检核不通过时,使用PPP定位结果建立位移模型。具体方法为将PPP定位结果转换到局部坐标系(EP, NP, UP)下,得到检核解的位移模型
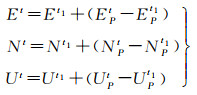 (4)
(4)
由于PPP技术监测结果的内符合精度可以达到10 mm[20],根据拉依达准则,设置检核阈值为30 mm。当连续3 d检核解与预测解的差值大于阈值时,排除PPP定位精度的影响,运动状态发生了改变,此时使用检核解的位移模型作为检核不通过的应急预案。
以上几种运动状态中,稳定未变形阶段与匀速变形阶段的改正方法简单准确且占演化过程中的时间最长,因此新基准站选取时应结合历史观测数据及实地监测环境,优先考虑这两种运动状态。
1.3 基准站不稳定对监测结果的影响局部固定基准的基准站坐标在各期监测中保持固定不变,与基准站实际坐标存在差异,本节分析基准站不稳定对监测结果的影响。假设分别有基准站i、监测站j对卫星p进行同步观测,分别列出线性化的载波相位观测方程如下
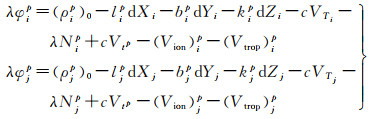 (5)
(5)
式中,λ为波长;φ为载波相位观测值;ρ0为测站近似位置与卫星之间的距离;l、b、k为线性化后的方向余弦;(dX、dY、dZ)为坐标改正数;c为光速;VT为接收机钟差;N为模糊度;Vt为卫星端钟差;Vion为电离层改正;Vtrop为对流层改正。
两式相减得
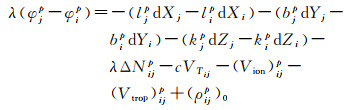 (6)
(6)
式中,ΔNijp=Njp-Nip;VTij=VTj-VTi;(Vion)ijp= (Vion)jp-(Vion)ip;(Vtrop)ijp=(Vtrop)jp-(Vtrop)ip;(ρijp)0=(ρjp)0-(ρip)0。
假设基准站i沿X轴方向位移m,即dXi中加上m,为保证等式(6)成立,基线向量的另一端需平移n
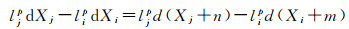 (7)
(7)
式中,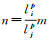
这就意味着,基准站发生位移时,基线向量也随之变化,其大小取决于m及基线向量的长短,基线向量越长,两端的方向余弦lip和ljp的差异就会越大。在常规的滑坡监测场景中,基线长度一般较短,lip和ljp的差异可以被忽略,基线向量另一端的移动量n与基准站位移量m相等,即
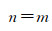 (8)
(8)
依据上述推导,基准站坐标保持不变的情况下解算得到的监测站位移存在大小为m的基准误差,方向与基准站位移方向相反。利用这一特点,在获取基准站位移模型后,可对各个监测站的监测结果进行改正,其改正模型如下
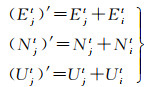 (9)
(9)
式中,(Ejt)′、(Njt)′、(Ujt)′分别代表改正后的监测结果。
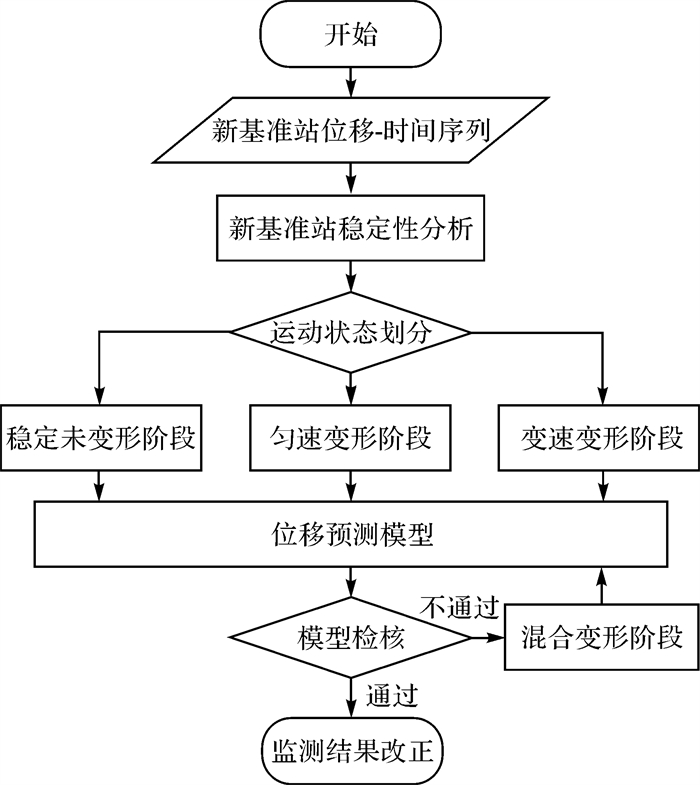
顾及运动状态改正的基准站切换实现过程见图 1。
|
| 图 1 顾及运动状态改正的基准站切换方法实现过程 Fig. 1 Flowchart of reference station switching method considering the correction of the motion state |
2 实例研究——甘肃黑方台滑坡监测基准站切换 2.1 黑方台滑坡概况
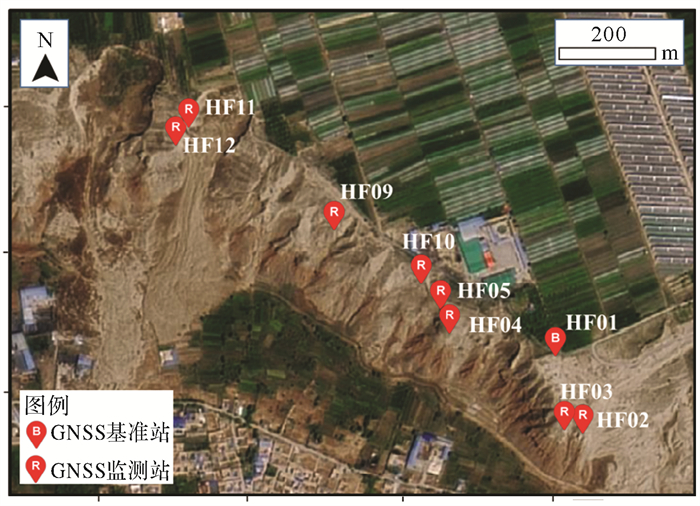
本文研究区域为黑方台党川滑坡,位于甘肃省临夏州永靖县盐锅峡镇黄河北岸,滑坡主体距离下方居民区水平距离约400 m,坡体正下方为水渠和农田[21]。为对黑方台滑坡的变形灾变演化进行准确的预警,2018年10月在台塬顶部布设9套多模多频低成本GNSS监测设备,具体监测点分布如图 2所示,其中HF01为基准站,布设在稳定区域,各监测站横向部设在台体边缘。数据处理软件采用长安大学北斗云实时监测软件平台[22-23],解算模式为GPS+BDS双系统组合定位,模糊度固定策略为部分固定,卫星截止高度10°,星历采用广播星历。
|
| 图 2 GNSS监测点位分布 Fig. 2 Distribution of GNSS monitoring points |
2020年2月1日由于HF01基准站数据发生中断,所有监测站无法获得可靠的监测结果。为了保障监测数据的连续采集和及时预警,综合考虑历史观测数据及实地监测环境,选取处于匀速变形阶段的HF02监测站为新基准站,固定不变坐标为首次监测的相对定位结果,此后所有监测站开始正常监测。2020年5月22日在HF01基准站修复好后切换回该站,2020年7月20日HF10监测站附近发生了一起滑坡,因此需要对新基准站进行稳定性分析并改正基准误差。
2.2 新基准站HF02稳定性分析首先对该站进行稳定性分析,根据监测软件处理得到的实时解,计算每日实时解的中位数为当日中位数解,得到的新基准站HF02的局部坐标系下的(E、N、U)位移-时间序列,如图 3所示。由图 3中实时解的结果可知,GNSS实时变形监测的实时解精度为厘米级,在3个方向上均满足实时监测需求,但仍然存在缺失数据、异常值和随机噪声,为数据分析带来困难,而中位数解有效避免了异常值和噪声对提取结果的影响,并使数据间隔固定为1 d,符合高精度时间序列分析的需要。

|
| 图 3 新基准站HF02的位移-时间序列结果 Fig. 3 Displacement time series results of HF02 new reference station |
由中位数解可知,监测时段内E、N、U 3个方向的相对位移分别为15.1、5.8、26.9 mm,宏观变形速率基本保持不变,新基准站的运动状态为匀速变形阶段。为了准确计算新基准站的运动状态改正参数,即中断时刻(2020年2月1日)的位移及速率改正,使用一次多项式对中位数解拟合得到E、N、U 3个方向的中断时刻位移分别为48.8、52.4、51.4 mm,速率改正为0.05、0.02、0.09 mm/d,根据式(2)获得新基准站的位移模型(如图 3计算解所示)。同时,采用PPP技术对新基准站进行定期检核,检核结果如图 3检核解所示,未超过检核阈值,可知新基准站运动状态未发生改变。
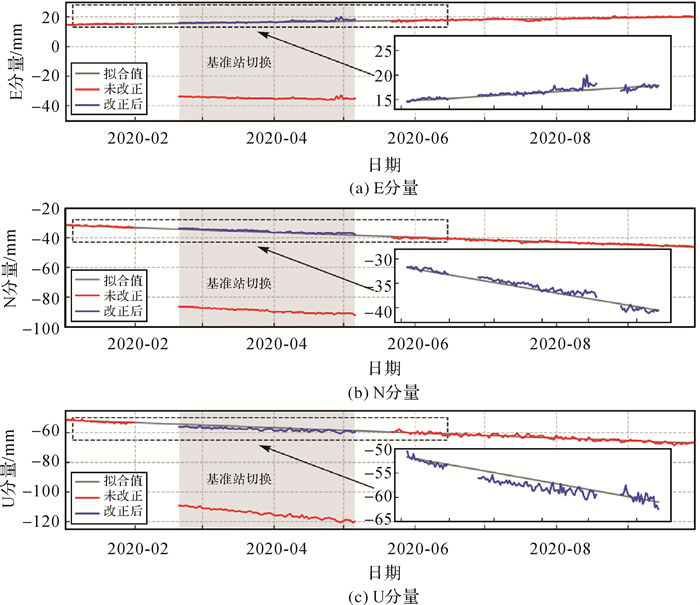
2.3 基准误差改正结果以距离HF01基准站直线距离884 m的监测站HF12监测数据为例分析改正效果。改正前该监测站的位移-时间序列如图 4所示,受基准站切换的影响存在基准误差,根据式(9)对其进行改正,部分统计结果见表 1。经过基准偏差的改正,3个方向上的位移-时间序列的连续性有明显的改善。
|
| 图 4 基准误差改正结果与拟合值比较 Fig. 4 Datum error correction results and compare with fitted value |
| 日期 | 未改正 | 拟合值 | 改正后 | ||||||||
| E | N | U | E | N | U | E | N | U | |||
| 2020-02-20 | -33.9 | -86.6 | -109.2 | 15.8 | -34.6 | -54.7 | 16.0 | -34.0 | -56.4 | ||
| 2020-02-26 | -34.4 | -86.7 | -110.0 | 15.9 | -34.9 | -55.1 | 15.9 | -34.0 | -56.6 | ||
| 2020-03-04 | -34.4 | -87.3 | -111.7 | 16.0 | -35.4 | -55.5 | 16.2 | -34.5 | -57.1 | ||
| 2020-03-11 | -34.4 | -87.9 | -111.7 | 16.1 | -35.8 | -55.9 | 16.4 | -35.0 | -56.9 | ||
| 2020-03-18 | -34.9 | -88.4 | -113.3 | 16.2 | -36.2 | -56.2 | 16.3 | -35.4 | -57.9 | ||
| 2020-03-25 | -35.2 | -88.7 | -114.2 | 16.3 | -36.6 | -56.6 | 16.3 | -35.6 | -58.0 | ||
| 2020-04-01 | -35.3 | -90.3 | -115.8 | 16.5 | -37.0 | -57.0 | 16.6 | -37.1 | -58.9 | ||
| 2020-04-08 | -35.1 | -89.7 | -114.8 | 16.6 | -37.4 | -57.3 | 17.1 | -36.3 | -57.3 | ||
| 2020-04-15 | -35.4 | -91.2 | -116.6 | 16.7 | -37.8 | -57.7 | 17.1 | -37.7 | -58.3 | ||
| 2020-04-22 | -35.6 | -91.4 | -118.8 | 16.8 | -38.2 | -58.0 | 17.2 | -37.8 | -59.9 | ||
| 2020-04-29 | -35.3 | -90.6 | -120.3 | 16.9 | -38.6 | -58.4 | 17.8 | -36.8 | -60.6 | ||
| 2020-05-06 | -35.2 | -92.2 | -120.0 | 17.0 | -38.9 | -58.7 | 18.3 | -38.3 | -59.6 | ||
| 平均变形速率/(mm/d) | -0.02 | -0.07 | -0.14 | 0.02 | -0.06 | -0.05 | 0.03 | -0.06 | -0.04 | ||
| MAE | - | - | - | - | - | - | 0.5 | 0.8 | 1.4 | ||
| RMSE | - | - | - | - | - | - | 0.7 | 0.9 | 1.5 | ||
该监测站序列3个方向仅位移1 cm左右且变形速率较小,处于匀速变形阶段,因此对序列进行线性拟合并视其为真实变形量,依此计算平均绝对误差(MAE)和均方根误差(RMSE)评价改正效果,评价结果见表 1。在对基准误差进行改正后,与真实变形较为一致,3个方向的MAE为0.5、0.8、1.4 mm,RMSE为0.7、0.9、1.5 mm,满足滑坡监测的需求。
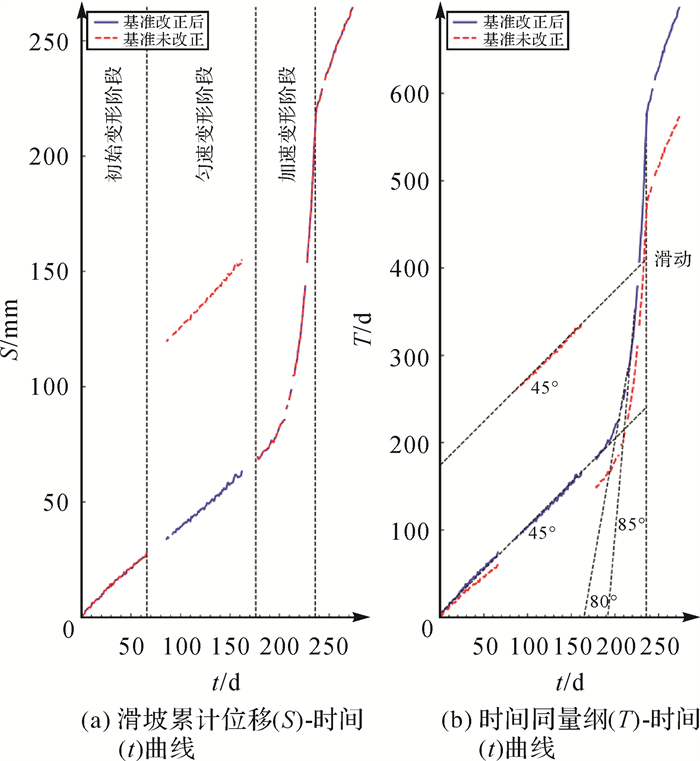
2.4 基准站切换对滑坡预警判据的影响2020年7月20日HF10附近发生了一起滑坡,其三维方向的累计位移-时间序列如图 5(a)所示,时间范围为2019年11月27日—2020年8月26日。本节以文献[24]提出的改进型切线角为预警判据评价基准站切换对滑坡预警的影响。相比于传统的切线角,使用累计位移除以匀速变形阶段变形速率保证了纵坐标与横坐标轴量纲一致。根据改进型切线角的计算方法,选取2020年2月20日—2020年5月6日为等速变形阶段,得到未改正时等速变形阶段三维方向平均变形速率为0.46 mm/d,改正后为0.38 mm/d。累计位移除以等速变形阶段平均变形速率,得到量纲统一的T-t曲线,如图 5(b)所示,可以看出基准误差改正前后统一量纲曲线会存在较大差异。
|
| 图 5 基准改正前后累计位移曲线 Fig. 5 Cumulative displacement graph before and after datum correction |
参考黑方台区域已有的成功预警案例,依据改进型切线角α确定滑坡变形阶段及预警等级[23, 25]。45° < α < 80°时,为初加速变形阶段,可发布黄色预警;80° < α < 85°时,为中加速变形阶段,可发布橙色预警;α>85°时,为加加速变形阶段,此时为红色预警。根据以上判据,改正后2020年6月24日改进型切线角超过80°,进入中加速变形阶段;7月7日,改进型切线角超过85°,进入加加速变形阶段。而未改正时2020年6月29日改进型切线角超过80°,与改正后相比延后了5 d;7月12日,改进型切线角超过85°,与改正后相比同样延后5 d。滑坡发生前后监测点HF10的改进型切线角计算结果见表 2,基准误差改正前仅7月17日改进型切线角大于87°,而改正后从7月16日开始切线角均大于87°。可得出结论:若不对监测序列进行基准误差改正,会导致橙色和红色预警延迟5 d发布,对预警结果的可靠性产生影响。
| 日期 | 改正前/(°) | 改正后/(°) |
| 2020-07-12 | 85.99 | 86.71 |
| 2020-07-13 | 84.70 | 85.64 |
| 2020-07-14 | 85.65 | 86.43 |
| 2020-07-15 | 85.28 | 86.12 |
| 2020-07-16 | 86.81 | 87.38 |
| 2020-07-17 | 86.92 | 87.47 |
| 2020-07-18 | 87.31 | 87.80 |
| 2020-07-19 | 86.77 | 87.35 |
| 2020-07-20 | 86.22 | 86.89 |
| 2020-07-21 | 78.77 | 80.74 |
| 2020-07-22 | 75.63 | 78.12 |
3 结论
针对基准站出现电源不足等导致长时间停止工作,无法继续为监测站提供高精度数据服务的问题,本文提出切换其他监测站为新基准站的方法以保障监测的连续性和可靠性,同时顾及新基准站的运动状态及不稳定性,具有较高的工程应用价值。主要成果总结如下:
(1) 当基准站数据中断时,本文提出切换监测站为新基准站的方法。针对切换基准站后会产生的基准误差问题,本文通过分析基准站切换及基准站不稳定对监测结果的影响,给出一种顾及基准站运动状态特性的基准误差改正方法。
(2) 成功应用该方法对甘肃黑方台GNSS滑坡监测进行基准站切换,提高了监测结果的连续性及可靠性。与真实变形相比,改正后E、N、U 3个方向的RMSE分别为0.7、0.9和1.5 mm,满足滑坡监测的需求。
(3) 基于黑方台监测区域2020年7月20日发生滑坡的监测序列,以改进型切线角为预警判据评价基准站切换与基准误差改正对滑坡预警结果的影响,不进行基准误差改正可能导致预警的误判。
| [1] |
文海家, 张永兴, 柳源. 滑坡预报国内外研究动态及发展趋势[J]. 中国地质灾害与防治学报, 2004, 15(1): 1-4, 16. WEN Haijia, ZHANG Yongxing, LIU Yuan. A home and abroad investigative-tendency of landslide forecast[J]. The Chinese Journal of Geological Hazard and Control, 2004, 15(1): 1-4, 16. |
| [2] |
LIU Guang, ZBIGNIEW P, STEFANO S, et al. Land surface displacement geohazards monitoring using multi-temporal InSAR techniques[J]. Journal of Geodesy and Geoinformation Science, 2021, 4(1): 77-87. |
| [3] |
王桂杰, 谢谟文, 邱骋, 等. D-INSAR技术在大范围滑坡监测中的应用[J]. 岩土力学, 2010, 31(4): 1337-1344. WANG Guijie, XIE Mowen, QIU Cheng, et al. Application of D-INSAR technique to landslide monitoring[J]. Rock and Soil Mechanics, 2010, 31(4): 1337-1344. |
| [4] |
TOMÁS R, LI Zhenhong. Earth observations for geohazards: present and future challenges[J]. Remote Sensing, 2017, 9(3): 194-204. DOI:10.3390/rs9030194 |
| [5] |
YANG Yuanxi, GAO Weiguang, GUO Shuren, et al. Introduction to BeiDou-3 navigation satellite system[J]. Journal of the Institute of Navigation, 2019, 66(1): 7-18. DOI:10.1002/navi.291 |
| [6] |
王潜心, 徐天河, 许国昌. 自适应换站算法及其在长距离机载GPS动态相对定位中的应用[J]. 测绘学报, 2011, 40(4): 429-434. WANG Qianxin, XU Tianhe, XU Guochang. Adaptively changing reference station algorithm and its application in GPS long range airborne kinematic relative positioning[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 429-434. |
| [7] |
DU Yuan, HUANG Guanwen, ZHANG Qin, et al. Asynchronous RTK method for detecting the stability of the reference station in GNSS deformation monitoring[J]. Sensors (Basel, Switzerland), 2020, 20(5): 1320. DOI:10.3390/s20051320 |
| [8] |
BAO Yan, GUO Wen, WANG Guoquan, et al. Millimeter-accuracy structural deformation monitoring using stand-alone GPS: case study in Beijing, China[J]. Journal of Surveying Engineering, 2018, 144(1): 05017007. DOI:10.1061/(ASCE)SU.1943-5428.0000242 |
| [9] |
王阅兵, 甘卫军, 陈为涛, 等. 北斗导航系统精密单点定位在地壳运动监测中的应用分析[J]. 测绘学报, 2018, 47(1): 48-56. WANG Yuebing, GAN Weijun, CHEN Weitao, et al. The analysis of precise point positioning of BeiDou navigation satellite system application in crustal motion monitoring[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(1): 48-56. DOI:10.11947/j.AGCS.2018.20170147 |
| [10] |
WANG Guoquan, KEARNS T J, YU Jiangbo, et al. A stable reference frame for landslide monitoring using GPS in the Puerto Rico and Virgin Islands region[J]. Landslides, 2014, 11(1): 119-129. DOI:10.1007/s10346-013-0428-y |
| [11] |
卞和方, 张书毕, 张秋昭, 等. 基于IGS跟踪站的大面积矿区GNSS变形监测[J]. 中国有色金属学报, 2014, 24(2): 514-519. BIAN Hefang, ZHANG Shubi, ZHANG Qiuzhao, et al. Monitoring large-area mining subsidence by GNSS based on IGS stations[J]. Transactions of Nonferrous Metals Society of China, 2014, 24(2): 514-519. |
| [12] |
姜晨光, 石伟南, 巩亮生, 等. 大坝变形GPS双基站自动监测系统设计与应用[J]. 大坝与安全, 2011(3): 29-32. JIANG Chenguang, SHI Weinan, GONG Liangsheng, et al. Design and application of dam deformation automatic monitoring system based on double basis stations GPS technique[J]. Dam & Safety, 2011(3): 29-32. |
| [13] |
WANG Guoquan, LIU Hanlin, MATTIOLI G, et al. CARIB18: a stable geodetic reference frame for geological hazard monitoring in the Caribbean region[J]. Remote Sensing, 2019, 11(6): 680. |
| [14] |
黄立人, 马青. 参考框架的一致性及其对形变分析的影响[J]. 地壳形变与地震, 2001, 21(2): 31-36. HUANG Liren, MA Qing. Consistency of reference frame and its influence on deformation analysis[J]. Crustal Deformation and Earthquake, 2001, 21(2): 31-36. |
| [15] |
陈鑫连. 动态大地测量[M]. 北京: 中国铁道出版社, 1994. CHEN Xinlian. Dynamic geodesy[M]. Beijing: China Railway Publishing House, 1994. |
| [16] |
杨元喜, 张丽萍. 坐标基准维持与动态监测网数据处理[J]. 武汉大学学报(信息科学版), 2007, 32(11): 967-971. YANG Yuanxi, ZHANG Liping. Maintenance of coordinate datum and data processing of dynamic monitoring network[J]. Geomatics and Information Science of Wuhan University, 2007, 32(11): 967-971. |
| [17] |
罗力. 三峡库区滑坡监测GPS统测构网研究及应用[D]. 武汉: 武汉大学, 2013. LUO Li. The study of the landslide monitoring network reconstruction within unified datum in the Three Gorges Reservoir area and its application[D]. Wuhan: Wuhan University, 2013. |
| [18] |
刘鸿飞, 肖玉钢, 邓连生, 等. GPS变形监测系统中基准站长期稳定性分析[J]. 大地测量与地球动力学, 2013, 33(1): 113-116, 122. LIU Hongfei, XIAO Yugang, DENG Liansheng, et al. Analysis of long-term stability of reference stations in GPS deformation monitoring system[J]. Journal of Geodesy and Geodynamics, 2013, 33(1): 113-116, 122. |
| [19] |
许强, 汤明高, 徐开祥, 等. 滑坡时空演化规律及预警预报研究[J]. 岩石力学与工程学报, 2008, 27(6): 1104-1112. XU Qiang, TANG Minggao, XU Kaixiang, et al. Research on space-time evolution laws and early warning-prediction of landslides[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(6): 1104-1112. |
| [20] |
王利, 张勤, 黄观文, 等. GPS PPP技术用于滑坡监测的试验与结果分析[J]. 岩土力学, 2014, 35(7): 2118-2124. WANG Li, ZHANG Qin, HUANG Guanwen, et al. Experiment results and analysis of landslide monitoring by using GPS PPP technology[J]. Rock and Soil Mechanics, 2014, 35(7): 2118-2124. |
| [21] |
KONG Jiaxu, ZHUANG Jianqi, ZHAN Jiewei, et al. A landslide in Heifangtai, northwest of the Chinese Loess Plateau: triggered factors, movement characteristics, and failure mechanism[J]. Landslides, 2021, 18(10): 3407-3419. |
| [22] |
黄观文, 黄观武, 杜源, 等. 一种基于北斗云的低成本滑坡实时监测系统[J]. 工程地质学报, 2018, 26(4): 1008-1016. HUANG Guanwen, HUANG Guanwu, DU Yuan, et al. A lowcost real-time monitoring system for landslide deformaion with BeiDou cloud[J]. Journal of Engineering Geology, 2018, 26(4): 1008-1016. |
| [23] |
白正伟, 张勤, 黄观文, 等. "轻终端+行业云"的实时北斗滑坡监测技术[J]. 测绘学报, 2019, 48(11): 1424-1429. BAI Zhengwei, ZHANG Qin, HUANG Guanwen, et al. Real-time BeiDou landslide monitoring technology of "light terminal plus industry cloud"[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(11): 1424-1429. DOI:10.11947/j.AGCS.2019.20190167 |
| [24] |
许强, 曾裕平, 钱江澎, 等. 一种改进的切线角及对应的滑坡预警判据[J]. 地质通报, 2009, 28(4): 501-505. XU Qiang, ZENG Yuping, QIAN Jiangpeng, et al. Study on a improved tangential angle and the corresponding landslide pre-warning criteria[J]. Geological Bulletin of China, 2009, 28(4): 501-505. |
| [25] |
许强, 彭大雷, 何朝阳, 等. 突发型黄土滑坡监测预警理论方法研究: 以甘肃黑方台为例[J]. 工程地质学报, 2020, 28(1): 111-121. XU Qiang, PENG Dalei, HE Chaoyang, et al. Theory and method of monitoring and early warning for sudden loess landslide: a case study at Heifangtai Terrace[J]. Journal of Engineering Geology, 2020, 28(1): 111-121. |



