2. 中国地质调查局水文地质环境地质调查中心, 河北 保定 071051;
3. 自然资源部地质环境监测工程技术创新中心, 河北 保定 071051;
4. 中国地质科学院地质力学研究所, 北京 100081
2. Center for Hydrogeology and Environmental Geology Survey, China Geological Survey, Baoding 071051, China;
3. Technology Innovation Center for Geological Environment Monitoring, MNR, Baoding 071051, China;
4. Institute of Geomechanics, Chinese Academy of Geological Sciences, Beijing 100081, China
滑坡是世界上地质灾害最严重的类型之一[1-2],受限于不同的地质环境条件,诸多影响因素会导致滑坡发生,预测滑坡变形及形变演化过程是一项艰巨且富有挑战的关键任务[3]。滑坡的演化过程是一个复杂的多种影响因素叠加的非线性过程[4],因此,利用滑坡长时间位移监测数据可以形象表示滑坡发生的非线性位移动态行为特征。对于滑坡监测预警及预测来说,滑坡位移预测是滑坡灾害监测预警系统的重要组成部分之一[5-6],如何设计行之有效的滑坡变形监测和预测方法,有助于了解滑坡灾害失稳过程及形变特征,有利于减少滑坡给人类生命财产安全和基础设施带来风险[7-8]。
滑坡发生运动最主要的外在特征体现在滑坡重点形变区域位移的不断变化,对滑坡位移变形开展实时动态监测和形变预测显得至关重要。研究人员对滑坡位移预测开展了诸多研究,将多种数学模型用于预测滑坡位移,主要包括历史经验模型、数学统计模型、非线性模型和综合耦合模型。
(1) 历史经验模型。通过开展现场滑坡实时监测和实验室室内模型试验来获取长期大量的滑坡不间断位移形变监测数据,主要的经验模型包括斋藤模型、Crosta和Agliardi模型[9-10]。
(2) 数学统计模型。通过数学统计方法设计滑坡位移预测模型。典型的数学统计模型包括灰色系统模型[11]、灰色位移矢量角模型[12]、基于斜坡斜率变化的滑坡预测模型[9]。
(3) 非线性模型。通过非线性理论,包括突变理论[13]和协同理论[14],此类模型包括传统方式的非线性模型[15-16]、支持向量回归模型[17]、BP和Elman神经网络模型[15, 18-21]。
(4) 综合耦合模型。近年来,综合多种机器学习的复杂模型被用于预测滑坡灾害,这些模型主要结合雨量、位移、库水位来进行滑坡预测。例如,基于移动平均线的自回归综合模型用于预测滑坡位移变形[22-23]。经验模态分解模型[24]和集成经验模态分解[19, 25],通过长时间序列基于LSTM模型来预测滑坡位移形变[26]。
综上所述,研究人员利用多种模型实现了对滑坡位移的形变预测,但是上述模型也存在一些不足和缺点。历史经验模型需要通过大量的真实数据或蠕变试验来验证模型的准确性,只有合适的应用场景滑坡位移才能得到较好的预测,因此经验模型具有严格的应用适用条件限制;统计学模型在一定程度上解决了一些物理机制相对复杂的滑坡形变,对于单个影响因素的滑坡监测效果较好,但是对多重影响因素的统计学模型并不能较好地解决问题;神经网络等非线性模型具有良好的预测性能,但是非线性模型存在收敛速度慢且容易陷入局部极小值问题。
综合耦合模型有助于从多个模型角度出发实现对滑坡位移预测,在一定条件下提高了滑坡位移预测的准确率,例如采用EEMD方法可以消除长时间监测数据存在的模态混合问题[25, 27],该方法根据监测数据本身的时间尺度特征进行数据分解,非常适用于各种数据趋势项的提取分解。通过EEMD方法进行分解来获取各个监测子序列的不同频率特征,利用EEMD方法可以探讨研究诱发滑坡位移发生变形的局部特征,探索蠕变性滑坡在降雨情况下是否会对滑坡的变形发生重要的影响作用,可以有效避免采用原始位移数据所遇到的非线性和随机性问题。支持向量回归(SVR)对于处理非线性数据具有很大的灵活性,利用SVR模型有助于解决非线性回归问题。基于以上分析,本文研究通过EEMD-SVR方法来构建滑坡位移预测模型,通过EEMD方法提取滑坡位移数据的趋势项和周期项,结合降雨诱发因素,通过SVR模型采用高斯核函数实现对滑坡位移监测数据的有效预测。
该模型参数设置方便灵活、易于实现且运算效率高,可以有效控制滑坡位移预测中非线性局部最小值导致的预测效果不佳等问题。本文以贵州水城区发耳镇尖山营滑坡为例,通过分析滑坡内部孕育发展运动过程和外部环境因素,综合考虑滑坡位移、降雨量和预测数据在内的长时间监测序列集来构建滑坡预测模型,通过建立预测模型性能评价指标,将预测结果与测试样本进行对比,再与Elman神经网络、支持向量机(SVR)模型分别对比分析,从而验证EEMD-SVR模型的有效性和准确性,实现对滑坡位移的精准预测,有效提高滑坡位移预测的准确率。
1 EEMD-SVR位移预测模型构建 1.1 集合经验模态分解(EEMD)文献[28]提出的本征模函数(intrinsic mode function,IMF)概念,认为任何时间序列都可以通过经验模态分解(empirical mode decomposition,EMD)方法分解为多个IMF和一个趋势量。该文献提出的基于筛分(sifting)算法的EMD得到的IMF分量存在模态混叠(mode mixing,MM)。模态混叠的出现不仅会导致错假的时频分布,也使IMF失去物理意义,还存在端点效应、筛分迭代停止标准等问题。文献[29]提出一种噪声辅助信号分析方法—集合经验模态分解(ensemble EMD,EEMD),主要目的是在原始序列中加入高斯白噪声信号以消除模态混叠现象。以裂缝传感器获取到的监测数据为例说明EEMD算法步骤[30]:假定传感器节点每次采集L个监测数据作为训练数据,设置长度为N的训练窗口,采用先进先出结构每次更新数据为ΔL个数据,xh(t)为第h个滑动窗口的数据。具体步骤如下。
(1) 在原始数据序列xh(t)中加入高斯白噪声信号n(t)为,得到新序列
 (1)
(1)
(2) 根据数据序列求解极大值点构成的上包络线(max0(t))和极小值点构成的下包络线(min0(t)),上、下包络线均值为mean0(t),数据序列减去均值曲线为
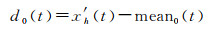 (2)
(2)
(3) 判断d0(t)是否满足IMF要求,若满足,则d0(t)为IMF;否则,记d0(t)为xh(t)重复步骤(1)—步骤(2)直至得到第1个IMF,记为c1(t)。
(4) 用新数据序列减去c1(t)为r1(t)=x′h(t)-c1(t)。以r1(t)为新的原始序列再通过步骤(1)—步骤(4)分析得到多组IMF,最终求得k阶IMF的包络数据为maxk(t)。
(5) 计算k阶IMF的上包络maxk(t)均值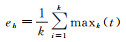
支持向量回归(support vector regression, SVR)是支持向量机(support vector machine, SVM)对回归问题的一种运用场景。SVM是一种基于统计学习VC维(Vapnik-Chervonenkis dimension)和结构风险最小化理论的监督学习分类技术,是一种二类分类模型,主要解决特征空间上间隔最大的线性分类问题,而对于线性不可分问题,利用核函数将低维数据映射到高维空间,从而将低维空间上的线性不可分问题转化为高维空间上的线性可分问题,通过求解再映射回到低维空间。
支持向量机可以有效解决小样本、非线性和高维数问题,并且能克服神经网络在处理非线性问题上的缺陷[24, 31],SVR通过SVM来对曲线进行拟合从而实现数据的回归分析。SVR主要操作步骤为:给定训练样本D,希望学得一个回归模型f(x)与y尽可能接近。其中
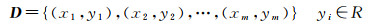 (3)
(3)
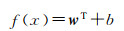 (4)
(4)
式中,w、b是待确定的参数。在这个模型中,只有当f(x)与y完全相同时,损失才为零,而支持向量回归假设能容忍的f(x)与y之间最多有ε的偏差,当且仅当f(x)与y的差别绝对值大于ε时,才计算损失,此时相当于以f(x)为中心,构建一个宽度为2ε的间隔带,若训练样本落入此间隔带,则被认为是预测正确的。
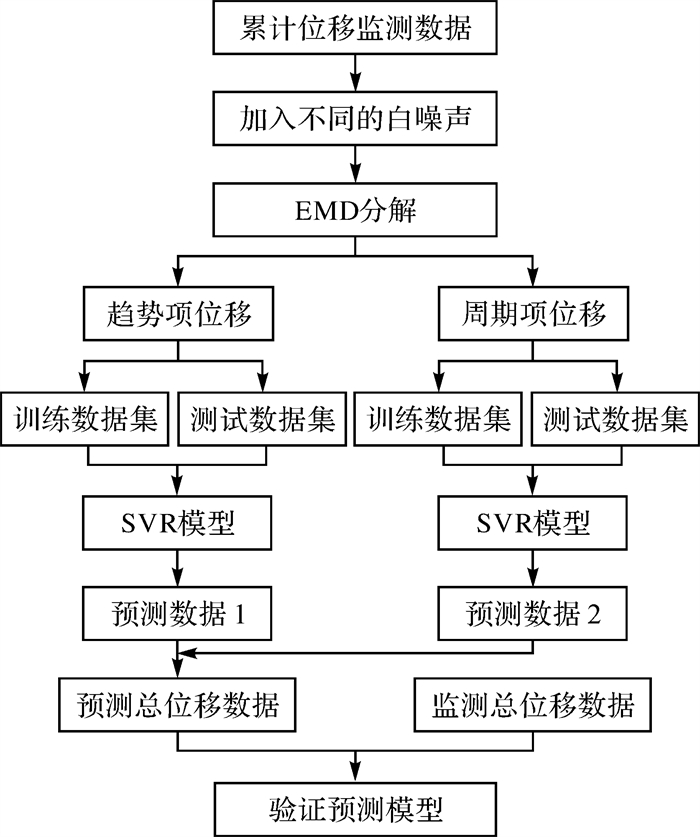
1.3 EEMD-SVR位移预测模型构建为了对发耳尖山营发生的滑坡位移进行详细分析,通过EEMD将位移监测数据分解为趋势项、周期项,考虑到滑坡位移发生的因素是多种原因导致,尤其考虑到降雨因素、人工扰动因素及地下采矿等外界因素,本文研究结合EEMD-SVR模型分别对位移的趋势项、周期项和位移累计监测数据分别做预测分析[32],方法流程图如图 1所示。
|
| 图 1 EEMD-SVR模型流程 Fig. 1 Flowchart of EEMD-SVR model |
1.4 位移预测模型性能评估
为了分析研究位移监测数据模型的预测能力,采用评估指数来分析位移预测性能,主要包括均方根误差(root mean squared error,RMSE)、平均绝对误差(mean absolute error,MAE)、平均绝对百分比误差(mean absolute percentage error,MAPE)、决定系数(coefficient of determination,R2)。
RMSE是预测值与位移监测数据真实值偏差的平方与样本数据n比值的平方根,计算公式为
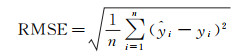 (5)
(5)
MAE是观测值与真实值的误差绝对值的平均值,计算公式为
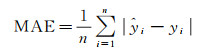 (6)
(6)
上述两个指数可以较好地反映预测模型的精确度,主要用来描述预测值与真实值的误差情况。
MAPE主要用来对预测方法的预测精度进行度量,通常以百分数表示准确性,计算公式为
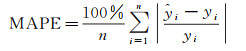 (7)
(7)
R2主要用来判断预测模型的好坏,其取值范围为[0, 1],R2越大,表示预测模型效果越好
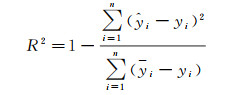 (8)
(8)
尖山营滑坡位于贵州省六盘水市水城区发耳镇西北部,地处贵州高原西部,地形跌宕起伏,切割强烈,属于构造侵蚀而成的低中山至中低山地貌。该滑坡在地形上表现为东南侧高,西北侧低;滑坡边界在平面上呈不规则的半圆形状,包括尖山营陡崖及其下方缓平台区,不稳定斜坡变形区前缘高程范围为1040~1120 m,后缘高程范围为1380~1502 m,高差约483 m,斜坡体后壁近于陡立,前缘坡度约63°。在该滑坡共部署5套监测设备,编号分别为EI19001—EI19005,采用LoRa+4G方式采集现场传感器数据,EI19001作为网关节点负责监测该滑坡区域内降雨量情况,此外还负责获取现场其他终端节点的裂缝传感器监测数据,EI19002—EI19005作为终端节点负责监测该滑坡区域内4处关键地表裂缝的变化情况,监测设备部署示意如图 2所示。

|
| 图 2 监测设备部署 Fig. 2 Deployment diagram of monitoring equipment |
2.2 滑坡监测数据
4个裂缝位移监测点分别设置在滑坡主要裂缝形变区域,通过LoRa无线自组网通信方式准确可靠地获取滑坡监测数据,分别设置低功耗变频工作模式和采集触发工作模式,低功耗变频工作模式时,微处理器主频由16 MHz降至65 KHz,设备功能模块定时上传监测数据;采集触发工作模式时,微处理器打开实时监听模式实时监测裂缝变化情况,一旦超过预定阈值即可启动数据通信接口上传位移监测数据。
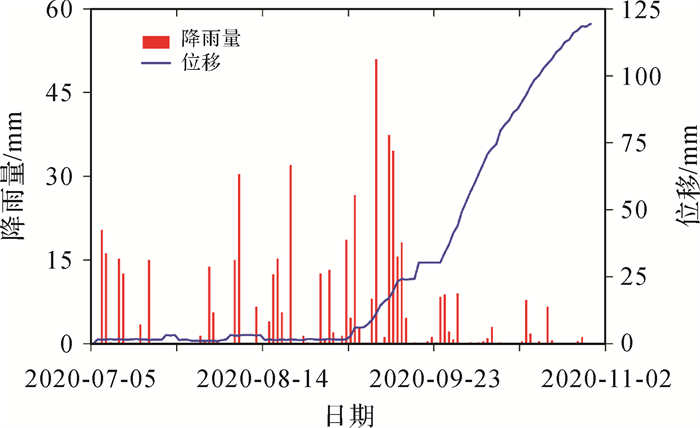
本文选取2020年7月6日—2020年10月30日的监测数据开展分析研究。初步设置系统的工作模式为定时回传间隔为1 h一条,同时开启数据采集端口触发回传模式,雨量触发回传阈值设为0.2 mm,位移触发回传阈值设为20 mm。雨量、裂缝位移综合分析曲线图如图 3所示。为了探究降雨量与滑坡裂缝位移变化的响应关系,以降雨周期内位移变化作为数据的研究样本,通过构建训练集和测试集来分别预测在有降雨和无降雨情况下位移的变化情况。
|
| 图 3 雨量和位移综合分析曲线 Fig. 3 Comprehensive analysis curve of rainfall and displacement |
2.3 EEMD-SVR滑坡位移预测模型
在EEMD-SVR模型中,主要利用EEMD方法将滑坡累计位移分解为趋势项和周期项[33-34],通过对滑坡裂缝位移的变形特征分析,滑坡于2020年7月6日开始出现位移变形,故选取2020年7月6日—2020年10月30日的117 d监测数据开展数据分析,选取2020年7月6日—2020年10月10日的97 d监测数据作为训练集,选取2020年10月11日—2020年10月30日的20 d作为测试数据验证预测模型。考虑到影响滑坡位移变形主要包括滑坡内在条件和外界因素,趋势项代表滑坡长期内动力下的变形趋势,周期项代表滑坡可能受到外界降雨因素作用下的动力响应[32, 35]。
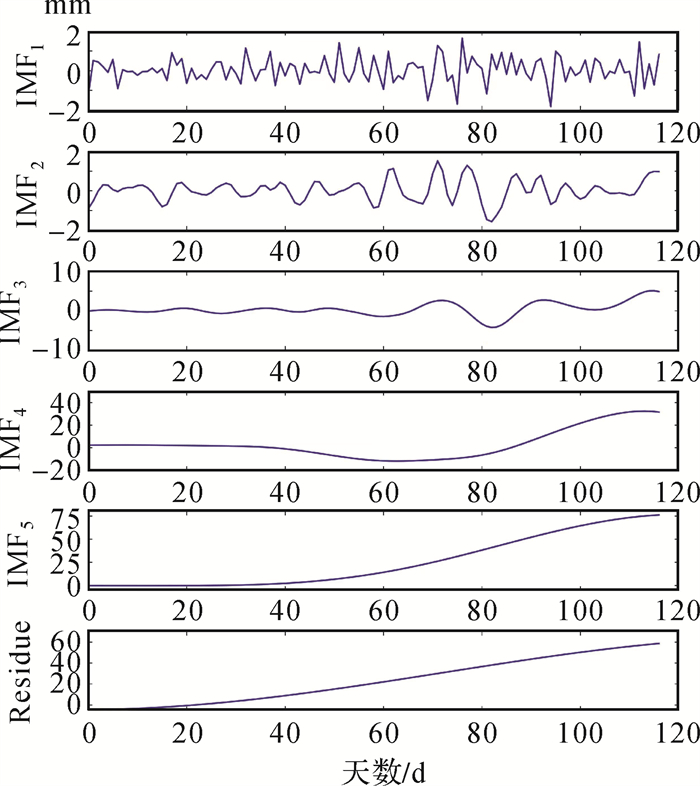
首先利用EEMD对滑坡累计位移进行分解,图 4代表EI19003设备累计位移分解后的趋势项和周期项。周期项位移主要发生在7~9月,也是滑坡所在区域的降雨季节,这表明周期项位移的变化可能受到了强降雨因素的影响。
|
| 图 4 位移时间序列EEMD分解结果 Fig. 4 EEMD decomposition results of displacement time series |
通过EEMD分解结果,观察到IMF1到IMF5波动频率依次降低,Residue为残余分量。由于IMF1—IMF3频率较高,波动幅度较小,可合并为滑坡位移的周期项,IMF4、IMF5相对较低,变化幅度相对较高,可以将IMF4和IMF5两项合并为滑坡位移的趋势项。严格意义上,EEMD分解结果的所有IMF之和并不等于原始位移,考虑到预测模型的准确性,在本文中规定趋势项=IMF4+IMF5,周期项=原始位移-趋势项。
然后设置SVR模型的输入变量,SVR模型输入参数主要包括核函数、惩罚因子C和宽度系数γ,本文选取核函数为“rbf”,通过网格搜索函数(gridSearchCV)多次训练得到最佳惩罚因子C=100、宽度系数γ=0.01。综合考虑滑坡内在条件和外界降雨因素,SVR输入变量的属性设置为前t1 d位移、前t2 d降雨量,输出为t d的位移。t1和t2根据实际预测效果再进行天数调优。例如,t1=2,t2=3时,表示输入变量为t1-1、t1-2 d位移和t2-1、t2-2、t2-3 d的降雨量。为了观察外界降雨因素对预测结果的影响,分别考虑有降雨量特征、无降雨量特征,连续预测1、10、20 d等6种情况下模型的预测情况。连续预测时采用滚动预测法,即将t时刻的预测位移作为t+1时刻的输入特征。
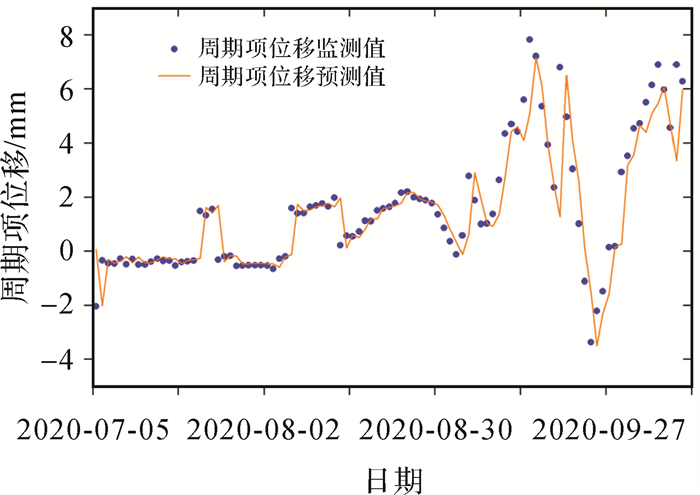
图 5、图 6分别为t1=4、t2=7时EEMD-SVR模型对位移周期项的训练和测试结果。
|
| 图 5 EEMD-SVR模型对位移周期项的训练结果 Fig. 5 Training results of the periodic component using EEMD-SVR model |

|
| 图 6 EEMD-SVR模型对滑坡位移周期项的预测结果 Fig. 6 Prediction results of the periodic component using EEMD-SVR model |
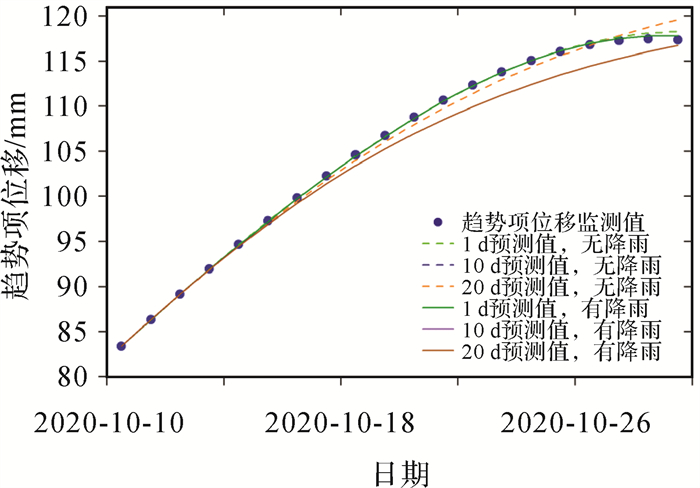
图 7、图 8分别为EEMD-SVR模型对位移趋势项的训练和测试结果。图 9为SVR模型对滑坡位移连续1、10、20 d情况下与原始位移的对比,由于连续滚动预测20 d包括连续预测10 d的数据,所以在曲线展示中连续10 d的预测曲线被隐藏在连续20 d的预测曲线中。

|
| 图 7 EEMD-SVR模型对位移趋势项的训练结果 Fig. 7 Training results of the trend component using EEMD-SVR model |
|
| 图 8 EEMD-SVR模型对位移趋势项的预测结果 Fig. 8 Prediction results of the trend component using EEMD-SVR model |
|
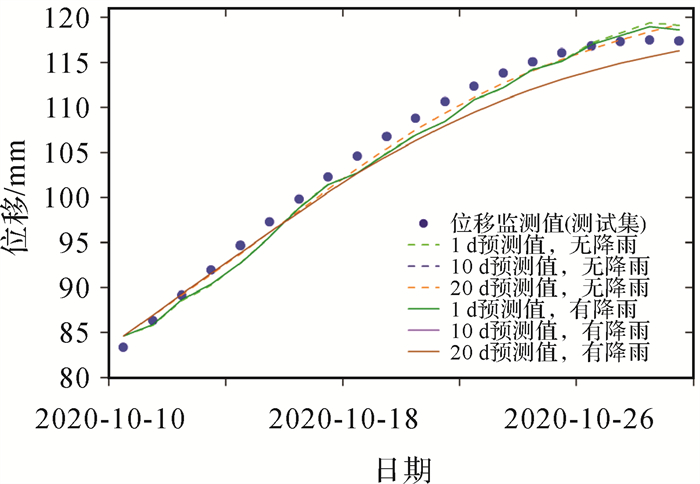
| 图 9 EEMD-SVR模型对位移测试集的预测结果 Fig. 9 Prediction results of displacement test set based on EEMD-SVR model |
通过观察滑坡整个数据集的预测结果(图 10)可知,EEMD-SVR模型表现出了比较好的拟合结果,误差相对更低,证明该机器学习模型的稳健性比较好。结果表明,EEMD-SVR机器学习模型能够准确预测尖山营滑坡的累积位移,具有较好的位移预测能力。

|
| 图 10 EEMD-SVR模型对整个数据集的预测结果 Fig. 10 Prediction results of total displacement set based on EEMD-SVR model |
通过性能指标评价对比分析(表 1),位移预测值与原始位移的绝对误差均可以控制在1%之内,基本可以反映出趋势项和周期项的变化趋势。考虑到噪声因素和模型训练的差异性,连续预测1、10、20 d在无降雨条件下相比降雨条件下RMSE、MAE、MAPE和R2均低于有降雨情况条件下,可以初步认为考虑降雨量因素情况下对模型预测影响较小,说明该滑坡在降雨情况下对滑坡裂缝位移的影响较小。
| 测试集误差 | RMSE/mm | MAE/mm | MAPE/(%) | R2 |
| 1 d无降雨 | 0.648 | 0.549 | 0.518 | 0.996 8 |
| 1 d有降雨 | 0.652 | 0.558 | 0.527 | 0.996 7 |
| 10 d无降雨 | 0.671 | 0.523 | 0.541 | 0.990 5 |
| 10 d有降雨 | 0.846 | 0.649 | 0.651 | 0.985 0 |
| 20 d无降雨 | 0.793 | 0.667 | 0.615 | 0.995 2 |
| 20 d有降雨 | 1.758 | 1.339 | 1.340 | 0.976 4 |
2.4 模型性能评估
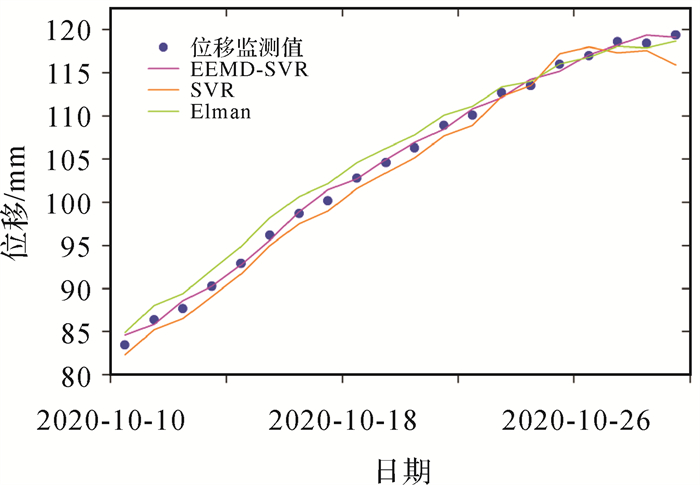
采用2020年尖山营滑坡在雨季汛期内的原始监测数据通过EEMD-SVR模型进行学习预测,为了评价其预测性能,利用1.4节中的性能指标来进行评价。在考虑有无降雨作用下,许多机器学习模型(如SVR和Elman)可以提供令人满意的预测性能[24, 36]。为了验证所提方法的有效性和科学意义,各种模型之间的准确性比较是至关重要的[37-38],各模型配置参数如下:EEMD-SVR和SVR模型中的惩罚因子C=100、宽度系数γ=0.01,Elman模型中的迭代次数maxgen=50、种群规模sizepop=40、交叉概率pcross=0.7、变异概率pmutation=0.01。图 11为2020年雨季汛期内无降雨条件下不同机器学习模型预测值与真实值的对比。
|
| 图 11 EEMD-SVR和SVR、Elman模型对原始位移与预测位移的对比分析 Fig. 11 Comparative analysis of EEMD-SVR, SVR and Elman models on original and predicted displacement |
表 2为EEMD-SVR和SVR、Elman模型的测试集预测性能的不同评价标准。本文由于涉及到的监测数据规模相对较小,结果表明,SVR和Elman模型在滑坡位移预测中表现出了一定的预测性能,但是经过EEMD分解之后的SVR模型比单一模型具有更好的预测性能,其预测结果更接近于原始位移监测值。由表 2可知,EEMD-SVR连续1 d预测测试集的RMSE是0.648 mm,MAPE是0.518%,均低于其他单一模型。说明EEMD-SVR模型在该类地形的位移预测表现更佳。总体而言,基于EEMD-SVR的综合耦合模型在该滑坡位移预测方面优于单一模型,具有较好的预测性能,可以满足一般的工程应用需求。
| 模型类型 | RMSE/mm | MAE/mm | MAPE/(%) | R2 |
| EEMD-SVR | 0.648 | 0.549 | 0.518 | 0.996 8 |
| SVR | 1.327 | 1.179 | 0.991 | 0.986 5 |
| Elman | 1.410 | 1.251 | 1.131 | 0.984 8 |
3 讨论和结论
本文选取贵州省岩溶山区一处典型滑坡为研究对象,通过对滑坡位移变形特征的分析,采用机器学习模型来预测滑坡位移的下一步变形趋势,该模型基于EEMD分解和SVR模型,预先考虑滑坡位移的动态变化可能会受到降雨季节的影响,通过EEMD将滑坡累计位移分为趋势项和周期项,然后利用SVR模型分别对趋势项和周期项进行了预测分析,然后将两个分量之和计为滑坡累计总的预测位移。选取前t1 d位移、前t2 d降雨量作为SVR模型的输入向量,分别预测在有降雨因素和无降雨因素下周期项和趋势项的位移变形情况。
利用尖山营滑坡2020年雨季汛期内的位移监测数据,通过滑坡后20 d位移数据对模型进行验证分析。通过预测结果表明,EEMD-SVR模型能够准确预测滑坡位移变形情况,通过性能评价指标可以做出初步判断,该滑坡在长期内在条件作用下,短时间内可能受降雨因素滑坡位移发生变化,但降雨因素对于长期位移预测影响较小。基于EEMD-SVR的综合耦合模型表现均优于其他单一模型,对比其他传统的机器学习算法,EEMD-SVR模型可以深入了解滑坡位移变形与降雨量之间的关联关系,对分析滑坡位移变形提供了可靠稳定的技术手段,说明EEMD-SVR模型在该滑坡的位移预测表现更佳。同时,EEMD-SVR模型有较好的适用性和稳健性,算法稳定、解算效率高、性能突出、误差较小,可以满足工程实践需要。EEMD-SVR模型结果表明,由于滑坡的动态变形过程会受到内外因素的综合影响,对不同影响因素采用不同的模型可以有效提高滑坡变形的预测精度。因此,在以后的工作中应将引入其他更多的影响因素加入模型研究中,以此来进一步提高滑坡位移预测的准确度和精确度。
| [1] |
ZHU Xing, XU Qiang, TANG Minggao, et al. Comparison of two optimized machine learning models for predicting displacement of rainfall-induced landslide: a case study in Sichuan province, China[J]. Engineering Geology, 2017, 218: 213-222. DOI:10.1016/j.enggeo.2017.01.022 |
| [2] |
SEGONI S, PICIULLO L, GARIANO S L. A review of the recent literature on rainfall thresholds for landslide occurrence[J]. Landslides, 2018, 15(8): 1483-1501. DOI:10.1007/s10346-018-0966-4 |
| [3] |
SEGONI S, PICIULLO L, GARIANO S L. Preface: landslide early warning systems: monitoring systems, rainfall thresholds, warning models, performance evaluation and risk perception[J]. Natural Hazards and Earth System Sciences, 2018, 18(12): 3179-3186. DOI:10.5194/nhess-18-3179-2018 |
| [4] |
MIAO Shengjun, HAO Xin, GUO Xuelian, et al. Displacement and landslide forecast based on an improved version of Saito's method together with the Verhulst-grey model[J]. Arabian Journal of Geosciences, 2017, 10(3): 53. DOI:10.1007/s12517-017-2838-y |
| [5] |
YIN Yueping, WANG Hongde, GAO Youlong, et al. Real-time monitoring and early warning of landslides at relocated Wushan town, the Three Gorges Reservoir, China[J]. Landslides, 2010, 7(3): 339-349. DOI:10.1007/s10346-010-0220-1 |
| [6] |
VAN KHOA V, TAKAYAMA S. Wireless sensor network in landslide monitoring system with remote data management[J]. Measurement, 2018, 118: 214-229. DOI:10.1016/j.measurement.2018.01.002 |
| [7] |
CORSINI A, MULAS M. Use of ROC curves for early warning of landslide displacement rates in response to precipitation (Piagneto landslide, Northern Apennines, Italy)[J]. Landslides, 2017, 14(3): 1241-1252. DOI:10.1007/s10346-016-0781-8 |
| [8] |
LIU Junqi, TANG Huiming, LI Qi, et al. Multi-sensor fusion of data for monitoring of Huangtupo landslide in the Three Gorges Reservoir (China)[J]. Geomatics, Natural Hazards and Risk, 2018, 9(1): 881-891. DOI:10.1080/19475705.2018.1478892 |
| [9] |
MUFUNDIRWA A, FUJⅡ Y, KODAMA J. A new practical method for prediction of geomechanical failure-time[J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(7): 1079-1090. DOI:10.1016/j.ijrmms.2010.07.001 |
| [10] |
HEGDE J, ROKSETH B. Applications of machine learning methods for engineering risk assessment-a review[J]. Safety Science, 2020, 122: 104492. DOI:10.1016/j.ssci.2019.09.015 |
| [11] |
邓聚龙. 灰色数理资源科学导论[M]. 武汉: 华中科技大学出版社, 2010. DENG Julong. Introduction to grey mathematical resource science[M]. Wuhan: Huazhong University of Science & Technology Press, 2010. |
| [12] |
殷坤龙, 晏同珍. 滑坡预测及相关模型[J]. 岩石力学与工程学报, 1996, 15(1): 1-8. YIN Kunlong, YAN Tongzhen. Landslide prediction and relevant models[J]. Chinese Journal of Rock Mechanics and Engineering, 1996, 15(1): 1-8. |
| [13] |
秦四清. 斜坡失稳过程的非线性演化机制与物理预报[J]. 岩土工程学报, 2005, 27(11): 1241-1248. QIN Siqing. Nonlinear evolutionary mechanisms and physical prediction of instability of planar-slip slope[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(11): 1241-1248. DOI:10.3321/j.issn:1000-4548.2005.11.001 |
| [14] |
KUMAR S, RANGAN P V, RAMESH M V. Design and validation of wireless communication architecture for long term monitoring of landslides[M]//MIKOŠ M, ARBANAS Ž, YIN Y P, et al. Advancing Culture of Living with Landslides. Cham: Springer, 2017: 51-60.
|
| [15] |
DU Juan, YIN Kunlong, LACASSE S. Displacement prediction in colluvial landslides, Three Gorges Reservoir, China[J]. Landslides, 2012, 10(2): 203-218. |
| [16] |
YAO Wei, ZENG Zhigang, LIAN Cheng, et al. Training enhanced reservoir computing predictor for landslide displacement[J]. Engineering Geology, 2015, 188: 101-109. DOI:10.1016/j.enggeo.2014.11.008 |
| [17] |
CAI Zhenglong, XU Weiya, MENG Yongdong, et al. Prediction of landslide displacement based on GA-LSSVM with multiple factors[J]. Bulletin of Engineering Geology and the Environment, 2016, 75(2): 637-646. DOI:10.1007/s10064-015-0804-z |
| [18] |
LIAN Cheng, ZENG Zhigang, YAO Wei, et al. Multiple neural networks switched prediction for landslide displacement[J]. Engineering Geology, 2015, 186: 91-99. DOI:10.1016/j.enggeo.2014.11.014 |
| [19] |
LIAN Cheng, ZENG Zhigang, YAO Wei, et al. Ensemble of extreme learning machine for landslide displacement prediction based on time series analysis[J]. Neural Computing and Applications, 2014, 24(1): 99-107. DOI:10.1007/s00521-013-1446-3 |
| [20] |
HUANG Faming, YIN Kunlong, ZHANG Guirong, et al. Landslide displacement prediction using discrete wavelet transform and extreme learning machine based on chaos theory[J]. Environmental Earth Sciences, 2016, 75(20): 1376. DOI:10.1007/s12665-016-6133-0 |
| [21] |
ELMAN J L. Finding structure in time[J]. Cognitive Science, 1990, 14(2): 179-211. DOI:10.1207/s15516709cog1402_1 |
| [22] |
MA Junwei, TANG Huiming, LIU Xiao, et al. Probabilistic forecasting of landslide displacement accounting for epistemic uncertainty: a case study in the Three Gorges Reservoir area, China[J]. Landslides, 2018, 15(6): 1145-1153. DOI:10.1007/s10346-017-0941-5 |
| [23] |
CARLÀ T, INTRIERI E, DI TRAGLIA F, et al. A statistical-based approach for determining the intensity of unrest phases at Stromboli volcano (Southern Italy) using one-step-ahead forecasts of displacement time series[J]. Natural Hazards, 2016, 84(1): 669-683. DOI:10.1007/s11069-016-2451-5 |
| [24] |
XU Shiluo, NIU Ruiqing. Displacement prediction of Baijiabao landslide based on empirical mode decomposition and long short-term memory neural network in Three Gorges area, China[J]. Computers & Geosciences, 2018, 111: 87-96. |
| [25] |
LIAN Cheng, ZENG Zhigang, YAO Wei, et al. Displacement prediction model of landslide based on a modified ensemble empirical mode decomposition and extreme learning machine[J]. Natural Hazards, 2013, 66(2): 759-771. DOI:10.1007/s11069-012-0517-6 |
| [26] |
YANG Beibei, YIN Kunlong, LACASSE S, et al. Time series analysis and long short-term memory neural network to predict landslide displacement[J]. Landslides, 2019, 16(4): 677-694. DOI:10.1007/s10346-018-01127-x |
| [27] |
DU Han, SONG Danqing, CHEN Zhuo, et al. Prediction model oriented for landslide displacement with step-like curve by applying ensemble empirical mode decomposition and the PSO-ELM method[J]. Journal of Cleaner Production, 2020, 270: 122248. DOI:10.1016/j.jclepro.2020.122248 |
| [28] |
HUANG N E, SHEN Zheng, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings og the Royal Society A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995. DOI:10.1098/rspa.1998.0193 |
| [29] |
WU Zhaohua, HUANG N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41. DOI:10.1142/S1793536909000047 |
| [30] |
柳治谱, 王勇. 基于无线传感器网络的坡面异常信号检测方法研究[J]. 传感技术学报, 2017, 30(10): 1536-1541. LIU Zhipu, WANG Yong. Research on method of slope abnormal signal detection based on wireless sensor network[J]. Chinese Journal of Sensors and Actuators, 2017, 30(10): 1536-1541. |
| [31] |
杨帆, 许强, 范宣梅, 等. 基于时间序列与人工蜂群支持向量机的滑坡位移预测研究[J]. 工程地质学报, 2019, 27(4): 880-889. YANG Fan, XU Qiang, FAN Xuanmei, et al. Prediction of landslide displacement time series based on support vector regression machine with artificial bee colony algorithm[J]. Journal of Engineering Geology, 2019, 27(4): 880-889. |
| [32] |
邓冬梅, 梁烨, 王亮清, 等. 基于集合经验模态分解与支持向量机回归的位移预测方法: 以三峡库区滑坡为例[J]. 岩土力学, 2017, 38(12): 3660-3669. DENG Dongmei, LIANG Ye, WANG Liangqing, et al. Displacement prediction method based on ensemble empirical mode decomposition and support vector machine regression: a case of landslides in Three Gorges Reservoir area[J]. Rock and Soil Mechanics, 2017, 38(12): 3660-3669. |
| [33] |
ZHANG Xun, LAI K K, WANG Shouyang. A new approach for crude oil price analysis based on empirical mode decomposition[J]. Energy Economics, 2008, 30(3): 905-918. |
| [34] |
GUO Zizheng, CHEN Lixia, GUI Lei, et al. Landslide displacement prediction based on variational mode decomposition and WA-GWO-BP model[J]. Landslides, 2020, 17(3): 567-583. |
| [35] |
刘人杰, 黄健, 剪鑫磊, 等. EEMD-GA-SVM模型在滑坡位移预测中的应用[J]. 人民长江, 2019, 50(11): 134-139. LIU Renjie, HUANG Jian, JIAN Xinlei, et al. Landslide deformation prediction based on EEMD-GA-SVM model[J]. Yangtze River, 2019, 50(11): 134-139. |
| [36] |
LI Huajin, XU Qiang, HE Yusen, et al. Prediction of landslide displacement with an ensemble-based extreme learning machine and copula models[J]. Landslides, 2018, 15(10): 2047-2059. |
| [37] |
LING Qing, ZHANG Qin, ZHANG Jing, et al. Prediction of landslide displacement using multi-kernel extreme learning machine and maximum information coefficient based on variational mode decomposition: a case study in Shaanxi, China[J]. Natural Hazards, 2021, 108(1): 925-946. |
| [38] |
ZHANG Yonggang, YANG Lining. A novel dynamic predictive method of water inrush from coal floor based on gated recurrent unit model[J]. Natural Hazards, 2021, 105(2): 2027-2043. |



