2. 自然资源部大地测量数据处理中心, 陕西 西安 710054;
3. 地理信息工程国家重点实验室, 陕西 西安 710054
2. Geodetic Data Processing Centre of Ministry of Natural Resources, Xi'an 710054, China;
3. State Key Laboratory of Geo-information Engineering, Xi'an 710054, China
全球导航卫星系统(GNSS)在生态环境监测、地质灾害预警、气象遥感、地壳形变识别等方面已经得到广泛应用,短时快速高精度的山区监测点高精度定位是GNSS高精度应用的关键问题之一[1-6]。我国是地质灾害多发的国家,山区约占国土面积的69%。山区观测环境恶劣,高度垂直方向梯度变化大,气象条件存在非平稳变化的特征。因此,对于大高差山区快速测量而言,气象变化对GNSS定位的影响是需要重点关注的问题之一[7-12]。GNSS星座的增多、信号质量的提高,为精密位置服务、高时效气象产品生成等提供了契机[13]。连续运行基准站网提供的各类高精度产品(如电离层、对流层、卫星轨道误差、卫星钟差等)可为高山区、大落差地壳监测提供各类误差改正支持。
GNSS精密数据处理中,对流层延迟是山区测量中重要的观测误差之一,对流层延迟改正的精细化处理是GNSS精密快速定位的前提[9-10, 14]。大量研究表明,GNSS定位精度尤其是垂直方向精度取决于观测时长。然而,高山区域恶劣环境下,峰顶观测时长应尽可能短。例如2005年珠穆朗玛峰高程测量中,峰顶GNSS观测时间不足1 h。短时GNSS观测网采用传统对流层延迟估计策略时,对流层延迟参数的估计值往往存在较大偏差,影响载波相位模糊度固定,导致定位结果存在偏差,尤其影响大地高的精度[15-19]。众所周知,区域高程分量与对流层延迟参数强相关,没有可靠的对流层延迟模型,GNSS观测的高程精度就会降低[20-21]。然而,高海拔山区往往缺少实测的气象资料,通常仅依靠经验对流层模型进行天顶对流层延迟(zenith tropospheric delay, ZTD)计算,但是经验模型的适应性往往存在较大问题[15, 17-20],尤其在大高差山区,GNSS监测点之间往往落差很大,对流层延迟差异也较大,仅依靠经验模型或采用差分观测都很难严密控制对流层延迟的影响。当然,通过增加观测时长可以提升对流层延迟估计精度,然而,大高差山区恶劣环境下增加观测时长,又为GNSS观测增添了难度。
国内外学者针对大高差地区GNSS观测对流层延迟误差影响进行了大量研究。文献[7]提出了适用于GNSS和VLBI的对流层延迟改正的VMF1模型,大量试验证明该模型同样适用于GNSS对流层延迟改正。文献[8]研究了赤道地区对流层效应在大高差情况下,折射率的显著变化影响了GPS定位的准确性。文献[9]研究了山区GPS定位精度不如平原地区的主要因素,结果表明,对流层延迟改正不足是最主要的影响因素。文献[10]通过对比,发现高山区GNSS的残余对流层延迟与高程强相关,近900 m的高差引起的残余对流层影响能造成6 cm左右的高程误差。文献[11]研究了残余对流层延迟与高差之间的联系,结果表明,测站间高差小于400 m、观测时长4 h情况下,对流层残余误差仍然会引起2 cm以上的垂直分量定位误差。通过引入1个对流层延迟参数,可以大大削弱对流层残余误差。文献[12]分析了山区高差较大时,对流层延迟对坐标和正高的影响,并利用差分GNSS和PPP技术确定了山顶位置的椭球高度。文献[13]对GGOS的天顶总延迟产品在全球范围内的精度进行了评估,将纠正后的GGOS-ZTD产品应用到PPP中,对高程方向的收敛速度改善尤为明显。文献[22]针对对流层建模中测站位置参数与剩余对流层参数的相关性问题,提出利用外部数值大气模式数据集估计对流层延迟。文献[23]研究了对流层延迟对高差较大的短基线时间序列的影响,结果表明,不估计对流层延迟会使高程方向时间序列出现虚假的季节性变化。文献[24]进一步探讨了基线两端高差对垂直定位精度的影响,试验结果表明,随着高差的增大,定位精度降低。
目前,针对小高差、长时间GNSS观测(24 h以上)的对流层影响研究较充分,但是缺乏对短时(1 h)大高差区域(近1000 m以上)观测网对流层影响的系统分析。如何在恶劣的大高差山区环境中,用尽可能短的观测时间,实现对流层延迟的有效改正十分重要。本文提出采用长时地面观测数据的位置和对流层延迟作为先验约束,代入短时同步双差观测方程中,减少方程中待估参数的维数,提高载波相位模糊度的固定效果,可以改善山顶点位坐标和对流层延迟参数估计精度。为综合验证先约束再估计对流层影响的有效性,本文分别从观测弧长(时间)和布网的基线间距(空间)两个方面进行了分析与验证。结果表明,采用先约束再估计残余对流层延迟的方法,可缩短恶劣条件的GNSS观测时长。
1 差分定位中的对流层延迟GNSS电磁波信号在传播过程中产生的大气误差主要是对流层延迟与电离层延迟。对流层延迟是由20 km以下的中性大气影响造成,电离层延迟受大约70~1000 km高度的传播介质影响,对流层延迟更易受水汽的运动情况及气候环境影响,且与传播信号频率无关。
当前,GNSS精密定位中对流层延迟处理策略主要采用以下4种方法:
(1) 不考虑对流层的影响,认为双差观测已经消除对流层延迟误差的影响,但当基线的距离增大或者站点间高差较大时,差分定位中的对流层延迟误差的影响仍然很显著,将影响载波相位整周模糊度的固定成功率[25],从而影响网解位置参数估计的质量和可靠性,目前该方法在大高差山区高精度定位中已不再使用。
(2) 直接采用对流层经验模型进行改正,主要有两种类型的模型:一种是基于实测气象资料构建的气象参数模型,主要有Blac模型、Hopfield模型及Sasstamonien模型等;另一种是非气象参数模型,主要有基于大气数值模式构建的GPT/GPT2/GPT2w模型、VMF1模型、IGGtrop模型等。
(3) 采用经典的参数估计法,将对流层湿延迟作为待估参数与位置参数一起求解。
(4) 采用外部修正法,利用外部的水汽辐射计或无线电探空设备采集高精度的对流层延迟作为参数的参考值进行修正。
通常,采用差分模式定位时,常采用参数估计的方法消除或者削弱对流层延迟的影响[26-30]。
1.1 相对对流层延迟误差相对对流层延迟误差是指两个测站之间的对流层延迟误差的差值。在高差相对较大的山区,相对对流层延迟偏差是影响测站高程的关键因素之一,而且该误差难以利用模型进行改正,对高程的误差影响公式为[31]
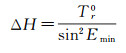 (1)
(1)
式中,Tr0为天顶相对对流层延迟误差;Emin为卫星截止高度角。由式(1)可知,当卫星截止高度角为10°时,1 mm的Tr0造成的高程误差为3.5 cm;当卫星截止高度角为5°时,1 mm的Tr0造成的高程误差高达13.2 cm。大量实践计算表明,参与差分解算的GNSS卫星的平均卫星截止高度角为30°左右,1 mm的Tr0造成的高程误差约为4 mm。
1.2 绝对对流层延迟误差绝对对流层延迟误差是指测站两端的相同对流层延迟误差,主要影响基线的尺度因子。尺度影响估算公式为
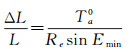 (2)
(2)
式中,L和ΔL分别为基线长度和基线误差;Ta0为绝对对流层延迟误差;Re为地球半径;Emin为卫星截止高度角。由式(2)可知,当卫星截止高度角为10°时,1 cm的Ta0造成基线尺度误差约为0.009×10-6。
2 顾及地面点对流层延迟约束的双差函数模型GNSS同步观测网采用双差模型进行基线解算时,如果采用无电离层组合,双差观测方程可表示为
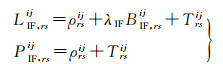 (3)
(3)
式中,上标i、j和下标r、s分别代表给定的卫星和接收机;LIF, rsij、PIF, rsij分别是测站r、s观测到卫星i、j的无电离层组合载波和伪距双差观测值;ρrsij为站星的双差几何距离;Trsij为双差对流层延迟;Irsij为双差电离层延迟;BIF, rsij为双差无电离层组合模糊度;λIF为无电离层组合观测量的波长。
假设地面点r的天顶对流层延迟参考值为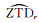
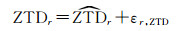 (4)
(4)
式中,εr, ZTD为地面点的天顶对流层延迟虚拟观测值的精度。由于地面点环境易于进行长时间GNSS观测,可获取高精度的地面点对流层延迟改正。因此,本文将εr, ZTD设置为地面点长时观测解算获取的对流层延迟及其方差作为先验值和先验精度。联合式(3)和式(4)进行参数估计,可求得基于地面点高精度对流层延迟先验约束的山顶对流层参数估计值。
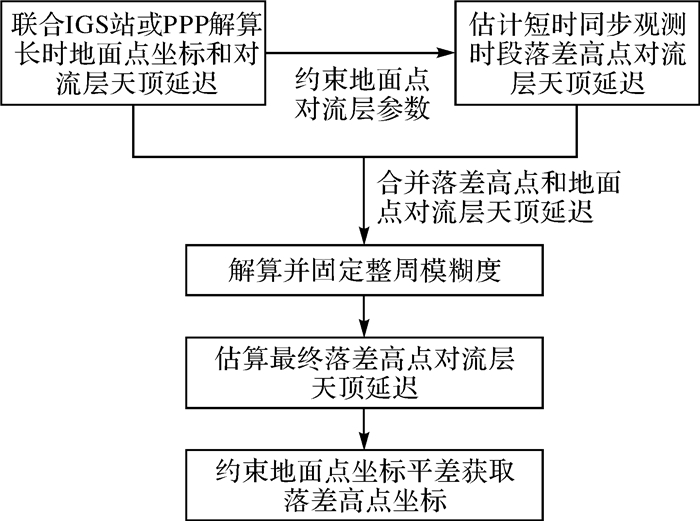
本文基于高精度GNSS定位软件Bernese 5.2实现快速定位解算。首先,解算地面点长时GNSS观测数据,获取高精度的定位结果和对流层延迟。其次,将高精度地面基站的先验对流层延迟信息(即上一步解算获取的地面基站的ZTD估计值和方差)和坐标作为先验信息,采用式(3)和式(4)联合解算,估计山顶点对流层延迟参数。然后,合并所有地面站与山顶站的对流层先验值进行约束,估计双差观测值的整周模糊度。最后,将固定的模糊度代入方程中,并给予地面点空间位置与天顶对流层延迟约束,实现双差方程的双约束解。该方法可有效减少待估参数的维数,调节法方程的病态性,从而达到提高大落差情况下山顶点的对流层延迟和定位结果的精度和可靠性。具体解算流程如图 1所示。
|
| 图 1 附加对流层约束的快速定位流程 Fig. 1 Flowchart of fast positioning with tropospheric delay constraint |
3 试验与分析
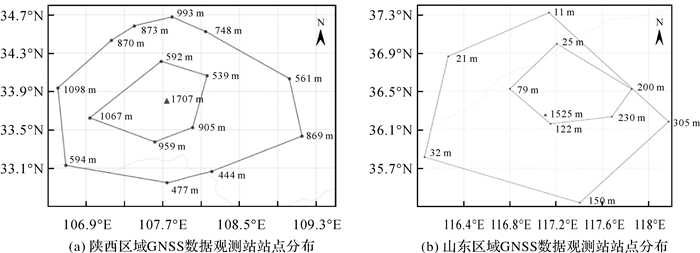
选取陕西区域和山东区域CORS网观测数据作为试验对象。陕西区域GNSS数据观测时间为2020年3月15日,观测时长为24 h,数据采样间隔为5 s,山顶站的高程超过1700 m,与选取的周围站点最大高差超过1200 m,平均高差为934 m,站点分布如图 2(a)所示。山东区域GNSS数据观测时间为2019年3月26日,观测时长为24 h,数据采样间隔为30 s,山顶站的高程超过1500 m,与选取的周围站点最大高差超过1500 m,平均高差为1407 m,站点分布如图 2(b)所示。为分析本文方法的时间与空间的适用性,将选取的地面基站按与山顶的距离远近分为两组,其中内圈基站相距山顶平均距离约为50 km,外圈基站相距山顶平均距离约为100 km。采用3种对流层延迟改正策略进行对比分析,具体解算方案如下。
|
| 图 2 站点分布 Fig. 2 Distribution of stations |
方案1:所有测站均不进行对流层延迟参数估计,对流层延迟误差的改正仅依靠对流层延迟改正模型的精度。对流层修正模型采用Saastamoinen模型值和VMF1模型值作为对流层延迟改正,即对流层参数计算时对流层干延迟、湿延迟采用Saastamoinen模型值,映射函数采用VMF1。
方案2:所有测站均进行对流层延迟估计,先验值采用Saastamoinen模型对流层干延迟,映射函数为VMF1,对流层湿延迟采用分段线性模型估计,时间间隔为1 h。
方案3:将地面点长时观测获取的对流层延迟和定位结果作为先验约束,估计山顶站点的对流层延迟与位置参数,对流层湿延迟采用分段线性模型估计,时间间隔为1 h。
由于对流层延迟受环境影响较大,本文从时间和空间两个方面分别验证本文方法的适用性,将数据分割成不同时长的短时观测数据,分别利用内圈和外圈基站及不同数量基站解算山顶站点天顶对流层延迟和三维空间坐标。同时,将24 h长时观测数据解算的最大高差基线的天顶相对对流层延迟与山顶点的定位结果作为参考值,计算短时解算结果与参考值之间的偏差,定量描述短时定位结果的天顶相对对流层延迟偏差的时空特性
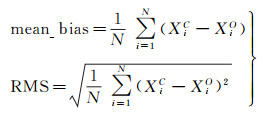 (5)
(5)
式中,XiC是由不同方案各时段估计的山顶位置与最大高差基线的相对对流层天顶延迟参数估计值;XiO为各时段估计的山顶位置与最大高差基线的对流层天顶延迟参数的真值;N表示参与统计的观测量总数;平均偏差mean_bias可衡量不同方案的偏离程度;均方根误差RMS可衡量解算策略的可靠性与稳定性。
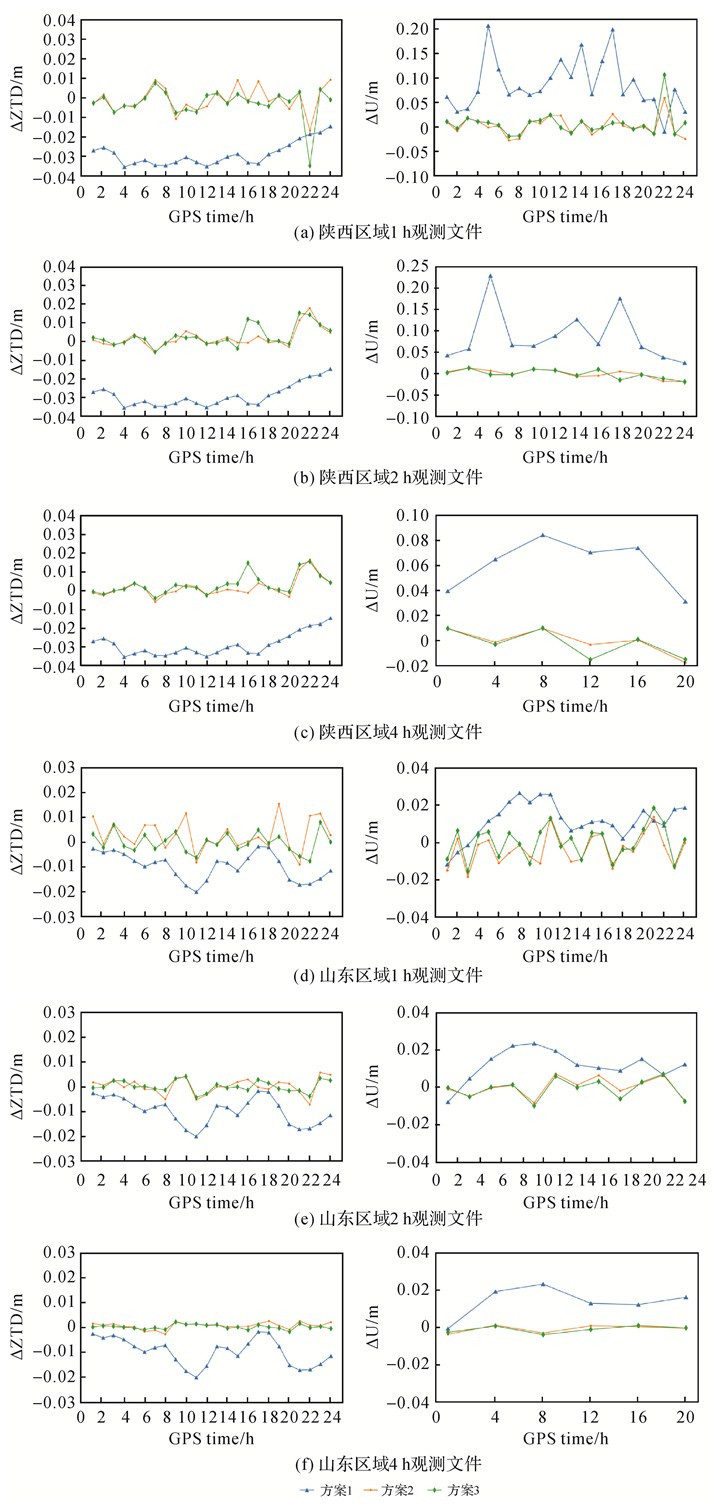
3.1 不同观测时长定位结果对比将内圈基站的观测数据分割为1、2和4 h的观测文件,分别采用以上3种方案对比定位效果,统计陕西区域和山东区域CORS站网的相对对流层延迟误差和大地高定位误差(图 3)。
|
| 图 3 内圈基站解算结果误差 Fig. 3 Solution errors by inner circle base station |
由图 3可知,方案1获取的相对对流层延迟参数存在较大的系统偏差,陕西区域偏差大于山东区域,说明VMF1对流层模型在山东区域的精度优于陕西区域。方案2与方案3天顶相对对流层偏差估计结果不存在明显的系统偏差,且随着观测时长的增长,山顶站点的大地高误差逐渐减小。陕西区域21∶00—22∶00时段误差较大的原因是山顶基站GNSS数据质量差导致相对对流层和定位结果较差,后续分析中该时段不参与计算。此外,相对对流层延迟误差与大地高结果表现为强相关;由于山顶与地面站的对流层延迟存在较大偏差,因此采用传统差分模型无法有效削弱对流层延迟误差。
方案1采用的VMF1模型在不同区域的误差不一致,VMF1对流层延迟模型的代表性误差会引入差分方程,导致山顶站点的大地高定位误差增大,因此,陕西区域解算结果中,部分时段误差超过20 cm。
方案2相对对流层延迟参数估算结果相对稳定,且随着观测时段的增长,相对对流层延迟误差逐渐减小,说明该方案的相对对流层延迟的解算精度与观测时长相关性强。多个时段的1 h短时观测解算的相对对流层误差超过1 cm,同时段的山顶站点的高程误差超过了2 cm。
方案3定位结果显示2 h和4 h观测数据的定位误差与方案2相当。如果以1 h观测数据进行解算,则方案3较方案2更为稳定,仅1个时段的相对对流层延迟误差超过1 cm,对应时段的大地高误差超过2 cm;随着观测时间的缩短,相对对流层延迟误差变化小,说明方案3能有效估计短时对流层延迟。
整周模糊度固定是GNSS高精度定位中的关键步骤,对流层延迟参数解的准确性也是制约模糊度固定的关键因素。为进一步分析对流层延迟估计方案对解算结果的影响,本文统计了不同方案的模糊度固定解的成功率(表 1)。
| 方案 | 陕西区域 | 山东区域 | |||||
| 1 h | 2 h | 4 h | 1 h | 2 h | 4 h | ||
| 方案1 | 86.22 | 89.21 | 87.90 | 72.53 | 75.95 | 75.53 | |
| 方案2 | 87.00 | 92.26 | 91.02 | 70.73 | 76.34 | 76.40 | |
| 方案3 | 91.39 | 93.08 | 91.30 | 73.76 | 77.94 | 78.12 | |
由表 1可知,方案3的基线模糊度固定解的成功率(平均值)是3种方案中最高的。1 h观测时长数据的解算结果表明,山东区域VMF1模型误差较小,方案1模糊度固定率优于方案2;随着观测时长的增加,方案2和方案3对流层延迟参数估计误差减小,模糊度固定解的成功率提高。
为进一步对比不同方案解算结果的可靠性,本文统计了1 h观测时长的山顶站点的N、E、U方向定位误差及对流层延迟估计结果误差(表 2、表 3)。
| 评价指标 | 方案1 | 方案2 | 方案3 | |||||||||||
| N | E | U | ZTD | N | E | U | ZTD | N | E | U | ZTD | |||
| RMS | 1.41 | 7.65 | 10.43 | 1.24 | 0.22 | 0.42 | 1.52 | 7.01 | 0.19 | 0.26 | 1.15 | 0.45 | ||
| mean_bias | -0.62 | 1.70 | 9.20 | 0.67 | -0.02 | 0.04 | 0.16 | -0.61 | 0.00 | -0.04 | 0.31 | -0.13 | ||
| 评价指标 | 方案1 | 方案2 | 方案3 | |||||||||||
| N | E | U | ZTD | N | E | U | ZTD | N | E | U | ZTD | |||
| RMS | 0.27 | 0.21 | 1.52 | 0.73 | 0.26 | 0.21 | 0.90 | 10.68 | 0.26 | 0.19 | 0.87 | 0.45 | ||
| mean_bias | 0.07 | 0.04 | 1.18 | -0.33 | 0.02 | -0.01 | -0.34 | -0.50 | 0.01 | 0.02 | 0.02 | 0.00 | ||
由表 2和表 3可知,常用对流层模型在不同地区精度不一致,而且很难利用模型控制对流层误差波动的影响,也不能通过增加观测时长消除对流层延迟参数的系统偏差,导致方案1的定位精度较差。
在估计对流层延迟时,方案2没有施加约束,地面站点的对流层延迟参数与山顶站点高程分量强相关,短时定位无法同时精确地解算出所有站点的对流层延迟参数,方案2的对流层延迟参数精度低于方案1。在山东区域的1 h短时解算结果中,方案2的定位精度略优于方案1。
方案3利用长时地面点计算出来的高精度对流层延迟作为先验约束,实现山顶站点短时同步双差对流层延迟参数的高精度估计,定位结果也较方案2更加稳定,定位精度更高,可满足短时高山测量的厘米级定位需求。
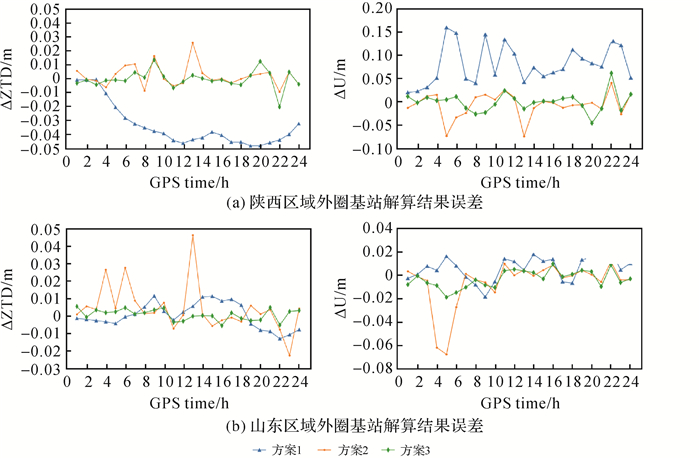
3.2 不同基线空间距离定位结果对比本文将外圈基站的观测数据分割为1 h的观测文件,对分时数据分别采用3种方案进行解算,对比内外圈基站解算的最大高差基线的相对天顶对流层延迟和山顶站点U方向定位误差(图 4)。
|
| 图 4 外圈基站解算结果误差 Fig. 4 Solution errors by outer circle base station |
对比图 3与图 4可知,随着观测网间的基站距离的增大,解算结果的稳定性均下降,方案3解算的精度和稳定性相较于方案1和方案2更优。统计不同方案的模糊度固定解的成功率和定位误差精度,结果见表 4—表 6。
| 方案 | 陕西区域 | 山东区域 |
| 方案1 | 84.40 | 72.14 |
| 方案2 | 87.23 | 69.16 |
| 方案3 | 89.05 | 72.62 |
| 评价指标 | 方案1 | 方案2 | 方案3 | |||||||||||
| N | E | U | ZTD | N | E | U | ZTD | N | E | U | ZTD | |||
| RMS | 1.61 | 6.49 | 8.97 | 1.24 | 0.38 | 1.53 | 2.68 | 5.16 | 0.21 | 0.67 | 1.18 | 0.50 | ||
| mean_bias | 0.01 | 1.11 | 7.99 | 0.67 | 0.07 | -0.04 | -0.94 | -0.49 | 0.00 | -0.13 | -0.02 | 0.01 | ||
| 评价指标 | 方案1 | 方案2 | 方案3 | |||||||||||
| N | E | U | ZTD | N | E | U | ZTD | N | E | U | ZTD | |||
| RMS | 0.33 | 0.27 | 1.14 | 0.73 | 1.55 | 2.55 | 2.03 | 3.06 | 0.24 | 0.45 | 0.78 | 0.39 | ||
| mean_bias | -0.01 | 0.00 | 0.58 | -0.33 | 0.44 | 0.18 | -0.64 | 0.71 | 0.09 | -0.05 | -0.30 | 0.08 | ||
由表 4—表 6可知,基站间的距离增大对方案1和方案2均有较大影响,方案3的解算结果受距离影响较小,同时方案3的模糊度固定解的成功率也是3种方案中最高的。方案2解算的ZTD误差明显减小,说明随着基线距离增加,对流层延迟参数与定位参数相关性降低。随着观测网基线距离的增加,方案3在点位精度、ZTD误差及模糊度固定解成功率上都具有较好的稳定度,也说明了该方案较其余两种方案在大落差高山区域高精度定位中具有一定优势。
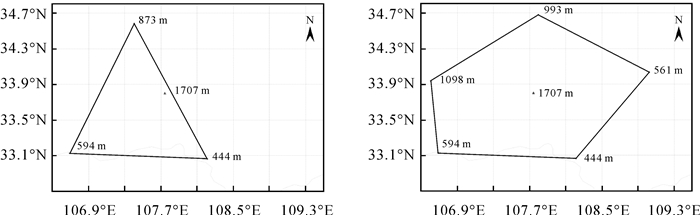
3.3 不同地面站点数量定位结果对比为了探究地面基站数量对于山顶定位的影响,获取地面站点数量和分布的最低配置,本文分别选取陕西区域3个和5个外圈基准站解算山顶点进行对比试验,站点分布如图 5所示。
|
| 图 5 不同数量基站的站点分布 Fig. 5 Distribution of stations of different number of base stations |
将不同外圈基站的观测数据分割为1 h的观测文件,对分时数据采用方案3进行解算,对比不同数量外圈基站解算结果精度,统计结果见表 7。
| 评价指标 | 3个基准站 | 5个基准站 | 10个基准站 | |||||||||||
| N | E | U | ZTD | N | E | U | ZTD | N | E | U | ZTD | |||
| RMS | 0.27 | 0.89 | 1.90 | 0.57 | 0.23 | 0.78 | 1.50 | 0.47 | 0.21 | 0.67 | 1.18 | 0.50 | ||
| mean_bias | -0.20 | -0.30 | -0.44 | 0.08 | -0.02 | -0.37 | -0.17 | 0.10 | 0.00 | -0.13 | -0.02 | 0.01 | ||
由表 7可知,随着基站数量增加,U方向的定位精度和ZTD解算精度均有提高,且山顶高程方向定位精度优于2 cm。平面方向定位精度与站点分布相关,增加站点数量可以提高解算结果的可靠性和稳定性。因此,方案3在大高差区域解算时,满足3个及以上的高精度地面基准站即可获取精度优于2 cm的山顶高程。
4 结语本文针对大高差短时双差网解中对流层延迟难以精确估计的难题,提出采用高山站点周围长时地面站点获取的高精度对流层延迟作为先验约束代入短时同步双差方程,进而估计山顶位置参数和对流层天顶延迟。
采用本文提出的方法与Saastamoinen+VMF1对流层模型改正、对流层延迟参数估计方法进行对比分析,结果表明,该方法在N、E、U方向的定位精度均优于传统方案,并且在U方向尤为明显。随着观测时段的缩短(1 h)和空间距离的增大(100 km以内),U方向的定位精度优于1.2 cm,且稳定性优于传统方案。具有先验约束的对流层延迟估计,有效控制了短时观测大落差基线两端对流层延迟不一致带来的高程误差影响。
从观测时长与空间距离特性来看,本文方法在保证精度与可靠性的基础上有效缩短了观测时长,拓展了观测网边长,克服了高山区域监测网布设等级与观测时长及站间距离的矛盾,满足山区短时高精度定位需求。
从大落差区域外围基准站的个数及图形分布对点位的影响分析可以得出:平面方向定位精度与站点分布相关,增加站点数据可以提高解算结果的可靠性与稳定性;区域周围满足3个及以上的高精度地面基准站时即可获取精度优于2 cm的山顶高程。
下一步将提升该方法的应用领域,利用CORS网解算大高差区域的高精度对流层延迟,实现山区高精度RTK定位。
| [1] |
BAO Yan, GUO Wen, WANG Guoquan, et al. Millimeter-accuracy structural deformation monitoring using stand-alone GPS: case study in Beijing, China[J]. Journal of Surveying Engineering, 2018, 144(1): 05017007. DOI:10.1061/(ASCE)SU.1943-5428.0000242 |
| [2] |
WANG Guoquan, LIU Hailin, MATTIOLI G S, et al. A stable geodetic reference frame for geological hazard monitoring in the Caribbean region[J]. Remote Senseing, 2019, 11(6): 680. DOI:10.3390/rs11060680 |
| [3] |
WANG G, WELCH J, KEARNS T J, et al. Introduction to GPS geodetic infrastructure for land subsidence monitoring in Houston, Texas, USA[C]//Proceedings of the 9th International Symposium on Land Subsidence. Nagoya, Japan: [s. n.], 2015: 297-303.
|
| [4] |
HASTAOGLU K O, SANLI D U. Accuracy of GPS rapid static positioning: application to Koyulhisar landslide, central Turkey[J]. Survey Review, 2011, 43(321): 226-240. DOI:10.1179/003962611X12894696205145 |
| [5] |
PAZIEWSKI J, SIERADZKI R, BARYLA R. Multi-GNSS high-rate RTK, PPP and novel direct phase observation processing method: application to precise dynamic displacement detection[J]. Measurement Science and Technology, 2018, 29(3): 035002-1-035002-15. |
| [6] |
张勤, 黄观文, 杨成生. 地质灾害监测预警中的精密空间对地观测技术[J]. 测绘学报, 2017, 46(10): 1300-1307. ZHANG Qin, HUANG Guanwen, YANG Chengsheng. Precision space observation technique for geological hazard monitoring and early warning[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1300-1307. DOI:10.11947/j.AGCS.2017.20170453 |
| [7] |
BOEHM J, WERL B, SCHUH H. Troposphere mapping functions for GPS and very long baseline interferometry from European Centre for Medium-Range Weather Forecasts operational analysis data[J]. Journal of Geophysical Research Solid Earth, 2006, 111(B2): B02406. |
| [8] |
DODO J D, KAMARUDIN M N, YAHYA M H. The effect of tropospheric delay on GPS height differences along the equator[J]. Surveying and Land Information Science, 2008, 68(3): 145-154. |
| [9] |
SATOMURA M, SHIMADA S, GOTO Y, et al. GPS measurements to investigate the reason why GPS is less accurate in mountain areas[C]//Proceedings of 2005 International Association of Geodesy Symposia. Berlin, Germany: Springer-Verlag, 2005: 44-47.
|
| [10] |
SCHÖN S, WIESER A, MACHEINER K. Accurate tropospheric correction for local GPS monitoring networks with large height differences[C]//Proceedings of the 18th ION GNSS International Technical Meeting of the Satellite Division. California, USA: [s. n.], 2005: 250-260.
|
| [11] |
安向东, 杨登科. 测站间高差对短时段GPS基线解算的影响[J]. 大地测量与地球动力学, 2016, 36(6): 534-538. AN Xiangdong, YANG Dengke. The impact of the height difference between stations on the baselines solution of short period GPS observations[J]. Journal of Geodesy and Geodynamics, 2016, 36(6): 534-538. |
| [12] |
AUH S C, LEE S B. Analysis of the effect of tropospheric delay on orthometric height determination at high mountain[J]. KSCE Journal of Civil Engineering, 2018, 22: 4573-4579. DOI:10.1007/s12205-018-0402-2 |
| [13] |
姚宜斌, 徐星宇, 胡羽丰. GGOS对流层延迟产品精度分析及在PPP中的应用[J]. 测绘学报, 2017, 46(3): 278-287. YAO Yibin, XU Xingyu, HU Yufeng. Precision analysis of GGOS tropospheric delay product and its application in PPP[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(3): 278-287. DOI:10.11947/j.AGCS.2017.20160383 |
| [14] |
BEUTLER G, BAUERSIMA I, GURTNER W, et al. Atmospheric refraction and other important biases in GPS carrier phase observations[M]. New South Wales: Australia Press, 1988.
|
| [15] |
DOERFLINGER E, BAYER R, CHÉRY J, et al. Le système de positionnement GPS en zone de montagne: effet de la troposphère sur la précision GPS verticale[J]. Comptes Rendus de l'Académie des Sciences, 1998, 326(5): 319-325. |
| [16] |
赵静旸, 时爽爽. 对流层天顶延迟模型研究进展及其在中国区域的精度分析[J]. 地球物理学进展, 2018, 33(1): 148-155. ZHAO Jingyang, SHI Shuangshuang. Research progress of zenith tropospheric delay model and its accuracy analysis over China[J]. Progress in Geophysics, 2018, 33(1): 148-155. |
| [17] |
LIU Jiye, CHEN Xihong, SUN Jize, et al. An analysis of GPT2/GPT2w+Saastamoinen models for estimating zenith tropospheric delay over Asian area[J]. Advances in Space Research, 2017, 59(3): 824-832. DOI:10.1016/j.asr.2016.09.019 |
| [18] |
姚翔, 陈明剑, 王建光, 等. 高纬度地区GPT2w模型的适应性分析[J]. 空间科学学报, 2020, 40(2): 242-249. YAO Xiang, CHEN Mingjian, WANG Jianguang, et al. Adaptability analysis of GPT2w model in high latitudes[J]. Chinese Journal of Space Science, 2020, 40(2): 242-249. |
| [19] |
ZHANG Di, GUO Jiming, CHEN Ming, et al. Quantitative assessment of meteorological and tropospheric zenith hydrostatic delay models[J]. Advances in Space Research, 2016, 58(6): 1033-1043. DOI:10.1016/j.asr.2016.05.055 |
| [20] |
王君刚, 陈俊平, 王解先, 等. 对流层经验改正模型在中国区域的精度评估[J]. 武汉大学学报(信息科学版), 2016, 41(12): 1656-1663. WANG Jungang, CHEN Junping, WANG Jiexian, et al. Assesment of tropospheric delay correction models over China[J]. Geomatics and Information Science of Wuhan University, 2016, 41(12): 1656-1663. |
| [21] |
蒋俊儒, 陶庭叶, 高飞. 一种提高大高差短基线精度的方法[J]. 大地测量与地球动力学, 2016, 36(4): 319-322. JIANG Junru, TAO Tingye, GAO Fei. A method for increasing precision of short baseline with large height difference by using semi-parametric model[J]. Journal of Geodesy and Geodynamics, 2016, 36(4): 319-322. |
| [22] |
YOUNES S A M, AFIFY H A. Accuracy improvement of tropospheric delay correction models in space geodetic data. case study: Egypt[J]. Geodesy and Cartography, 2014, 40(4): 148-155. |
| [23] |
王巍. 对流层延迟对高差较大GPS测站短基线时间序列的影响分析[J]. 大地测量与地球动力学, 2018, 38(5): 504-509. WANG Wei. Analysis on influence of tropospheric delay on short baseline time series from GPS stations with the large height difference[J]. Journal of Geodesy and Geodynamics, 2018, 38(5): 504-509. |
| [24] |
DU Sanli. Impact of large height difference on GPS vertical positioning solutions[C]//Proceedings of 2006 AGU Fall Meeting Abstracts. San Francisco, California, USA: [s. n.], 2006.
|
| [25] |
刘宁, 张永志, 熊永良. GPS参考站对流层湿延迟近实时估计的三步滤波算法[J]. 武汉大学学报(信息科学版), 2015, 40(7): 918-923. LIU Ning, ZHANG Yongzhi, XIONG Yongliang. A three-step Kalman filter algorithm for near real-time estimating tropospheric wet delay on GPS reference stations[J]. Geomatics and Information Science of Wuhan University, 2015, 40(7): 918-923. |
| [26] |
徐彦田, 程鹏飞, 蔡艳辉. 中长基线单基准站动态定位卡尔曼滤波算法[J]. 西南交通大学学报, 2013, 48(2): 317-322, 356. XU Yantian, CHENG Pengfei, CAI Yanhui. Kalman filter algorithm for medium-range real-time kinematic positioning with one reference station[J]. Journal of Southwest Jiaotong University, 2013, 48(2): 317-322, 356. |
| [27] |
张国利, 杨开伟, 时小飞, 等. 对流层改正模型在双差RTK解算中的精度影响分析[J]. 测绘通报, 2016(9): 149-150. ZHANG Guoli, YANG Kaiwei, SHI Xiaofei, et al. Analysis of the influence of troposphere correction model on the accuracy of double difference RTK solution[J]. Bulletin of Surveying and Mapping, 2016(9): 149-150. |
| [28] |
QIU Lei, LI Lei, LIU Zhixiang, et al. The correction model of tropospheric delay of GPS network RTK considering altitude factors[C]//Proceedings of 2009 International Conference on Information Engineering and Computer Science. Wuhan, China: IEEE, 2009: 1-4.
|
| [29] |
LI Wei, YUAN Yunbin, OU Jikun, et al. A new global zenith tropospheric delay model IGGtrop for GNSS applications[J]. Chinese Science Bulletin, 2012, 57(17): 2132-2139. |
| [30] |
FAN Haopeng, SUN Zhongmiao, ZHANG Liping, et al. A two-step estimation method of troposphere delay with consideration of mapping function errors[J]. Journal of Geodesy and Geoinformation Science, 2020, 3(1): 76-84. |
| [31] |
李凯锋, 欧阳永忠, 陆秀平, 等. 海道测量定位中对流层延迟差分估计技术研究[J]. 武汉大学学报(信息科学版), 2013, 38(8): 930-934. LI Kaifeng, OUYANG Yongzhong, LU Xiuping, et al. A differential estimation technique of troposphere delay for precise positioning in hydrographic surveying[J]. Geomatics and Information Science of Wuhan University, 2013, 38(8): 930-934. |



