2. 91937部队, 浙江 舟山 316002;
3. 92763部队, 辽宁 大连 116018
2. Troops 91937, Zhoushan 316002, China;
3. Troops 92763, Dalian 116018, China
随着世界各国对海洋探索的不断深入,人们对高精度海底地形的需求不断增加,当前水下地形获取的精细度及实时性仍须进一步提升。多波束测深系统作为当前海底地形测量最高效精准的装备之一,被广泛应用于世界各地的海底地形测量工作中。近年来,多波束测深原始数据量呈现爆发性增长[1-2],然而,长期以来高可信度的多波束测深异常值的清理工作多依赖于人工交互处理,存在处理周期较长的问题,极大地限制了数据处理的效率;现有自动处理算法虽然可以实现快速高效处理,但可信度达不到人工交互处理的水平,难以将其应用于面向海图制图的多波束测深数据处理[3-5]。因此,如何提高异常值自动清理算法处理结果的可信度是当前多波束测深数据处理领域亟待解决的一大难题。
经过多年研究,国内外已经产生大量成熟的异常值自动清理算法,其清理机制可以总结为以下3种方式:设置简单的门限阈值(如:深度、波束角、测深点之间的角度及梯度)[6-9]、基于统计学结果按条件筛选(如:中值、均值、水深值分布概率、不确定度)[10-15]及建立局部地形模型[16-18]。
以上传统算法,虽然都可以达到较好的清理效果,但大多受限于地形因素,且多数算法仅适用于清理离群粗差值这一种类型的异常值,尤其在地形复杂、数据质量较差的前提下,往往难以识别全部待清理的异常值。
随着机器学习算法的不断成熟,由于其在目标识别上所展现的独特优势,越来越多学者将其应用于多波束测深异常值的清理工作。文献[19]引入侵蚀和膨胀聚类算法,实现了深水区域多波束测深异常值的自动清理,该方法为多波束测深异常值提取提供了一种新颖的解决方法,但该算法仅仅基于整条测线的投影平面图进行聚类计算,没有考虑聚类窗口大小的变化,异常值容易被地形数据所掩盖。文献[20]将K-means聚类算法引入单脉冲测深数据的异常值检测,根据地形变化趋势将整ping划分为多个聚类窗口,以中央波束一定角度内的水深点为初始聚类样本,从中央波束向边缘不断聚类提取出代表真实地形的聚类簇,间接实现异常值的自动剔除,该方法较好地解决了识别精度问题,但由于K-means算法对噪点比较敏感,当存在大面积连续密集的深度异常及较大距离的数据缺失时,算法可能失效。以上两种基于聚类算法的清理方法能够相对准确地自动识别异常值,但均未实现离散异常值和集群化异常值的自动分类。离散异常值通常可以自动识别为无效数据,而集群化异常值中可能同时包含集群化粗差值与异常特征值,集群化粗差值应识别为无效数据,异常特征值应识别为可信数据。如果不将集群化异常值中的异常特征值单独标记出来,容易产生误判,导致处理结果存在低可信度风险的问题。当前,在集群化异常值中区分异常特征值和集群化粗差值多依赖于经验丰富的作业员,尚无很好的非人工解决方案。为此,本文基于密度聚类算法(density-based spatial clustering of applications with noise,DBSCAN),提出一种部分人工介入的异常值自动清理算法,即利用DBCSAN算法识别异常值,并将其分为无效和存疑两类,由此水深数据可分为可信、无效和存疑3类,保留可信数据、剔除无效数据,并将存疑数据提交人工判定有效性。该方法有效提高了异常值自动清理算法的可信度,同时避免了人工查询存疑数据耗费大量时间的问题,一定程度上提高了效率,较好地解决了自动清理算法效率高、可信度低而人工交互处理可信度高、效率低这一矛盾。
1 异常值的识别与分类 1.1 异常值的识别多波束测深过程中常伴随3种误差,即系统误差、随机误差及粗差,在为保障航行安全以及海图制图而进行的海道测量作业中,系统误差主要是指因仪器安装不准、声速校对错误等原因而产生的整体性误差,通过实际测量前良好的仪器校准及后处理中恰当的水深改正可以予以削弱;随机误差是指测量过程中因为仪器精度限制和环境因素影响等原因而产生的随机性误差,其误差值一般较小,包含在规范规定的测量精度范围内的随机误差可以保留;在排除以上两种误差影响的前提下,偏离于主要水深点集群的误差值可看作粗差, 精准识别并剔除粗差值是人工处理以及各种自动清理算法的主要目标[15]。为减少系统误差对试验结果的干扰,本文在研究过程中所采用的数据都已经过各项改正,系统误差的影响已降至最小。
当前人工交互处理大多基于后视图剔除异常水深值,后视图即将每一ping采集水深点投影到与航行方向垂直的平面上,通过多ping叠加形成。在人工交互处理过程中,操作人员主要依靠视觉密度大小识别异常值,视图中组成连续高密度区域的点集群据通常代表真实地形可识别为可信数据;孤立于连续高密度区域的其他数据点一般可识别为异常值。
1.2 异常值的分类有学者认为异常值只有一类,即所有处于统计学分布边缘的水深值[21],基于设置简单的门限阈值和基于统计学结果按条件筛选这两种方式所提出的多种算法都是基于以上的分类原则。然而,异常值占比通常浮动较大,在数据质量较好、地形平坦的区域,异常值占比可以低于1%[22];但在数据质量较差、地形复杂的区域,异常值占比最高可达25%[23]。面对如此复杂的占比率,此种分类方法很难准确地识别出所有异常值,同时难以进一步对异常值的可信度进行判定,故而难以克服可信度较低的问题。
由于真实存在的地形大多能够返回密集且连续的回波信号,因而可信数据应表现为连续的高密度点集群,异常值通常表现为离散点或者密度与规模相对较小的点集群,根据密度与几何特征可将异常值分为离散异常值点、结构化异常值集群和非结构化异常值集群3类。这一分类理论基于异常值在后视图中的图像特征,能够有效地识别定位异常值,但该分类方法未考虑异常值有效性问题,默认所有识别的异常值都是无效粗差值,应用于自动清理算法时存在一定弊端。结构化异常值集群和非结构化异常值集群中都有可能包含异常特征值,在自动清理过程容易产生误判。为此,本文认为应当从数据有效性角度对异常值进行重新分类,将异常值分为集群化异常值和离散异常值。结构化异常值集群、非结构化异常值集群以及上述分类方法未顾及的异常特征值集群,由于以上3种异常值的有效性难以自动判定,故本文将其共同归类为集群化异常值;由于离散异常值的有效性通常能够自动识别,故保留该异常值分类。综上所述,本文认为异常值应当分为离散异常值(图 1(b)、(d))、集群化异常值(图 1(a)、(c))两类,集群化异常值又包含集群化粗差值(图 1(c))和异常特征值(图 1(a)),异常值分类如图 2所示。
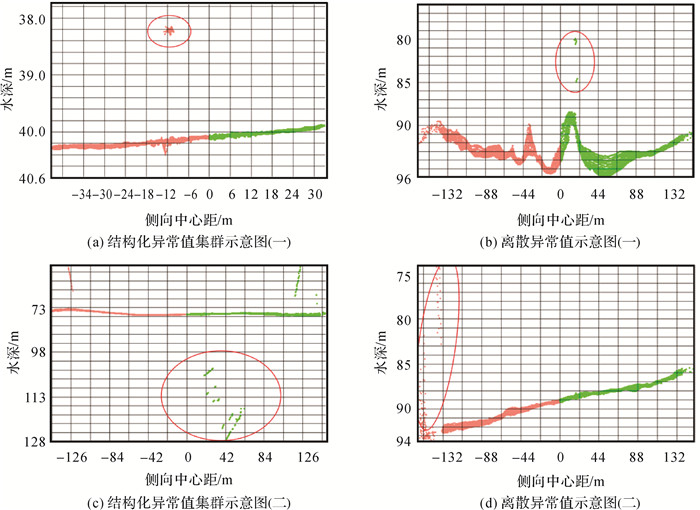
|
| 图 1 异常值图像特征示意 Fig. 1 Examples of outlier's geometries |
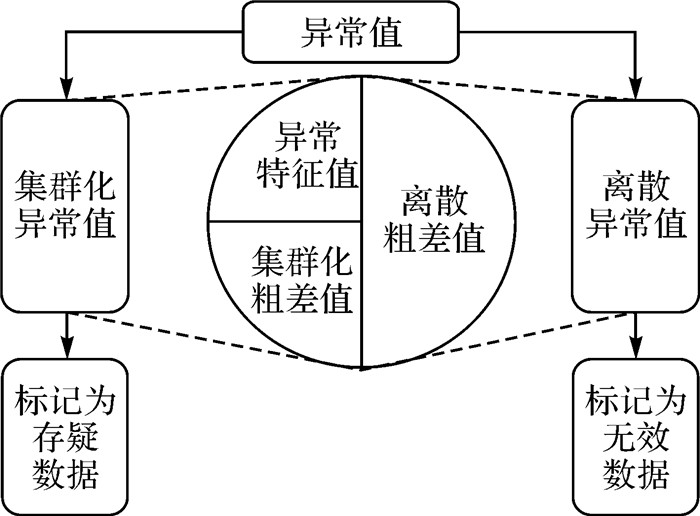
|
| 图 2 异常值分类示意 Fig. 2 Classification diagram of outliers |
2 密度聚类算法的基本原理
密度聚类算法(DBSCAN)是将n个d维数据样本聚集成k个类, 使同一类中样本的相似性最大, 而不同类中样本的相似性最小[24]。算法通过邻域半径(Eps)和邻域内点数阈值(MinPts)两个参数直接刻画出核心点的概念,当某点邻域半径内点的个数大于最少点数阈值时,该点即可视为核心点,并基于核心点及其领域内的点定义出直接密度可达、密度可达和密度相连3个概念[25],DBSCAN中点的密度关系如图 3所示。
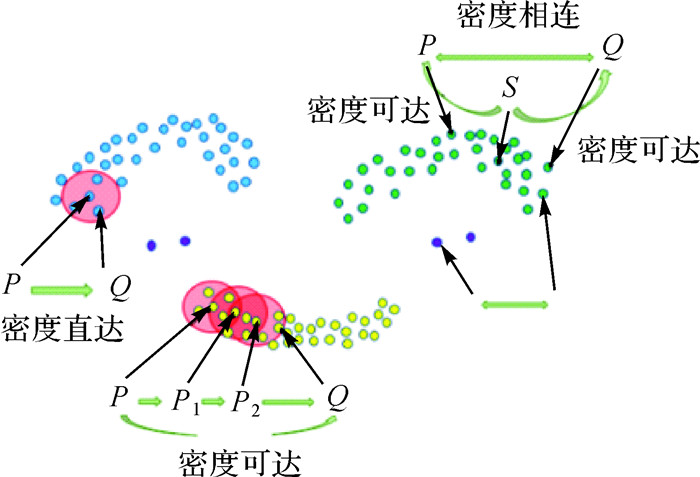
|
| 图 3 DBSCAN中点的密度关系 Fig. 3 Density relationship of points in DBSCAN |
(1) 核心点:如果存在点P,以P为圆心、Eps为半径构成邻域NEps(P),若该邻域中至少包含MinPts个样点,则点P是一个核心点。
(2) 直接密度可达:如果Q在P的邻域中, 并且P是核心对象,称Q由P直接密度可达。
(3) 密度可达:对于P和Q,如果存在一个序列P1, P2, …, Pn,其中P1=P, Pn=Q并且Pn+1由Pn直接密度可达,称Q由P密度可达。
(4) 密度相连:对于P和Q,如果存在S使P和Q均由S密度可达,则称P和Q密度相连,密度相连具有对称性。
聚类过程包含核心点搜索、初始核心点选取及聚类簇扩散3个主要步骤。首先,在待聚类数据集中搜索所有满足条件的核心点;然后,从任意一个核心点集群(核心点及其邻域半径内的点)开始,利用密度相连关系不断向未分类的点扩展直至无法继续,由此得到一个所有点都彼此密度相连的点集群,此点集群即可称为一个聚类簇,聚类簇内所有数据点标记为同一类;最后,继续查询是否还有未访问的核心点,开始新一轮聚类簇扩展,并继续形成新的聚类簇,直至所有核心点都被访问为止,剩余未被任何聚类簇吸纳的点将被标记为噪声。该算法能够有效识别彼此孤立的多个密集点集群,并将不能组成集群的离散点标记为噪声[26]。
海底地形通常是连续的,在多波束测深得到的水深数据中,真实地形数据通常反映为连续高密度点集群,异常值表现为孤立于连续高密度点集群的离散点或者点集群。因此,通过控制合理的聚类参数,DBSCAN算法能够有效区分真实地形数据与异常值;同时该算法可以更进一步有效地区分离散异常值与集群化异常值,进而能够有效地自动区分异常值中的存疑数据和无效数据,便于将存疑数据独立出来提交人工判定有效性,增强本文算法的可信度。
3 部分人工介入的异常值自动清理算法主要步骤本文算法如图 4所示:通过聚类算法将原始数据分为可信数据、无效数据和存疑数据3类,保留可信数据,剔除无效数据,并将存疑数据提交人工判定其有效性,最终将其归类为可信数据或者存疑数据。
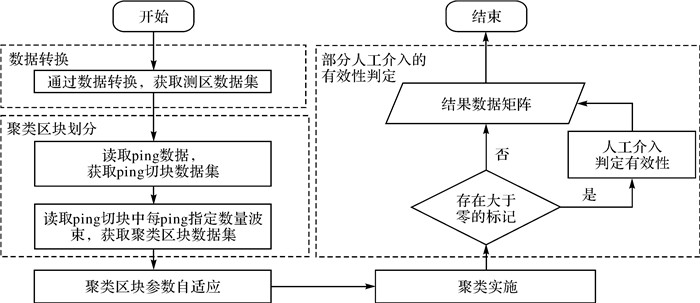
|
| 图 4 本文算法主要流程 Fig. 4 Flowchart of the main steps of the proposed algorithm |
3.1 基于密度聚类算法的水深数据分类
密度聚类算法能够将水深数据准确划分为可信、存疑和无效3类,该部分由4个主要步骤组成:数据转换、聚类区块划分、聚类参数自适应及聚类实施。
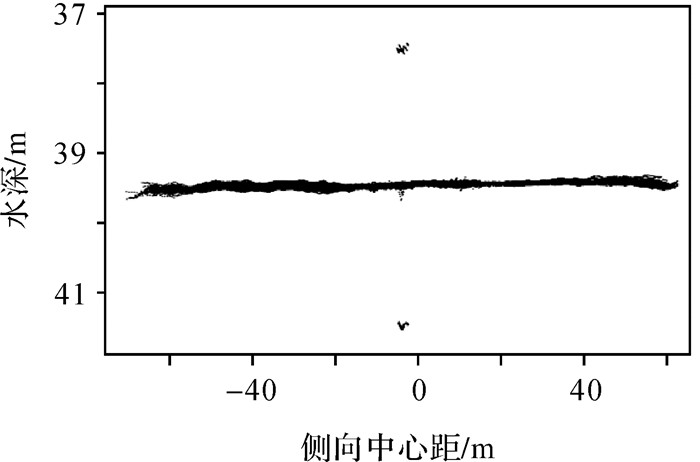
3.1.1 数据转换沿测量船航行方向将测点数据投影到垂直于航行方向的平面上,得到水深点后视图,即将三维点云数据(图 5)转化为以侧向中心距为横坐标、以水深值为纵坐标的二维数据(图 6)。应用式(1)将绝对坐标数据归算为以每ping中央波束为基准的侧向中心距离,生成聚类数据集,该数据集有2个维度数据,依次是侧向中心距离、水深值
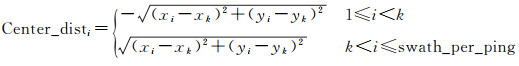 (1)
(1)
|
| 图 5 三维点云数据 Fig. 5 Point cloud data of 3D |
|
| 图 6 水深数据后视图 Fig. 6 Rear view of bathymetric data |
式中,Center_disti为多波束某一条带中第i个波束到中央波束的侧向中心距;xi、yi为第i个波束测点的绝对坐标;xk、yk为中央波束测点的绝对坐标;swath_per_ping为每ping包含的波束数。
3.1.2 聚类区块划分聚类区块即进行一次聚类所包含的测点数量,其大小是ping数规模值与窗口大小值的乘积。在多波束水深测量中,水深越深、波束越远离中央时,相邻两个波束之间的距离越大,相同半径的区域内所包含的水深点数越少,即水深点密度越小。为避免地形起伏及波束距离中央的远近对聚类准确性的影响,应当将整个测区划分为数个聚类区块,在每一个聚类区块中单独进行聚类。聚类区块的选择应根据地形特征,参考人工交互处理能够分辨出异常值的最小规模,地形复杂、数据较差的测区应当选取较小聚类区块,地形平坦、数据质量好的测区应当选择较大区块,合适的聚类区块大小主要通过以下两个参数来调节。
(1) ping数规模(ping_scale)。该参数表示当前聚类区块吸收的ping数,可控制聚类区块沿测量船航行方向的检测精度,前后相连的数个ping所测得的地形之间存在一定的关联性,但这种关联性随着地形变化而变化。当地形起伏越大,地貌越复杂时,多波束测深ping与ping之间的关联性越弱;当地形越平坦,地貌越简单时,多波束测深ping与ping之间的关联性越强;当ping数超过一定值时,ping与ping之间的关联性将消失,部分异常值也将被淹没在真实地形所对应的连续高密度集群中。因而不能使用同一ping数规模值划分整个测区的聚类区块,根据人工交互处理经验,对于地形平坦数据质量好的区域,使用30 ping以上的规模依然可以正常识别异常值,但不建议超过100 ping;对于地形复杂数据质量较差的区域,一般不超过30 ping,通常在20 ping以内可以正常识别异常值,对于极其复杂的地形通常需要在10 ping以内识别。
在多波束测深系统中,中央波束所获取的水深值可信度最高,中央波束所测得水深能够较好地代表该ping所测区域水深,而相邻多ping中央波束水深值的最大差值dlt_depth_max则能够反映该区域地形起伏剧烈程度。本文算法以相邻多ping中央波束水深值最大差值来约束ping数规模的大小。当设定一定阈值后,地形越平坦,区域参与聚类的ping数规模就越大;地形越起伏,区域参与聚类的ping数规模就越小,ping数规规模因而能够随着地形起伏剧烈程度而改变。本文选取水深测量深度精度(accuracy)v作为该阈值,当n个ping的中央波束水深最大差值刚好小于accuracyv时,则n即为此次聚类ping数规模的取值。
(2) 窗口大小(window_num)。该参数表示当前聚类区块吸收每ping的波束数,可控制聚类区块垂直于测量船航行方向的检测精度,通常取25~50,默认取值25。
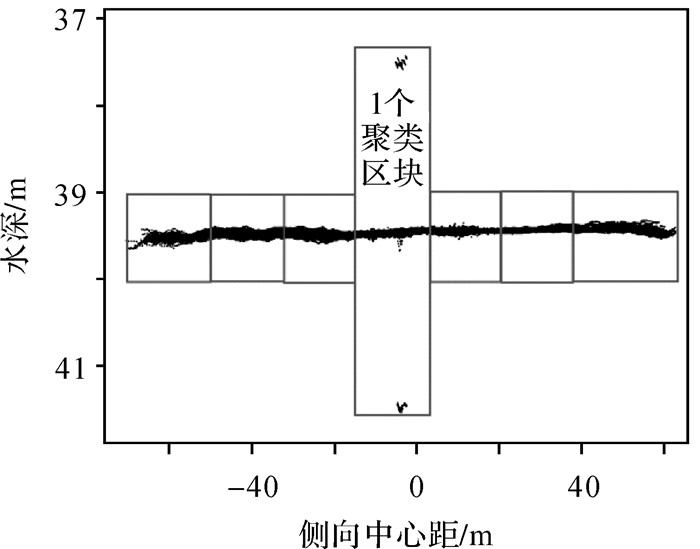
针对某一测区的聚类实施过程,如图 7所示,先通过参数ping_scale从测区数据中获取一个ping切块,然后通过参数window_num从当前ping切块最左边开始窗口滑动获取聚类区块,直至该ping切块所有水深点聚类完毕,进入下一ping切块重复窗口滑动直至所有ping结束。为避免窗口边缘数据被误判,加强相邻两聚类区块数据分类的彼此验证,滑块每次滑动时预留窗口大小的20%与上一聚类区块重叠。
|
| 图 7 聚类区块划分 Fig. 7 Diagram of clustering block division |
3.1.3 各区块聚类参数自适应
明确聚类区块后即可设置该区块内聚类参数,主要参数包括邻域半径(Eps)和邻域内最少点数(MinPts),针对每个聚类区块的密度特征自动选取合适的聚类参数是有效识别异常值的关键。
(1) 邻域半径自适应。邻域半径主要控制核心点的核查范围,在后视图中,y轴为水深值,x轴为侧向中心距,故任意两个水深点之间的欧氏距离由水深值差值和侧向中心距差值决定,以上两个差值在异常值检测过程中可以进一步理解为定位检测精度和深度检测精度,可根据《海道测量规范》[26]所规定的测量精度标准设置(表 1)。然而表中深度精度随水深值变化而变化,为使得邻域半径的取值尽量准确,决定深度精度的水深值应当能够反映当前聚类区块中绝大部分水深数据点的分布深度,为此本文利用中值排序方法确定聚类区块内代表性水深值,并据此得到深度精度值,随后应用式(2)可得当前区块的第1个聚类参数领域半径的取值
 (2)
(2)
| 等级 | 海区举例 | 定位精度(置信度95%) | 深度精度(置信度95%)±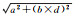 |
| 一级 | 关键航道、锚地 | ±2.0 | a=0.25,b=0.007 5 |
| 二级 | 航道、港口及港口入口 | ±5.0 | a=0.5,b=0.013 |
| 三级 | 一、二级外的沿岸海区或水深小于200 m的区域 | ±20.0 | a=1.0,b=0.023 |
| 四级 | 一、二、三级外的其余海区 | ±100.0 | a=1.0,b=0.023 |
| 注:a、b为精度控制参数;d为水深值。 | |||
式中,Eps为邻域半径;accuracyh为定位精度;accuracyv为深度精度。
(2) 邻域最少点数自适应。在邻域半径确定的前提下,邻域最少点数直接决定了该邻域内点的密度大小。为使算法设定聚类密度大小尽量符合聚类区块内高密度点集群的密度大小,应当选取当前聚类区块内具有代表性的相邻点间距,代表性的相邻点间距依旧通过中值排序方法获取,并根据式(3)获取当前聚类参数最少点数的取值
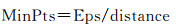 (3)
(3)
式中,MinPts为参数最少点数;Eps为邻域半径;distance为具有代表性的相邻点间距。
3.1.4 聚类实施在聚类实施前先将所有水深点标记为“-1”,表示该点未被任何聚类簇吸收;聚类完毕后,包含点数最多的聚类簇内水深点的标记被更新为“0”,该聚类簇表示可信数据;不能组成聚类簇的水深点被标记为“-1”,表示无效数据。大多数情况下,水深点都将被分为可信数据和无效数据;少数情况下,除核心聚类簇以外,还存在其他规模较小的聚类簇,这些聚类簇被标记为存疑数据,聚类簇内水深点的标记将被更新为“1”。
3.2 人工介入的存疑数据有效性判定现有的各种自动清理算法虽然能够识别出异常值,但却无法进一步准确区分其中的存疑数据,故而清理所得结果中总是包含被误删的异常特征值及误保留的粗差值,这正是导致当前多种自动处理算法可信度较低的关键问题所在。例如,孤立于主要水深点集群的一个规模较小的水深点集群,其产生原因可能是水中悬浮物,也有可能是棱角分明的突起物如石块等,前者代表粗差值应标记为无效数据,后者表示异常特征值应标记为可信数据。针对此类数据目前尚无较好的非人工解决方案,大大限制了现有各种自动清理算法的可信度。存疑数据虽然占比非常少但却至关重要,因为这类数据往往代表地形变化剧烈的特征区域或者非自然地形起伏的目标物,一旦发生误判对整体测量效果影响较大;另外,虽然需要人工介入判别的存疑数据并不多,但通过人工逐ping筛查存疑数据则需要耗费大量时间,因而通过一定算法自动定位存疑数据,并将其交由人工进行有效性判定是提高处理结果可信度与效率的一种可行方案。
存疑数据有效性判定主要考虑以下两方面因素。
(1) 存疑数据形成原因。多波束水深测量存疑数据形成的影响因素有很多,主要分为自身影响因素和环境影响因素,自身影响因素主要包括回波信号丢失或发生错误、换能器旁瓣波束影响、仪器损坏等,环境影响因素主要包括环境中同频工作仪器干扰、水体浑浊或存在大面积悬浮物、海底地势较陡峭复杂(乱石区域)、人为放置的棱角分明的障碍物等。
存疑数据应当首先考虑其产生原因来判定其有效性。明确是由仪器自身原因产生或者外部影响因素干扰原因产生的存疑数据可标记为无效数据,这类原因产生的异常值集群不代表真实海底,应当予以剔除;由于海底地势陡峭复杂或人为放置障碍物等原因造成的存疑数据,应当进一步结合异常值集群的分布特征来判定其有效性。
(2) 存疑数据分布特征。由于真实存在的异常深度而形成的存疑数据,通常都应当呈现出明显的几何形状,即异常值集群有明显的几何特征,如明显的山峰、阶梯或其他规则的几何图形状,这类存疑数据应当标记为有效异常值并予以保留,对于没有明显几何特征的存疑数据,在不影响航行安全的前提下应当标记为无效异常值并予以剔除。
4 试验与分析 4.1 试验数据试验数据源自国产多波束测深系统仪器性能比对项目,数据采集设备为Reason SeaBat T50-P,数据在采集过程中已经进行了安装偏差改正,并在后期进行了声速、潮汐及定位精度改正,试验数据已排除系统误差影响。选取的试验数据位于大连大窑湾海域,平均水深38 m,地形平缓,水质清澈,数据质量较好,为检测各个国产厂家设备对最小目标物的探测能力,试验人员在测区内人工布放一个边长为2 m的立方物。
4.2 试验结果分析布放在测区中的立方物因为边缘棱角分明,与周围水深差值较大,现有自动清理算法往往容易将其视为粗差数据直接剔除,为验证本算法对自动处理算法可信度的增强,本文采取CUBE算法处理结果作为对照,方案1使用CUBE算法进行自动清理,方案2使用本文算法进行清理。
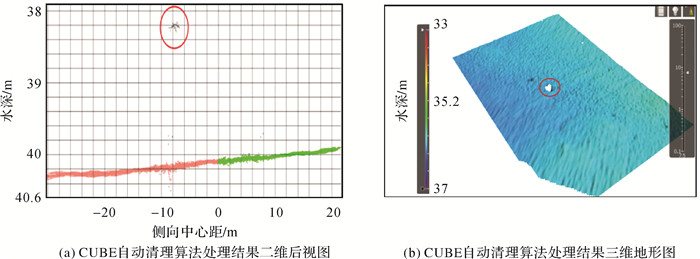
方案1:采用Caris中传统的CUBE算法自动清理异常值,基于Caris软件内自带的CUBE算法选取Shallow模式参数建立CUBE曲面,并以滤波参数2.5进行异常值剔除[27]。处理所得结果如图 8所示。图 8(a)中灰色点代表被CUBE算法滤除的水深数据点,红圈中的灰色点表示为立方物,可以看出这些水深数据被CUBE算法全部当作无效值予以剔除。图 8(b)为处理后所得地形的三维显示效果,可以看出被CUBE算法滤除的数据形成了一个漏洞。
|
| 图 8 CUBE算法处理结果 Fig. 8 The results of CUBE algorithm |
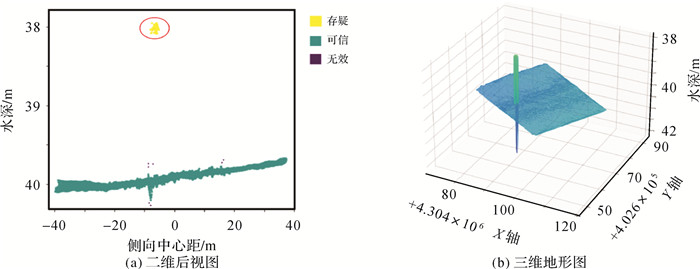
方案2:采用本文算法,处理结果如图 9所示,图 9(a)中绿色聚类簇表示可信数据,紫色散点表示无效数据,红圈内黄色数据点集群表示立方物所产生的水深点集群,表现为孤立于视图内连续高密度区域的点集群,故该聚类簇被准确地标记为存疑数据,有效地区别于被标记为紫色离散数据点所代表的无效数据,存疑数据经识别定位后交由人工介入判定有效性,有效避免了存疑数据被误删影响测量结果可信度的问题,图 9(b)为本文算法处理后所得的地形三维显示,立方物完整地保留下来。
|
| 图 9 本文算法处理结果 Fig. 9 The results of the algorithm in this paper |
试验结果表明,本文算法对数据的分类效果较好,能够准确地集群化异常值与离散异常值的区分,有效避免存疑数据被错误地剔除或保留。
5 结论本文将“存疑数据”概念引入多波束测深异常值的自动清理,为异常值的自动清理提供了一种思路,建立了结合密度聚类算法及部分人工介入的多波束测深异常值清理方法。试验表明,该种自动处理算法有效地将原始水深数据分为可信数据、存疑数据和无效数据3类,保留可信数据、剔除无效数据,并由人工介入判定存疑数据的有效性,一定程度上提高异常值自动清理算法的可信度,具有实际应用价值。但该算法仍旧存在以下不足之处。
(1) 受限于二维视角,该算法仍无法避免部分异常值被遮盖的弊端,这将在一定程度上限制清理结果可信度的提高,下一步将考虑三维聚类算法,以期改善该不足之处。
(2) 由于样本数据标定的困难以及异常值的复杂性,目前尚无法实现存疑数据有效性的自动判定,下一步将引入优化算法实现存疑数据判定的自动化,进一步推进高可信度异常值清理的全自动化。
| [1] |
赵建虎, 刘经南. 多波束测深及图像数据处理[M]. 武汉: 武汉大学出版社, 2008. ZHAO Jianhu, LIU Jingnan. Multi-beam sounding and image data processing[M]. Wuhan: Wuhan University Press, 2008. |
| [2] |
吴自银, 阳凡林, 罗孝文, 等. 高分辨率海底地形地貌探测处理理论与技术[M]. 北京: 科学出版社, 2018. WU Ziyin, YANG Fanlin, LUO Xiaowen, et al. High-resolution submarine topography theory and technology for surveying and post-processing[M]. Beijing: China Science Press, 2018. |
| [3] |
赵建虎, 欧阳永忠, 王爱学. 海底地形测量技术现状及发展趋势[J]. 测绘学报, 2017, 46(10): 1786-1794. ZHAO Jianhu, OUYANG Yongzhong, WANG Aixue. Status and development tendency for seafloor terrain measurement technology[J]. Acta Geodaetica et Cartographic Sinica, 2017, 46(10): 1786-1794. DOI:10.11947/j.AGCS.2017.20170276 |
| [4] |
陆秀平, 黄谟涛, 翟国君, 等. 多波束测深数据处理关键技术研究进展与展望[J]. 海洋测绘, 2016, 36(4): 1-6, 11. LU Xiuping, HUANG Motao, ZHAI Guojun, et al. Development and prospect of key technologies for multibeam echosounding data processing[J]. Hydrographic Surveying and Charting, 2016, 36(4): 1-6, 11. DOI:10.3969/j.issn.1671-3044.2016.04.001 |
| [5] |
LE DEUNF J, DEBESE N, SCHMITT T, et al. A review of data cleaning approaches in a hydrographic framework with a focus on bathymetric multibeam echosounder datasets[J]. Geosciences, 2020, 10(7): 254. DOI:10.3390/geosciences10070254 |
| [6] |
REZVANI M H, SABBAGH A, ARDALAN A A. Robust automatic reduction of multibeam bathymetric data based on M-estimators[J]. Marine Geodesy, 2015, 38(4): 327-344. DOI:10.1080/01490419.2015.1053639 |
| [7] |
BOURILLET J F, EDY C, RAMBERT F, et al. Swath mapping system processing: bathymetry and cartography[J]. Marine Geophysical Researches, 1996, 18(2-4): 487-506. DOI:10.1007/BF00286091 |
| [8] |
CARESS D W, CHAYES D N. Improved processing of Hydrosweep DS multibeam data on the R/V Maurice Ewing[J]. Marine Geophysical Researches, 1996, 18(6): 631-650. DOI:10.1007/BF00313878 |
| [9] |
PEREDA GARCÍA R, PIÑA GARCÍA F, DE LUIS RUIZ J M, et al. Model for the processing and estimation of dual frequency echo sounder observations in detailed bathymetries[J]. Marine Geodesy, 2016, 39(3/4): 305-320. |
| [10] |
LADNER R W, ELMORE P, PERKINS A L, et al. Automated cleaning and uncertainty attribution of archival bathymetry based on a priori knowledge[J]. Marine Geophysical Research, 2017, 38(3): 291-301. DOI:10.1007/s11001-017-9304-9 |
| [11] |
CANEPA G, BERGEM O, PACE N G. A new algorithm for automatic processing of bathymetric data[J]. IEEE Journal of Oceanic Engineering, 2003, 28(1): 62-77. DOI:10.1109/JOE.2002.808204 |
| [12] |
SHAW S, ARNOLD J. Automated error detection in multibeam bathymetry data[C]//Proceedings of 1993 OCEANS. Victoria, BC, Canada: IEEE, 1993: Ⅱ/89-Ⅱ/94.
|
| [13] |
王德刚, 叶银灿. CUBE算法及其在多波束数据处理中的应用[J]. 海洋学研究, 2008, 26(2): 82-88. WANG Degang, YE Yincan. The theory of CUBE algorithm and its application in the processing of multi-beam data[J]. Journal of Marine Sciences, 2008, 26(2): 82-88. |
| [14] |
黄谟涛, 翟国君, 柴洪洲, 等. 检测多波束测深异常数据的CUBE算法模型解析[J]. 海洋测绘, 2011, 31(4): 1-4. HUANG Motao, ZHAI Guojun, CHAI Hongzhou, et al. Analysis on the mathematical models of CUBE algorithm for the detection of abnormal data in multibeam echosounding[J]. Hydrographic Surveying and Charting, 2011, 31(4): 1-4. DOI:10.3969/j.issn.1671-3044.2011.04.001 |
| [15] |
黄贤源, 隋立芬, 翟国君, 等. 利用Bayes估计进行多波束测深异常数据探测[J]. 武汉大学学报(信息科学版), 2010, 35(2): 168-171, 214. HUANG Xianyuan, SUI Lifen, ZHAI Guojun, et al. Outliers detection of multi-beam data based on Bayes estimation[J]. Geomatics and Information Science of Wuhan University, 2010, 35(2): 168-171, 214. |
| [16] |
EEG J. On the identification of spikes in soundings[J]. International Hydrographic Review, 1995, 72(1): 33-41. |
| [17] |
LECOURS V, DOLAN M F J, MICALLEF A, et al. A review of marine geomorphometry, the quantitative study of the seafloor[J]. Hydrology and Earth System Sciences, 2016, 20(8): 3207-3244. DOI:10.5194/hess-20-3207-2016 |
| [18] |
张志衡, 彭认灿, 黄文骞, 等. 考虑自然邻点影响域的多波束测深数据趋势面滤波改进算法[J]. 测绘学报, 2018, 47(1): 35-47. ZHANG Zhiheng, PENG Rencan, HUANG Wenqian, et al. An improved algorithm of tendency surface filtering in multi-beam bathymetric data considering the natural neighboring points influence field[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(1): 35-47. DOI:10.11947/j.AGCS.2018.20160565 |
| [19] |
YANG Fanlin, LI Jiabiao, CHU Fengyou, et al. Automatic detecting outliers in multibeam sonar based on density of points[C]//Proceedings of 2007 OCEANS. Aberdeen, UK: IEEE, 2007: 1-4.
|
| [20] |
陈小龙, 庞永杰, 李晔. 基于动态聚类的单声脉冲多波束测深数据滤波[J]. 热带海洋学报, 2013, 32(5): 73-78. CHEN Xiaolong, PANG Yongjie, LI Ye. Single ping filtering of multi-beam echo sounder data based on dynamic clustering[J]. Journal of Tropical Oceanography, 2013, 32(5): 73-78. |
| [21] |
DAVIES L, GATHER U. The identification of multiple outliers[J]. Journal of the American Statistical Association, 1993, 88(423): 782-792. DOI:10.1080/01621459.1993.10476339 |
| [22] |
DEBESE N, MOITIÉ R, SEUBE N. Multibeam echosounder data cleaning through a hierarchic adaptive and robust local surfacing[J]. Computers & Geosciences, 2012, 46: 330-339. |
| [23] |
WANG Shengping, ZHOU Ping, WU Ziyin, et al. Detection and elimination of bathymetric outliers in multibeam echosounder system based on robust multi-quadric method and median parameter model[J]. Journal of Engineering Science and Technology Review, 2018, 11(3): 70-78. |
| [24] |
ESTER M, KRIEGEL H P, SANDER J, et al. A density-based algorithm for discovering clusters in large spatial databases with noise[C]//Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining. [S. l. ]: KDD, 1996: 226-231.
|
| [25] |
王光, 林国宇. 改进的自适应参数DBSCAN聚类算法[J]. 计算机工程与应用, 2020, 56(14): 45-51. WANG Guang, LIN Guoyu. Improved adaptive parameter DBSCAN clustering algorithm[J]. Computer Engineering and Applications, 2020, 56(14): 45-51. |
| [26] |
IHO. Standards for hydrographic surveys[M]. 6th ed. Monaco: International Hydrographic Bureau, 2020.
|
| [27] |
ZHAO Dineng, WU Ziyin, ZHOU Jieqiong, et al. Parameter group optimization by combining CUBE with surface filtering and its application[J]. Journal of Geodesy and Geoinformation Science, 2020, 3(2): 81-92. |



