2. 武汉大学测绘学院, 湖北 武汉 430079;
3. 国家基础地理信息中心, 北京 100830
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
3. National Geomatics Center of China, Beijing 100830, China
随着GPS气象学概念的提出[1],学者们一直致力于开发和改进基于GNSS反演大气可降水量的方法,这使得GNSS成为一种高效、可靠的水汽遥感技术,它具有全天时、全天候、连续运行、低成本、高分辨率及高精度等优点[2-5]。在获取大气可降水量PWV时,需要将天顶湿延迟乘以转换因子,它是加权平均温度Tm的一个函数[6]。因此,准确计算Tm是GNSS获取高精度大气可降水量的关键。Tm是测站上空的温度和湿度廓线沿着天顶方向的数值积分,可以通过无线电探空、大气再分析资料精确计算。然而,全球探空测站分布稀疏,空间分辨率难以满足GNSS气象学需求;大气再分析资料的时间分辨率较低且通常每月更新一次;难以满足实时/近实时Tm计算的要求[7-8]。
文献[1]收集了位于27°N~65°N之间的13个美国探空测站数据并对8718个探空剖面进行分析,发现Tm与地表温度Ts存在很好的线性关系,建立了Bevis公式,成为当前使用最为广泛的Tm线性回归模型。虽然Ts的地理和季节变化可以反映出Tm的地理和季节变化,但基于北美探空数据建立的Bevis公式往往存在区域性的精度差异。因此,学者们进行了大量研究来建立Tm和Ts的区域线性回归模型[9-14]。此外,只须测站位置和时间信息的经验模型逐渐成为Tm计算的主要方法。文献[15]利用2005—2009年全球135个探空测站数据,基于全球气压和温度(GPT)模型构建了GWMT模型,并通过优化建模方法和改善建模源数据提出了一系列改善模型,如GTm-Ⅱ、GTm-Ⅲ、GWMT-Ⅳ、GTM-X及GWMT-D[16-20]。文献[21]考虑了纬度和海拔变化,利用滑动窗口算法建立了GGTm模型。文献[22]提出了考虑线性趋势、年变化、半年变化及空间变化的GTrop模型。此外,经验对流层模型GPT3和UNB3m同样可以提供Tm估值[23-24]。由于开源、易操作、网格分辨率及精度高且可以提供其他对流层参数,GPT3模型成为当前使用最为广泛的Tm经验模型。
研究表明Tm经验模型精度往往低于Tm回归模型[25-27]。为了提高经验模型估计Tm的精度,本文提出一种Tm经验模型的精化方法,它引入地面气温数据并通过最小二乘方法快速获取精化系数,达到对Tm的误差补偿作用。相较基于机器学习等精化方法,本文方法计算公式简便,可以快速推广至任意Tm经验模型,达到模型精化的目的,对改善GNSS水汽反演精度有重要的现实意义。
1 Tm计算原理及模型建立加权平均温度Tm是由测站上空的水汽压和气温在天顶方向的数值积分计算得到的,文献[28—29]给出了Tm的定义及精确计算Tm的方法
 (1)
(1)
式中,T是大气温度,单位为K;e是水汽压,单位为hPa;z为测站上空的垂直高度,单位为m。在常规的探空数据资料中,上述气象参数及高程信息均不是连续值,往往以高度分层的形式存储。因此,式(1)的离散化形式常用于Tm的精确计算
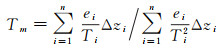 (2)
(2)
式中,下标i代表第i层的气象参数信息。
Bevis模型是基于美国13个无线电探空站2 a的观测资料,共8712条探空廓线建立起来的Tm与Ts线性回归模型
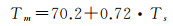 (3)
(3)
基于10 a的ECMWF再分析资料的37个气压层月平均数据,文献[23]提出了GPT3模型。作为GPT系列模型的最新版本,GPT3模型可以提供全球范围内1°×1°格网点上加权平均温度的平均值、年周期和半年周期变化。依据测站位置和时间信息,可以利用式(4)快速获取其Tm估值
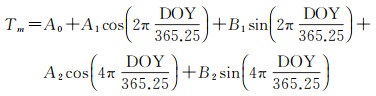 (4)
(4)
式中,A0表示模型格网点Tm的平均值;A1和B1表示模型格网点Tm的年振幅;A2和B2表示其半年振幅。
由于GPT3模型的建模源是月平均数据,其模型只包含年和半年周期项,缺乏表示Tm随高程变化的Tm递减率参数,其精度往往受到限制。通过对实测Tm与GPT3估计Tm的差异和实测Ts与GPT3估计Ts的差异进行分析,其线性相关系数达到了0.62,如图 1所示(使用第2节试验中的数据)。因此,本文提出一种GPT3模型估计Tm的精化方法,它将地面气温数据引入并利用最小二乘获取精化系数。具体地,该精化模型如式(5)所示
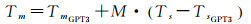 (5)
(5)
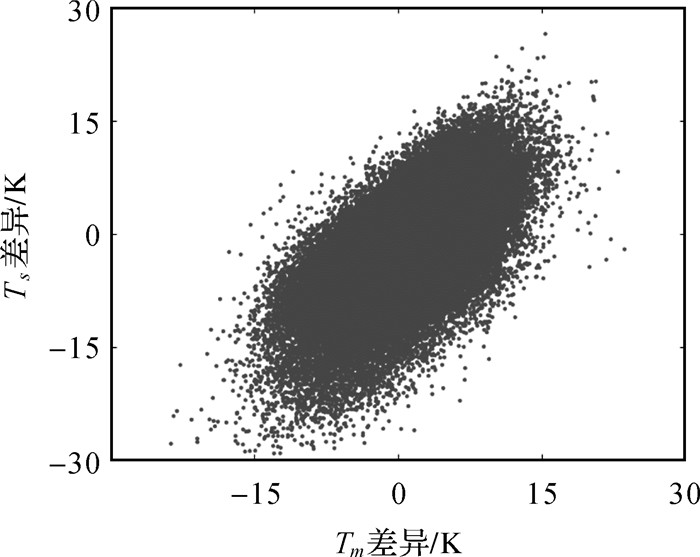
|
| 图 1 Tm差异与Ts差异示意图(实测值与GPT3估值) Fig. 1 The diagram of Tm differences and Ts differences (measured values and GPT3 estimates) |
式中,Tm和Ts分别为加权平均温度真值和地表温度真值;TmGPT3和TsGPT3分别表示由GPT3模型估计得到的加权平均温度和地表温度;M表示实测地表温度和模型估计地表温度差异的权值,即精化模型的精化系数,可以通过最小二乘拟合得到。
2 试验描述本文选择2011—2015年我国与邻近区域的探空站点资料,以及对应的地面气象资料进行GPT3模型区域精化。探空数据分辨率为12 h,即每天固定在UTC 0:00和UTC 12:00。探空剖面包括了不同高度的气压、温度等气象信息。为了计算准确的Tm,需对探空剖面信息进行严格的质量控制,只有满足以下条件的剖面数据才可以用式(2)计算Tm[26]:①探空数据中最后一个有效记录的高度不低于10 km;②探空数据中有效的观测值数量不少于20个;③两个连续高度层之间的高差应不超过1 km;④任何两个连续高度层的气压差值不大于200 hPa。
经过质量控制,本文选取我国及邻近区域180个探空测站,其范围为0°N~65°N,60°E~145°E,如图 2所示。图 2(a)表示用于模型精化的130个探空测站的分布情况。通过GPT3模型,利用双线性内插算法并考虑测站与模型格网点高程差异,可以获取这些测站的Tm和Ts估值[23]。联合探空测站数据获取的精确加权平均温度和地表温度,便可利用式(5)拟合得到本文中模型精化系数M=0.47,构建基于GPT3的精化模型。图 2(b)表示用于模型精度检验的50个探空测站分布。
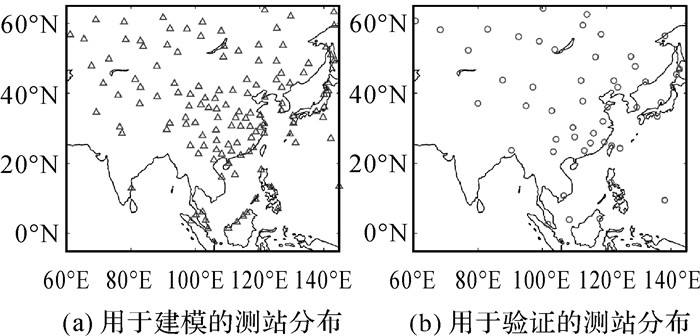
|
| 图 2 研究区域及测站分布 Fig. 2 The map of the research area and the distribution of the sites |
为了验证所提精化模型的优势,本文还利用上述130个探空测站的地面气温和加权平均温度信息,基于Beivs模型的思路,构建了上述研究区域的Tm-Ts线性模型。区域线性模型表达为Tm=53.45+0.78·Ts。因此,本文比较了4种模型在我国及邻近区域估计Tm的精度。它们分别为Bevis模型、区域线性模型、GPT3模型和基于GPT3的精化模型。本文选取3个统计量,即均方根误差(RMSE)、平均绝对误差(MAE)及相关系数(R)作为标准来比较和评价4种模型估计Tm的精度。
3 精度比较与分析利用上述4种模型,分别计算50个验证测站2011—2015年不同时刻的Tm,共141 110个数据。将探空剖面信息计算的相应时刻Tm作为参考值,绘制了散点图,如图 3所示。图中虚线表示1∶1的直线,直线表示模型Tm估值与Tm真值的线性拟合直线。可以发现,基于GPT3的精化模型表现优于其他3种模型,其点分布在拟合线附近的密度高于其他模型,且其斜率达到了0.93。相较于Bevis模型,区域线性模型的点位分布密度没有明显差别,但其拟合斜率得到有效改善,说明构建局部区域Tm-Ts线性模型可以提高Tm估计精度。注意到GPT3模型估计的Tm有明显的界限(图中方框位置),即无论真实Tm值变得多小或多大,GPT3估计的Tm值总为243 K或290 K左右。而基于GPT3的精化模型较好地解决了这一问题,使其可以准确估计任何范围的Tm值。
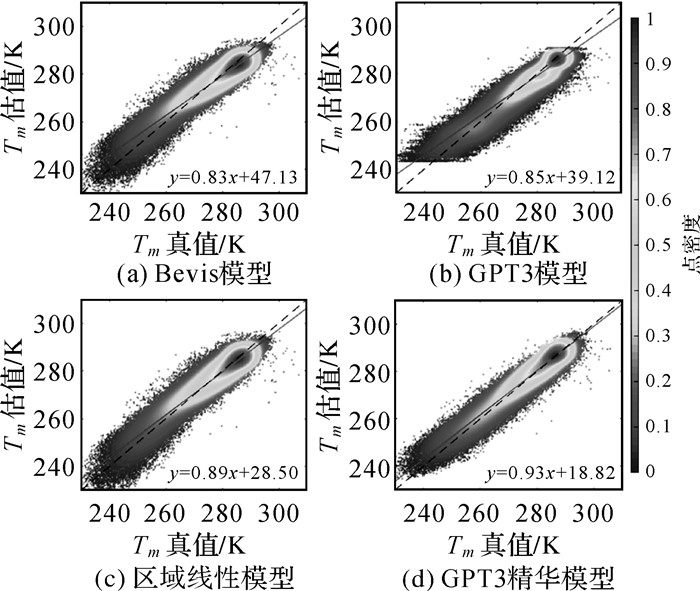
|
| 图 3 4种模型Tm估计值与Tm真值的散点图 Fig. 3 The scatter plots of the estimated Tm against the true Tm with four models |
此外,利用4种模型估计Tm的残差计算了它们各自的MAE和RMSE,不同模型估计Tm与Tm真值的相关系数R也被统计,并列于表 1。GPT3模型表现最差,其MAE、RMSE和R分别为3.43 K、4.46 K和0.94。基于GPT3的精化模型不仅有效改善了GPT3模型的精度,也优于基于Tm-Ts线性关系的区域模型的精度。相较于其他3种模型,基于GPT3的精化模型对MAE和RMSE的改善量分别达到了0.53、0.68、0.38 K和0.68、0.94、0.55 K。
| 模型 | MAE/K | RMSE/K | R |
| Bevis模型 | 3.28 | 4.20 | 0.95 |
| GPT3模型 | 3.43 | 4.46 | 0.94 |
| 区域线性模型 | 3.13 | 4.07 | 0.95 |
| 基于GPT3的精化模型 | 2.75 | 3.52 | 0.97 |
为了分析4种模型在不同区域估计Tm的表现,计算并统计了每种模型在每1个验证测站估计Tm与Tm真值的残差。图 4展示了4种模型估计Tm在各个测站RMSE的空间分布。可以看到,4种模型估计Tm的精度都会受到纬度的影响,即随着纬度的增大精度变差。Bevis模型、GPT3模型和区域线性模型在中高纬度地区估计Tm的精度都较差,甚至出现大量RMSE>6 K的测站。受限于GPT3模型本身在中高纬度较差的表现及Tm在中高纬度区域的变化和波动较大,基于GPT3的精化模型估计Tm的精度也存在纬度上的差异。但是,依然可以看到基于GPT3的精化模型显著改善了其在中高纬度区域估计Tm的精度,其对Tm精度的改善率与其他区域是一致的。另外,基于GPT3的精化模型在其他纬度区域测站的表现同样优于其他3种模型。
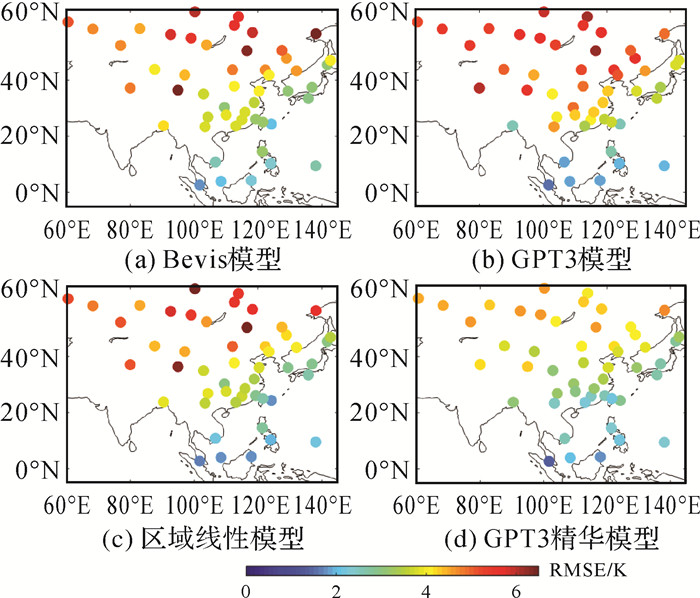
|
| 图 4 4种模型估计Tm的RMSE在不同测站空间分布 Fig. 4 The spatial distribution of RMSE at each site for the four models |
表 2统计了4种模型在不同测站估计Tm的MAE和RMSE,包括最大值、最小值和平均值。可以看到,MAE和RMSE的最大数值都出现在Bevis模型,说明Bevis模型难以服务于全球或大区域的Tm估计,在某些测站会出现较大误差。注意到GPT3模型RMSE和MAE的最大值和最小值都小于Bevis模型和区域线性模型的相应统计量。这表明该测站的Tm变化与建立的整个区域Tm-Ts线性关系不符,需要更加具体、范围更小的区域线性模型。而基于GPT3的精化模型的所有统计量都是4种模型中最小的,其中MAE和RMSE的平均值分别为2.71 K和3.44 K,改善量分别达到了17.1%、20.1%、13.1%和16.7%、20.7%、13.4%。
| 模型 | MAE | RMSE | |||||
| 最大值 | 最小值 | 平均值 | 最大值 | 最小值 | 平均值 | ||
| Bevis模型 | 5.36 | 1.40 | 3.27 | 6.52 | 1.82 | 4.13 | |
| GPT3模型 | 4.82 | 1.19 | 3.39 | 6.26 | 1.60 | 4.34 | |
| 区域线性模型 | 5.21 | 1.29 | 3.12 | 6.45 | 1.66 | 3.97 | |
| 基于GPT3的 精化模型 |
3.73 | 1.09 | 2.71 | 4.75 | 1.33 | 3.44 | |
为了分析4种模型估计不同时刻Tm的精度情况,本文计算并统计了2011—2015年不同模型在每天的RMSE,其时间序列如图 5所示。可以看到,4种模型的RMSE表现出明显的周期性,在冬季总体较大,夏季较小。这是由于Tm本身季节幅度的差异造成,冬季Tm幅度大,往往会使得Tm建模结果变差,导致较大的RMSE。基于GPT3的精化模型得到的RMSE时间序列明显优于其他3种模型,几乎每天都可获得最小的RMSE。进一步,表 3详细给出了不同模型在4个季节估计Tm的RMSE。可以看到,基于GPT3的精化模型在不同季节的RMSE分别为3.83、3.01、3.69、4.06 K,相较于GPT3模型,不同季节的改善量分别达到1.07、0.87、0.85、0.85 K。

|
| 图 5 4种模型在不同时刻的RMSE序列 Fig. 5 The RMSE of the four models at different days |
| 模型 | 春季 | 夏季 | 秋季 | 冬季 |
| Bevis模型 | 4.87 | 3.37 | 4.10 | 4.77 |
| GPT3模型 | 4.90 | 3.89 | 4.54 | 4.91 |
| 区域线性模型 | 4.66 | 3.34 | 3.94 | 4.72 |
| 基于GPT3的精化模型 | 3.83 | 3.02 | 3.69 | 4.06 |
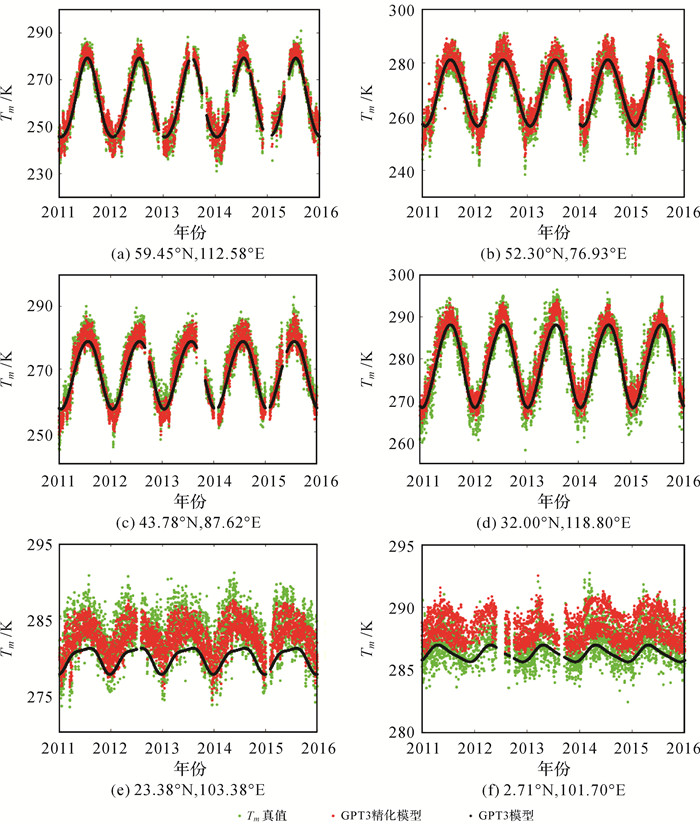
为了更好地理解精化模型对于GPT3模型精度改善的原因,图 6绘制了GPT3模型和基于GPT3的精化模型在不同测站估计Tm的时间序列,且将Tm真值的时间序列作为参考。图 6选取了6个不同区域的测站,这些测站经质量控制后Tm观测值的数量较多。可以看到,在每1个测站,GPT3模型估计的Tm都是一条平滑的周期曲线,只能表现出Tm的季节性变化。而基于GPT3的精化模型在这些测站可以模拟出更复杂的Tm变化,表现出Tm在短时间内的波动和突变,与探空得到的Tm真值具有更好的一致性。
|
| 图 6 模型估计的Tm和探空Tm在不同测站的时间序列 Fig. 6 The Tm time series estimated from the two models and radiosonde observations at different sites |
4 结论
本文提出一种Tm经验模型精化方法,引入地面气温数据并通过最小二乘方法快速获取精化系数,达到对Tm的误差补偿作用。其计算公式简便,可以快速推广至任意Tm经验模型。
基于我国及周边地区180个探空测站,本文开展了区域GPT3模型精化试验和分析。验证结果表明,所提出的基于GPT3的精化模型估计Tm的MAE、RMSE和R分别为2.75 K、3.52 K、0.97,有效改善了GPT3模型的精度,改善量分别为19.9%、21.1%、3.2%;且比基于Tm-Ts关系的Bevis模型和区域线性模型精度要高。此外,空间分布分析表明,基于GPT3的精化模型可以改善传统Tm模型受到纬度的影响,显著提高高纬度区域Tm估计精度;时间序列分析表明基于GPT3的精化模型在不同年积日都可以获得最好的Tm估计,且可以有效解决GPT3模型只能表现Tm季节性变化的缺陷。因此,本文提出的Tm经验模型精化方法可以应用到GPT3模型估计Tm的快速精化中,也可以进一步推广至其他Tm经验模型的精化工作中。
| [1] |
BEVIS M, BUSINGER S, HERRING T A, et al. GPS meteorology: remote sensing of atmospheric water vapor using the global positioning system[J]. Journal of Geophysical Research Atmospheres, 1992, 97(D14): 15787-15801. DOI:10.1029/92JD01517 |
| [2] |
BEVIS M, BUSINGER S, CHISWELL S, et al. GPS meteorology: mapping zenith wet delays onto precipitable water[J]. Journal of Applied Meteorology, 1994, 33(3): 379-386. DOI:10.1175/1520-0450(1994)033<0379:GMMZWD>2.0.CO;2 |
| [3] |
DUAN J P, BEVIS M, FANG P, et al. GPS meteorology: direct estimation of the absolute value of precipitable water[J]. Journal of Applied Meteorology, 1996, 35: 830-838. DOI:10.1175/1520-0450(1996)035<0830:GMDEOT>2.0.CO;2 |
| [4] |
赵庆志, 姚宜斌, 姚顽强. 顾及层析区域外测站的GNSS水汽层析建模方法[J]. 测绘学报, 2021, 50(3): 285-294. ZHAO Qingzhi, YAO Yibin, YAO Wanqiang. A method to establish the tomography model considering the data of GNSS stations outside the research area[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(3): 285-294. DOI:10.11947/j.AGCS.2021.20200111 |
| [5] |
YANG F, GUO J, ZHANG C, et al. A regional zenith tropospheric delay (ZTD) model based on GPT3 and ANN[J]. Remote Sensing, 2021, 13(5): 838. DOI:10.3390/rs13050838 |
| [6] |
ASKNE J, NORDIUS H. Estimation of tropospheric delay for microwaves from surface weather data[J]. Radio Science, 1987, 22: 379-386. DOI:10.1029/RS022i003p00379 |
| [7] |
YANG F, GUO J, MENG X, et al. An improved weighted mean temperature (Tm) model based on GPT2w model with Tm Lapse rate[J]. GPS Solutions, 2020, 24(46): 1-13. |
| [8] |
ZHANG H, YUAN Y, LI W, et al. GPS PPP-derived precipitable water vapor retrieval based on Tm/Ps from multiple sources of meteorological data sets in China[J]. Journal of Geophysical Research Atmosphere, 2017, 122(8): 4165-4183. DOI:10.1002/2016JD026000 |
| [9] |
EMARDSON T R, DERKS H J. On the relation between the wet delay and the integrated precipitable water vapour in the European atmosphere[J]. Meteorological Applications, 2000, 7: 61-68. DOI:10.1017/S1350482700001377 |
| [10] |
LIOU YA, TENG YT, VAN HT, et al. Comparison of precipitable water observations in the near tropics by GPS, microwave radiometer, and radiosondes[J]. Journal of Applied Meteorology, 2001, 40(1): 5-15. DOI:10.1175/1520-0450(2001)040<0005:COPWOI>2.0.CO;2 |
| [11] |
LI J, MAO J. The approach to remote sensing of water vapor based on GPS and linear regression Tm in eastern region of China[J]. Journal of Meteorological Research, 1998, 12(4): 450-458. |
| [12] |
王晓英, 戴仔强, 曹云昌, 等. 中国地区地基GPS加权平均温度Tm统计分析[J]. 武汉大学学报(信息科学版), 2011, 36(4): 412-416. WANG Xiaoying, DAI Ziqiang, CAO Yunchang, et al. Weighted mean temperature Tm statistical analysis in ground-based GPS in China[J]. Geomatics and Information Science of Wuhan University, 2011, 36(4): 412-416. |
| [13] |
WANG S, XU T, NIE W, et al. Establishment of atmospheric weighted mean temperature model in the polar regions[J]. Advances in Space Research, 2019, 65(1): 518-528. |
| [14] |
MAGHRABI A, ALOTHMAN A, ALMUTAIRI M, et al. Variations and modeling of the atmospheric weighted mean temperature for ground-based GNSS applications: central Arabian Peninsula[J]. Advances in Space Research, 2018, 62(9): 2431-2442. DOI:10.1016/j.asr.2018.07.008 |
| [15] |
YAO Y, ZHU S, YUE S. A globally applicable, season-specific model for estimating the weighted mean temperature of the atmosphere[J]. Journal of Geodesy, 2012, 86(12): 1125-1135. DOI:10.1007/s00190-012-0568-1 |
| [16] |
YAO Y, ZHANG B, YUE S, et al. Global empirical model for mapping zenith wet delays onto precipitable water[J]. Journal of Geodesy, 2013, 87: 439-448. DOI:10.1007/s00190-013-0617-4 |
| [17] |
YAO Y, XU C, ZHANG B, et al. GTm-Ⅲ: a new global empirical model for mapping zenith wet delays onto precipitable water vapour[J]. Geophysical Journal International, 2014, 197: 202-212. DOI:10.1093/gji/ggu008 |
| [18] |
HE C, YAO Y, ZHAO D, et al. GWMT global atmospheric weighted mean temperature models: development and refinement[C]//Proceedings of 2013 China Satellite Navigation Conference. Wuhan, China: [s. n. ], 2013.
|
| [19] |
CHEN P, YAO W. GTm_X: a new version global weighted mean temperature model[C] //Proceedings of 2015 China Satellite Navigation Conference. Xi'an, China: [s. n. ], 2015.
|
| [20] |
HE C, WU S, WANG X, et al. A new voxel-based model for the determination of atmospheric weighted mean temperature in GPS atmospheric sounding[J]. Atmospheric Measurement Techniques, 2017, 10(6): 3651-3660. |
| [21] |
HUANG L, JIANG W, LIU L, et al. A new global grid model for the determination of atmospheric weighted mean temperature in GPS precipitable water vapor[J]. Journal of Geodesy, 2019, 93: 159-176. DOI:10.1007/s00190-018-1148-9 |
| [22] |
SUN Z, ZHANG B, YAO Y. A global model for estimating tropospheric delay and weighted mean temperature developed with atmospheric reanalysis data from 1979 to 2017[J]. Remote Sensing, 2019, 11(16): 1893. DOI:10.3390/rs11161893 |
| [23] |
LANDSKRON D, BOHM J. VMF3/GPT3: refined discrete and empirical troposphere mapping functions[J]. Journal of Geodesy, 2018, 92(4): 349-360. DOI:10.1007/s00190-017-1066-2 |
| [24] |
LEANDRO R F, LANGLEY R B, SANTOS M C. UNB3m_pack: a neutral atmosphere delay package for radiometric space techniques[J]. GPS Solutions, 2008, 12: 65-70. DOI:10.1007/s10291-007-0077-5 |
| [25] |
SUN Z, ZHANG B, YAO Y. Improving the estimation of weighted mean temperature in China using machine learning methods[J]. Remote Sensing, 2021, 13(5): 1016. DOI:10.3390/rs13051016 |
| [26] |
LONG F, HU W, DONG Y, et al. Neural network-based models for estimating weighted mean temperature in China and adjacent areas[J]. Atmosphere, 2021, 12(2): 169. DOI:10.3390/atmos12020169 |
| [27] |
DING M. A second generation of the neural network model for predicting weighted mean temperature[J]. GPS Solutions, 2020, 24: 61. DOI:10.1007/s10291-020-0975-3 |
| [28] |
DAVIS J, HERRING T, SHAPIRO I, et al. Geodesy by radio interferometry: effects of atmospheric modeling errors on estimates of baseline length[J]. Radio Science, 1985, 20: 1593-1607. DOI:10.1029/RS020i006p01593 |
| [29] |
YAO Y, SUN Z, XU C. Applicability of Bevis formula at different height levels and global weighted mean temperature model based on near-earth atmospheric temperature[J]. Journal of Geodesy and Geoinformation Science, 2020, 3(1): 1-11. |


