2. 黄河中下游数字地理技术教育部重点实验室(河南大学),河南 开封 475004;
3. 信息工程大学地理空间信息学院,河南 郑州 450001
2. Key Laboratory of Geospatial Technology for the Middle and Lower Yellow River Regions (Henan University), Ministry of Education, Kaifeng 475004, China;
3. College of Surveying and Mapping, Information Engineering University, Zhengzhou 450001, China
面状居民地要素作为地理空间数据的一种,广泛存在于各种大、中比例尺地形图、地籍图中,其主要描述城市和乡镇聚集区中各种建筑物的形状与分布情况。地图上的面状居民地要素通过反映实际居民地的位置、轮廓、基本结构、行政意义以及名称等信息,在城市建模应用中发挥着重要作用[1]。随着我国经济的快速发展,城市化建设进程的加快,城市的面貌日新月异,由此地图更新也越来越频繁,而面状地物的形状分类是地图制图综合和更新的关键技术环节,面状要素的选取、更新、匹配等[2-4]也大多依赖于其形状特征。
形状作为地理要素的一个属性,在地理实体的表达中传递了比颜色、纹理等更多的信息量[5]。在形状描述与分类问题上,国内外学者进行了大量的研究。在描述建筑物形状特征方面,可以大致分为以下几种方式:一是根据地理要素的几何结构特征,基于矢量数据直接定义形状描述子,通过数学模型描述形状的一般特征,进而判断地理要素之间的形状相似性。文献[6—7]使用傅里叶变换度量形状的大小,构建数学模型,定义一系列的几何特征描述形状的相关性,但是该种方法在对不同的形状描述时需要定义不同的相似隶属度函数对每种形状模板进行描述,同时,由于傅里叶变换在形状描述上的不足,该方法对形状的结构比较敏感,对于一些凹凸度较大的要素描述结果较差。文献[8]在描述面状实体时,通过对面状实体的轮廓线定义几何描述算子,设定合理的阈值,进而建立用于面状实体化简的复杂性度量模型。文献[9]运用形态抽象化的方式描述居民地要素的形状,构建居民地形状模板用于居民地的形状识别与化简。二是基于栅格图像数据分析居民地图像的轮廓像素集合描述形状。文献[10]通过构造形状描述链码(chain code)描述建筑物的形状。文献[11]通过小波描述符对图像和形状进行匹配计算。文献[12]使用形状上下文(shape context)来表示形状。文献[13]使用直方图的统计方法计算图像形状信息,以表达图像的形状特征。这些方法的优点是计算思想直观,但却在一定程度上忽略了视觉认知因素。
近年来,随着深度学习技术的发展,深度神经网络在计算机视觉、自然语言处理和语音识别等方面取得了前所未有的成果[14-16]。尤其在机器视觉领域,卷积神经网络(convolution neural network,CNN)对于局部视觉特征具有很强的表现能力,在图像处理、目标检测、图像分割等方面大放异彩[17-19]。部分学者也开始尝试借用图像处理、计算机视觉等领域的技术来解决地理要素的形状识别与分类,其主要思路是将地理矢量数据转为栅格图像,通过卷积神经网络提取图像的轮廓特征,进而描述要素的形状。文献[20—21]将城市中矢量立交桥数据转为栅格图像,通过CNN卷积神经网络和GoogleLeNet神经网络提取道路交叉口的模糊特征,从而判别复杂交叉路口的形状类别。文献[22]利用机器自监督学习的方式,通过卷积神经网络对图像特征学习,结合自动编码机的自监督学习能力对建筑物面要素的几何形状进行度量。
但是,由于矢量数据结构的不规则性,无法将卷积神经网络直接用于矢量数据的处理中。为此,一些研究者提出了基于图的图卷积神经网络(graph convolutional network, GCN)。文献[23]使用图卷积神经网络模型分析建筑物群的分布模式,其主要使用图傅里叶变换和卷积定理,将顶点域卷积转换为谱域中的点积,对建筑物群构成的图进行特征提取,进而给出规则和不规则两种建筑物群的类别判定。文献[24]利用图结构对建筑物的形状进行建模,提出了一种图卷积自编码器(GCAE)模型,提取顶点的局部和区域结构特征,通过无监督学习对建模的图进行分析,实现了形状编码认知。受这些研究启发,本文使用图卷积神经网络中的空间方法来构建端到端的形状分类器,通过对居民地形状信息的多轮次聚合和提取,并将其嵌入一个高维向量中,利用全连接神经网络对高维向量进行分类,以解决在大中比例尺下面状居民地形状分类认知问题。
1 图卷积神经网络 1.1 图上的卷积运算图一般是由节点和边构成,图的定义可以是G=(V, E, A),其中V是节点的集合,E是节点间连接边的集合,A∈Rn×n是图的邻接矩阵,表示节点间边的连接关系和权重[25]。图数据的卷积运算方式分为两种,一种是基于谱方法的卷积运算,另一种是基于空间方法的卷积运算。基于谱方法的图卷积运算借助于信号处理的思想[26],将节点域的输入和卷积核通过傅里叶变换投影到谱域中,在谱域进行卷积运算,然后将得到的结果再逆变换到节点域,以实现图上的卷积运算,这种方式计算复杂度高,占用计算资源大。
本文采用的是基于空间方法的图卷积神经网络模型,该方法的关键思想是基于图上节点状态信息的聚合与更新。文献[27]提出的NN4G(neural network for graphs)是第1个基于空间方法的图卷积神经网络。NN4G通过直接累加节点的邻域信息来实现图的卷积运算。随后,文献[28]提出的扩散卷积网络(diffusion convolutional neural network, DCNN)将图卷积看作是一个扩散过程。它假设信息以一定的转移概率从一个节点转移到相邻的一个节点,使信息分布在几轮后达到均衡。在图结构数据中,每个节点的存在状态并不是相互独立的,节点与节点之间是相互联系与依存的关系。图上卷积运算的空间方法是在节点域直接定义聚合函数[29],在更新中心节点的状态信息时,利用了其相邻节点的状态信息,通过一定的规则将邻居节点的信息,也就是特征,汇聚到中心节点上。通常来说,对于节点间特征的汇聚规则,可以加入一个线性变换矩阵W,作为一种汇聚节点特征的映射关系,即
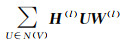 (1)
(1)
式中,U是节点V邻域N(V)中的节点;H(l)是第l层节点的特征。如果加上激活函数,式(1)可以表达为
 (2)
(2)
式中,σ(·)是非线性激活函数;A是图的邻接矩阵,表示节点间的邻接关系;H(l+1)是经第l层汇聚后节点特征的输出。
文献[30]提出了一种用于图中节点分类的图卷积模型,本文借助于其提出的图上卷积运算的方式,将其应用到面状居民地形状分类模型中,其中图上的卷积运算如下
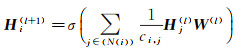 (3)
(3)
式中,N(i)是节点i的相邻节点集合;ci, j是节点的度的平方根的乘积,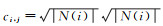
本文借助于节点域中的图卷积神经网络模型,通过叠加多个卷积层构造了面状居民地形状分类模型。该模型是由多个叠加的卷积层和一个线性分类层构成,将面状居民地构造成图数据后提取居民地轮廓几何特征,并将其作为图中节点属性,然后将带有节点属性和标签的图输入到GCN分类模型中,通过多个隐藏层逐层传播,其中从第l层到第l+1层隐藏层的传播计算方式如下
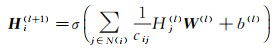 (4)
(4)
式中,N(i)是节点i的相邻节点集合;ci, j是节点的度的平方根的乘积;W(l)是一个特定于层的可训练权重矩阵;b(l)∈R1×D是图卷积网络中的偏置系数;σ(·)表示非线性激活函数,例如ReLU(·)=max(0, ·)。H(l)∈RN×D是第l层的特征矩阵,初始化为H(0)=X,X是图中节点的输入特征,N是图的节点个数,D是每个节点特征向量的维度。
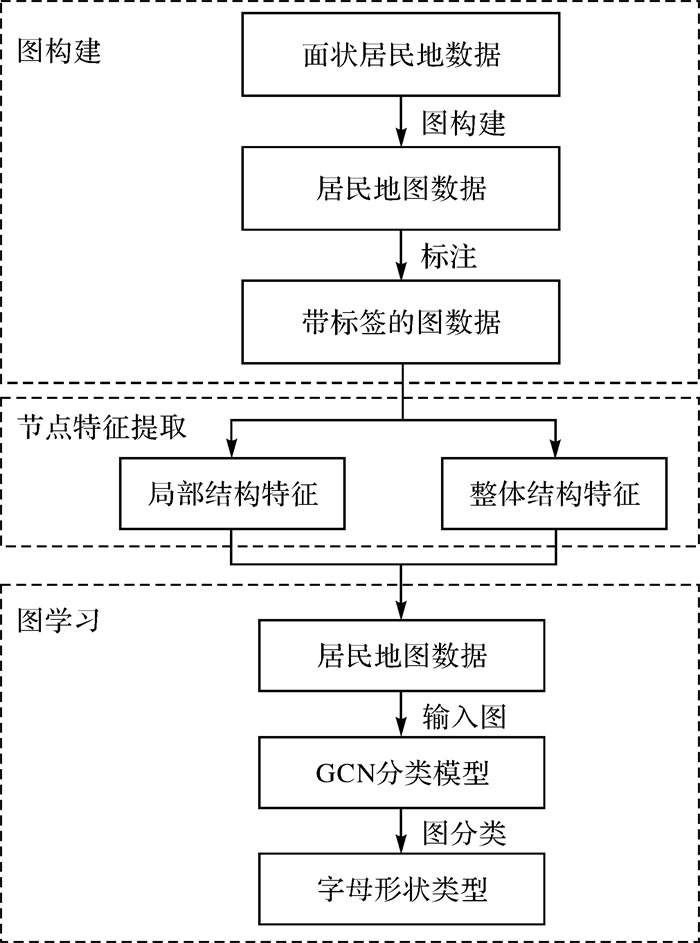
2 基于图卷积神经网络的居民地形状分类模型 2.1 总体思路本文借助于图卷积神经网络对于图数据局部特征敏感的特点,将其运用到地理要素的形状分类与认知中,以图结构表达居民地的形状特征,通过图卷积运算对特征进行学习。本文以面状居民地要素为例,将矢量数据的面状居民地要素建模为图数据结构,依据面状居民地要素的形状类别对相应的图进行标注,通过有监督图学习的方式,运用图卷积神经网络提取面状居民地要素形状的高维结构特征,最后通过分类器对图数据进行分类,以此实现对面状居民地形状的分类。该过程的整体框架结构如图 1所示,主要分为以下几个步骤。
|
| 图 1 基于图卷积神经网络的面状居民地形状分类流程 Fig. 1 Flowchart of areal settlements shape classification based on graph convolutional neural networks |
(1) 图构建:以面状居民地的轮廓多边形描述实体居民地的形状,将多边形线段作为图的节点,以线段之间的连接关系作为边,构建图结构,同时将图按居民地的形状划分成不同的类别进行标注。
(2) 提取节点特征:提取面状居民地轮廓多边形的几何特征,作为节点的属性。
(3) 图学习:以包含节点属性和标注的图作为输入,对多层图卷积神经网络模型进行训练,预测居民地形状的类别。
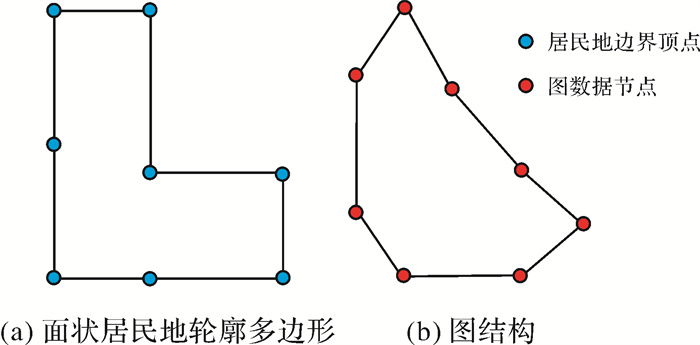
2.2 居民地形状图的构造及标注利用图卷积神经网络进行形状分类的第1步是将面状居民地实体构建为图结构数据,以实现面状居民地矢量形状的图表达。本文采用面状居民地实体的轮廓多边形来描述其形状,如图 2(a)所示,首先提取其轮廓多边形,获取组成面状要素的顶点坐标,将其边界按存储的顶点坐标划分成线段。图神经网络的节点一般代表网络结构中的个体,例如社交网络中的人,软件结构网络中的函数等,边代表了个体之间的关系。具体到居民地形状结构而言,虽然其自然结构可以看作图结构,但居民地的主要信息蕴含在边及其关系上,边界顶点只是表达了边之间的相交与连接关系,基于此考虑,本文以居民地的轮廓多边形线段作为最小形状单元,同时将其作为图数据的节点,线段之间的连接关系作为边,构造成图数据结构,如图 2(b)所示。
|
| 图 2 面状居民地轮廓形状和图结构 Fig. 2 Areal settlement contour shape and its corresponding computation graph |
图的标注是对每个居民地构建成的图数据进行形状类型的标注。根据格式塔原理,人在认知一个物体时,先是从整体上感知物体的全局形状,然后深入到底层分析该物体的局部形状细节。在实际中,对于形状的辨别以人的主观认知为主对形状进行类别的划分,本文采用文献[24]中的人工标注数据。
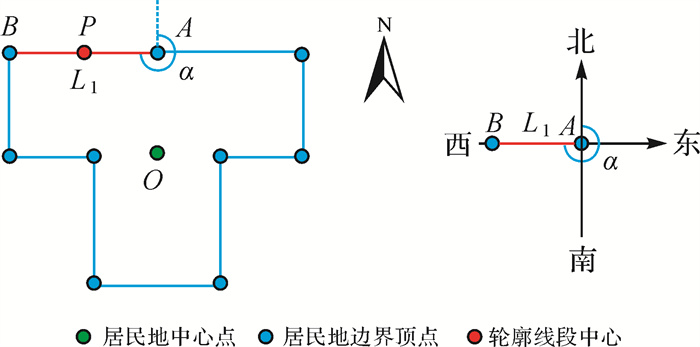
2.3 节点特征的提取 2.3.1 局部结构特征节点的属性特征提取直接影响着整个图的形状表达。在特征提取上,采用面状居民地的轮廓多边形构造图,主要通过描述轮廓多边形线段的几何特征和线段之间的空间关系,实现对面状居民地整体形状的描述。如图 3所示,其中节点P表示面状居民地边界线段AB,提取的特征包含:①边界线段AB的长度L1;②边界线段的方位角α。其中,L1表示由相邻顶点A、B组成的线段长度,方位角α表示线段A、B在二维平面中的方向。本文中以正北方向的北端起,顺时针转至目标直线的夹角,记为该直线的方位角,取值范围是(0, 360°)。
|
| 图 3 节点P的局部特征提取 Fig. 3 Local features extraction of node P |
由于形状特征在平移、旋转和缩放下应该保持不变,故需要对形状特征进行归一化处理。对于边界线段的长度L1,除以面状居民地轮廓多边形的周长D,进行归一化处理;依据方位角α的取值范围,将方位角α除以360°进行归一化处理,具体如下
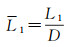 (5)
(5)
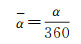 (6)
(6)
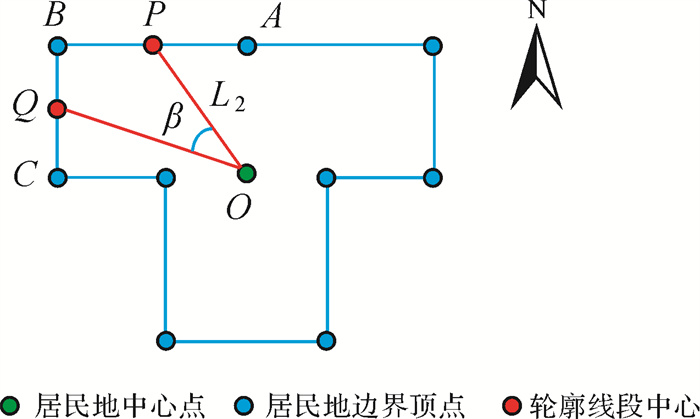
若仅在居民地轮廓多边形上提取边界线段的几何特征,并不能完整地表达居民地的整体形态结构,故本文引入居民地形状中心点,将居民地边界线段的中点与居民地形状中心点相连,从而表达居民地的整体结构特征。如图 4所示,连接居民地中心点与边界线段AB的中点P,提取的特征包含:①线段OP的长度L2;②线段OP到OQ的转向角β。转向角β表示从OP到OQ的角度,逆时针方向为正,否则为负。
|
| 图 4 节点P的整体特征提取 Fig. 4 Global features extraction of node P |
同理,需要对提取的特征进行归一化处理,将居民地中心点O到各线段中点的长度L2累加和记为S,将L2除以S进行归一化;依据转向角β的取值范围(-180°, +180°),故将转向角β除以360°进行归一化,即
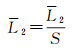 (7)
(7)
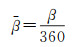 (8)
(8)
在将面状居民地构造成图结构时,需要将面状居民地的轮廓形态也同时映射到图结构中。本文将面状居民地的轮廓形态特征嵌入图的节点中,用图结构表达面状居民地的轮廓形状。图中节点的属性承载着面状居民地轮廓的局部和整体形态特征,由于面状居民地形状的不同,提取到的节点特征也是不同的。因此,在图上进行卷积运算时,可以从不同角度提取形状的特征,在分类预测时,通过全连接神经网络聚合形状特征,并根据获取的形状概率值预测其类别。
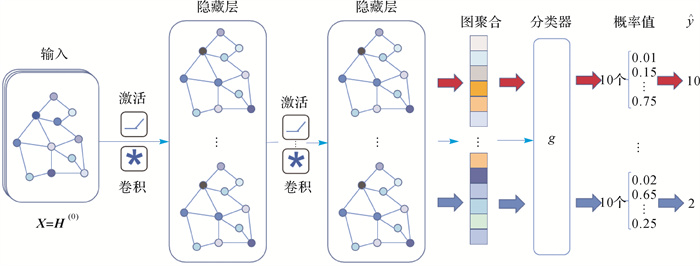
2.4 基于GCN的居民地图分类模型结构基于GCN的居民地图分类模型如图 5所示,模型主要分为两个部分,第1部分是图的嵌入,该过程主要提取图中节点的高维隐藏特征,通过卷积层的运算,将一张图中的节点特征聚合成整张图的图表示,然后将图表示嵌入高维向量中;第2部分是图分类过程,经分类器将得到的高维向量进行形状类别的预测,完成居民地图分类任务。图 5表示输入一个batch的图经过图卷积神经网络将图嵌入高维向量中,每个batch有多个图,每个图得到一个嵌入向量,通过分类器对图的类别进行预测,每个图根据数据集中所划分的类别数得到对应数量的概率预测值,本文试验数据集所划分的类别数为10类,故每个图都有10个概率预测值,表示该图分别属于每一类的概率,选择其中概率值最大的作为其分类标签,图 5分别表示了属于类别10和类别2的两种情况。
|
| 图 5 基于图卷积神经网络的图分类模型 Fig. 5 Graph classification model based on graph convolutional neural networks |
居民地图分类模型的输入数据是带标签的无向图,在该模型的训练中,每次的输入是独立的居民地图数据,输出是预测值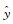
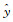
本文采用Python语言和Pytorch深度学习框架实现居民地形状识别的图卷积神经网络模型。所使用的平台为Microsoft Win10 64位操作系统,CPU Intel(R)Core(TM)i7-9700,主频3.0 GHz,内存16 GB,硬盘1024 GB。
建筑物的形状是由设计师和建筑师设计的,而英文字母的形状在建筑物形状中是很常见的,它们可以作为建筑物形状类别的一种简化形式的表达,本文采用文献[32]所述的面状居民地的形状类别划分方法。本文试验所使用的数据来自OpenStreetMap开源数据集,人工选取面状居民地10种类型,包括E形、F形、I形、Y形等,具体形状见表 1,其中,每种类型有500个,数据集样本共5000个,对于英文字母以外的不规则居民地形状,本文暂未涉及。为了使试验结果更加具有客观性,本文试验从10种类型的样本中各随机选取300个,共3000个样本作为训练集,在剩余的2000个样本中随机从每类中选择100个居民地共1000个样本作为验证集,余下的1000个样本作为测试集,训练集、验证集,测试集划分比例为6∶2∶2。
| 形状 | 示例1 | 示例2 | 示例3 | 示例4 | 示例5 | 示例6 | 示例7 |
| E形 |  |
 |
 |
 |
 |
 |
 |
| F形 |  |
 |
 |
 |
 |
 |
 |
| I形 |  |
 |
 |
 |
 |
 |
 |
| Y形 |  |
 |
 |
 |
 |
 |
 |
| Z形 |  |
 |
 |
 |
 |
 |
 |
| O形 |  |
 |
 |
 |
 |
 |
 |
| H形 |  |
 |
 |
 |
 |
 |
 |
| L形 | 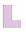 |
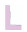 |
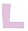 |
 |
 |
 |
 |
| U形 |  |
 |
 |
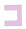 |
 |
 |
 |
| T形 |  |
 |
 |
 |
 |
 |
 |
本文试验中,从OSM获取的数据集为矢量数据,原始数据不能直接作为图数据输入到网络模型中,需要根据原始的矢量数据提取面状居民地的轮廓多边形,以其轮廓多边形线段构造图结构。依据矢量数据在计算机中存储的格式,提取每个面状居民地的顶点坐标,顶点坐标之间用线段连接构成了面状居民地的轮廓多边形。依照2.2节中的方法,利用居民地的顶点坐标构造对应的图。同时,依据居民地的形状对构造的图进行标注,得到带有标签的数据集。对于图中节点的特征提取,依据2.3节中的方法提取对应节点的属性,同时将提取到的属性赋予对应节点,完成图数据的预处理。
3.2 模型结构和参数设置本文试验使用的是一个5层的模型,其包含4个卷积层和1个线性分类层,如图 6所示。通过使用本文所提出的构建居民地图数据及提取节点属性的方法,完成图的构造,然后将构造的带标签的图分批次输入模型,初始化权重参数,并对模型参数进行学习,经反向传播更新权重参数,最大迭代次数为350次,经过试验,选定模型学习率为0.005,训练批次为100。为了防止过拟合,在连续迭代次数为100次且验证集的精确度不再增大时则停止训练。

|
| 图 6 居民地图分类模型参数 Fig. 6 Parameters of areal settlements classification model |
在第1层图输入层中,输入的特征维度是4,嵌入向量维度是128,经过图卷积运算,将第1层输出值传给下一层,激活函数为ReLU函数。
第2至4层的图卷积层作为图卷积神经网络的隐藏层,模型的输入和输出的向量维度是128,激活函数为ReLU函数。
第5层是线性分类层,将隐藏层输出的结果通过分类层进行分类,输出结果为居民地的形状预测类别,分别对应数据集中的形状类别,该层以全连接神经网络和softmax函数作为分类层,全连接层函数如式(9)所示
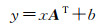 (9)
(9)
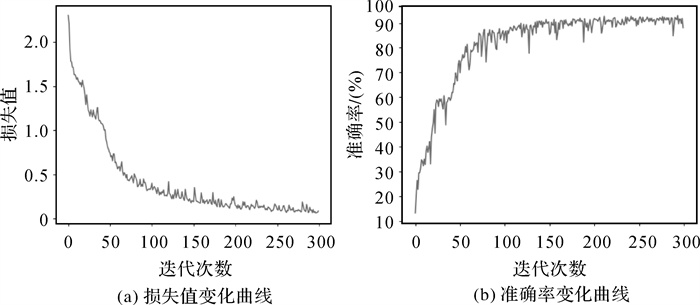
本文试验中训练集和验证集的训练结果如图 7所示,从试验结果可以得出,训练结束后损失值降为0.069,验证集准确度率为92.3%,同时该模型在经过250次的迭代之后,模型能够很好地收敛。从准确率为92.3%可以得出,该模型具有很好的泛化能力,对面状居民地形状的敏感度有很好的效果,能够有效地对面状居民地的形状进行分类。
|
| 图 7 GCN网络模型训练过程中损失值和准确率的变化曲线 Fig. 7 Changing curve of loss and validation accuracy in GCN model training |
3.3 模型参数敏感度分析
在本文试验中,分析了模型的超参数对模型准确率的影响,其中包括训练批次数的大小、节点特征属性的数量、模型的深度(隐藏层层数)和形状嵌入向量维度大小等。
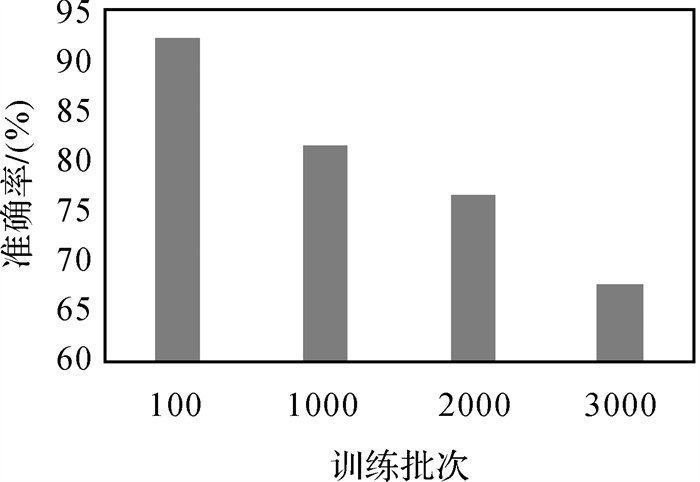
试验中,可以逐个输入训练数据对模型训练,虽然这种每输入一个数据就计算一次损失函数,然后求梯度更新参数的方式训练速度比较快,但是模型训练结果不容易收敛,在梯度下降过程中参数的更新可能在最优点附近来回震荡,始终达不到最优点,两次参数的更新也有可能互相抵消掉,造成目标函数震荡比较剧烈。若遍历全部数据集计算一次损失函数,然后计算函数对各个参数的梯度更新参数,每更新一次参数都需要把数据集里的所有样本遍历一次,计算量大,对于模型的训练传递了较大的误差更新,每次的参数更新过大,因此选择合理的训练批次大小是非常重要的。为了克服这两种方法的缺点,在神经网络的训练中一般采用分批次训练的方式,对此进行了研究与分析,如图 8所示。
|
| 图 8 训练批次数目对模型准确率的影响 Fig. 8 Test of the different number of training batches |
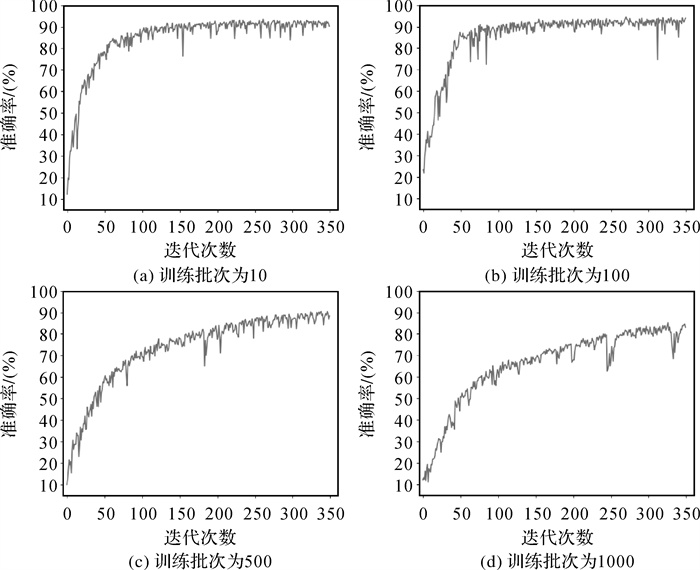
由图 8可以看出,随着训练批次的逐渐增大,模型训练结果的准确率逐渐降低,训练批次的大小对模型的性能产生了较大的影响。在神经网络的训练中,每次梯度的下降是由每一训练批次样本数据总体来决定的。在试验中,对于训练批次小于1000的情况作了进一步研究,改变训练批次的大小,观察模型训练结果的准确率,如图 9所示。由图 9可以看出,在训练批次从10增大到100时,模型训练结果的准确率改变程度并不明显,对模型的性能影响较小;在训练批次从100增大到1000时,模型训练结果的准确率有明显的降低。经过试验,最终选定模型的训练批次为100。
|
| 图 9 不同训练批次模型的损失值 Fig. 9 The loss value of the model at different training batches number |
在模型的层数和形状嵌入向量维度等其他超参数一定时,还分析了使用不同数量的节点属性对模型准确率的影响。对于图结构数据,有两个重要特征影响着图数据:第一是图的空间结构特征,图本身是非欧空间数据,其不规则的空间结构特征对图中节点的邻接关系以及节点间相互作用关系都有很大的影响;第二是图中节点的属性特征,节点的属性特征表示了节点的状态信息。本文在研究过程中,针对节点特征提取的客观性作了探索,使用不同数量的节点特征对模型进行训练,研究模型对于面状居民地形状的敏感度。本文试验中,在设定模型中卷积层层数为4,嵌入向量维度为128时,以及其他条件不变的情况下改变节点的特征数量以研究所提取的居民地特征对于模型性能的影响。
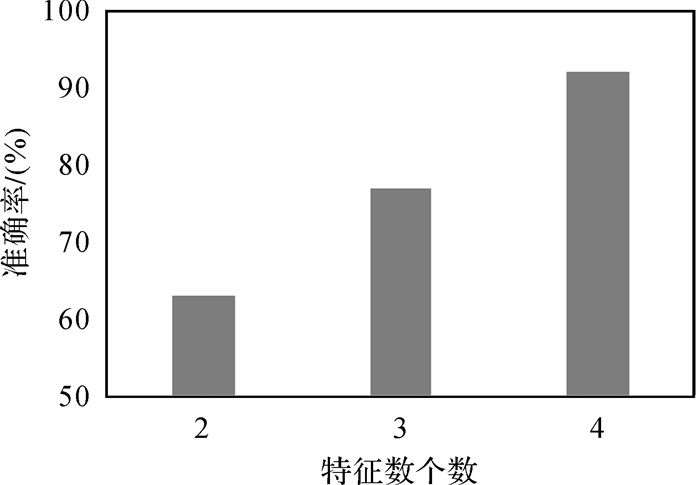
如图 10所示,在节点特征数为2时,即仅以边界线段的长度L1和方位角为特征α时,模型训练后的准确率仅有63%左右。在逐个增加整体结构特征L2和转向角β后,由图 10可以看出,模型训练后的准确率有明显的提高,在由轮廓边界上的特征数量逐渐增加整体结构特征的过程中,可以得出居民地整体形态结构对居民的地形状有着较大的影响,由此可以说明所提取的居民地形状特征的有效性。
|
| 图 10 特征个数对准确率的影响 Fig. 10 Test of the number of vertex attributes |
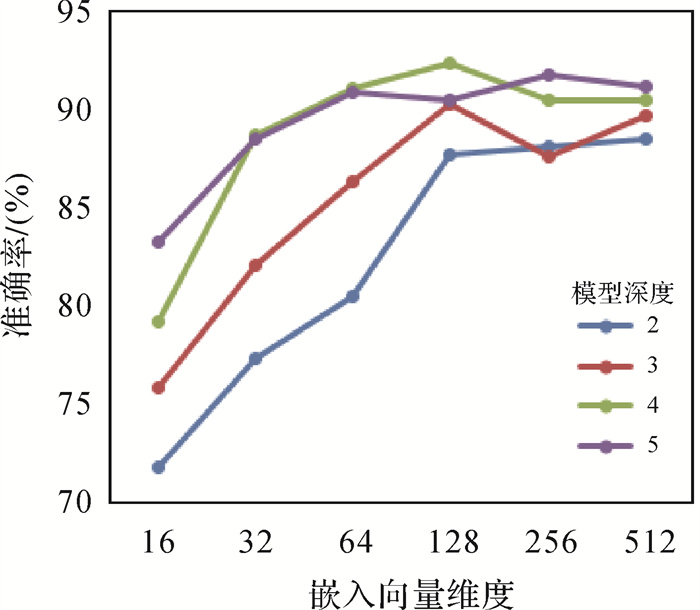
在模型的学习率为0.005、训练批次大小为100等条件一定时,本文试验研究了模型的层数及形状嵌入向量维度对模型性能的影响。由图 11可以看出,在一定条件下,通过增加模型的深度和形状嵌入向量的维度可以提高模型分类的准确率,但这也同样增加了对计算资源的占用和模型训练的时间,并且由于模型采用反向传播来更新权重参数,如果模型复杂度过大会造成梯度消失或梯度爆炸。
|
| 图 11 模型深度和向量维度对模型的影响 Fig. 11 Test of the number of hidden layer and vector dimension |
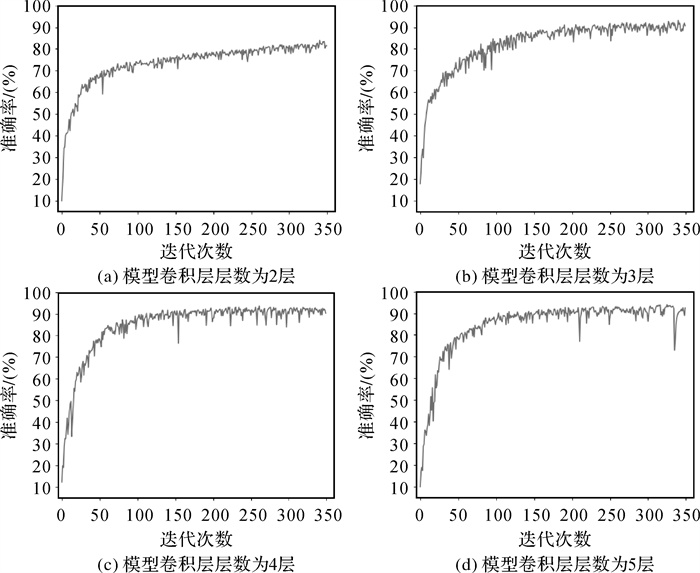
通过试验研究得出使模型最优时的超参数后,进一步研究了模型的深度对模型性能的影响。在模型的其他超参数一定时,如训练批次为100、节点特征数量为4、嵌入向量维度为128、学习率为0.005且最大迭代次数为350次时,研究模型深度对模型性能的影响。如图 12所示,在试验中,以模型分类的准确率作为评价模型性能好坏的指标。图 12中的数据说明,在一定的范围内,增大模型深度,能够提高模型对于形状识别的准确率。
|
| 图 12 模型深度对模型性能的影响 Fig. 12 The results of different hidden layers |
对于该模型来说,当模型层数为4层卷积层,权重维度为128时,模型的性能相对最好,模型分类的准确率为92.3%。同样,在模型深度为5层,权重维度为256时,模型的性能也比较不错,模型准确率为91.7%,但是随着增加模型的深度和权重的维度,模型结构变得更加复杂,易造成过拟合现象,这会削弱模型的泛化能力。
3.4 分类准确率分析为了衡量居民地形状分类模型的好坏,需要给定一个测试集,用模型对测试集中的每一个样本进行预测,并根据模型预测分类的结果计算评价得分。对于分类问题,常见的评价标准有准确率、精确率、召回率和F1值等。本文使用准确率评价模型对所有类别整体分类的好坏,对于每个类的性能估计,使用精确率(P)和召回率(R)进行评估(表 2)。精确率也叫精度或查准率,一个类别的查准率是所有预测为该类的样本中预测正确的比例;召回率也叫查全率,一个类别的查全率是所有真实标签为该类的样本中预测正确的比例。F1值为查准率和召回率的调和均值,表示在两者同样重要时给出的一种指标。
 (10)
(10)
 (11)
(11)
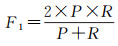 (12)
(12)
| 居民地形状类型 | 人工判别数 | 模型分类数 | 模型分类正确数 | 精确率P/(%) | 召回率R/(%) | F1 /(%) |
| E形 | 100 | 101 | 97 | 96.0 | 97.0 | 96.5 |
| F形 | 100 | 100 | 88 | 88.0 | 88.0 | 88.0 |
| I形 | 100 | 98 | 97 | 98.9 | 97.0 | 98.0 |
| Y形 | 100 | 93 | 89 | 95.7 | 89.0 | 92.2 |
| Z形 | 100 | 101 | 90 | 89.1 | 90.0 | 89.6 |
| O形 | 100 | 99 | 99 | 100.0 | 99.0 | 99.5 |
| H形 | 100 | 93 | 89 | 95.7 | 89.0 | 92.2 |
| L形 | 100 | 103 | 93 | 90.3 | 93.0 | 91.6 |
| U形 | 100 | 104 | 98 | 94.2 | 98.0 | 96.1 |
| T形 | 100 | 108 | 93 | 86.1 | 93.0 | 89.4 |
| 总计 | 1000 | 1000 | 933 | 93.3 | 93.3 | 93.3 |
由表 2可知,该模型对于10种类型的居民地形状有很好的分类效果,模型在精确率和召回率上都有很好的体现,说明该方法在判断居民地形状类别方面有很大的优势。
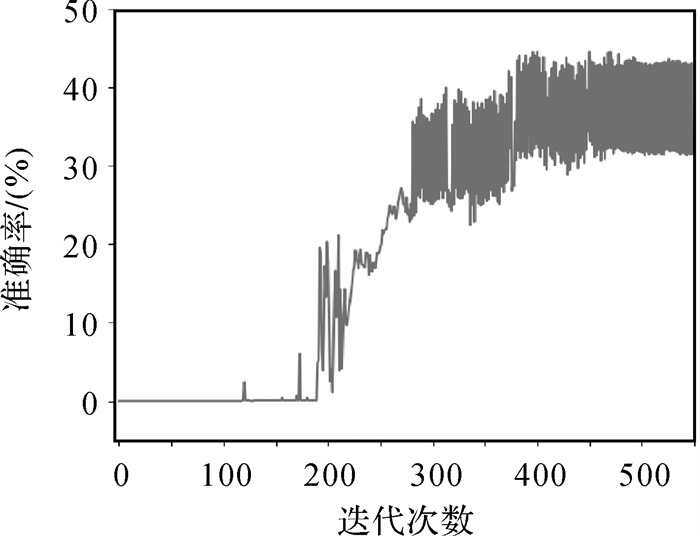
为了对比图卷积神经网络与其他类似方法的差异,本文分别采用多层感知机(multilayer perceptron,MLP)和支持向量机(support vector machine,SVM)进行了对比试验。由于面状居民地轮廓多边形顶点数目的不一致性,在使用MLP和SVM算法时,无法统一输入层的神经元数目,故本文中将面状居民地的轮廓顶点增密到64个,节点的特征提取数量为4,输入的特征维度为256(64×4)。在试验中,MLP算法采用了3层结构,输入为256维的特征向量,隐藏层为128,得到64×10维度的嵌入向量,MLP模型的训练结果如图 13所示。
|
| 图 13 MLP模型训练准确率 Fig. 13 Training accuracy of MLP model |
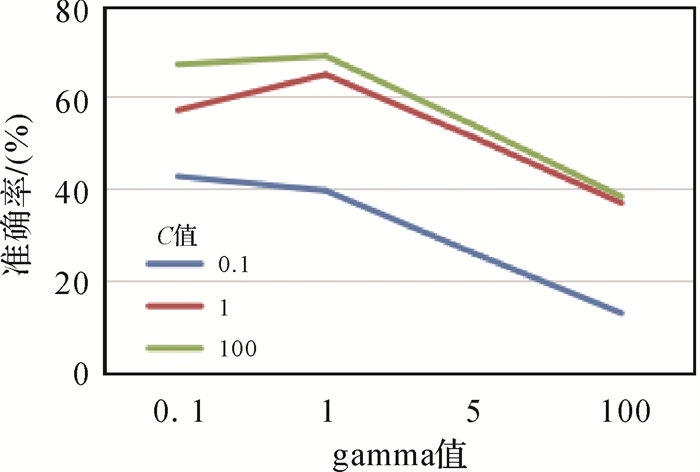
在SVM算法对比测试中,借助于Python中的scikit-learn库实现SVM算法模型,优化机器学习算法的参数值,能有效地提高模型的性能。在SVM算法中,模型性能主要受核函数(kernel)、惩罚系数C以及gamma值的影响。惩罚系数C是对误差的宽容度,C值越大,说明越不能容忍出现误差,容易过拟合;C值过小,容易欠拟合。C值过大或过小,都会使模型的泛化能力变差。gamma是选择RBF函数作为核函数后,该函数自带的一个参数,隐含地决定了数据映射到新的特征空间后的分布。gamma越大,支持向量越少;gamma值越小,支持向量越多,支持向量的个数影响模型训练与预测的速度。在试验中,选择RBF函数作为核函数,经过试验选择了合适的惩罚系数C和gamma值,其中惩罚系数C为100,gamma值为1,具体试验结果如图 14所示。
|
| 图 14 SVM模型训练准确率 Fig. 14 Training accuracy of SVM model |
在对比试验上得到较优结果后,在测试集上进行测试,GCN、MLP和SVM算法的居民地形状分类结果见表 3。
| 指标 | GCN | MLP | SVM |
| 准确率/(%) | 92.3 | 40.3 | 68.3 |
在机器学习领域,MLP和SVM都常用于分类任务中,在居民地形状分类任务中,图卷积神经网络的分类结果是远高于这两种分类方法的。这是因为居民地形状多边形在建模为图结构后能够最大程度地提取、保留居民地的空间几何特征。在图卷积运算的过程中,居民地形状信息在两个层次上进行聚合和传递,一个是顶点内部的属性经过维度扩展(从4维扩展到128维),实现了更高分辨率的属性表达;另一个是顶点间属性聚合及传递,实现了相邻节点形状特征的组合与提取。而多层图卷积神经网络的串行连接,则保证了高阶、远距离形状特征的聚合,故属性信息的维度扩展和多层卷积网络都对最终的分类效果提供了明显的增益效果。此外,GCN在卷积的过程中充分考虑了居民地形状计算图的拓扑结构,通过局域特征的多层次提取来实现图信息的编码表达,而MLP和SVM显然在这些方面难以企及。
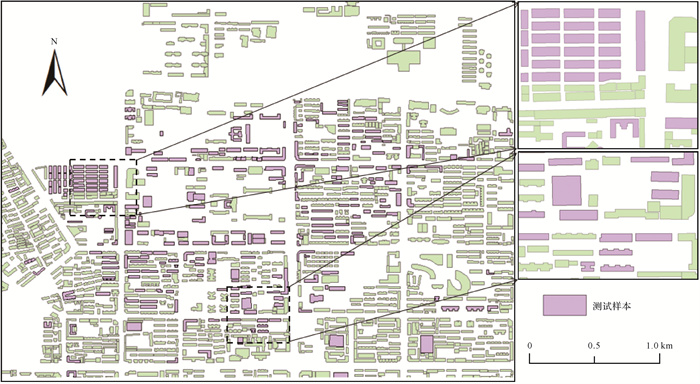
3.5 应用为验证模型的可用性,应用本文中的居民地图形状分类模型对郑州市部分居民地的形状进行识别,试验数据来自OpenStreetMap(OSM)。在郑州市居民地矢量图中,本文选取了部分居民地作为测试对象,如图 15中紫色部分,测试样本数据集中共包含431个样本,人工对选取的居民地进行标注,用训练好的模型对该数据集进行分类,分类结果准确率能达到85.0%左右,精确率为85.1%,召回率为87.7%,模型分类结果见表 4。由图 15可以看出,在实际中建筑物多以矩形为主要,存在类型间数量不均衡的现象。
|
| 图 15 郑州市试验数据 Fig. 15 Experimental data of Zhengzhou |
| 居民地形状类型 | 人工判别数 | 模型分类数 | 模型分类正确数 | 精确率P/(%) | 召回率R/(%) | F1/(%) |
| E形 | 23 | 14 | 12 | 85.7 | 52.2 | 64.9 |
| F形 | 4 | 8 | 2 | 25.0 | 50.0 | 33.3 |
| I形 | 190 | 198 | 185 | 93.4 | 97.4 | 95.4 |
| Y形 | 3 | 4 | 3 | 75.0 | 100.0 | 85.7 |
| Z形 | 19 | 29 | 17 | 58.6 | 89.5 | 70.8 |
| O形 | 58 | 57 | 51 | 89.5 | 88.0 | 88.7 |
| H形 | 28 | 29 | 28 | 96.6 | 100.0 | 98.2 |
| L形 | 41 | 36 | 28 | 77.8 | 68.3 | 72.7 |
| U形 | 37 | 36 | 30 | 83.3 | 81.1 | 82.2 |
| T形 | 28 | 33 | 22 | 66.7 | 78.6 | 72.1 |
| 总计 | 431 | 444 | 378 | 85.1 | 87.7 | 86.4 |
综合前文训练阶段的数据来看,测试集上的模型分类结果要优于试验集,例如测试集的F1主要集中在88.0%~99.5%,见表 2;但是在郑州市试验集上得到的F1分布在33.3%~98.2%之间,见表 4。这主要是因为模型训练和测试所用的数据集与郑州市试验数据集是不同源的两个数据集。在模型训练和测试时,数据集中的10种居民地类型数量相等,数据分布较为均匀;类型内不同居民地间的差异性不大,具体见表 1。在郑州市试验数据集上,选取的是自然居民地数据,该数据主要集中在同一片区域内,数据分布不均匀,见表 2,这造成了10种形状类型的数量各不相同,且类型内居民地形状差异也比较大;试验数据集中F形和Y形的居民地数量明显低于其他类型居民地,过少的样本对试验准确率造成了较大的影响,故在试验数据集上的F1与测试集上的F1差异较大。在下一步的研究中,将会进一步增大训练集和试验数据集,以便更加客观地体现模型分类的准确率。
4 结语面状居民地形状认知与分类对于不同比例尺地形图下居民地的选取、化简及匹配等问题都有重大意义。针对面状居民地典型形状的认知与分类等问题,本文提出一种基于图卷积神经网络的面状居民地形状分类方法。该方法以面状居民地要素的轮廓多边形作为构建计算图的基础,以面状居民地的轮廓多边形线段作为最小单元,提取轮廓多边形线段的几何特征作为计算图的节点属性特征,以图结构表达面状居民地的轮廓形状特征,将带有标签和节点属性的图作为GCN分类模型的输入,通过有监督训练,利用图卷积神经网络对高维形状特征进行分辨,实现面状居民地的形状分类。试验结果表明,依据地理空间中的矢量数据构造计算图,能够有效地利用图结构表达面状居民地的轮廓形状特征,图卷积神经网络能够明显地区分出具有不同属性和结构的图,能够有效地的实现面状矢量数据典型形状的认知和分类任务。
该方法以端到端的模式实现了居民地形状分类的过程,克服了人为设置指标的不足;此外,通过真实数据集的验证,证明该方法能有效地识别出类别内的字母型面状居民地。但本文方法对于类别外的不规则面状居民地形状还无法做出判断,这将是后续要改进的主要工作之一,拟采用聚类和图神经网络相结合的方法深入研究;此外,今后的研究工作还将尝试提高模型的分类准确率,如尝试其他图神经网络类型、增大样本的数据量、更加充分地描述矢量数据的局部以及整体特征等。
| [1] |
STEINIGER S, LANGE T, BURGHARDT D, et al. An approach for the classification of urban building structures based on discriminant analysis techniques[J]. Transactions in GIS, 2008, 12(1): 31-59. DOI:10.1111/j.1467-9671.2008.01085.x |
| [2] |
胡慧明, 钱海忠, 何海威, 等. 采用层次分析法的面状居民地自动选取[J]. 测绘学报, 2016, 45(6): 740-746. HU Huiming, QIAN Haizhong, HE Haiwei, et al. Auto-selection of areal habitation based on analytic hierarchy process[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(6): 740-746. DOI:10.11947/j.AGCS.2016.20150078 |
| [3] |
黄宝群, 盛业华, 郭宁宁, 等. 同名边界点的面状居民地要素匹配[J]. 测绘科学, 2018, 43(2): 108-113. HUANG Baoqun, SHENG Yehua, GUO Ningning, et al. Residential polygon features matching based on identical boundary points[J]. Science of Surveying and Mapping, 2018, 43(2): 108-113. |
| [4] |
张桥平, 李德仁, 龚健雅. 城市地图数据库面实体匹配技术[J]. 遥感学报, 2004, 8(2): 107-112. ZHANG Qiaoping, LI Deren, GONG Jianya. Areal feature matching among urban geographic databases[J]. Journal of Remote Sensing, 2004, 8(2): 107-112. |
| [5] |
LINDSEY D T. Vision science: photons to phenomenology[J]. Optometry and Vision Science, 2000, 77(5): 233-234. DOI:10.1097/00006324-200005000-00008 |
| [6] |
艾廷华, 帅赟, 李精忠. 基于形状相似性识别的空间查询[J]. 测绘学报, 2009, 38(4): 356-362. AI Tinghua, SHUAI Yun, LI Jingzhong. A spatial query based on shape similarity cognition[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 356-362. DOI:10.3321/j.issn:1001-1595.2009.04.012 |
| [7] |
AI Tinghua, CHENG Xiaoqiang, LIU Pengcheng, et al. A shape analysis and template matching of building features by the Fourier transform method[J]. Computers, Environment and Urban Systems, 2013, 41: 219-233. DOI:10.1016/j.compenvurbsys.2013.07.002 |
| [8] |
程绵绵, 孙群, 徐立, 等. 面轮廓线相似性和复杂性度量及在化简中的应用[J]. 测绘学报, 2019, 48(4): 489-501. CHENG Mianmian, SUN Qun, XU Li, et al. Polygon contour similarity and complexity measurement and application in simplification[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(4): 489-501. DOI:10.11947/j.AGCS.2019.20180124 |
| [9] |
晏雄锋, 艾廷华, 杨敏. 居民地要素化简的形状识别与模板匹配方法[J]. 测绘学报, 2016, 45(7): 874-882. YAN Xiongfeng, AI Tinghua, YANG Min. A simplification of residential feature by the shape cognition and template matching method[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(7): 874-882. DOI:10.11947/j.AGCS.2016.20150162 |
| [10] |
YONG K L, ŽALIK B. An efficient chain code with Huffman coding[J]. Pattern Recognition, 2005, 38(4): 553-557. DOI:10.1016/j.patcog.2004.08.017 |
| [11] |
PETER A M, RANGARAJAN A. Maximum likelihood wavelet density estimation with applications to image and shape matching[J]. IEEE Transactions on Image Processing, 2008, 17(4): 458-468. DOI:10.1109/TIP.2008.918038 |
| [12] |
BELONGIE S, MALIK J, PUZICHA J. Shape matching and object recognition using shape contexts[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(4): 509-522. DOI:10.1109/34.993558 |
| [13] |
SAAVEDRA J M. Sketch based image retrieval using a soft computation of the histogram of edge local orientations (S-HELO)[C]//Proceedings of 2014 IEEE International Conference on Image Processing. Paris, France: IEEE, 2014: 2998-3002.
|
| [14] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks[J]. Communications of the ACM, 2017, 60(6): 84-90. DOI:10.1145/3065386 |
| [15] |
KIM Y. Convolutional neural networks for sentence classification[C]//Proceedings of 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP). Stroudsburg, PA, USA: Association for Computational Linguistics, 2014: 1746-1751.
|
| [16] |
ABDEL-HAMID O, MOHAMED A R, JIANG Hui, et al. Convolutional neural networks for speech recognition[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2014, 22(10): 1533-1545. DOI:10.1109/TASLP.2014.2339736 |
| [17] |
SUN Long, WU Tao, SUN Guangcai, et al. Object detection research of SAR image using improved faster region-based convolutional neural network[J]. Journal of Geodesy and Geoinformation Science, 2020, 3(3): 18-28. DOI:10.11947/j.JGGS.2020.0302 |
| [18] |
ZUO Zongcheng, ZHANG Wen, ZHANG Dongying. A remote sensing image semantic segmentation method by combining deformable convolution with conditional random fields[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(6): 718-726. |
| [19] |
GONG Jianya, JI Shunping. Photogrammetry and deep learning[J]. Journal of Geodesy and Geoinformation Science, 2018, 1(1): 1-15. DOI:10.11947/j.JGGS.2018.0101 |
| [20] |
何海威, 钱海忠, 谢丽敏, 等. 立交桥识别的CNN卷积神经网络法[J]. 测绘学报, 2018, 47(3): 385-395. HE Haiwei, QIAN Haizhong, XIE Limin, et al. Interchange recognition method based on CNN[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(3): 385-395. DOI:10.11947/j.AGCS.2018.20170265 |
| [21] |
张鸿刚, 李成名, 武鹏达, 等. GoogLeNet神经网络的复杂交叉路口识别方法[J]. 测绘科学, 2020, 45(10): 190-197. ZHANG Honggang, LI Chengming, WU Pengda, et al. A complex junction recognition method based on GoogleNet model[J]. Science of Surveying and Mapping, 2020, 45(10): 190-197. |
| [22] |
马磊, 闫浩文, 王中辉, 等. 机器自监督学习的建筑物面要素几何形状度量[J]. 测绘科学, 2017, 42(12): 171-177. MA Lei, YAN Haowen, WANG Zhonghui, et al. Geometry shape measurement of building surface elements based on self-supervised machine learning[J]. Science of Surveying and Mapping, 2017, 42(12): 171-177. |
| [23] |
YAN Xiongfeng, AI Tinghua, YANG Min, et al. A graph convolutional neural network for classification of building patterns using spatial vector data[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2019, 150: 259-273. |
| [24] |
YAN Xiongfeng, AI Tinghua, YANG Min, et al. Graph convolutional autoencoder model for the shape coding and cognition of buildings in maps[J]. International Journal of Geographical Information Science, 2021, 35(3): 490-512. |
| [25] |
徐冰冰, 岑科廷, 黄俊杰, 等. 图卷积神经网络综述[J]. 计算机学报, 2020, 43(5): 755-780. XU Bingbing, CEN Keting, HUANG Junjie, et al. A survey on graph convolutional neural network[J]. Chinese Journal of Computers, 2020, 43(5): 755-780. |
| [26] |
SHUMAN D I, NARANG S K, FROSSARD P, et al. The emerging field of signal processing on graphs: extending high-dimensional data analysis to networks and other irregular domains[J]. IEEE Signal Processing Magazine, 2013, 30(3): 83-98. |
| [27] |
MICHELI A. Neural network for graphs: a contextual constructive approach[J]. IEEE Transactions on Neural Networks, 2009, 20(3): 498-511. |
| [28] |
ATWOOD J, TOWSLEY D. Diffusion-Convolutional neural networks[EB/OL]. (2021-12-19). https//arXiv: 1511.02136, 2015.
|
| [29] |
MONTI F, BOSCAINI D, MASCI J, et al. Geometric deep learning on graphs and manifolds using mixture model CNNs[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, HI, USA: IEEE, 2017: 5425-5434.
|
| [30] |
KIPF T N, WELLING M. Semi-supervised classification with graph convolutional networks[EB/OL]. (2021-12-19). https//arxiv. org/abs1609. 02907, 2016.
|
| [31] |
GLOROT X, BENGIO Y. Understanding the difficulty of training deep feed forward neural networks[C]//Proceedings of the 13th International Conference on Artificial Intelligence and Statistics. Sardinia, Italy: [s. n. ], 2010.
|
| [32] |
YAN Xiongfeng, AI Tinghua, ZHANG Xiang. Template matching and simplification method for building features based on shape cognition[J]. ISPRS International Journal of Geo-Information, 2017, 6(8): 250. |



