2. 中国资源卫星应用中心, 北京 100094
2. China Centre for Resources Satellite Data and Application, Beijing 100094, China
分布式合成孔径雷达卫星系统通过编队方式形成多个干涉通道,成员卫星无须物理联系,可提供足够长且灵活可变的基线,并且复图像在同一时刻获得,从而保证了其良好的相关性。近年来,该技术已逐渐发展成为各航天大国的主流研究方向[1-6]。
卫星编队构形设计决定空间基线的长度、指向及其变化情况,而基线矢量又对图像的相关性起着决定性作用,并进而影响干涉相位估计精度,是实现高精度测绘任务重要环节[7-10]。以德国TanDEM-X任务为例,该任务由TerraSAR-X和TanDEM-X两颗卫星组成,是经过在轨验证并成功应用的分布式InSAR卫星系统典型代表,该系统为了获取满足2 m相对高程测量精度要求的DEM产品,从编队卫星的安全性出发先后设计了多组Helix绕飞构形[8-10]。类似地,文献[11]推导了被动稳定编队飞行要素解析解,提出了一种适用于分布式InSAR基线约束的编队构形设计方法。文献[12]分析了串行编队、星下点圆形、空间圆形、干涉车轮和干涉钟摆等典型编队构形相对运动关系特性。文献[13]以满足基线约束的时间比作为优化指标,对编队构形进行优化设计,认为双星空间编队是进行分布式InSAR测高的理想构形。
天绘二号(TH-2)卫星作为我国第1代分布式InSAR卫星系统,由A星和B星两颗卫星组成,并采用一箭双星方式发射入轨形成编队,正常工作模式下双星编队距离小于1 km。该编队系统对于我国乃至全球DEM产品的自主获取具有重要战略意义。与现有设计方法侧重从稳定性与基线对成像性能影响出发开展构形优化不同,在TH-2卫星工程研制过程中发现,卫星编队构形不仅需要被动稳定性好、测绘基线长度满足要求,而且对于构形干涉覆盖区域、电磁兼容安全性,特别是受摄情况下编队卫星被动防碰撞安全性都提出了苛刻要求[14-15]。为此,本文以e/i矢量表示的编队运动学方程理论为基础[16-19],建立构形设计工程约束的数学描述,以构形被动安全性最优为目标,采用启发式算法开展符合多个工程约束条件下的编队构形优化设计。
1 编队相对运动方程为了更好地描述相对轨道运动学的空间几何关系,这里引入e/i矢量描述方法,首先定义如下相对轨道根数Δo矢量[20]
 (1)
(1)
式中,a为轨道半长轴;e为偏心率;i为轨道倾角;Ω为升交点赤经;ω为近地点幅角;u为平纬度幅角;下标1表示主星绝对轨道六根数;下标2表示辅星绝对轨道六根数;Δ表示相对轨道根数之差。同时,式(1)可以进一步做如下定义
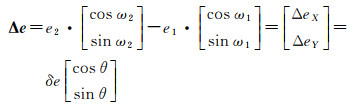 (2)
(2)
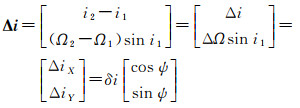 (3)
(3)
式中,δe和θ分别是Δe矢量的大小和相位;δi和ψ分别是Δi矢量的大小和相位。
辅星相对于主星的相对运动可以通过双星编队坐标系下辅星与主星的相对位置Δr=r2-r1来描述,Δr可以表示成
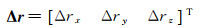 (4)
(4)
在编队坐标系下,相对位置与双星之间相对轨道根数存在对应关系,其转换公式如下
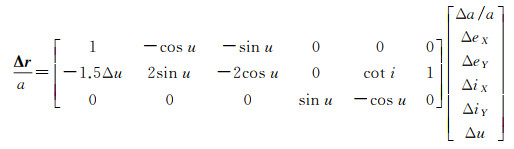 (5)
(5)
考虑到Δa相比于a为小量(稳定构形情况下,Δa近似为0),以分量形式展开可近似得到
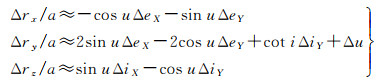 (6)
(6)
令p=aδe,l=a(cotiΔiY+Δu),s=aδi,同时利用三角公式可得
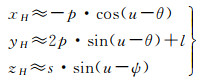 (7)
(7)
式(7)表明编队卫星之间的相对运动可以分解为垂直轨道面的简谐运动与轨道面内的椭圆运动。在编队坐标系下XHOHYH平面内椭圆的相位和大小由Δe矢量决定;l表明主星与椭圆的中心之间的偏移量。
2 编队设计工程约束卫星编队构形是影响天绘二号分布式InSAR系统DEM性能的关键因素。考虑工程实践,首先编队构形需要具备稳定特性,即通过设计实现卫星系统在非球形等保守力摄动下的构形参数发散最小化,这不仅是干涉区域基线稳定的有力保障,而且也是节省构形保持燃料消耗,延长卫星使用寿命的关键因素;其次,要权衡测高精度与去相关效应抑制能力,结合卫星系统波位设计能力通过构形设计来保证系统处于较好的基线长度范围,使得总的测高误差满足期望要求;第三,为了实现卫星系统全球框架下的高精度DEM获取能力,需要设计编队构形以满足全纬度范围的基线约束;最后,为了保障卫星系统在轨5 a寿命期内的编队运行安全,构形设计还要考虑电磁兼容安全性,特别是受空间摄动影响下编队卫星被动防碰撞安全性。
针对上述天绘二号编队构形设计约束,结合双星系统相对运动学特性,建立如下设计约束的数学描述及优化模型。
2.1 构形稳定性约束仅考虑地球非球形引力摄动J2作用下绝对轨道根数长期变化有
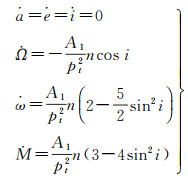 (8)
(8)
式中,pt=a(1-e2);n=a-3/2;J2=1.624×10-3;A1=1.5J2Re2;Re为地球半径。
参考文献[21]的编队构形摄动分析方法,将构形参数p、s、θ、ψ、l对时间求导,并将式(1)—式(3)与式(8)代入化简可得
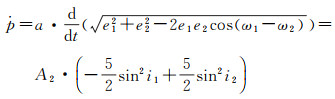 (9)
(9)
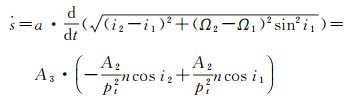 (10)
(10)
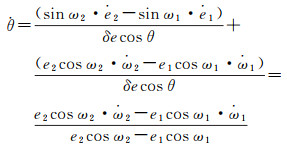 (11)
(11)
 (12)
(12)
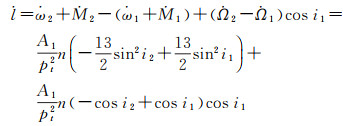 (13)
(13)
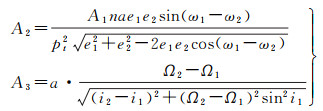 (14)
(14)
若编队卫星轨道倾角相等,即i1=i2,且考虑其运行于近圆轨道,即e12≈e22≈0,则将条件代入式(9)—式(13),可简化得到
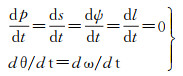 (15)
(15)
由此可知,采用等倾角编队设计原则,相对编队构形每天仅有偏心率矢量的固定旋转,可保证构形J2摄动下的稳定性。
2.2 干涉基线长度约束根据雷达干涉成像原理,当接收天线和目标点不在同一距离向平面内时,成像处理中可经方位向聚焦压缩到距离向平面上,这等同于经典的正侧视情形。根据测量的需要,将空间基线沿航迹和切航迹两个方向上分解为水平基线和垂直基线[22](或视线方向的垂直有效基线)。
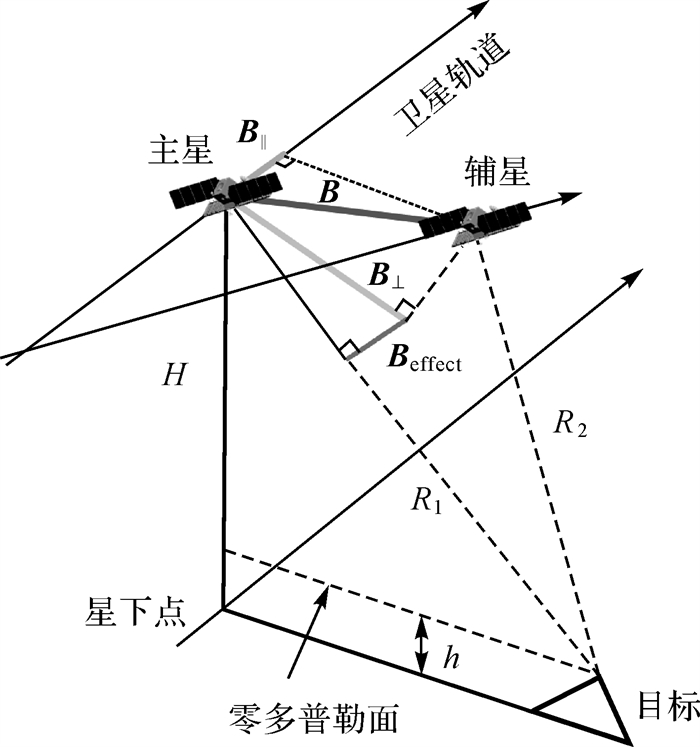
如图 1所示,Hill坐标系中空间基线三轴分量为B=[Bx By Bz]T,则沿航迹基线、切航迹基线和垂直有效基线计算公式为
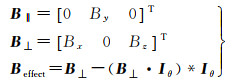 (16)
(16)
|
| 图 1 编队双星基线关系 Fig. 1 Baseline relationship of the formation |
式中,Iθ=[-cosθ 0 -sinθ]T为卫星右侧视情况下雷达到目标视线方向的单位矢量。
根据测量相位差的不确定性与测高误差关系式可知:一方面,要得到最好的测高精度就应当使相位误差、波长和斜距取最小值,即基线长度最大;另一方面,基线越长则去相关效应越严重,当达到临界基线时,两个信号不再相关,有效信噪比为零。因此,存在一个较好的基线长度范围使总的测高误差满足期望要求[23],即
 (17)
(17)
式中,B1为沿航迹基线B‖的上界,通常根据图像相干性要求确定具体数值;B2、B3分别为垂直有效基线Beffect的约束边界,通常需要综合波位设计和地物特征确定。
2.3 干涉覆盖区域约束主星与绕飞星在编队飞行过程中相对位置不断变化,导致卫星间的沿航迹基线和垂直有效基线也随时间和星下点纬度相应变化。若基线长度在可成像的基线长度范围内,则可被成像处理接收;否则,将会给接收信号的图像处理带来困难。故而,编队构形设计需要考虑基线满足前提下的目标覆盖区域能力,其中基线符合性可按式(17)计算判断,基线满足时卫星纬度可利用卫星实时轨道根数,由式(18)计算获得
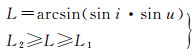 (18)
(18)
式中,L为卫星实时纬度;L1、L2分别为干涉覆盖区域边界,具体根据干涉需求确定。
2.4 电磁兼容安全约束卫星编队在轨运行过程中,通常采取一发双收工作模式[24],即由两颗卫星中的一颗卫星对目标区域发射雷达波束,由编队中的两颗卫星同时接收雷达反射波。为防止另一颗卫星在雷达波照射下不能正常工作,要求编队构形设计过程中能够避免这种情形发生,即星间电磁兼容约束
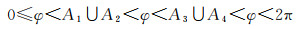 (19)
(19)
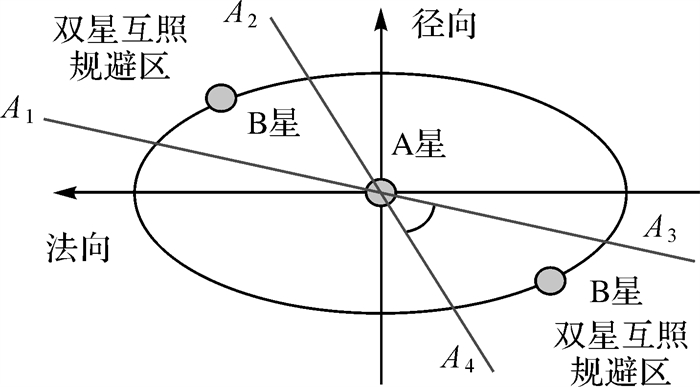
式中,φ为A星与B星质心连线矢量在编队法向平面内投影与法向坐标轴夹角;A1、A2、A3、A4为规避区域边界角度,且满足关系0≤A1≤A2≤A3≤A4≤2π,通常根据载荷波位设计确定。双星编队法向平面坐标系、绕飞规避区及相关角度示意如图 2所示。
|
| 图 2 编队双星互照避免区 Fig. 2 Prohibited range of formation according to the EMC constrains |
2.5 被动防撞安全约束
在空间摄动力(主要为大气阻力)因素影响下,编队构形y向(沿航迹方向)最不稳定,容易发生漂移[25]。因此,为了确保编队构形具有足够的安全性,就需要构形设计结果能够适应y向漂移而不发生碰撞,即被动防撞安全约束条件
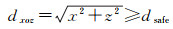 (20)
(20)
式中,dxoz为双星质心距离在编队法向平面内的投影长度;dsafe为安全防碰撞距离,应大于编队双星构型包络,并考虑一定余量。
3 编队构形设计方法工程实际中,考虑到双星编队碰撞风险为在轨运行最大隐患,应优先保障,故而以被动安全距离最大化为构形优化目标。进一步综合上述多个工程化约束分析,可将编队构形设计划归为如下的多约束非线性优化问题
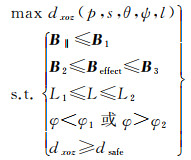 (21)
(21)
为了降低优化问题求解困难,采取理论分析与优化算法相结合的设计思路:首先,从构形在轨受空间扰动力影响,存在构形发散的现象出发,通过建立空间摄动力主部受摄相对运动学方程,并有针对性地开展受摄发散机理研究,给出等倾角的稳定构形设计原则,实现简化设计参数目标;其次,以满足工程设计约束为前提,以编队卫星被动安全性最优为目标函数,利用收敛速度较快的启发式多目标优化算法[26]求解系统综合效能最优构形参数,完成InSAR卫星系统稳定构形设计。
4 试验验证本节将采用本文提出的编队设计方法开展仿真试验,对构形工程约束符合性进行验证,并结合TH-2在轨飞行情况进行方法有效性说明。
轨道初始条件及工程约束样例见表 1。
| 试验内容 | 参数 | 数值 |
| 主星轨道参数 | 半长轴/km | 6906 |
| 偏心率 | 0.001 1 | |
| 轨道倾角/(°) | 97.53 | |
| 升交点赤经/(°) | 100 | |
| 近地点幅角/(°) | 90 | |
| 平近点角/(°) | 90 | |
| 工程设计约束 | 沿航迹基线/m | ≤750 |
| 有效基线/m | 200~600 | |
| 覆盖区域 | 75°S~82°N | |
| 电磁兼容/(°) | 70~90 | |
| 规避区域/(°) | 250~270 | |
| 安全距离/m | 200 |
针对表 1所述的多个工程约束条件,结合第3节所述的方法开展构形优化设计。具体来说,为了降低多约束非线性优化问题的未知数求解纬度,首先进行设计参数简化:考虑到构形稳定性约束要求,通过理论分析确定编队构形等倾角的设计原则,即构形参数中ψ=90°;其次,考虑到编队双星面质比偏差与控制残差会造成星间相对距离漂移,故而不失一般性地采用与TH-2系统类似的双星空间绕飞椭圆构形,主星置于绕飞中心,即构形参数中l=0 m。在此基础上,以安全距离最大化为目标对式(21)描述的优化模型进行求解,确定剩余待求参数。最终的寻优结果见表 2。
| 试验内容 | 参数 | 数值 |
| 辅星轨道 | 半长轴/km | 6906 |
| 偏心率 | 0.001 148 | |
| 轨道倾角/(°) | 97.53 | |
| 升交点赤经/(°) | 100.004 184 | |
| 近地点幅角/(°) | 90.877 2 | |
| 平近点角/(°) | 89.123 4 | |
| 相对构形 | p/m | 355 |
| s/m | 500 | |
| θ/(°) | 110 | |
| ψ/(°) | 90 | |
| l/m | 0 | |
| Δa/m | 0 |
针对表 2中的编队构形寻优结果,进行工程约束符合性验证。
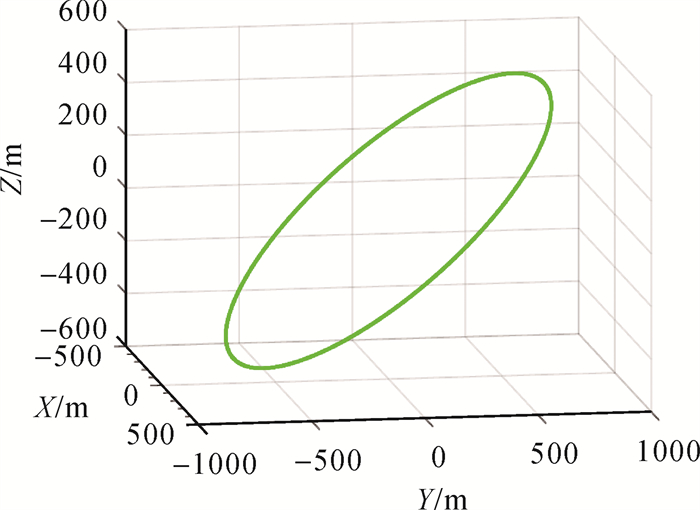
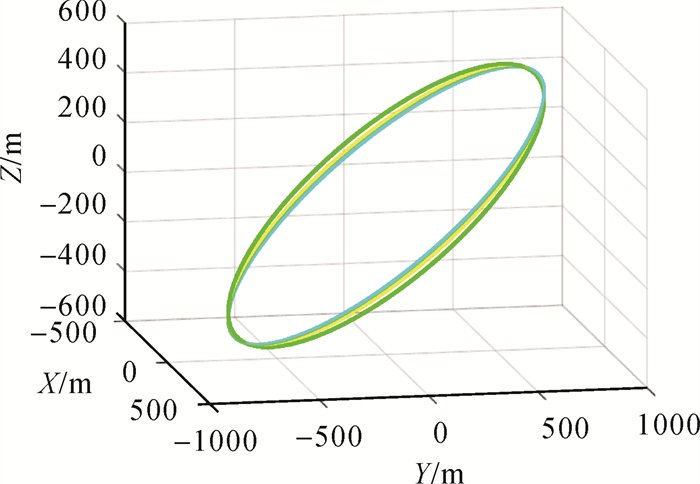
(1) 由编队构形标称轨迹(图 3)与J2受摄一天轨迹(图 4)对比可见,采用本文方法设计的构形大小无改变,仅空间指向发生定量旋转,其原因是偏心率矢量相位角-3.48°/d自然变化导致的,该影响可通过定周期构形保持得以校正,故而编队构形满足稳定性约束。
|
| 图 3 标称编队构形轨迹 Fig. 3 Trajectory of nominal formation configuration |
|
| 图 4 J2摄动一天影响下编队构形轨迹 Fig. 4 Trajectory of formation configuration under J2 perturbaion a day |
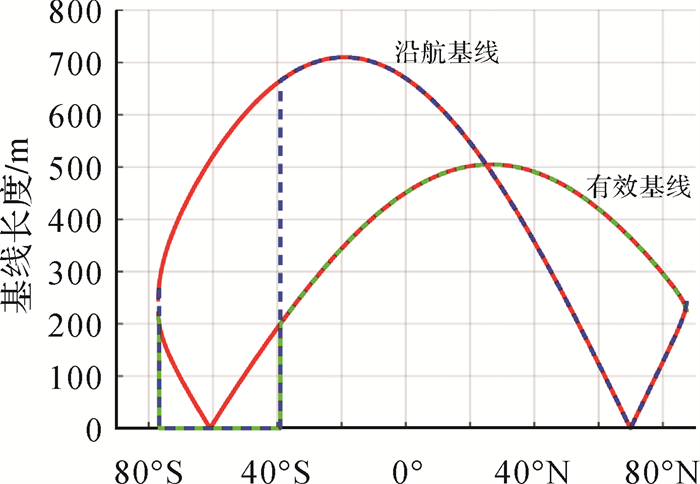
(2) 由升轨(图 5)、降轨(图 6)干涉有效基线与沿航迹基线变化可见,设计构形满足基线约束。

|
| 图 5 基线与可测纬度符合性关系(升轨) Fig. 5 Proof of baseline and coverage in compliance with requirement (ascending pass) |
|
| 图 6 基线与可测纬度符合性关系(降轨) Fig. 6 Proof of baseline and coverage in compliance with requirement (descending pass) |
(3) 由升轨(图 5)、降轨(图 6)基线与可测纬度符合性关系可见,通过升降轨拼接测绘方式,可以实现75°S~82°N纬度带覆盖约束。
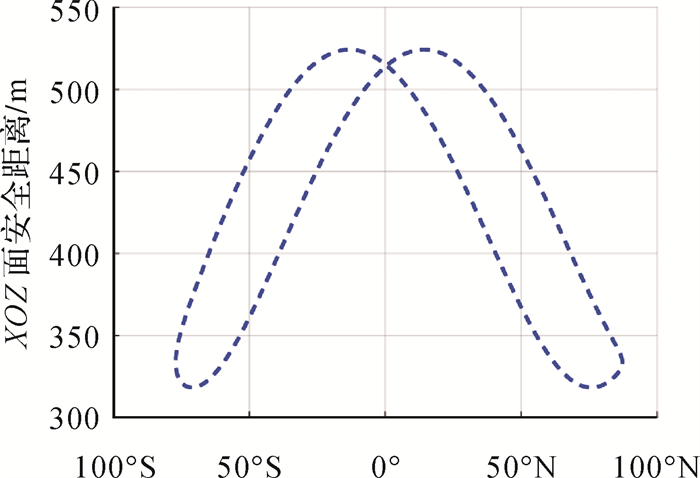
(4) 由编队绕飞相对坐标系XOZ平面(绕飞切轨平面)距离变化情况(图 7)可见,星间安全距离始终大于318 m,满足被动防撞安全约束。
|
| 图 7 空间绕飞安全距离变化情况(XOZ面) Fig. 7 Safe distance variation of the formation (plane XOZ) |
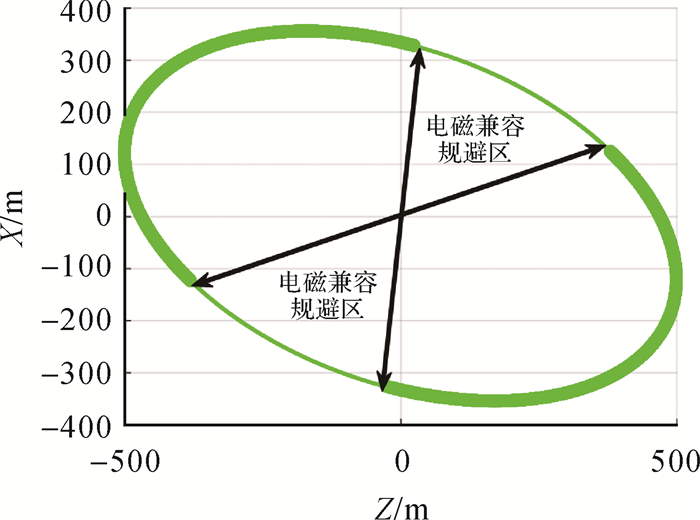
(5) 由空间绕飞电磁兼容规避情况(图 8)可见,编队卫星干涉工作段合理避开电磁兼容规避区域,双星没有互照风险。
|
| 图 8 空间绕飞电磁兼容规避情况 Fig. 8 Avoidance zone according to the EMC constrains |
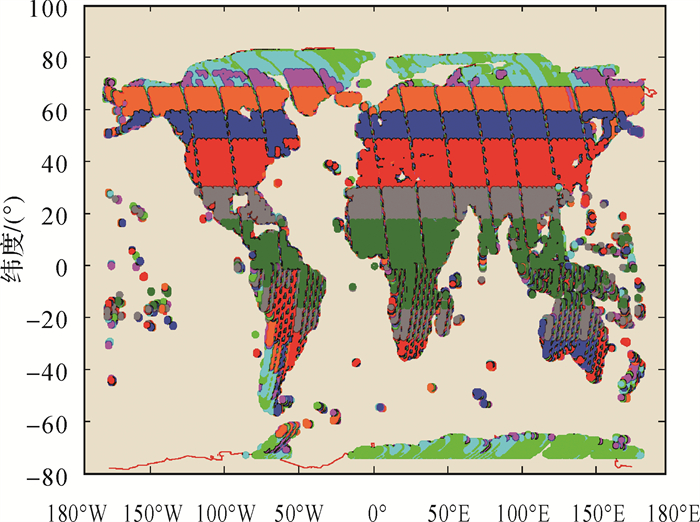
另外,通过在轨状态监视及DEM产品精度校验可知,TH-2卫星系统编队运行3 a以来,构形设计方法有效,运行稳定、安全,目标测绘区域(如图 9所示,其中不同颜色标记了对地干涉采用的不同波位)基线长度满足干涉要求,能够为高质量DEM产品获取提供有力保障。
|
| 图 9 长期区域测绘数据获取情况 Fig. 9 Long term DEM data acquisition |
5 结论
本文针对天绘二号卫星系统需求,提出一种基于多工程约束的分布式InSAR编队构形优化设计方法。该方法首先结合工程实际分析了构形设计约束,并通过引入编队相对运动学模型,实现了设计约束的数学描述;然后针对部分约束条件的理论分析实现求解参数的确定,从而降低未知解空间维度;接下来以构形被动安全性最优为目标,采用蚁群算法对降维的未知参数进行寻优,确定构形参数;最后开展了仿真试验。结果表明,本文方法寻优得到的构形满足设计约束,具备良好的稳定性与被动安全性,并且采用该方法设计的编队构形已经过天绘二号在轨飞行验证,获取的全球框架DEM产品精度高,可以作为后续工程设计的有效参考。
| [1] |
郑浩, 汤晓涛, 陈刚, 等. 一种基于卫星编队InSAR的基线检测方法[J]. 测绘学报, 2010, 39(2): 175-179. ZHENG Hao, TANG Xiaotao, CHEN Gang, et al. InSAR baseline detection based on satellites formation[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(2): 175-179. |
| [2] |
杨元喜, 王建荣, 楼良盛, 等. 航天测绘发展现状与展望[J]. 中国空间科学技术, 2022, 42(3): 1-9. YANG Yuanxi, WANG Jianrong, LOU Liangsheng, et al. Development status and prospect of satellite-based surveying[J]. Chinese Space Science and Technology, 2022, 42(3): 1-9. |
| [3] |
管斌, 孙中苗, 刘晓刚, 等. 双星串飞编队卫星测高模式下高度计相对定标[J]. 测绘学报, 2017, 46(1): 44-52. GUAN Bin, SUN Zhongmiao, LIU Xiaogang, et al. Relative calibration of altimeters under dual-satellite formation flying altimetry mode[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(1): 44-52. DOI:10.11947/j.AGCS.2017.20160050 |
| [4] |
RUNGE H, GILL E. An interformetric SAR satellite mission[C]//Proceedings of the 54th International Astronautical Congress. Bremen, Germany: IEEE, 2003: 1-7.
|
| [5] |
MASSONNET D. Capabilities and limitations of the interferometric cartwheel[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(3): 506-520. DOI:10.1109/36.911109 |
| [6] |
PETERSON E H, FOTOPOULOS G, ZEE R E. A feasibility assessment for low-cost InSAR formation-flying microsatellites[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(8): 2847-2858. DOI:10.1109/TGRS.2009.2017521 |
| [7] |
ALLENDE-ALBA G, MONTENBRUCK O. Robust and precise baseline determination of distributed spacecraft in LEO[J]. Advances in Space Research, 2016, 57(1): 46-63. DOI:10.1016/j.asr.2015.09.034 |
| [8] |
OCHS S, PITZ W. The TerraSAR-X and TanDEM-X satellites[C]//Proceedings of the 3rd International Conference on Recent Advances in Space Technologies. Istanbul, Turkey: IEEE, 2007: 294-298.
|
| [9] |
ZINK M, BARTUSCH M, MILLER D. TanDEM-X mission status[C]//Proceedings of 2011 IEEE International Geoscience and Remote Sensing Symposium. Vancouver, BC, Canada: IEEE, 2011: 2290-2293.
|
| [10] |
KRIEGER G, MOREIRA A, FIEDLER H, et al. TanDEM-X: a satellite formation for high-resolution SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(11): 3317-3341. DOI:10.1109/TGRS.2007.900693 |
| [11] |
陈杰, 周荫清, 李春升. 分布式SAR小卫星编队轨道设计方法研究[J]. 中国科学E辑: 信息科学, 2004, 34(6): 654-662. CHEN Jie, ZHOU Yinqing, LI Chunsheng. Research on orbit design method of distributed SAR small satellite formation[J]. Science in China, SerE, 2004, 34(6): 654-662. |
| [12] |
姜卫平, 赵伟, 赵倩, 等. 新一代探测地球重力场的卫星编队[J]. 测绘学报, 2014, 43(2): 111-117. JIANG Weiping, ZHAO Wei, ZHAO Qian, et al. Satellite formation for a new gravity field exploration mission[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(2): 111-117. DOI:10.13485/j.cnki.11-2089.2014.0016 |
| [13] |
郝继刚, 张育林. SAR干涉测高分布式小卫星编队构形优化设计[J]. 宇航学报, 2006, 27(4): 654-658, 669. HAO Jigang, ZHANG Yulin. Formation optimized design for the height measurement of InSAR using distributed micro-satellites[J]. Journal of Astronautics, 2006, 27(4): 654-658, 669. |
| [14] |
CURLANDER J C, MCDONOUGH R N. Synthetic aperture radar: systems and signal processing[M]. New York: Wiley, 1991.
|
| [15] |
楼良盛, 刘志铭, 张昊, 等. 天绘二号卫星工程设计与实现[J]. 测绘学报, 2020, 49(10): 1252-1264. LOU Liangsheng, LIU Zhiming, ZHANG Hao, et al. TH-2 satellite engineering design and implementation[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(10): 1252-1264. DOI:10.1947/j.AGCS.2020.20200175 |
| [16] |
孙俊, 黄静, 张宪亮, 等. 地球轨道航天器编队飞行动力学与控制研究综述[J]. 力学与实践, 2019, 41(2): 117-136. SUN Jun, HUANG Jing, ZHANG Xianliang, et al. Dynamics and control of spacecraft formation flying in earth orbit[J]. Mechanics in Engineering, 2019, 41(2): 117-136. |
| [17] |
胡敏, 曾国强, 姚红. 基于相对轨道根数的卫星编队重构控制研究[J]. 装备指挥技术学院学报, 2010, 21(1): 74-77. HU Min, ZENG Guoqiang, YAO Hong. Research on satellite formation reconfiguration control based on relative orbit elements[J]. Journal of the Academy of Equipment Command & Technology, 2010, 21(1): 74-77. |
| [18] |
贺东雷, 曹喜滨, 马骏, 等. 基于相对偏心率/倾角矢量的编队控制方法[J]. 系统工程与电子技术, 2011, 33(4): 833-837. HE Donglei, CAO Xibin, MA Jun, et al. Formation control approach based on relative eccentricity/inclination vector[J]. Systems Engineering and Electronics, 2011, 33(4): 833-837. |
| [19] |
D'AMICO S, MONTENBRUCK O. Proximity operations of formation-flying spacecraft using an eccentricity/inclination vector separation[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(3): 554-563. |
| [20] |
曹喜滨, 贺东雷. J2摄动下编队构形保持脉冲控制方法[J]. 系统仿真学报, 2007, 19(23): 5447-5450. CAO Xibin, HE Donglei. Impulsive control approach for formation keeping under J2 perturbation[J]. Journal of System Simulation, 2007, 19(23): 5447-5450. |
| [21] |
D'AMICO S, ARDAENS J S, LARSSON R. Spaceborne autonomous formation-flying experiment on the Prisma mission[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(3): 834-850. |
| [22] |
楼良盛, 刘志铭, 李崇伟. 卫星编队InSAR基线的确定方法[J]. 遥感信息, 2013, 28(2): 9-11, 23. LOU Liangsheng, LIU Zhiming, LI Chongwei. Technique of determining base-line for InSAR based on formation-flying satellites[J]. Remote Sensing Information, 2013, 28(2): 9-11, 23. |
| [23] |
TANG Xinming, LI Tao, GAO Xiaoming, et al. Research on key technologies of precise InSAR surveying and mapping applications using automatic SAR imaging[J]. Journal of Geodesy and Geoinformation Science, 2019, 2(1): 27-37. |
| [24] |
朱建军, 李志伟, 胡俊. InSAR变形监测方法与研究进展[J]. 测绘学报, 2017, 46(10): 1717-1733. ZHU Jianjun, LI Zhiwei, HU Jun. Research progress and methods of InSAR for deformation monitoring[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1717-1733. DOI:10.11947/j.AGCS.2017.20170350 |
| [25] |
BING XU, LIQUN LIU, ZHIWEI LI, et al. Design bistatic interferometric DEM generation algorithm and its theoretical accuracy analysis for LuTan-1 satellites[J]. Journal of Geodesy and Geoinformation Science, 2022(1): 25-38. |
| [26] |
叶发茂, 孟祥龙, 董萌, 等. 遥感图像蚁群算法和加权图像到类距离检索法[J]. 测绘学报, 2021, 50(5): 612-620. YE Famao, MENG Xianglong, DONG Meng, et al. Remote sensing image retrieval with ant colony optimization and a weighted image-to-class distance[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(5): 612-620. DOI:10.11947/j.AGCS.2021.20200357 |


