2. 上海航天控制技术研究所,上海 200233
2. Shanghai Institute of Spaceflight Control Technology, Shanghai 200233, China
分布式干涉合成孔径雷达卫星系统采用编队方式形成多个干涉通道,由于编队成员无须物理联系,故而可提供足够长且灵活可变基线,并且复图像同一时刻获得,保证了其相关性。近年来,编队技术已逐渐发展成为各航天大国主流研究方向[1-8],目前已有GRACE、TanDEM及PRISMA等多项编队飞行任务在轨运行[9-13]。由于受到轨道摄动影响,编队卫星不可避免地会遇到构形控制问题。
TanDEM任务[9, 12]和PRISMA任务[13]针对自身任务特点采用面内两脉冲控制,通过主动偏置半长轴实现相对纬度幅角漂移控制,该方法属于有偏控制,且不能满足相对半长轴、相对偏心率矢量与相对纬度幅角的联合精确控制需求。文献[14—15]皆提出了径向脉冲与沿航迹向脉冲相结合的多脉冲控制方法,虽然该方法属于无偏控制,但考虑到径向脉冲具有控制效率低、燃料消耗多的不足,同时这种控制策略较为复杂,对推力器安装要求多,燃料消耗非最优,不利于工程实现。
本文针对编队保持精确控制问题,采用相对轨道根数描述方式,在传统脉冲控制方案基础上,结合工程实际补偿了控制过程中相对轨道根数间的耦合影响,优化设计了一种面内、面外独立控制的无偏四脉冲编队保持控制方法,制定了相应的控制策略,并已成功应用于天绘二号卫星在轨任务[16]。
1 编队相对运动方程按照描述编队卫星相对运动方式的不同,卫星编队控制分为基于相对位置速度的编队控制和基于相对轨道根数的编队控制。由于相对轨道根数能够直观描述编队卫星之间的几何关系及相对运动状态,同时便于进行单星绝对轨控与编队控制的一体化设计,因而更具应用前景[17-19]。
为了描述辅星相对于主星的运动,定义如下相对轨道根数Δo矢量[20]
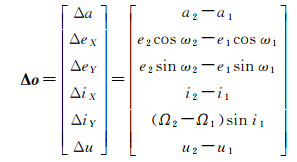 (1)
(1)
式中,下标为1表示主星绝对轨道六根数;下标为2表示辅星绝对轨道六根数。
同时,式(1)可以进一步做如下定义
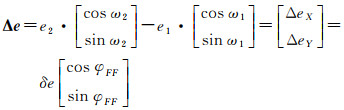 (2)
(2)
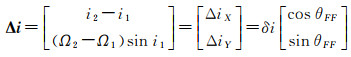 (3)
(3)
式中,δe和φFF分别是Δe的大小和相位;δi和θFF分别是Δi的大小和相位。
同样,r1和r2分别表示主星、辅星在编队坐标系[12]下的位置矢量。辅星相对于主星的相对运动可以通过编队坐标系下辅星与主星的相对位置Δr=r2-r1来描述,则Δr可以表示成
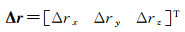 (4)
(4)
在编队坐标系下,相对位置与相对轨道根数之间存在对应关系,其转换公式为[8]
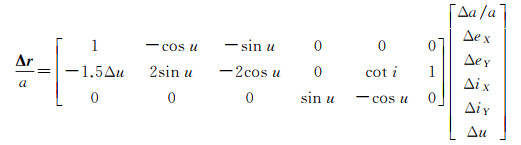 (5)
(5)
式中,考虑到Δa相对a为小量,对式(5)进行近似并以分量形式展开可得
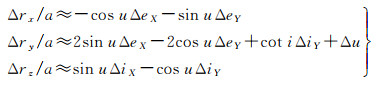 (6)
(6)
令P=aδe,L=a(cot iΔiY+Δu),S=aδi,同时利用三角合角公式可得
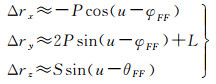 (7)
(7)
式(7)表明编队卫星之间的相对运动可以分解为垂直轨道面的简谐运动和在轨道面内的椭圆运动。P表示辅星相对主星运动轨迹在编队坐标系XOY面内投影椭圆的短半轴;S表示辅星相对主星运动轨迹在编队坐标系Z向上的振幅;L表示主星相对编队构形几何中心在编队坐标系Y向的偏移量。
由上述编队相对位置与轨道根数关系及编队相对运动学方程可知,按照调整轨道根数的不同,编队保持可进一步分解为轨道面内根数(δΔe、δΔa、δΔu)和轨道面外根数(δΔi)的独立控制[21]。
2 编队保持控制算法编队构形是由两颗卫星的相对轨道根数所决定,因此编队构形控制最终变成对编队卫星的相对轨道根数调整。由文献[22—24]的编队构形摄动分析可知,编队构形保持控制主要是调整平面内相对轨道根数与平面外相对轨道根数。
2.1 平面内控制考虑到径向控制效率低,燃料消耗多的不足,编队保持控制采用沿航迹向控制方式。
2.1.1 调整δΔe当单独调整δΔe矢量而不改变δΔa时,可以采取两次沿航迹向脉冲控制,喷气时刻为u和u+π,两次喷气量相同,喷气方向相反。单次对应的速度增量为Δve
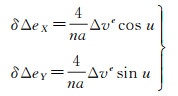 (8)
(8)
式中,n为轨道角速度;喷气时刻u=arctan(δΔeY/δΔeX);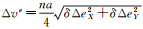
当单独调整相对长半轴δΔa而不改变δΔe时,可以通过两次沿航迹向脉冲控制。两次喷气的时刻分别是u和u+π,两次喷气量相同,喷气方向相同。单次喷气对应速度增量为Δva
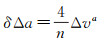 (9)
(9)
式中,u为任意纬度幅角。
2.1.3 改变δΔu当需要独立改变δΔu时,同样可以利用两次沿航迹向脉冲控制实现。两次喷气分别在u和u+2π,两次喷气量相同,喷气方向相反。单次喷气对应速度增量为Δvu
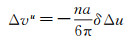 (10)
(10)
根据前面分析,可以得出以下两点结论:
(1) 相对半长轴、相对偏心率矢量及相对纬度幅角的联合调整可以通过3次相位间隔180°的沿航迹向脉冲控制实现。第1次喷气是在纬度幅角u1=arctan(δΔeY/δΔeX)的时刻,喷气量将产生的沿航迹向速度增量是Δv1=Δve+Δva+Δvu;第2次喷气在纬度幅角为u2=arctan(δΔeY/δΔeX)+π的时刻,喷气量将产生的切向速度增量是Δv2=-Δve+Δva;同样,第3次喷气是在纬度幅角为u3=arctan(δΔeY/δΔeX)+2π的时刻,喷气量将产生的切向速度增量是Δv3=-Δvu。
(2) 调整δΔe的两次脉冲控制对相对半长轴的改变量为δΔue=3π/4δ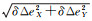
假定相对轨道根数调整量为δΔa、δΔe和δΔu,由于编队控制过程相对轨道根数之间耦合影响,需要对δΔu控制量进行如下补偿
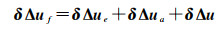 (11)
(11)
式中,δΔuf为最终的调整量,因此可以得到3脉冲编队控制公式
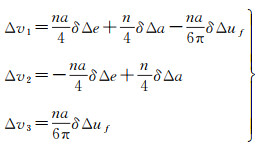 (12)
(12)
将式(11)代入式(12)中,可得
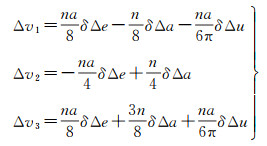 (13)
(13)
实际上,编队控制触发时刻与编队控制时刻往往不一致,因此还需要对δΔu控制量进行修正。记触发时刻对应的纬度幅角为u0,则到达第1次控制时刻u1,由半长轴差引起航迹方向漂移对应的相对纬度幅角变化量dΔu为
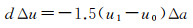 (14)
(14)
将式(14)代入式(13)中,可进一步得到
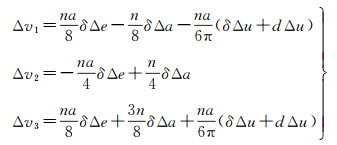 (15)
(15)
考虑到编队相对运动可以分解为沿航迹向与垂直沿航迹向两个独立平面运动的叠加,故而相应的面内控制与面外控制是独立的,可以进行解耦控制。
平面外采用1脉冲控制,喷气方向为正法向,控制时刻为
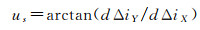 (16)
(16)
控制量为
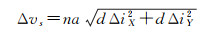 (17)
(17)
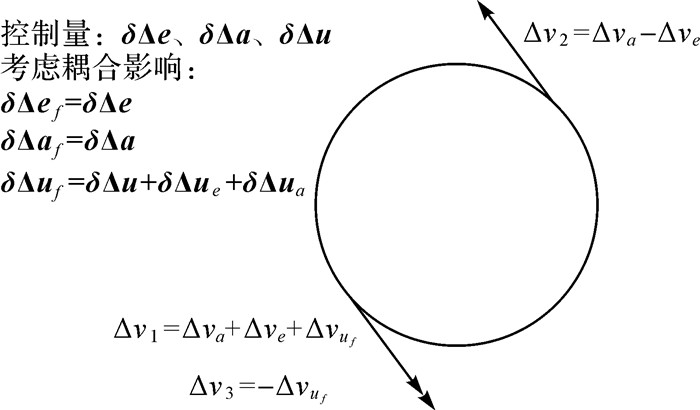
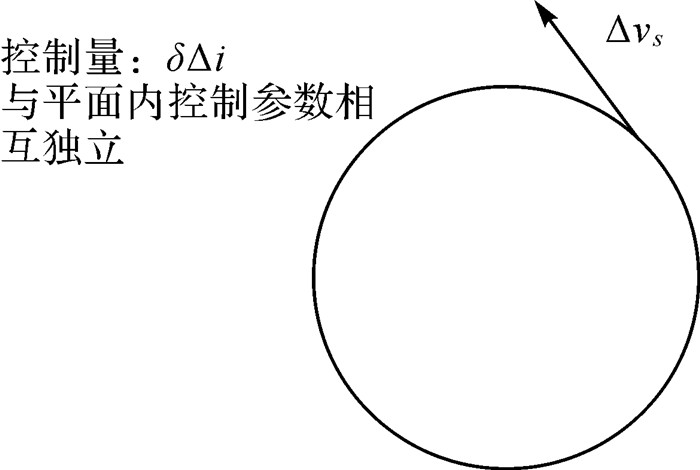
由上述算法推导可以得到平面内与平面外独立两组共四脉冲编队保持控制策略。其中,面内三脉冲控制分别在u1、u1+π及u1+2π时刻触发,逐次控制量为考虑相对轨道根数耦合影响的速度脉冲Δv1、Δv2与Δv3,具体控制过程如图 1所示;面外倾角矢量由于采用法向推力器,故而可与面内参数独立解耦控制,触发时刻us、速度脉冲Δvs,具体控制过程如图 2所示。
|
| 图 1 编队保持面内控制过程 Fig. 1 In-track plane control process of the formation |
|
| 图 2 编队保持面外控制过程 Fig. 2 Out-track plane control process of the formation |
进一步,从理论分析及算法推导角度可以得到本文提出的控制策略具备如下先进性:
(1) 高控制效率、低工程复杂度。由编队相对动力学方程(5)变换可以得到如下近圆轨道卫星简化的高斯方程
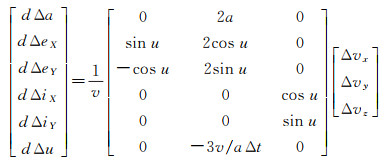 (18)
(18)
由上述公式易见,在面内参数Δe矢量调整方面,本文方法采用的航迹向推力器是径向推力器控制效率的2倍,故而与传统使用径向推力器的三脉冲、五脉冲控制算法相比,一方面简化了推力器安装,降低了工程复杂度,一方面提高了控制效率,节省了燃料消耗。
(2) 无偏控制方法、高控制精度。首先,结合式(5)分析,采用轨道面内根数(δΔe、δΔa、δΔu)联合控制与轨道面外根数(δΔi)独立控制相结合的策略,与TanDEM任务和PRISMA任务所采用的主动偏置半长轴实现相对纬度幅角漂移控制不同,本文方法实现了编队参数的无偏控制,减小了相同控制周期内构形发散尺度,为InSAR任务提供了精确稳定的干涉基线。其次,由式(15)的推导过程易见,本文方法通过对编队控制过程中相对轨道根数δΔa、δΔe和δΔu间耦合影响以及触发时刻与控制时刻不一致等误差因素影响进行了补偿,相比较于其他方法,具有更高的控制精度。
(3) 控制策略参数化,便于工程实现。由文中考虑补偿控制过程中相对轨道根数间耦合影响的平面内控制时刻u1、u2、u3、速度脉冲Δv1、Δv2、Δv3以及平面外控制时刻us、速度脉冲Δvs参数化形式可见,控制量完全由编队构形参数变化量决定,物理意义明确,便于工程计算与实施。
该方法已成功应用于天绘二号双星在轨编队构形控制。
3 试验验证本节将采用本文提出的编队构形控制方法开展试验验证,假定主星在轨道高度520 km的近圆太阳同步轨道。编队构形采用等半长轴和等倾角的设计,标称编队构形参数见表 1,编队控制间隔周期为1 d。控制过程中空间轨迹和部分相对构形参数变化如图 3、图 4所示。
| 相对构形参数 | 取值 |
| p/m | 248 |
| s/m | 1230 |
| θFF/(°) | 90 |
| φFF/(°) | 90 |
| l/m | 0 |

|
| 图 3 编队保持控制过程空间轨迹 Fig. 3 Tracks of the formation maintenance |
|
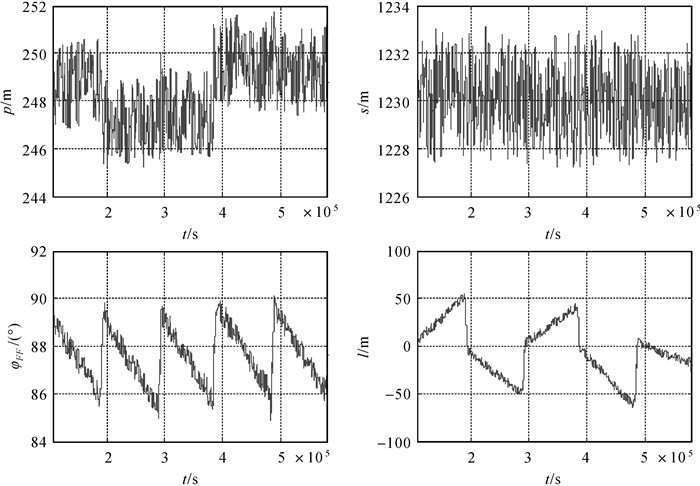
| 图 4 编队构形参数的变化曲线 Fig. 4 Variation of the formation configuration parameter |
仿真过程中考虑J2与大气摄动影响,主要误差项包括:相对导航误差、推力器效率误差和控制时间误差。其中,相对导航误差将对编队控制算法生成的控制量产生直接影响,对编队控制误差传递是按控制策略生成方式等比例传递的;推力器效率误差主要是由推力器安装误差、推力变化、推力偏斜等因素引起的推力器效率误差,该误差可以通过在轨标定使其减少。天绘二号卫星经过标定后的推力器效率误差保持在1%以内,即推力器效率误差引起的控制误差为所需控制量的1%;天绘二号卫星编队控制时间的分辨率为1 ms,这样时间分辨率引起的控制时间误差最大为1 ms。根据上述分析,误差项引起的编队控制最大误差包络见表 2。
| 参数 | 相对导航误差 | 推力器效率误差 | 控制时间误差 |
| Δp/m | 1.90 | 3.71 | 0.002 5 |
| Δs/m | 2.8 | 1.53 | 0.001 3 |
| ΔθFF/(°) | 0.5 | 1.22 | 0.000 09 |
| ΔφFF/(°) | 0.3 | 1.10 | 0.000 025 |
| Δl/m | 4.9 | 7.28 | 0.36 |
天绘二号卫星2021年4月至10月实际在轨编队保持控制精度均值统计见表 3,全球框架下垂直有效基线与沿航迹向基线[25-26]变化情况如图 5、图 6所示。
| 参数 | 控制误差均值 |
| Δp/m | 2.53 |
| Δs/m | 1.81 |
| ΔθFF/(°) | 0.89 |
| ΔφFF/(°) | 0.28 |
| Δl/m | 5.35 |
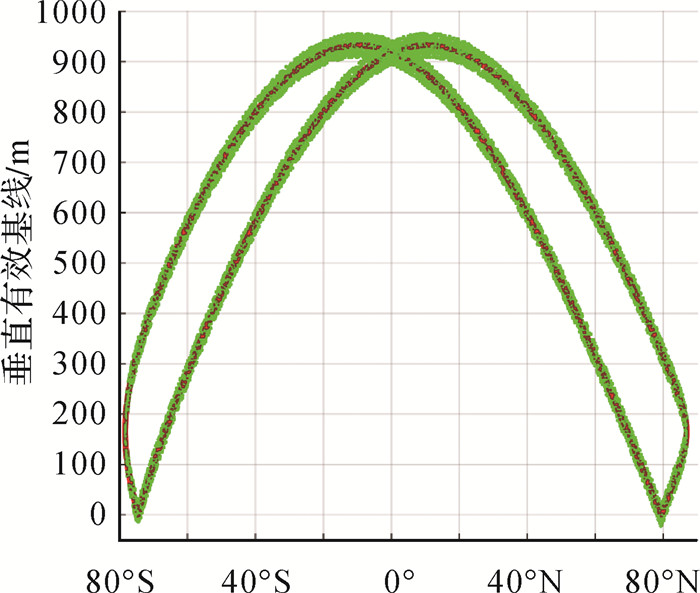
|
| 图 5 全球框架垂直有效基线控制周期内变化情况 Fig. 5 Variation of vertical effective baseline within control cycle under the global framework |
|
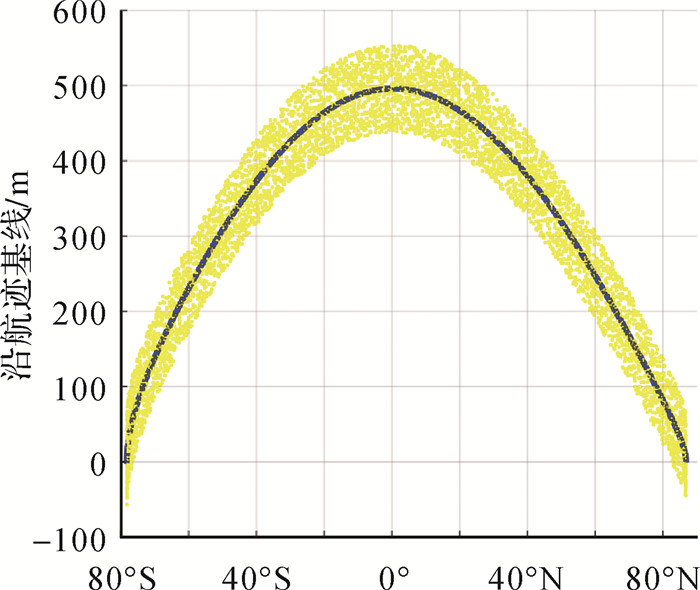
| 图 6 全球框架沿航迹向基线控制周期内变化情况 Fig. 6 Variation of along track baseline within control cycle under the global framework |
由结果可见,编队保持精度优于仿真误差最大包络,可以有效将全球框架下的双星垂直有效基线与沿航迹向基线分别保持在80、50 m变化预期包络范围内,编队保持控制策略合理有效。
4 结论针对InSAR卫星编队构形保持控制问题,本文引入相对轨道根数的编队动力学描述,通过Hill坐标系面内、面外控制隔离,优化设计了一种四脉冲编队保持控制方法,并制定了相应的控制策略。该方法具有如下优点:
(1) 相比较于传统三脉冲、五脉冲编队控制,该方法面内控制仅需沿航迹向脉冲,一方面无须安装径向推力器,降低了工程复杂度,一方面沿航迹向为径向控制效率的2倍,控制效率高、节省燃料。
(2) 该方法通过对编队控制过程中相对轨道根数耦合影响以及触发时刻与控制时刻不一致等误差因素的影响进行补偿,因此相比较于其他方法,具有更高的控制精度。
(3) 该方法求解过程简单,物理意义明确,控制量完全由编队构形参数变化量决定,能够完成编队保持控制任务。
该编队保持方法已成功应用于天绘二号卫星,并经过在轨验证,控制精度满足预期指标,全球框架下的垂直有效基线与沿航迹基线分布满足预期,有效保证了InSAR任务的顺利开展。
| [1] |
姜卫平, 赵伟, 赵倩, 等. 新一代探测地球重力场的卫星编队[J]. 测绘学报, 2014, 43(2): 111-117. JIANG Weiping, ZHAO Wei, ZHAO Qian, et al. Satellite formation for a new gravity field exploration mission[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(2): 111-117. |
| [2] |
杨元喜, 王建荣, 楼良盛, 等. 航天测绘发展现状与展望[J]. 中国空间科学技术, 2022, 42(3): 1-9. YANG Yuanxi, WANG Jianrong, LOU Liangsheng, et al. Development status and prospect of satellite-based surveying[J]. Chinese Space Science and Technology, 2022, 42(3): 1-9. |
| [3] |
MASSONNET D. Capabilities and limitations of the interferometric cartwheel[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(3): 506-520. DOI:10.1109/36.911109 |
| [4] |
PETERSON E H, FOTOPOULOS G, ZEE R E. A feasibility assessment for low-cost InSAR formation-flying microsatellites[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(8): 2847-2858. DOI:10.1109/TGRS.2009.2017521 |
| [5] |
OCHS S, PITZ W. The TerraSAR-X and TanDEM-X satellites[C]//Proceedings of the 3rd International Conference on Recent Advances in Space Technologies. Istanbul, Turkey: 2007, IEEE: 294-298.
|
| [6] |
HUANG Chengquan, GONG Weishu, PANG Yong. Remote sensing and forest carbon monitoring: a review of recent progress, challenges and opportunities[J]. Journal of Geodesy and Geoinformation Science, 2022(2): 124-147. |
| [7] |
LI Zhenhong, YU Chen, XIAO Ruya, et al. Entering a new era of InSAR: advanced techniques and emerging applications[J]. Journal of Geodesy and Geoinformation Science, 2022, 5(1): 1-4. |
| [8] |
YAO Yibin, YANG Yuanxi, SUN Heping, et al. Geodesy discipline: progress and perspective[J]. Journal of Geodesy and Geoinformation Science, 2021, 4(4): 1-10. |
| [9] |
ZINK M, BARTUSCH M, MILLER D. TanDEM-X mission status[C]//Proceedings of 2011 IEEE International Geoscience and Remote Sensing Symposium. Vancouver, BC, Canada: IEEE, 2011: 2290-2293.
|
| [10] |
KROES R, MONTENBRUCK O, BERTIGER W, et al. Precise GRACE baseline determination using GPS[J]. GPS Solutions, 2005, 9(1): 21-31. |
| [11] |
ALLENDE-ALBA G, MONTENBRUCK O. Robust and precise baseline determination of distributed spacecraft in LEO[J]. Advances in Space Research, 2016, 57(1): 46-63. |
| [12] |
KRIEGER G, MOREIRA A, FIEDLER H, et al. TanDEM-X: a satellite formation for high-resolution SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(11): 3317-3341. |
| [13] |
GILL E, D'AMICO S, MONTENBRUCK O. Autonomous formation flying for the PRISMA mission[J]. Journal of Spacecraft and Rockets, 2007, 44(3): 671-681. |
| [14] |
孟云鹤, 戴金海. 近圆轨道卫星编队捕获技术研究[J]. 空间科学学报, 2006, 26(2): 148-154. MENG Yunhe, DAI Jinhai. Satellite formation establishing in near circular orbit[J]. Chinese Journal of Space Science, 2006, 26(2): 148-154. |
| [15] |
贺东雷, 曹喜滨, 马骏, 等. 基于相对偏心率/倾角矢量的编队控制方法[J]. 系统工程与电子技术, 2011, 33(4): 833-837. HE Donglei, CAO Xibin, MA Jun, et al. Formation control approach based on relative eccentricity/inclination vector[J]. Systems Engineering and Electronics, 2011, 33(4): 833-837. |
| [16] |
楼良盛, 刘志铭, 张昊, 等. 天绘二号卫星工程设计与实现[J]. 测绘学报, 2020, 49(10): 1252-1264. LOU Liangsheng, LIU Zhiming, ZHANG Hao, et al. TH-2 satellite engineering design and implementation[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(10): 1252-1264. DOI:10.1947/j.AGCS.2020.20200175 |
| [17] |
D'AMICO S, MONTENBRUCK O. Proximity operations of formation-flying spacecraft using an eccentricity/inclination vector separation[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(3): 554-563. |
| [18] |
孙俊, 黄静, 张宪亮, 等. 地球轨道航天器编队飞行动力学与控制研究综述[J]. 力学与实践, 2019, 41(2): 117-136. SUN Jun, HUANG Jing, ZHANG Xianliang, et al. Dynamics and control of spacecraft formation flying in earth orbit[J]. Mechanics in Engineering, 2019, 41(2): 117-136. |
| [19] |
胡敏, 曾国强, 姚红. 基于相对轨道根数的卫星编队重构控制研究[J]. 装备指挥技术学院学报, 2010, 21(1): 74-77. HU Min, ZENG Guoqiang, YAO Hong. Research on satellite formation reconfiguration control based on relative orbit elements[J]. Journal of the Academy of Equipment Command & Technology, 2010, 21(1): 74-77. |
| [20] |
崔海英, 李俊峰, 高云峰. 椭圆参考轨道的卫星编队队形保持控制设计[J]. 工程力学, 2007, 24(4): 147-151. CUI Haiying, LI Junfeng, GAO Yunfeng. Control of satellite formation keeping in eccentric orbits[J]. Engineering Mechanics, 2007, 24(4): 147-151. |
| [21] |
张世杰, 段广仁. 分布式卫星编队飞行队形保持协同控制[J]. 宇航学报, 2011, 32(10): 2140-2145. ZHANG Shijie, DUAN Guangren. Cooperative control for distributed satellite formation keeping[J]. Journal of Astronautics, 2011, 32(10): 2140-2145. |
| [22] |
张杨, 侯明善, 刘永刚. 卫星编队长期保持与控制比较研究[J]. 计算机仿真, 2009, 26(11): 41-45. ZHANG Yang, HOU Mingshan, LIU Yonggang. A comparison of long-term keeping and control for satellite formation flying[J]. Computer Simulation, 2009, 26(11): 41-45. |
| [23] |
曹喜滨, 贺东雷. J2摄动下编队构形保持脉冲控制方法[J]. 系统仿真学报, 2007, 19(23): 5447-5450. CAO Xibin, HE Donglei. Impulsive control approach for formation keeping under J2 perturbation[J]. Journal of System Simulation, 2007, 19(23): 5447-5450. |
| [24] |
D'AMICO S, ARDAENS J S, LARSSON R. Spaceborne autonomous formation-flying experiment on the PRISMA mission[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(3): 834-850. |
| [25] |
楼良盛, 刘志铭, 李崇伟. 卫星编队InSAR基线的确定方法[J]. 遥感信息, 2013, 28(2): 9-11, 23. LOU Liangsheng, LIU Zhiming, LI Chongwei. Technique of determining baseline for InSAR based on formation-flying satellites[J]. Remote Sensing Information, 2013, 28(2): 9-11, 23. |
| [26] |
TANG Xinming, LI Tao, GAO Xiaoming, et al. Research on key technologies of precise InSAR surveying and mapping applications using automatic SAR imaging[J]. Journal of Geodesy and Geoinformation Science, 2019, 2(1): 27-37. |



