2. 中国气象局气象探测中心, 北京 100081;
3. 北京航空航天大学卫星导航与移动通信融合技术工业和信息化部重点实验室, 北京 100191;
4. 南宁师范大学地理与海洋研究院, 广西 南宁 530001
2. Meteorological Observation Centre of CMA, Beijing 100081, China;
3. Laboratory of Navigation and Communication Fusion Technology, Ministry of Industry and Information Technology, Beihang University, Beijing 100191, China;
4. Institute of Geography and Oceanography, Nanning Normal University, Nanning 530001, China
对流层延迟是全球卫星导航系统(GNSS)、甚长基线干涉测量(very long baseline interferometry,VLBI)、卫星激光测距(satellite laser ranging,SLR)、卫星测高等空间大地测量技术实现高精度参数估计的主要误差源之一,在数据处理中可利用外部数据产品估算对流层延迟并予以改正[1-3]。全球大气再分析产品,如欧洲中尺度天气预报中心(European Centre for Medium-range Weather Forecasts,ECMWF)再分析中间产品(ECMWF reanalysis interim,ERA-Interim,简称“ERAI”)和第5代产品(the fifth generation ECMWF reanalysis,ERA5)、美国国家环境预报中心再分析产品(The United States National Centers for environmental prediction reanalysis,NCEP),通过同化多源历史气象观测资料,具有精度高、时空覆盖完整的优点[4],被广泛用于对流层天顶延迟(zenith path delay,ZPD)和斜路径延迟(slant path delay,SPD)的计算及建模[5-8],发布了一系列ZPD经验模型(如SHAO系列模型[9]、IGGtrop系列模型[10]、TropGrid系列模型[11]、ITG模型[12]、GTrop模型[13]和HGPT模型[14])和映射函数模型(如UNB-VMF1[15]、VMF3[16]和GFZ-VMF1[17])。
2013年11月,中国气象局启动了我国的全球大气再分析计划,总体目标是建成我国第1代全球大气再分析业务系统,并建成跨度40 a(1979—2018)的中国第1代全球大气/陆面再分析产品(China’s first generation 40 a global atmosphere and land reanalysis,CRA40)[18-19],质量超过国际第2代,在中国区域接近或达到国际第3代大气再分析水平(http://data.cma.cn/analysis/cra40)。2020年12月CRA40产品正式上线并业务化发布[20]。探讨利用CRA40进行对流层延迟计算的方法,并评估CRA40用于对流层延迟计算的精度,尤其是在中国区域的精度,具有重要的意义。文献[21]针对CRA40在中国区域GNSS水汽反演中的应用,对2016年全年CRA40和ERA5的气温、气压、大气水汽加权平均温度和天顶总延迟(zenith total delay,ZTD)进行了较为系统的比较评估,结果表明以GNSS ZTD为参考,CRA40 ZTD精度为1.35 cm,总体较ERA5差。但文献[21]主要讨论的是中国区域的天顶延迟结果,并未开展全球范围内包括斜路径延迟在内的对流层延迟的系统评估。
本文主要对基于CRA40计算的对流层延迟开展系统的评估工作,首先讨论基于CRA40采用射线追踪技术计算对流层延迟的方法,然后分别在231个国际GNSS服务(international GNSS service,IGS)站和213个中国大陆构造环境监测网络(crustal movement observation network of China,CMONOC)站处对ERAI、ERA5和CRA40对流层延迟计算精度(ZPD和5°高度角SPD)进行系统比较评估,并对中国区域CRA40对流层湿延迟计算精度的变化特征进行分析。
1 数据与方法 1.1 CRA40产品及预处理CRA40(1979—2018)是由中国气象局国家气象信息中心牵头,联合多家单位开发的,整体经历了两个阶段,即准备阶段(2014—2016年)和实施阶段(2016—2019年)[20]。准备阶段主要完成历史气象观测资料的准备和模式同化系统的建设[22-23],实施阶段主要完成CRA-Interim(2006年7月—2016年12月)产品的制作和评估及CRA40产品的研制[24-26]。CRA40产品是分10段进行研制的,每段4.5 a,段与段之间有半年重叠,以保证产品的连续性。2019年8月全部40 a CRA40再分析产品研制完成,并于2020年12月正式上线业务化[20]。本文采用CRA40气压层产品进行对流层延迟计算,产品模式同化系统为GFS/GSI-3Dvar,时间分辨率为6 h。产品水平格网采用高斯经纬度投影,经向为均匀网格划分,分辨率为0.312 5°,纬向为非均匀网格划分,分辨率在0.312 5°左右。选用参数包括位势高、温度和比湿,位势高和温度参数气压层层数为47,层顶气压为1 hPa(42 km左右),比湿参数气压层层数为37,层顶气压为100 hPa(16 km左右)。
相关研究表明:同一再分析产品随着水平分辨率的提高,射线追踪的计算效率会显著降低,而对射线追踪ZTD计算精度的影响并不显著[7],因此综合考虑射线追踪计算效率和精度,本文采用NCEP官网提供的wgrib2工具利用双线性插值方法将再分析资料的水平分辨率统一重采样为1°,来开展后续的再分析资料评估试验。此外,CRA40比湿参数仅有37层,与位势高和温度参数气压层层数不一致,因此需要对比湿参数层顶100 hPa以上气压层(1、2、3、5、7、10、20、30、50、70 hPa)的比湿参数进行处理,得到气压层层数为47的比湿参数。可选的处理方法主要有3种:方法1认为100 hPa(16 km)以上水汽已经相当稀疏,因此,可以简单地将100 hPa以上气压层的比湿参数值设为0 g·kg-1;方法2由现有层顶100 hPa和相邻气压层(如125、150、175 hPa等)的比湿参数来线性外推层顶以上的比湿参数;方法3直接采用100 hPa的比湿参数值作为其他层顶气压层的数值。
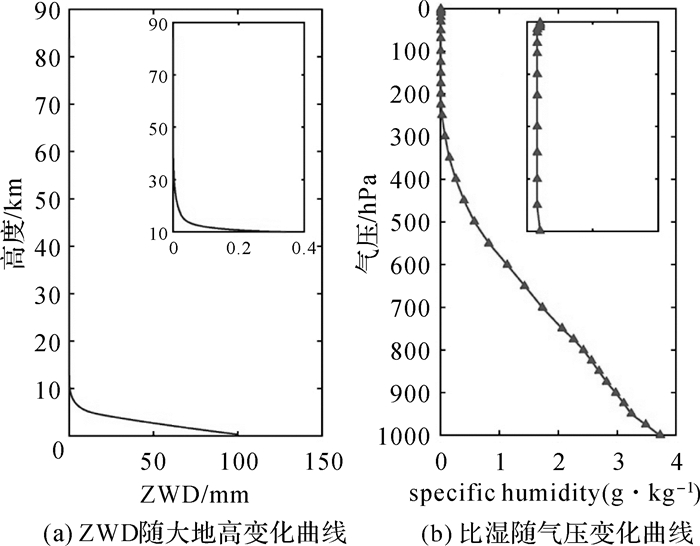
为评估以上方法的差异,图 1(a)给出了2018年7月19日UTC 15时BZRG测站基于ERA5计算的天顶湿延迟(zenith wet delay,ZWD)随高度的变化曲线,图 1(b)给出了2018年7月ERA5月平均产品全球比湿参数均值随气压(37层)的变化曲线。由图 1可知,16 km(100 hPa)以上ZWD数值在亚毫米量级,100 hPa以上比湿参数并不为0,几乎处于一个不变值,因此方法1可行但不严密,而方法3相对更为合理。相比之下,方法2利用层顶100 hPa和相邻气压层比湿来线性外推顶层比湿,可能会得到小于0 g·kg-1的比湿。综合考虑计算的可行性和合理性,本文采用方法3处理顶层比湿参数。经预处理后,CRA40产品时间和水平分辨率分别为6 h和1.0°,气压层层数为47,层顶气压为1 hPa(42 km)。
|
| 图 1 ZWD随高度和比湿随气压的变化曲线 Fig. 1 Changing curves of ZWD with height and specific humidity with pressure |
1.2 ERA5和ERAI产品
ERA5(1950年至今)是ECMWF发布的最新一代全球大气再分析产品,产品模式同化方法为Ensemble of 4D-Var,时间延迟在5 d左右,时间分辨率为1 h,水平分辨率为31 km,气压层产品垂直层数为37[27-28]。ERAI(1979—2019年)是ERA5的上一代全球大气再分析产品,产品模式同化方法为4D-Var,时间分辨率为6 h,水平分辨率为80 km,气压层产品垂直层数为37[29]。本文选用ERA5和ERAI气压层产品进行对流层延迟计算,参数包括位势、温度和比湿,产品时间和水平分辨率与CRA40重采样产品保持一致,分别为6 h和1.0°,层顶气压为1 hPa。
1.3 基于射线追踪技术的对流层延迟计算方法组合使用再分析产品(0~42 km)和美国标准大气模型(COESA 1976)(42~84 km)来实现参数的中性大气层全覆盖[30]。依据文献[31]给出的方法,采用EGM2008模型[32]将再分析位势高/位势转换成大地高。利用文献[33]给出的方法将再分析比湿转换为水汽压。采用文献[34]给出的大气垂直分层方法(0~2 km:10 m间隔;2~6 km:20 m间隔;6~16 km:50 m间隔;16~36 km:100 m间隔;36~84 km:500 m间隔)来进行垂直大气细化分层。分别使用线性、指数和指数插值方法将温度、气压和水汽压由等压层内插到细化高度层[30]。以温度、气压和水汽压为输入,通过式(1)来计算静力学折射率(nh)、湿折射率(nw)和总折射率(n)[35]
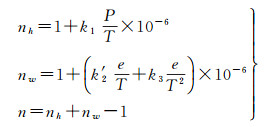 (1)
(1)
式中, k1、k′2和k3为常数,取值分别为77.689 K/hPa、22.974 2 K/hPa和375 463 K2/hPa[36]。P(hPa)、T(K)和e(hPa)分别为气压、温度和水汽压。选用二维分段线性射线追踪方法来确定射线传播路径[30, 37],之后利用式(2)计算ZPD和SPD[38]
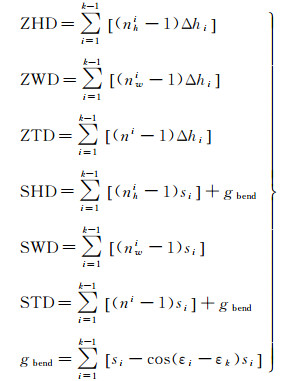 (2)
(2)
式中,ZHD为天顶静力学延迟(zenith hydrostatic delay); SHD为斜路径静力学延迟(slant hydrostatic delay); SWD为斜路径湿延迟(slant wet delay); STD为斜路径总延迟(slant total delay);ZHD、ZWD和ZTD统称为ZPD,SHD、SWD和STD统称为SPD;k为高度层层数;nhi、nwi和ni表示第i层和第i+1层的静力学折射率、湿折射率和总折射率均值;Δhi表示第i层和第i+1层的高差;si表示夹在第i层和第i+1层间的射线路径长度;gbend表示几何弯曲项;εi表示第i层处射线路径的高度角;εk为第k层(射线穿出层)射线路径的高度角。
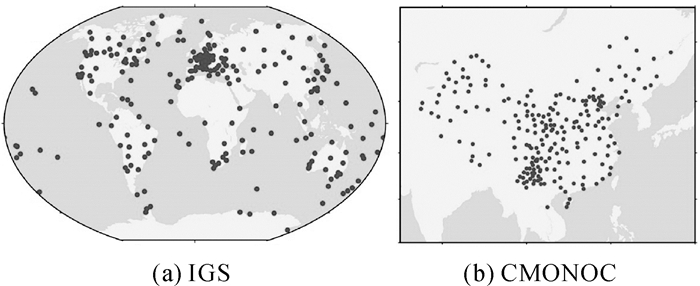
分别以6 h和1.0°时空分辨率的CRA40(47层)、ERA5(37层)和ERAI(37层)再分析温度、比湿和位势高/位势为输入,采用前述的对流层延迟射线追踪方法,计算2018年全年全球231个IGS站处(图 2(a))和国内213个CMONOC站处(图 2(b))的ZPD和5°高度角、16个方位角(0°~337.5°,间隔22.5°)下的SPD。取16个方位角的SPD均值作为5°高度角的SPD。最终得到3种再分析产品在所有选定测站处2018年时间分辨率为6 h的ZPD和5°高度角SPD产品。
|
| 图 2 IGS和CMONOC站点分布 Fig. 2 Distribution of selected IGS and CMONOC stations |
2 对流层天顶总延迟精度评估
事后GNSS ZTD未被CRA40、ERAI和ERA5同化[26-29],因此可以将其作为独立参考,来评估基于再分析资料计算的ZTD精度。从IGS官方FTP(gdc.cddis.eosdis.nasa.gov)下载2018年全年选定231个IGS站处时间分辨率为5 min的ZTD产品,产品统计精度可达4 mm[39](https://www.igs.org/products#about)。采用PANDA软件和文献[40]所示的数据处理策略对所有选定213个CMONOC测站的GNSS观测数据进行事后精密单点定位(precise point positioning,PPP)处理[41],得到选定CMONOC测站2018年全年时间分辨率为1 h的ZTD产品,产品统计精度优于5 mm[40]。
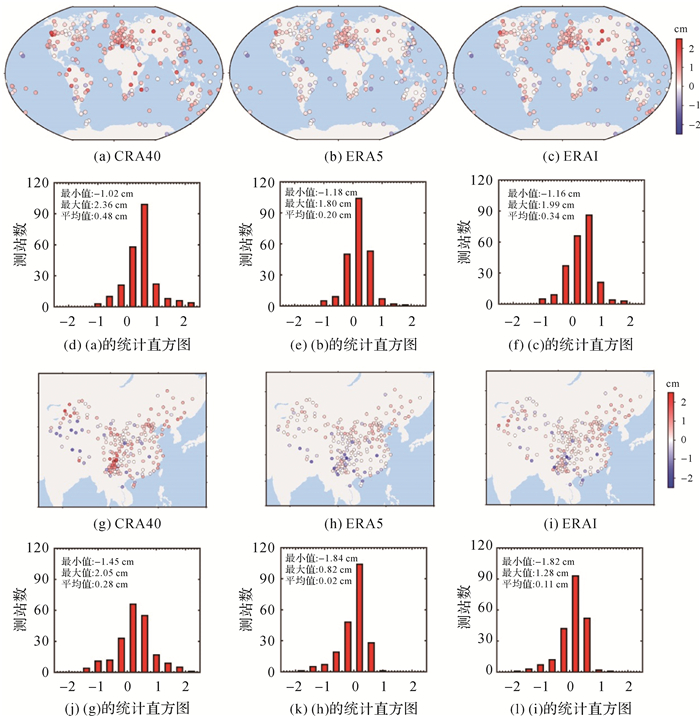
以GNSS ZTD为参考,统计2018年全年每个选定测站基于再分资料计算的ZTD误差偏差(Bias)和均方根(root mean square,RMS)。图 3给出了全球范围(IGS站网)和中国区域(CMONOC站网)基于3种再分析产品的ZTD Bias地理分布和直方图,图 3(a)、(b)和(c)给出全球范围CRA40、ERA5和ERAI的ZTD Bias分布,图 3(d)、(e)和(f)给出相应的统计直方图,图 3(g)、(h)和(i)给出中国区域CRA40、ERA5和ERAI的ZTD Bias分布,而图 3(j)、(k)和(l)则给出相应的统计直方图。在全球范围,ERA5 ZTD Bias平均最小,均值为0.20 cm(图 3(b)、(e))。ERAI ZTD Bias所有测站均值为0.34 cm,ZTD偏大的测站主要分布在欧洲、中亚、北美等地区(图 3(c)、(f))。相比之下,CRA40 ZTD Bias最大,均值为0.48 cm,主要出现在欧洲、北美及赤道区域(图 3(a)、(d))。
|
| 图 3 ZTD差值Bias分布和直方图 Fig. 3 Distribution and histogram of ZTD Bias |
在中国区域,ERA5 ZTD Bias仍然最小,均值为0.02 cm(图 3(h)、(k))。ERAI ZTD Bias次之,均值为0.11 cm(图 3(i)、(l))。CRA40 ZTD Bias同样最大,平均为0.28 cm,川滇地区、新疆北部的ZTD正偏差较为明显,负偏差则主要出现在新疆南部区域(图 3(g)、(j))。再分析ZTD整体偏差均为正,表明再分析ZTD与GNSS ZTD间可能存在系统性偏差(再分析ZTD数值偏大),文献[42—43]也给出了类似的结果。
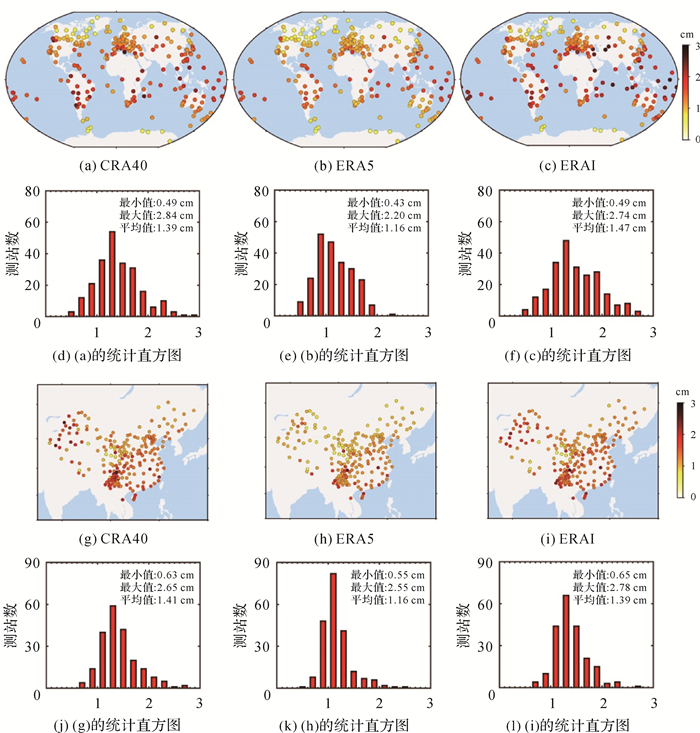
除了平均偏差外,图 4也相应地给出了基于3种再分析资料计算的ZTD RMS地理分布和直方图,图 4(a)、(b)和(c)分别给出全球范围CRA40、ERA5和ERAI的ZTD RMS分布,图 4(d)、(e)和(f)分别给出相应的统计直方图,图 4(g)、(h)和(i)分别给出中国区域CRA40、ERA5和ERAI的ZTD RMS分布,而图 4(j)、(k)和(l)则给出相应的统计直方图。在全球范围,再分析ZTD RMS与测站纬度相关,赤道及其附近区域RMS明显偏大,这主要是受赤道及其附近区域含量丰富且变化剧烈水汽的影响[44]。ERA5 ZTD RMS整体最小,平均为1.16 cm(图 4(b)、(e))。CRA40 ZTD RMS次之,平均为1.39 cm,其中赤道及其附近区域相比ERA5 RMS明显更大(图 4(a)、(d))。ERAI ZTD RMS整体最大,平均为1.47 cm,RMS较大的测站主要分布在赤道及其附近区域以及中东、中亚等地区(图 4(c)、(f))。
|
| 图 4 ZTD差值RMS分布和直方图 Fig. 4 Distribution and histogram of ZTD RMS |
在中国区域,ERA5 ZTD RMS仍然最好,均值为1.16 cm(图 4(h)、(k))。ERAI ZTD RMS次之,川滇地区以及新疆、河北、山东、辽宁等地均相对ERA5明显变差,均值为1.39 cm(图 4(i)、(l))。CRA40 ZTD RMS相对ERAI略差,主要集中在川滇地区和新疆,均值为1.41 cm(图 4(g)、(j))。整体统计上,ERA5 ZTD RMS明显小于CRA40和ERAI,而CRA40和ERAI ZTD RMS比较接近,表明ERA5 ZTD精度显著优于ERAI和CRA40,而ERAI和CRA40 ZTD精度相近。
3 对流层斜路径延迟精度评估由于斜路径延迟缺乏可靠的参考,无法直接对基于再分析资料计算的SPD绝对精度进行评估,而对流层天顶总延迟精度评估结果显示ERA5 ZTD精度最高,理论上ERA5计算的ZPD和SPD精度也最高,因此就以ERA5计算的ZPD和SPD为参考,来评估CRA40和ERAI计算的ZPD和SPD精度。首先计算2018年全年所有选定测站CRA40和ERAI ZPD和SPD同ERA5 ZPD和SPD的差异Bias和RMS,然后统计出差异Bias和RMS的最小值(min)、最大值(max)和均值(mean),结果见表 1。
| 再分析产品 | 对流层延迟 | 全球范围(IGS站网) | 中国区域(CMONOC站网) | |||||||||||||
| Bias | RMS | Bias | RMS | |||||||||||||
| min | max | mean | min | max | mean | min | max | mean | min | max | mean | |||||
| CRA40-ERA5 | ZTD | -1.21 | 2.43 | 0.28 | 0.26 | 2.72 | 1.04 | -1.29 | 2.58 | 0.25 | 0.47 | 2.91 | 1.18 | |||
| ZHD | -0.30 | 0.41 | -0.02 | 0.05 | 0.44 | 0.13 | -0.30 | 0.37 | 0.02 | 0.08 | 0.47 | 0.14 | ||||
| ZWD | -1.28 | 2.31 | 0.30 | 0.21 | 2.64 | 1.04 | -1.33 | 2.62 | 0.23 | 0.46 | 2.96 | 1.16 | ||||
| STD | -13.44 | 25.92 | 2.84 | 2.71 | 28.93 | 10.83 | -14.37 | 28.25 | 2.58 | 5.03 | 31.57 | 12.30 | ||||
| SHD | -3.24 | 3.43 | -0.31 | 0.48 | 3.87 | 1.37 | -3.52 | 4.02 | 0.17 | 0.76 | 5.14 | 1.49 | ||||
| SWD | -14.06 | 24.68 | 3.16 | 2.19 | 28.21 | 10.80 | -14.48 | 29.10 | 2.41 | 4.94 | 32.43 | 12.13 | ||||
| ERAI-ERA5 | ZTD | -1.25 | 1.45 | 0.14 | 0.20 | 2.37 | 1.06 | -0.65 | 0.94 | 0.08 | 0.55 | 1.94 | 1.03 | |||
| ZHD | -0.20 | 0.14 | -0.02 | 0.05 | 0.27 | 0.10 | -0.21 | 0.44 | 0.00 | 0.07 | 0.65 | 0.13 | ||||
| ZWD | -1.05 | 1.50 | 0.15 | 0.18 | 2.41 | 1.05 | -0.71 | 0.99 | 0.08 | 0.53 | 1.94 | 1.02 | ||||
| STD | -13.59 | 14.78 | 1.47 | 2.17 | 25.04 | 11.11 | -7.02 | 10.10 | 0.87 | 6.02 | 20.74 | 10.82 | ||||
| SHD | -2.30 | 1.38 | -0.2 | 0.49 | 3.00 | 1.04 | -2.36 | 4.23 | -0.02 | 0.66 | 6.67 | 1.39 | ||||
| SWD | -11.29 | 15.41 | 1.67 | 1.93 | 24.99 | 11.04 | -7.69 | 10.72 | 0.89 | 5.82 | 20.22 | 10.65 | ||||
由表 1可知,5°高度角SPD差异Bias和RMS约是相应ZPD差异RMS的10倍,这是因为5°高度角SPD和ZPD比值是在10.2左右[45]。CRA40和ERA5对流层延迟差异主要体现在湿延迟部分。全球范围(IGS站网)CRA40和ERA5对流层延迟(ZPD和SPD)差异RMS分别为1.04(ZTD)、0.13(ZHD)、1.04(ZWD)、10.83(STD)、1.37(SHD)和10.80 cm(SWD),中国区域(CMONOC站网)为1.18、0.14、1.16、12.30、1.49和12.13 cm。以ERA5对流层延迟为参考,在全球范围CRA40同ERAI的对流层延迟计算精度基本相当,而在中国区域ERAI对流层延迟计算精度略优于CRA40,可能原因是CRA40在中国区域同化了一些国内特有的气象观测数据,导致在中国区域CRA40与ERA5在同化数据源上有更大差异。
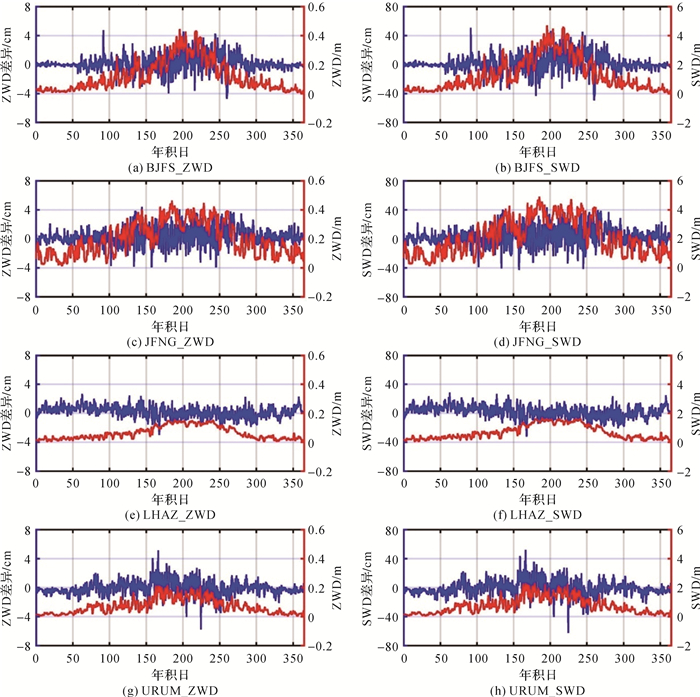
4 中国区域CRA40对流层湿延迟精度变化特征在中国区域CRA40对流层总延迟(ZTD和STD)精度主要取决于湿延迟部分(ZWD和SWD)计算精度,因此重点对中国区域CRA40湿延迟精度的变化特征进行分析。从中国区域选取4个代表性IGS测站,即BJFS(北京房山,温带季风气候)、JFNG(武汉九峰,亚热带季风气候)、LHAZ(拉萨,高原山地气候)和URUM(乌鲁木齐,温带大陆性气候),来分析2018年CRA40 ZWD和SWD精度变化特征,结果如图 5所示。图 5中,横轴表示年积日,纵轴(左,蓝色)表示ZWD/SWD差值,蓝色曲线表示CRA40 ZWD/SWD同ERA5 ZWD/SWD的差值时序,纵轴(右,红色)表示ZWD/SWD,红色曲线表示CRA40 ZWD/SWD时序。
|
| 图 5 2018年BJFS、JFNG、LHAZ和URUM站CRA40 ZWD和SWD差值时序 Fig. 5 Time series of CRA40 ZWD and SWD differences at BJFS, JFNG, LHAZ and URUM stations in 2018 |
由图 5可知,同一站点的ZWD精度变化相位同SWD一致、变化振幅约是SWD的1/10,而不同站点间ZWD和SWD精度变化相位和振幅存在明显差异,主要与站点所处气候类型相关。同属季风气候类型的BJFS和JFNG站,ZWD和SWD精度均有明显的季节变化特征:夏季精度最差,冬季精度最好,且温带BJFS站的ZWD和SWD精度变化振幅明显小于亚热带JFNG站,尤其是在冬季(图 5(a)、(b)、(c)和(d))。高原山地气候的LHAZ站,ZWD和SWD精度全年较为稳定,基本没有季节变化(图 5(e)、(f))。温带大陆性气候的URUM站,ZWD和SWD精度也存在一定的季节变化特征,但变化振幅相对BJFS和JFNG站要小得多(图 5(g)、(h))。
实际上,CRA40 ZWD和SWD精度直接与对流层水汽的含量及变化幅度相关,对流层水汽含量越丰富、变化幅度越剧烈,ZWD和SWD精度就越差,反之亦然。中国区域季风气候区对流层水汽含量及变化幅度夏季大于冬季,因此季风气候区ZWD和SWD精度夏季差于冬季,高原山地气候区对流层水汽含量较低、变化幅度较小,因此高原山地气候区ZWD和SWD精度全年较为稳定。
5 结论与展望本文探讨了基于CRA40采用射线追踪技术计算对流层延迟的方法,在全球范围和中国区域对CRA40、ERAI和ERA5对流层延迟(ZPD和5°高度角SPD)的精度进行了系统比较评估,并对中国区域CRA40 ZWD和SWD精度变化规律进行了分析。结果表明:
(1) 以GNSS ZTD为参考,CRA40 ZTD统计Bias在全球范围和中国区域分别为0.48和0.28 cm;统计RMS约为1.40 cm,在全球范围略优于ERAI,在中国区域基本与ERAI相当,整体上较ERA5差。
(2) 以ERA5 STD为参考,CRA40 STD统计Bias在全球范围和中国区域分别为2.84和2.58 cm;统计RMS在全球范围和中国区域分别为10.83和12.30 cm,同ERAI无明显差异。
(3) 中国区域CRA40 ZWD和SWD精度变化规律与气候类型相关,非季风气候区精度全年较为稳定,季风气候区冬季精度明显优于夏季。
结果证实国产自主可控CRA40产品对流层延迟射线追踪精度基本与第3代全球大气再分析ERAI相当,可以作为可靠的数据源来进行对流层延迟射线追踪、建模等相关研究。本文仅对基于CRA40计算的对流层延迟的精度进行了评估,下一步将利用CRA40对流层延迟进行映射函数、水平梯度建模及北斗/GNSS定位应用研究。
致谢: 感谢ECMWF提供的ERAI和ERA5数据及中国气象局提供的CRA40数据;感谢IGS提供的IGS ZTD产品和中国地震局提供的GNSS观测数据。
| [1] |
NIELL A E. Global mapping functions for the atmosphere delay at radio wavelengths[J]. Journal of Geophysical Research: Solid Earth, 1996, 101(B2): 3227-3246. DOI:10.1029/95JB03048 |
| [2] |
BOEHM J, WERL B, SCHUH H. Troposphere mapping functions for GPS and very long baseline interferometry from European Centre for medium-range weather forecasts operational analysis data[J]. Journal of Geophysical Research Solid Earth, 2006, 111(B2): B02406. |
| [3] |
毛健, 崔铁军, 李晓丽, 等. 融合大气数值模式的高精度对流层天顶延迟计算方法[J]. 测绘学报, 2019, 48(7): 862-870. MAO Jian, CUI Tiejun, LI Xiaoli, et al. A hight-accuracy method for tropospheric zenith delay error correction by fusing atmospheric numerical models[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(7): 862-870. DOI:10.11947/j.AGCS.2019.20190003 |
| [4] |
王旻燕, 姚爽, 姜立鹏, 等. 我国全球大气再分析(CRA-40)卫星遥感资料的收集和预处理[J]. 气象科技进展, 2018, 8(1): 158-163. WANG Minyan, YAO Shuang, JIANG Lipeng, et al. Collection and pre-processing of satellite remote-sensing data in CRA-40 (CMA's global atmospheric reanalysis)[J]. Advances in Meteorological Science and Technology, 2018, 8(1): 158-163. DOI:10.3969/j.issn.2095-1973.2018.01.021 |
| [5] |
ANDREI C O, CHEN R. Assessment of time-series of troposphere zenith delays derived from the global data assimilation system numerical weather model[J]. GPS Solutions, 2009, 13(2): 109-117. DOI:10.1007/s10291-008-0104-1 |
| [6] |
NAFISI V, URQUHART L, SANTOS M C, et al. Comparison of ray-tracing packages for troposphere delays[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(2): 469-481. DOI:10.1109/TGRS.2011.2160952 |
| [7] |
ZHOU Yaozong, LOU Yidong, ZHANG Weixing, et al. Improved performance of ERA5 in global tropospheric delay retrieval[J]. Journal of Geodesy, 2020, 94(10): 1-14. |
| [8] |
BOEHM J, SCHUH H. Vienna mapping functions in VLBI analyses[J]. Geophysical Research Letters, 2004, 31(1): L01603. |
| [9] |
SONG Shuli, ZHU Wenyao, CHEN Qinming, et al. Establishment of a new tropospheric delay correction model over China area[J]. Science China: Physics, Mechanics and Astronomy, 2011, 54(12): 2271-2283. DOI:10.1007/s11433-011-4530-7 |
| [10] |
李薇, 袁运斌, 欧吉坤, 等. 全球对流层天顶延迟模型IGGtrop的建立与分析[J]. 科学通报, 2012, 57(15): 1317-1325. LI Wei, YUAN Yunbin, OU Jikun, et al. A new global zenith tropospheric delay model IGGtrop for GNSS application[J]. China Science Bulletin, 2012, 57(15): 1317-1325. |
| [11] |
TORBEN S. The TropGrid2 standard tropospheric correction model[J]. GPS Solutions, 2014, 18(1): 123-131. DOI:10.1007/s10291-013-0316-x |
| [12] |
YAO Yibin, XU Chaoqian, SHI Junbo, et al. ITG: a new global GNSS tropospheric correction model[J]. Scientific Reports, 2015, 5: 10273. DOI:10.1038/srep10273 |
| [13] |
SUN Zhangyu, ZHANG Bao, YAO Yibin. A global model for estimating tropospheric delay and weighted mean temperature developed with atmospheric reanalysis data from 1979 to 2017[J]. Remote Sensing, 2019, 11(16): 1893. DOI:10.3390/rs11161893 |
| [14] |
MATEUS P, CATALO J, MENDES V B, et al. An ERA5-based hourly global pressure and temperature (HGPT) model[J]. Remote Sensing, 2020, 12(7): 1098. DOI:10.3390/rs12071098 |
| [15] |
URQUHART L, SANTOS M C, NIEVINSKI F G, et al. Generation and assessment of VMF1-Type grids using north-American numerical weather models[C]//Proceedings of 2011 IAG General Assembly. Melbourne, Australia: Springer, 2011.
|
| [16] |
LANDSKRON D, BOEHM J. VMF3/GPT3:refined discrete and empirical troposphere mapping functions[J]. Journal of Geodesy, 2018, 92(4): 349-360. DOI:10.1007/s00190-017-1066-2 |
| [17] |
ZUS F, DICK G, DOUSA J, et al. Systematic errors of mapping functions which are based on the VMF1 concept[J]. GPS Solutions, 2015, 19(2): 277-286. DOI:10.1007/s10291-014-0386-4 |
| [18] |
YU Xiaojing, ZHANG Lixia, ZHOU Tianjun, et al. The Asian subtropical westerly jet stream in CRA-40, ERA5, and CFSR reanalysis data: comparative assessment[J]. Journal of Meteorological Research, 2021, 35(1): 46-63. DOI:10.1007/s13351-021-0107-1 |
| [19] |
ZHAO Dan, ZHANG Lixia, ZHOU Tianjun, et al. Contributions of local and remote atmospheric moisture fluxes to east China precipitation estimated from CRA-40 reanalysis[J]. Journal of Meteorological Research, 2021, 35(1): 32-45. DOI:10.1007/s13351-021-0083-5 |
| [20] |
师春香. 多源融合网格实况数据与我国第一代全球大气再分析产品研发与应用进展[R]. 北京: 智慧地球大讲堂, 2021. SHI Chunxiang. Development and application of multi-source fusion grid reality data and the China's first generation global atmospheric reanalysis products[R]. Beijing: Smart Earth Lecture Hall, 2021. |
| [21] |
刘梦杰, 张卫星, 张镇驿, 等. CRA40在中国区域GNSS水汽反演中的适用性评估与分析[J]. 南京信息工程大学学报(自然科学版), 2021, 13(2): 138-144. LIU Mengjie, ZHANG Weixing, ZHANG Zhenyi, et al. On the applicability of CRA40 in GNSS precipitable water vapor retrieval over China[J]. Journal of Nanjing University of Information Science and Technology(Natural Science Edition), 2021, 13(2): 138-144. |
| [22] |
廖捷, 胡开喜, 江慧, 等. 全球大气再分析常规气象观测资料的预处理与同化应用[J]. 气象科技进展, 2018, 8(1): 133-142. LIAO Jie, HU Kaixi, JIANG Hui, et al. Pre-process and data selection for assimilation of conventional observations in the CMA global atmospheric reanalysis[J]. Advances in Meteorological Science and Technology, 2018, 8(1): 133-142. |
| [23] |
LIAO Jie, WANG Huiying, ZHOU Zijiang, et al. Integration, quality assurance, and usage of global aircraft observations in CRA[J]. Journal of Meteorological Research, 2021, 35(1): 1-16. DOI:10.1007/s13351-021-0093-3 |
| [24] |
YAO Bin, TENG Shiwen, LAI Ruize, et al. Can atmospheric reanalyses (CRA and ERA5) represent cloud spatiotemporal characteristics?[J]. Atmospheric Research, 2020, 244: 105091. DOI:10.1016/j.atmosres.2020.105091 |
| [25] |
LIANG Xiao, JIANG Lipeng, PAN Yang, et al. A 10-yr global land surface reanalysis interim dataset (CRA-Interim/Land): implementation and preliminary evaluation[J]. Journal of Meteorological Research, 2020, 34(1): 101-116. DOI:10.1007/s13351-020-9083-0 |
| [26] |
LI Chunxiang, ZHAO Tianbao, SHI Chunxiang, et al. Assessment of precipitation from the CRA40 dataset and new generation reanalysis datasets in the global domain[J]. International Journal of Climatology, 2021, 41(11): 5243-5263. DOI:10.1002/joc.7127 |
| [27] |
HERSBACH H, BELL B, BERRISFORD P, et al. The ERA5 global reanalysis[J]. Quarterly Journal of the Royal Meteorological Society, 2020, 146(730): 1999-2049. DOI:10.1002/qj.3803 |
| [28] |
HERSBACH H, BELL B, BERRISFORD P, et al. Global reanalysis: goodbye ERA-Interim, hello ERA5[J]. ECMWF newsletter, 2019(159): 17-24. |
| [29] |
DEE D P, UPPALA S M, SIMMONS A J, et al. The ERA-Interim reanalysis: configuration and performance of the data assimilation system[J]. Quarterly Journal of the Royal Meteorological Society, 2011, 137(656): 553-597. DOI:10.1002/qj.828 |
| [30] |
HOFMEISTER A. Determination of path delays in the atmosphere for geodetic VLBI by means of ray-tracing[D]. Vienna: Vienna University of Technology, 2016.
|
| [31] |
BOEHM J, SALSTEIN D, ALIZADEH M M, et al. Geodetic and atmospheric background[M]. Berlin: Springer, 2013: 1-33.
|
| [32] |
PAVLIS N K, HOLMES S A, KENYON S C, et al. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008)[J]. Journal of Geophysical Research: Solid Earth, 2012, 117(B4): B04406. |
| [33] |
WALLACE J M, HOBBS P V. Atmospheric thermodynamics[M]. San Diego: Elsevier, 2006: 63-111.
|
| [34] |
ROCKEN C, SOKOLOVSKIY S, JOHNSON J M, et al. Improved mapping of tropospheric delays[J]. Journal of Atmospheric and Oceanic Technology, 2001, 18(7): 1205-1213. |
| [35] |
NILSSON T, BOEHM J, WIJAYA D D, et al. Path delays in the neutral atmosphere[M]. Berlin: Springer, 2013: 73-136.
|
| [36] |
RVEGER J M. Refractive index formulae for radio waves[C]//Proceedings of 2002 FIG XXII international congress. Washington D.C., USA: FIG, 2002.
|
| [37] |
HOBIGER T, ICHIKAWA R, KONDO T, et al. Fast and accurate ray-tracing algorithms for real-time space geodetic applications using numerical weather models[J]. Journal of Geophysical Research: Atmospheres, 2008, 113(D20): 1-14. |
| [38] |
BOEHM J. Tropospheric delay in VLBI[D]. Vienna: Vienna University of Technology, 2004.
|
| [39] |
姚宜斌, 徐星宇, 胡羽丰. GGOS对流层延迟产品精度分析及在PPP中的应用[J]. 测绘学报, 2017, 46(3): 278-287. YAO Yibin, XU Xingyu, HU Yufeng. Precision analysis of GGOS tropospheric delay product and its application in PPP[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(3): 278-287. DOI:10.11947/j.AGCS.2017.20160383 |
| [40] |
张卫星. 中国区域融合地基GNSS等多种资料水汽反演、变化分析及应用[D]. 武汉: 武汉大学, 2016. ZHANG Weixing. Water vapor retrieval, variation analysis and applications over China using ground-based GNSS and multiple data[D]. Wuhan: Wuhan University, 2016. |
| [41] |
ZUMBERGE J F, HEFLIN M B, JEFFERSON D C, et al. Precise point positioning for the efficient and robust analysis of GPS data from large networks[J]. Journal of Geophysical Research Solid Earth, 1997, 102(B3): 5005-5017. |
| [42] |
ALSHAWAF F, ZUS F, BALIDAKIS K, et al. On the statistical significance of climatic trends estimated from GPS tropospheric time series[J]. Journal of Geophysical Research: Atmospheres, 2018, 123(19): 10967-10990. |
| [43] |
PACIONE R, ARASZKIEWICZ A, BROCKMANN E, et al. EPN-Repro2:a reference GNSS tropospheric data set over Europe[J]. Atmospheric Measurement Techniques, 2017, 10(5): 1689-1705. |
| [44] |
NIKOLAIDOU T, BALIDAKIS K, NIEVINSKI F, et al. Impact of different NWM-derived mapping functions on VLBI and GPS analysis[J]. Earth Planets and Space, 2018, 70(1): 95. |
| [45] |
FAN Haopeng, SUN Zhongmiao, ZHANG Liping, et al. A two-step estimation method of troposphere delay with consideration of mapping function errors[J]. Journal of Geodesy and Geoinformation Science, 2020, 3(1): 76-84. |



