2. 南京邮电大学江苏省智慧健康大数据分析与位置服务工程实验室, 江苏 南京 210023;
3. 南京师范大学地理科学学院, 江苏 南京 210023
2. Smart Health Big Data Analysis and Location Services Engineering Research Center of Jiangsu Province, Nanjing University of Posts and Telecommunications, Nanjing 210023, China;
3. School of Geographic Sciences, Nanjing Normal University, Nanjing 210023, China
空间优化是实现空间要素资源合理利用的重要途径,是地理信息科学的重要研究方向之一,旨在实现空间约束条件下地理决策问题的最优解计算[1],已广泛应用于土地利用配置[2]、地理模拟优化[3]、交通布局配置[4]、设施配置空间优化[5]等领域。设施配置空间优化是空间优化问题的典型范例,以计算研究区内多个设施的地理位置、容量为结果,以提升地理空间布局结构合理性为目标。根据设施分布连续程度分类,设施配置空间优化分为离散设施空间优化、连续设施空间优化;根据关键构成分类,可分为3个部分:目标函数、约束条件及优化方法[6];根据目标函数和约束条件差异性,又可形成多种设施配置模型,如:P中值模型、P中心模型、覆盖模型、动态选址模型、多目标模型、网络中心模型等[7],各模型本质仍为设施资源、需求者、服务质量三者的博弈平衡。
设施配置空间优化指为基于数学规划方法实现设施布局和调度,以提升居民日常生活所需各类公共产品和服务获得的便利性,属于典型的NP-Hard问题,面临决策环境综合、问题规范描述复杂、空间结构交错、问题规模对搜索解质量有显著抑制效应等挑战[6]。设施配置空间优化已被证明为不存在经典多项式时间算法的问题,此类问题求解容易导致组合爆炸[6]。为应对设施配置空间优化问题计算挑战,诸多研究从精确方法和启发式方法两方面开展[5]。精确方法如位置分配模型[8]、二次规划[9]等,具备结构清晰且求解问题简单的特征[10];而启发式方法是基于经验法则、策略和进化过程的系列算法,包括模拟退火[11]、群智能算法[12]、多目标改进免疫算法[13]、蚁群优化算法[14]等,具有仿生启发搜索的特征。然而,随着设施规模增加,设施配置空间优化问题的解空间呈现“高维多峰”组合爆炸,促使求解过程易陷入局部搜索,如:从城市内1000个候选位置中选中100个,建设0至10区间容量的公共充电站,空间计算规模为C1000100×10100,而当选中200个时空间计算规模“爆炸”为C1000200×10200,可见设施规模对计算复杂度的直接影响。学者们从变种混合革新、计算框架更新视角出发,对设施配置启发式方法进行改进,形成如差分进化混合粒子群算法、并行遗传算法以缓解设施规模对计算复杂度影响,并取得了成效[15]。然而,传统设施配置启发式方法及其改进仍遵循基于确定性编码逻辑的连续空间渐进式搜索策略,多以理论场景为分析对象,难以适应城市耦合环境下地理现象空间相关性和空间异质性[16]混合交替的条件约束。从而在大规模城市设施配置空间优化应用场景中,传统设施配置启发式方法及其改进仍会趋近难以“逃逸”局部搜索,求解质量待提升。因此,如何适应城市耦合环境下地理现象相关性和异质性约束,设计出一种编码表达状态更多、种群更新搜索尺度更大的设施配置启发式方法,亟待研究和突破。
2020年美国国家地理空间情报局指出需发展地理空间优化量子计算方法,以求解复杂的、多变量的地理空间优化问题。类比于模拟退火算法翻越过“山峰”过程易陷入局部而无法逃逸“山谷”,日本学者西森秀稔吸纳量子力学中的量子隧穿效应理论,提出“山峰”可以“穿过”的量子退火算法,为量子退火计算机提供理论基础[17]。本文借鉴量子计算思想渊源[18],提出应用量子进化机制构建设施配置启发式算法科学假设,以适用于城市耦合环境下地理现象相关性和异质性约束,实现设施配置搜索解质量提升。量子进化机制是实现高性能、高质量计算的重要方向,已于硬件和算法层面论证,如量子遗传算法[19]、量子进化算法[20-21]、量子密码算法[22]、量子搜索算法[23]。近年来,结合量子进化机制的新型智能算法包括:量子人工神经网络、量子的模式识别算法、量子衍生进化算法、量子的聚类算法、量子退火算法、量子小波与小波包算法[24]等。综上所述,针对如何设计出符合离散型设施配置空间优化的量子进化算法,本文首先于第1节阐述设施配置空间优化基本流程,然后在第2节和第3节对量子计算特性和量子进化算法设计流程进行剖析,最后于第4节和第5节进行试验验证和总结。
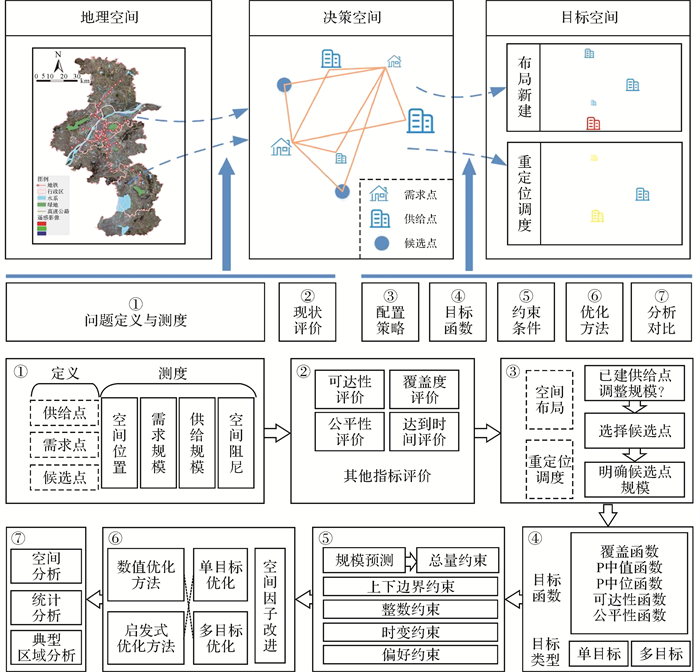
1 设施配置空间优化流程从概念设计视角,设施配置空间优化过程可看作3种空间域的转换,即:地理空间域、决策空间域和目标空间域(图 1),适用于各种设施,包括:教育、文体、卫生、商业、饮食、服务和行政经济管理等。地理空间域是指居民日常生活的物理空间,涉及居民区、已建离散设施及已建交通路网条件等。决策空间域是指通过对地理空间问题定义和测度而得到的求解空间,其中居民区抽象为需求点,已建离散设施抽象为已建供给点,并根据实际城市规划条件、宜建、禁建条件而形成的待建候选点集合。目标空间域包括设施空间布局配置(layout allocation)及空间重定位(relocation),前者以规划新建设施位置和规模为目标,后者以对已建服务设施进行资源重新调度为目标。参照文献[25]中的管理决策分析对决策分析框架的定义,决策分析包括:识别问题、设计目标、拟订方案、评价分析、优化方案、实施反馈。本文总结并形成设施配置空间优化框架流程的7个环节(图 1):①问题定义与测度;②现状评价;③目标函数;④空间配置类型;⑤约束条件;⑥优化算法;⑦分析对比。从地理空间域到决策空间域是一个测度和范化的过程,依赖于环节①和环节②;从决策空间域到目标空间域是一个优化求解的过程,依赖于环节③—环节⑦。因环节不同,设施配置空间优化框架可组合成多种研究问题,本文聚焦研究有容量约束的离散型设施组合配置问题。
|
| 图 1 种空间转换关系及设施配置流程 Fig. 1 Schematic diagram of three domains transformational relation and the flowchart of facility allocation |
2 量子计算特性与算法结构
量子计算具有并行性、状态叠加性等特性,在组合优化问题中具有显著优势,因此,在设施配置空间优化问题中引入量子计算机制,是突破高维多峰空间优化问题的全新途径。基于量子计算原理而模拟设计出的优化算法结构称为量子进化算法,包括基于量子物理学的搜索算法和基于量子计算与传统智能优化算法结合形成的量子衍生智能算法。量子衍生智能算法实现了量子原理与智能计算的结合,利用量子并行计算等特性弥补了传统智能算法的某些不足,如:传统智能算法搜索速度慢、易出现早熟现象,主要算法涉及量子退火算法、量子进化算法、量子神经网络、量子贝叶斯网络、量子小波变换、量子聚类算法等[17]。这些算法的共同点是应用了量子计算机制或启发机制,符合量子力学行为特征,延续了量子计算优势。受限于量子计算机硬件发展,这些算法目前主要通过模拟量子计算实现,但它们较传统智能算法仍具有显著优势。
2.1 量子计算特性量子计算特性概括为状态叠加性、状态相干性、量子并行性、状态纠缠性[18]。这些特性的形成来源于量子比特、量子概率幅观测及量子门更新。与经典比特不同,量子比特(Qubit)可记录量子位的概率幅,可同时存储和表达“0”和“1”两种状态,可表示为|ψ〉=α|0〉+β|1〉,α、β是两个复常数,称为量子比特概率幅,满足|α|2+|β|2=1,|0〉和|1〉分别表示“0”和“1”两种状态,形成状态叠加性。状态相干性体现在基态|0〉的概率幅,由于量子门作用得到增加,同时|1〉的概率幅度降低,对在基态的线性叠加状态下的量子系统|ϕi〉是相干的,当周围的环境作用于该系统时,所处的叠加状态不再存在,并按照|pi|2坍塌到某一个唯一的基态|ϕi〉。量子并行性体现在一旦量子门对空间中的量子状态进行操作,其中所有的基态都会受到影响。状态纠缠性体现在当两个子系统中存在的一些状态并相互作用时,状态会同时被修改。
2.2 经典量子进化算法结构文献[26—27]总结了经典量子进化算法流程,算法流程见算子1。该算法流程含7个步骤,主要涉及量子比特编码算子、适应度评价、概率坍塌算子、量子门更新算子、精英策略等。
算子1:传统量子进化算法流程
输入:设定迭代开始条件
输出:最后代数种群的个体
量子种群初始化Q(t),令迭代次数t←0,根据量子比特编码算子初始化量子种群Q(t);
while t < N do
量子染色体坍塌观测,通过概率坍塌算子,确定每个量子染色体的解,得到解种群P(t);
对解种群P(t)进行适应度评价,根据目标函数,来评价P(t)中每个解个体的适应度。其中,目标函数应实际应用问题而定义;
精英策略选择,从P(t)中选择最好的解,并保持到精英种群B(t)中;
利用量子门U(Δθ)算子更新形成新一代量子种群Q(t+1),使用量子门U(Δθ)更新机制计算得到新一代量子种群Q(t+1),详见量子门U(Δθ)算子;
对新一代量子种群Q(t+1)补充精英个体,从B(t-1)选择出最好量子染色体,并存储至新一代量子种群Q(t+1);
t←t+1;
end
3 面向设施配置空间优化的量子进化算法经典量子进化算法在理论连续函数上已被证明可用、高质量,但集成至设施配置空间优化问题中,面临着结合难的挑战。究其原因,经典量子进化算法使用二进制量子染色体编码,是将量子状态又重新随机地转换为经典比特状态。这种观测、编码方式在实际应用问题求解中具有一定局限性,尤其是总量约束的整数组合优化问题[25],如在|0〉和|1〉的叠加态的染色体中会导致染色体不稳定,存在“长度灾”,且不适应于条件约束问题,如总规模约束、整数约束等。已有研究针对经典量子进化算法的“长度灾”提出基于实数编码的量子进化算法[26-30],此类算法在迭代过程中,首先改进编码和解码过程,从而提高了求解效率;然后改善|0〉和|1〉的叠加态编码带来的精度丢失不足;最后,改善因求解问题维度变大引起的“长度灾”。
本文以有容量约束的离散型服务设施选址为设施配置基础模型,目标函数R(t)可为最小化/最大化代价函数(例如:最小化通行时间、最大化公平性),讨论并设计基于实数编码的量子进化算法,提出面向设施配置空间优化的量子进化算法(quantum evolutionary algorithm for spatial optimization of facility allocation, QEA-SOFA),流程如图 2所示,主框架与经典量子进化算法[24-25]保持一致,包含“种群生成-种群进化-种群评价”,在编码结构、量子变异、离散交叉等算子上改进。

|
| 图 2 QEA-SOFA算法流程 Fig. 2 Flowchart of QEA-SOFA algorithm |
3.1 四倍体量子染色体编码算子
量子编码方式改进是量子进化算法设计的研究重点。在吸纳已有研究思想基础上[25-27],本文提出一种四倍体量子染色体编码方式,染色体同时记录数值、两种量子比特态、是否更新标记状态量。四倍体量子染色体编码避免烦琐的编码和解码过程,提升了个体信息的保持,适用于存在条件约束的设施配置空间优化问题,其优势在于染色体长度大幅缩短、进化效率提升、量子比特通过量子逻辑门算子更新旋转得到更多样化的候选解。四倍体量子编码染色体qrt较之前研究中的三倍体量子编码染色体[30]加入了无效变异标记符gjt,其初始值均为0,记录量子变异的有效性次数,用于控制个体的量子变异循环停止条件。四倍体量子染色体编码的编解码方案为
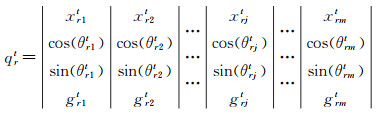 (1)
(1)
式中,qrt可以简化成传统的量子概率幅表示形式
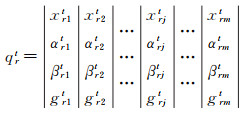 (2)
(2)
式中,αrjt和βrjt满足归一化条件,|αrjt|2+|βrjt|2=1, j=1, 2, …, m。在城市设施配置空间优化问题中,m为供给点数量,每个xrjt变量表示在第t代中第r个供给点的供给规模,且xrjt∈[BOTTOM, UP]。
式中,关于三角变换初始角度的确立,采用如下方式
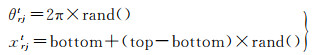 (3)
(3)
式中,rand( )函数为(0, 1)之间的随机数;i表示种族规模,i=1, 2, …, m;j表示量子位,j=1, 2, …, n。
3.2 总量约束算子总量约束算子可实现设施配置容量限制,属于染色体的一种修补机制。其基于四倍体量子染色体编码,在调整单个个体容量的同时,增加同步调整逻辑,完成对βrjt、αrjt的调整,形成传导过程。总量约束算子主体分为个体初始化、初步调平和精细调平3部分,具体约束流程如算子2所示。总量约束算子对[xrjt, arjt, βrjt]T均实现了调节,不同的策略在于xrjt实现了精细调平约束,使之所有之和完全符合总量约束值E_setting,而对arjt、βrjt实现了初步调平,使之与xrjt值基本保持同步。
算子2: 四倍体量子整数编码染色体总量约束算子
输入:上限UP,下限BOTTOM,染色体维度M,总量约束值E_setting,四倍体量子染色体
输出:总量约束后的染色体qrt
对qrt的[xtr1, xtr2, …, xrjt, …, xrMt]求和,得到SUM
初步调平,采用广播机制更新每个xrjt的值,更新方式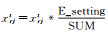
初步调平,采用广播机制更新每个αrjt的值,更新方式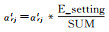
初步调平,用广播机制更新每个αrjt的值,更新方式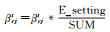
精细调平:
If sum([xr1t, xr2t, …, xrjt, …, xrMt])!=E_setting then
While Δ!=0 do
随机选取个体qrt的基因位置u,u∈[1, M]
If Δ>0 then
xrut=xrut-1
Δ+=1
end
else if Δ < 0 then
xrut=xrut+1
Δ+=1
end
else Δ==0
Break
end
end
end
3.3 量子变异算子量子变异算子设计旨在模拟量子坍塌观测操作,本文直接采用三角函数变换更新模拟观测。在设计量子变异算子时,QEA-SOFA算法采用多点变异,但多点数量不宜过大,过大会导致染色体稳定性被破坏,从而失去进化价值。当QEA-SOFA算法运行到第t代时,群体为P(t)={q1t, q2t, …, qrt, …, qLt},L为群体规模,对于第r个染色体个体qrt,从中选取多个基因位开展量子变异,选取方式为产生随机整数方式。以其中1个基因位为例,第j个基因位[xrjt, αrjt, βrjt, grjt]T,对实数变量xrjt进行高斯变异,得到xrjt+1,其变异计算方式如下
 (4)
(4)
式中:*从(α, β)取值,N(0, (σrjt*)2)是均值为0方差为(σrjt*)2的高斯分布值,且(σrjt*)2为
 (5)
(5)
由式(4)和式(5)生成的xrjt+1值,有较大概率超出了[BOTTOM, UP]的范围,此时需要做单个基因位的越界控制(等价于单个服务设施容量的限制),控制逻辑如算子3所示。
算子3: 越界控制算子片段
输入:xrjt+1
输出:xrjt+1
If xrjt+1>UP then
xrjt+1=2*UP-xrjt+1
end
If xrjt+1 < BOTTOM then
xrjt+1=2*bottom-xrjt+1
end
完成个体多基因位量子变异后,调取总量约束算子计算,得到第r个染色体个体qrt的变异染色体qrt+1,并计算变异染色体qrt+1适应度,如果其适应度优于qrt,则认为该变异为有效进化;否则为无效进化,无效进化处理步骤如下:需要更新无效变异标记符行grjt,自增1;执行量子概率幅更新U旋转门(式(6)),更新βrjt、αrjt;抛弃现有的qrt+1,重新采用多点高斯变异,生成新的qrt+1。这3个步骤的循环停止条件有两种:一是达成有效进化,更新grjt为0,且终止对qrt的量子变异,然后处理下一个个体;二是grjt值大于或等于有效进化次数Num_Eva设置值(如设置Num_Eva为5),终止循环,并进入更大尺度βrjt、αrjt搜索,更新βrjt、αrjt值。以下将对量子概率幅更新U旋转门详细阐述。
量子概率幅更新U旋转门算子,以更新[αrjt βrjt]T的值[30],得到[αrjt+1 βrjt+1]T为计算目的,计算公式如下
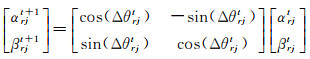 (6)
(6)
式中,Δθrjt为量子旋转门旋转角,其计算方式包含两种[31-34],分别为固定进化尺度方式和梯度进化尺度方式。
固定进化尺度方式的Δθrjt计算公式如下
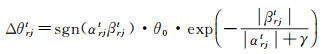 (7)
(7)
梯度进化尺度方式的Δθrjt计算公式如下
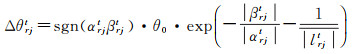 (8)
(8)
式中,sgn(·)为符号函数,若内部值αrjtβrjt为正,则符号函数为正,反之为负,该符号函数用于控制旋转角方向;|βrjt|、|αrjt|分别为βrjt、αrjt的绝对值;θ0为初始旋转角,可在执行QEA-SOFA算法时设为定值,如设为0.1π;γ为进化尺度,可在执行QEA-SOFA算法时设为定值,如设为0.05;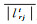
2种方式的计算结构、变量内涵保持一致,不同之处在于进化尺度部分的确立方式。
3.4 量子交叉算子量子变异算子实现个体内部的基因位信息更新,但未能实现个体之间信息交互,因此需引入量子交叉算子。QEA-SOFA算法中的量子交叉算子采用离散交叉模式,迭代一定代数τc之后,实施一次四倍体量子染色体之间的交叉操作,具体交叉方式如下:首先,对种群P(t)={q1t, q2t, …, qrt, …, qLt}评价适应度,得到适应度集合R(t);然后,对R(t)进行适应度排序,选取一定数量的、排名靠前的优秀个体,作为临时父代;最后,从临时父代中随机抽取qut和qvt,实施多点交叉,交换被随机抽取的多点基因位的值,得到交叉后的新个体qut+1和qvt+1。
4 试验与应用从理论和应用两个层面,证明QEA-SOFA算法的有效性、用益性,包括试验1(理论函数试验)、试验2(应用试验)。其中,试验1以Ackley和Griewank标准测试函数求解为研究情景,试验2以南京市急救服务设施配置空间重定位优化为应用情景。
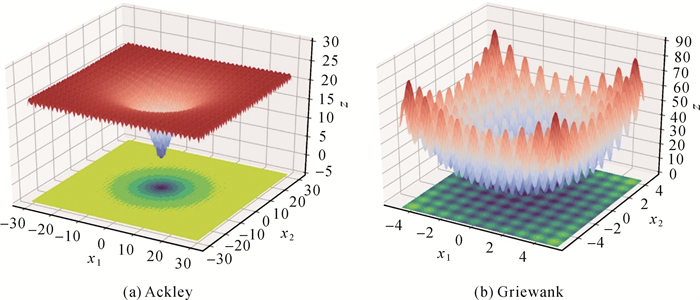
4.1 试验1:QEA-SOFA算法在理论高维多峰函数上求解(1) 函数与参数设置。为考察QEA-SOFA算法在理论高维多峰函数(high-dimensional multimodal function)上求解有效性,本文选取实数编码遗传算法(real-coding genetic algorithm,RCGA)[29]为对照组,并以Ackley和Griewank函数为标准测试函数,优化目标为求解全局最小值。图 3为Ackley和Griewank函数2维曲面图,可知Ackley和Griewank函数具有典型“多峰”结构特征。Ackley和Griewank函数维度设定为100维,且存在上下边界,2个测试函数的理论最优值均为0(表 1)。QEA-SOFA算法与RCGA算法参数设置一致,变异概率设置为0.05,交叉概率为0.66,种群规模为200个,进化代数为2000代,染色体长度为100;QEA-SOFA算法的特有参数设置,变化幅度初始值θ0=0.4×π,学习率设置为0.05。试验分2组对比场景,场景1是无约束条件场景,场景2是有约束条件场景(具体约束条件为总量约束和整数编码约束,Ackley函数的总量约束参数E_setting设置为500,上边界UP设置为10,下边界BOTTOM设置为1;Griewank函数的总量约束参数设置为1000,上边界UP设置为50,下边界BOTTOM设置为1)。
|
| 图 3 高维多峰测试函数2维可视化 Fig. 3 2D visualization of high-dimensional multi-peak test function |
| 函数名称 | 测试函数公式 | 上下边界 | 理论最优值 | 解维度 |
| Ackley | 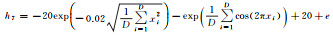 |
(-30, 30) | 0 | 100 |
| Griewank | 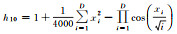 |
(-600, 600) | 0 | 100 |
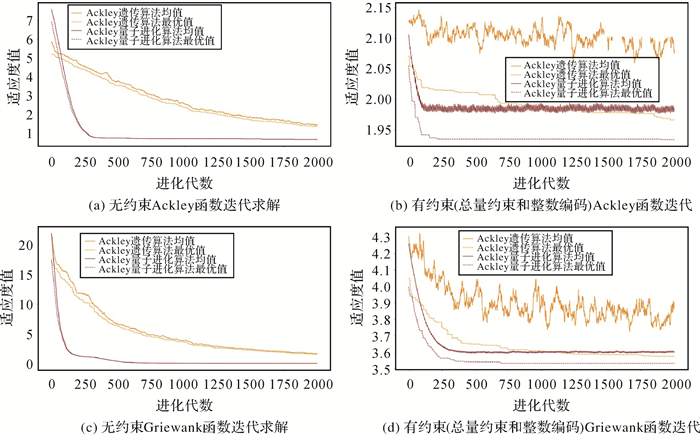
(2) 算法对比结果。采用Ackley和Griewank函数的各代目标均值(average value)和最优值(best value) 作为评价QEA-SOFA算法和RCGA算法搜索解的质量指标,场景1和场景2的迭代收敛过程如图 4所示。场景1中(图 4(a)、(c)),QEA-SOFA算法在Ackley、Griewank函数上的搜索解适应度明显优于RCGA算法的搜索解适应度,且其代际间收敛速度更快,于250代左右已接近最优值,而RCGA算法于2000代时的最优值仍劣于QEA-SOFA算法结果。场景2中(图 4(b)、(d)),当对RCGA算法增加总量约束和整数编码后,其求解过程中各代均值呈现显著波动变化,收敛缓慢;而QEA-SOFA算法求解过程呈现“快速下降,然后低频波动”变化。这也说明QEA-SOFA算法在增加约束条件后仍保持相对更稳定的搜索特性,该特性取决于量子变异机制的多态表达。综述,QEA-SOFA算法较RCGA算法而言,具有显著解质量增强效用。
|
| 图 4 收敛过程对比 Fig. 4 Convergence process comparison |
4.2 试验2:QEA-SOFA算法在设施配置中的应用
为验证QEA-SOFA算法在设施配置空间优化问题的价值,试验2以南京市为研究区,以急救站设施空间重定位[35]为研究问题。南京市位于长江下游中部地区,是国家区域中心城市、特大城市,常住人口850万人,综合医疗资源丰富,公立医院241所、急救站65个。目前,南京院前急救反应时间远大于国家标准,南京市急救平均反应时间为16 min (http://jiangsu.sina.com.cn/news/s/2018-01-31/detail-ifyqyuhy8000404.shtml),尚未达到国家标准要求,且急救反应时间20 min以上的占比过高。研究区内各急救站的救护车资源配置与区域人口分布、交通条件仍存在不协同的矛盾,呈现出“富集、贫瘠”公平性差异大的情景。因此,综合人口、交通和医疗服务的典型性,本文以特大城市南京作为研究区。人口分布数据为基于手机信令的人口空间分布值,交通数据为高德地图API实时导航路径数据,研究单元为街区单元数据。研究问题凝练为“如何在已有65个急救站上,通过对169辆救护车空间重定位配置,优化公平性目标,实现公平性目标函数的最大化”,目标函数为急救服务设施可达性的公平性函数。公平性函数是以可达性模型作为基础,以各居民点到设施的公平性差异性的倒数最大化为目标的设施配置空间优化模型[36],实现了设施配置不一致性的评价,目标函数的详细定义参考文献[36]。此外,结合优化算法参数默认设置和研究区实际急救站资源配置上下限(BOTTOM、UP),确立面向急救设施配置应用试验的参数设置,见表 2。
| 序号 | 参数名称 | 取值 | 备注 |
| 1 | MP | 0.5 | 变异概率 |
| 2 | CP | 0.8 | 交叉概率 |
| 3 | POPSIZE | 20 | 种群规模 |
| 4 | GENERATIONS | 200 | 迭代次数 |
| 5 | θ0 | 0.1π | 初始旋转角 |
| 6 | γ | 0.9 | 进化尺度 |
| 7 | BOTTOM | 0 | 急救站拥有最少救护车数 |
| 8 | UP | 10 | 急救站拥有最多救护车数 |
| 9 | τc | 5 | 离散交叉 |
| 10 | INVALID_ MUTATION_T | 10 | 无效变异循环代数阈值 |
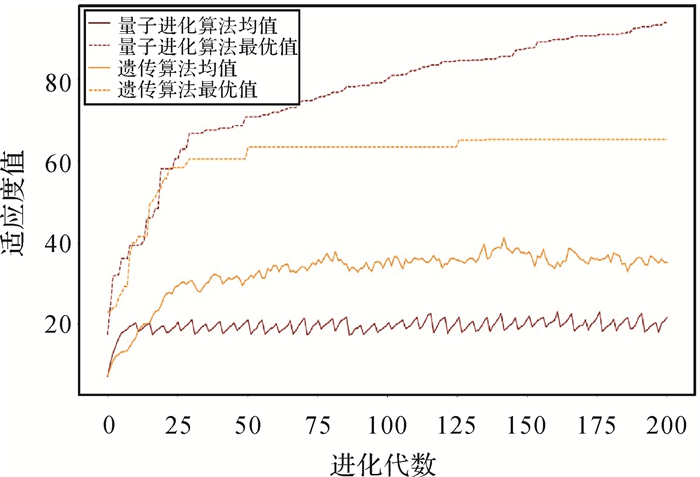
开展急救服务设施配置试验,求解公平性最大化适应度值,得迭代收敛图(图 5)。QEA-SOFA算法与RCGA算法均呈现收敛增大趋势,两者平均适应度呈现“先上升后震荡”,最大适应度呈现“先上升后稳定”收敛趋势,说明两者对空间优化均奏效。但QEA-SOFA算法在适应度质量和代际进化速度上明显优于RCGA算法,QEA-SOFA算法的平均适应度在迭代次数为5时趋于震荡,而RCGA算法的平均适应度在迭代次数为125时才停止增长,趋于平缓。QEA-SOFA算法在搜索解适应度上明显优于RCGA算法,QEA-SOFA算法的最大适应度值趋近100,而RCGA算法的最大适应度值趋于60,相对质量提升约66%。以上结果说明QEA-SOFA算法在急救服务设施配置求解中搜索能力更强,改善了高维多峰优化容易陷入局部搜索的不足。为表征两种算法对不同站点配置结果带来的差异性,本文构建急救设施配置结果对比表(表 3)。由表 3列Ⅲ可知,优化前急救资源集中分布在鼓楼区、秦淮区;由表 3列Ⅳ和Ⅴ可知,优化后配置结果更倾向于将资源调度至建邺区、雨花台区及周边近郊区调度。推测成因,建邺区、雨花台区及周边近郊区居住人口密集,产业聚集,需求量较大,人均急救资源较低,所以呈现需求增长的趋势。优化结果与人口规模成正比关系,说明RCGA算法和QEA-SOFA算法可根据人口、交通可达性条件调度设施,以改善资源“富集、贫瘠”公平性差异。此外,选取位于典型区域的站点,如:浦口大学城区域(ID为:P14、P22、P23、P26、P28、P29、P30、P31)、江宁大学城区域(ID为:P47、P49、P50、P51、P53、P55),发现RCGA算法提高了浦口大学城区域的急救资源量,以P22、P23急救站最典型,而QEA-SOFA算法提高了江宁区大学城区域的急救资源量,以P49、P50、P51、P55急救站为典型。结合田野调查法,江宁大学城拥有17所高校,在校生约25万人,周边居民及园区人口密集;浦口大学城入驻高校7所,在校生约10万人,周边居民及园区人口相对稀疏。该人口分布差异间接说明江宁大学城及其周边范围对潜在急救资源需求量更大,应当提升江宁大学城区域的急救资源配置量。对比典型区域的规模、人口、资源配置量,发现QEA-SOFA算法结果更符合田野调查结果。从人口空间分布视角,该结果也论证了QEA-SOFA算法对典型空间异质区域的局部搜索具有更优精度,说明QEA-SOFA算法在局部高维多峰区域的搜索能力更强。
|
| 图 5 QEA-SOFA算法与RCGA算法试验结果对比 Fig. 5 Comparison diagram of experimental results between QEA-SOFA algorithm and RCGA algorithm |
| ID | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | ID | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | |
| P01 | 梅山医院分站 | 118.63°E, 31.9°N | 5 | 9 | 3 | P34 | 六合医院竹镇站 | 118.69°E, 32.52°N | 1 | 0 | 1 | |
| P02 | 岱山社区分站 | 118.7°E, 31.95°N | 4 | 8 | 3 | P35 | 六合医院东沟站 | 118.85°E, 32.35°N | 1 | 2 | 0 | |
| P03 | 中西结合医院站 | 118.86°E, 32.04°N | 2 | 4 | 1 | P36 | 六合中医院分站 | 118.85°E, 32.32°N | 2 | 0 | 0 | |
| P04 | 邦德骨科医院站 | 118.81°E, 32.05°N | 2 | 0 | 2 | P37 | 溧水医院石湫站 | 118.92°E, 31.63°N | 1 | 3 | 1 | |
| P05 | 市儿童医院站 | 118.79°E, 32.06°N | 2 | 2 | 3 | P38 | 溧水医院东屏站 | 119.12°E, 31.71°N | 2 | 2 | 1 | |
| P06 | 省中医院站 | 118.78°E, 32.05°N | 3 | 3 | 6 | P39 | 溧水中医院分站 | 119.03°E, 31.66°N | 2 | 1 | 0 | |
| P07 | 省中西结合医院站 | 118.82°E, 32.11°N | 2 | 6 | 0 | P40 | 溧水中医院和凤站 | 119.01°E, 31.49°N | 2 | 0 | 0 | |
| P08 | 龙潭社区中心站 | 119.06°E, 32.17°N | 4 | 4 | 4 | P41 | 溧水医院白马站 | 119.19°E, 31.58°N | 1 | 1 | 1 | |
| P09 | 栖霞区医院分站 | 118.96°E, 32.15°N | 4 | 1 | 3 | P42 | 溧水人民医院分站 | 119.04°E, 31.64°N | 2 | 2 | 2 | |
| P10 | 瑞东医院站 | 118.94°E, 32.16°N | 4 | 9 | 2 | P43 | 江心洲社区中心站 | 118.7°E, 32.02°N | 2 | 2 | 0 | |
| P11 | 八卦洲社区分站 | 118.83°E, 32.18°N | 3 | 2 | 2 | P44 | 明基医院分站 | 118.74°E, 31.99°N | 3 | 6 | 7 | |
| P12 | 市红十字医院站 | 118.8°E, 32.03°N | 9 | 10 | 0 | P45 | 省第二中医院分站 | 118.76°E, 32.03°N | 2 | 5 | 3 | |
| P13 | 市中医院站 | 118.8°E, 32.03°N | 10 | 4 | 10 | P46 | 双闸社区中心分站 | 118.71°E, 31.99°N | 3 | 5 | 5 | |
| P14 | 医大四附院泰山站 | 118.72°E, 32.15°N | 2 | 1 | 3 | P47 | 江宁中医医院分站 | 118.86°E, 31.97°N | 3 | 0 | 3 | |
| P15 | 浦口中医院站 | 118.64°E, 32.07°N | 2 | 3 | 0 | P48 | 江宁医院禄口站 | 118.86°E, 31.78°N | 3 | 1 | 2 | |
| P16 | 浦口中心医院站 | 118.64°E, 32.06°N | 2 | 5 | 3 | P49 | 江宁医院分站 | 118.86°E, 31.96°N | 3 | 4 | 8 | |
| P17 | 浦口中心医院桥林站 | 118.54°E, 31.94°N | 1 | 2 | 4 | P50 | 江宁医院开发区站 | 118.81°E, 31.94°N | 3 | 1 | 9 | |
| P18 | 浦口中心医院星甸站 | 118.45°E, 32.03°N | 1 | 3 | 1 | P51 | 江宁医院湖山路站 | 118.88°E, 31.96°N | 2 | 5 | 9 | |
| P19 | 浦口中医院永宁站 | 118.58°E, 32.14°N | 2 | 2 | 3 | P52 | 江宁医院湖熟站 | 118.99°E, 31.86°N | 1 | 6 | 3 | |
| P20 | 浦口中医院汤泉站 | 118.52°E, 32.1°N | 2 | 3 | 2 | P53 | 同仁医院分站 | 118.8°E, 31.92°N | 3 | 0 | 4 | |
| P21 | 南医大四附院站 | 118.73°E, 32.11°N | 2 | 1 | 2 | P54 | 同仁医院横溪站 | 118.78°E, 31.72°N | 3 | 2 | 4 | |
| P22 | 南医大四附院盘城站 | 118.72°E, 32.21°N | 2 | 8 | 1 | P55 | 逸夫医院分站 | 118.9°E, 31.94°N | 3 | 0 | 10 | |
| P23 | 高新医院分站 | 118.72°E, 32.18°N | 2 | 6 | 3 | P56 | 江宁医院土桥站 | 119.06°E, 31.94°N | 3 | 1 | 1 | |
| P24 | 六合人民医院程桥站 | 118.73°E, 32.39°N | 1 | 2 | 0 | P57 | 市第二医院分站 | 118.78°E, 32.09°N | 11 | 7 | 10 | |
| P25 | 六合人民医院横梁站 | 118.94°E, 32.33°N | 1 | 2 | 1 | P58 | 医大二院萨家湾站 | 118.76°E, 32.09°N | 10 | 1 | 10 | |
| P26 | 扬子医院分站 | 118.78°E, 32.25°N | 2 | 1 | 2 | P59 | 高淳人民医院站 | 118.88°E, 31.33°N | 2 | 1 | 0 | |
| P27 | 六合人民医院马集站 | 118.82°E, 32.54°N | 1 | 0 | 0 | P60 | 高淳医院砖墙站 | 118.84°E, 31.27°N | 1 | 0 | 0 | |
| P28 | 南医大四附院沿江站 | 118.73°E, 32.17°N | 2 | 1 | 2 | P61 | 高淳医院桠溪站 | 119.17°E, 31.37°N | 1 | 0 | 0 | |
| P29 | 南钢医院分站 | 118.75°E, 32.21°N | 2 | 2 | 4 | P62 | 高淳医院东坝站 | 119.07°E, 31.31°N | 1 | 1 | 1 | |
| P30 | 江北人民医院分站 | 118.76°E, 32.24°N | 2 | 1 | 0 | P63 | 高淳医院阳江站 | 118.83°E, 31.34°N | 1 | 1 | 1 | |
| P31 | 中大江北院区站 | 118.75°E, 32.23°N | 2 | 1 | 2 | P64 | 高淳医院固城站 | 118.98°E, 31.32°N | 1 | 0 | 0 | |
| P32 | 六合人民医院站 | 118.85°E, 32.35°N | 2 | 3 | 3 | P65 | 高淳中医院分站 | 118.9°E, 31.35°N | 2 | 0 | 2 | |
| P33 | 六合医院金牛湖站 | 118.94°E, 32.42°N | 1 | 0 | 2 | |||||||
| 注:列Ⅰ为急救站名称,列Ⅱ为经纬度坐标,列Ⅲ为优化前数量(辆),列Ⅳ为RCGA优化后数量(辆),列Ⅴ为QEA-SOFA优化后数量(辆)。P01—P02属于雨花台区,P03—P07属于玄武区,P08—P11属于栖霞区,P12—P13属于秦淮区,P14—P23属于浦口区,P24—P36属于六合区,P37—P42属于溧水区,P43—P46属于建邺区,P47—P56属于江宁区,P57—P8属于鼓楼区,P59—P65属于高淳区。与表 3相配套的空间配置成果图参见https://doi.org/10.6084/m9.figshare.19071482.v1。 | ||||||||||||
4.3 算法时间复杂度分析
QEA-SOFA算法和RCGA算法的框架一致,遵循“种群生成-种群重组-个体评估”的进化范式,且均属于基于种群的智能进化算法((μ+λ)EA)范畴[37]。(μ+λ)EA理论研究包括收敛性分析和时间复杂性分析,其中,时间复杂度分析利于证明机制和效率根本问题。受限于(μ+λ)EA的重组、变异算子的随机性本质,(μ+λ)EA时间复杂性分析极其困难,仍以描述算法基本操作数量为准,也可用目标函数评估次数或者迭代次数评估,而忽略每一次迭代中交叉、变异、选择等进化算子所耗费的时间。然而在实际应用场景中,(μ+λ)EA计算时间主要耗费于个体目标函数评估和约束条件上,目标函数的结构复杂性和约束条件的边界清晰性会对耗时产生巨大的影响。同理,QEA-SOFA算法设计中时间复杂度也受到了目标函数评估和约束条件的影响。由于QEA-SOFA算法量子变异算子中包含着个体量子变异后循环判断是否为有效变异的操作,使得单个个体目标函数评估时间复杂度在理论最坏条件下,由QEA-SOFA算法的O(1)发展为O(logNum_EvaN)。因此,顾及个体遵循“随机生成-约束条件-目标函数评价”基本步骤,约束条件(总量约束算子)时间复杂度也遵循相同机制。但QEA-SOFA算法在代际量子变异次数和量子交叉次数上具有设计优势,其中,代际量子交叉时间复杂度在理论最差条件下为O(logτN),而RCGA算法为O(N)。因此,QEA-SOFA算法和RCGA算法在理论时间复杂度上各有优劣、相互博弈,且会受求解问题目标函数和约束条件复杂性影响。当QEA-SOFA算法作用于无约束场景的高维多峰函数求解问题时,最优解形成的耗时与RCGA算法相近,且因目标函数不同而有差异;当引入约束条件后,两者耗时均增大;当应用于设施配置应用问题时,顾及设施配置公平性函数是一种典型的、结构复杂的空间相互作用函数,使得QEA-SOFA算法求解的总迭代耗时和最优解形成耗时均扩大。该现象与文献[38]研究成果结论保持一致,即量子优化的时间加速成效在现有模拟量子计算中仍有限,受限于量子机制频繁模拟转化。但QEA-SOFA算法的最优解质量优于RCGA算法,尤其是在服务设施配置试验中,这是QEA-SOFA算法中量子特性对搜索解质量的主要贡献。
5 结论本文提出面向设施配置空间优化量子进化算法,用于求解高维多峰空间优化问题,改善传统算法易陷入局部搜索的不足,搜索解质量得到提升,并将其应用于城市急救设施配置空间优化。本文算法可更好地适应城市耦合环境下地理现象相关性和异质性约束,编码表达状态更多,对空间异质区域局部搜索具有更大探测尺度,这表明量子进化机制在求解地理空间优化问题中具有巨大潜力。但是,当前研究仍存在不足:①城市专项服务设施规划导向、时空地理信息是城市公共基础设施管控、规划的研究基础[39],本文侧重于算法模型,而弱化了城市公共基础设施规划理论、时空信息获取与分析方法,未来研究中将加强论述;②QEA-SOFA算法未能完全从理论层面开展收敛性数理证明;③当前量子进化算法实现了与设施配置的融合应用,但量子并行高性能优势尚未发挥,仍处于地理优化问题量子方法研究的萌芽阶段。QEA-SOFA算法仍运行于经典计算机(冯诺依曼架构计算框架)上,无法完全克服模拟量子编码和量子变异算子的耗时缺陷,未来研究工作将重点围绕如何将地理优化量子算法运行于量子计算机[40],如:D-Wave(量子退火)、IonQ(离子阱)、Rigetti(超导),实现在性能和质量的双提升研究[17]。
| [1] |
LI Wenwen, CAO Kai, CHURCH R L. Cyberinfrastructure, GIS, and spatial optimization: opportunities and challenges[J]. International Journal of Geographical Information Science, 2016, 30(3): 427-431. DOI:10.1080/13658816.2015.1112906 |
| [2] |
赵翔. 土地利用优化配置的多目标人工免疫优化模型研究[D]. 武汉: 武汉大学, 2013. ZHAO Xiang. Land use allocation optimization models based on multi-objective artificial immune systems[D]. Wuhan: Wuhan University, 2013. |
| [3] |
黎夏, 李丹, 刘小平. 地理模拟优化系统(GeoSOS)及其在地理国情分析中的应用[J]. 测绘学报, 2017, 46(10): 1598-1608. LI Xia, LI Dan, LIU Xiaoping. Geographical simulation and optimization system (GeoSOS) and its application in the analysis of geographic national conditions[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1598-1608. DOI:10.11947/j.AGCS.2017.20170355 |
| [4] |
王楠, 吴巍, 胡细英, 等. 大型交通设施对房地产价格影响研究进展与评述[J]. 城市发展研究, 2018, 25(5): 13-18. WANG Nan, WU Wei, HU Xiying, et al. Research progress on the impacts of great traffic facilities on housing price[J]. Urban Development Studies, 2018, 25(5): 13-18. |
| [5] |
MCCORMACK R, COATES G. A simulation model to enable the optimization of ambulance fleet allocation and base station location for increased patient survival[J]. European Journal of Operational Research, 2015, 247(1): 294-309. DOI:10.1016/j.ejor.2015.05.040 |
| [6] |
TONG Daoqin, MURRAY A T. Spatial optimization in geography[J]. Annals of the Association of American Geographers, 2012, 102(6): 1290-1309. DOI:10.1080/00045608.2012.685044 |
| [7] |
SHAREEFH, ISLAMM M, MOHAMEDA. A review of the stage-of-the-art charging technologies, placement methodologies, and impacts of electric vehicles[J]. Renewable and Sustainable Energy Reviews, 2016, 64: 403-420. DOI:10.1016/j.rser.2016.06.033 |
| [8] |
崔建鑫, 赵海霞. 城镇污水处理设施空间优化配置研究[J]. 中国环境科学, 2016, 36(3): 943-952. CUI Jianxin, ZHAO Haixia. Method for spatial optimal allocation of urban sewage treatment facilities[J]. China Environmental Science, 2016, 36(3): 943-952. DOI:10.3969/j.issn.1000-6923.2016.03.043 |
| [9] |
戴特奇, 廖聪, 胡科, 等. 公平导向的学校分配空间优化: 以北京石景山区为例[J]. 地理学报, 2017, 72(8): 1476-1485. DAI Teqi, LIAO Cong, HU Ke, et al. Secondary school allocation optimization towards equal access: a case study on Shijingshan District, Beijing[J]. Acta Geographica Sinica, 2017, 72(8): 1476-1485. |
| [10] |
DASKIN M S. Network and discrete location: models, algorithms, and applications[M]. 2nd ed Hoboken. New Jersey: John Wiley & Sons, Inc., 2013.
|
| [11] |
DASKIN M S. What you should know about location modeling[J]. Naval Research Logistics, 2008, 55(4): 283-294. DOI:10.1002/nav.20284 |
| [12] |
谢顺平, 冯学智, 都金康. 基于网络Voronoi图启发式和群智能的最大覆盖空间优化[J]. 测绘学报, 2011, 40(6): 778-784. XIE Shunping, FENG Xuezhi, DU Jinkang. Maximal covering spatial optimization based on network Voronoi diagrams heuristic and swarm intelligence[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 778-784. |
| [13] |
程敏, 崔晓. 基于多目标改进免疫算法和GIS的养老机构空间配置优化研究: 以上海市虹口区为例[J]. 地理科学, 2018, 38(12): 2049-2057. CHENG Min, CUI Xiao. Spatial optimization configuration of the residential care homes based on the multi-objective improved immune algorithm and GIS: a case study of Hongkou District in Shanghai[J]. Scientia Geographica Sinica, 2018, 38(12): 2049-2057. |
| [14] |
王海鹰, 秦奋, 张新长, 等. 基于蚁群优化算法的城市生态用地空间规划模型[J]. 地理科学, 2017, 37(3): 426-436. WANG Haiying, QIN Fen, ZHANG Xinchang, et al. The spatial planning model of urban ecological land based on ant colony optimization algorithm[J]. Scientia Geographica Sinica, 2017, 37(3): 426-436. |
| [15] |
FARAHANI R Z, FALLAH S, RUIZ R, et al. OR models in urban service facility location: a critical review of applications and future developments[J]. European Journal of Operational Research, 2019, 276(1): 1-27. |
| [16] |
朱阿兴, 闾国年, 周成虎, 等. 地理相似性: 地理学的第三定律?[J]. 地球信息科学学报, 2020, 22(4): 673-679. ZHU Axing, LV Guonian, ZHOU Chenghu, et al. Geographic similarity: third law of geography?[J]. Journal of Geo-Information Science, 2020, 22(4): 673-679. |
| [17] |
王宝楠, 水恒华, 王苏敏, 等. 量子退火理论及其应用综述[J]. 中国科学: 物理学力学天文学, 2021, 51(8): 5-17. WANG Baonan, SHUI Henghua, WANG Sumin, et al. Theories and applications of quantum annealing: a literature survey[J]. Scientia Sinica(Physica, Mechanica & Astronomica), 2021, 51(8): 5-17. |
| [18] |
范桁. 量子计算与量子模拟[J]. 物理学报, 2018, 67(12): 16-25. FAN Heng. Quantum computation and quantum simulation[J]. Acta Physica Sinica, 2018, 67(12): 16-25. |
| [19] |
焦李成, 李阳阳, 刘芳, 等. 量子计算、优化与学习[M]. 北京: 科学出版社, 2017. JIAO Licheng, LI Yangyang, LIU Fang, et al. Quantum computation, optimization and learning[M]. Beijing: Science Press, 2017. |
| [20] |
HAN K H, KIM J H. Genetic quantum algorithm and its application to combinatorial optimization problem[C]//Proceedings of the 2000 Congress on Evolutionary Computation. La Jolla, CA, USA: IEEE, 2002: 1354-1360.
|
| [21] |
钱洁, 王保华, 郑建国, 等. 多重二次背包问题的量子进化求解算法[J]. 计算机学报, 2015, 38(8): 1518-1529. QIAN Jie, WANG Baohua, ZHENG Jianguo, et al. A quantum evolutionary algorithm for quadratic multiple knapsack problem[J]. Chinese Journal of Computers, 2015, 38(8): 1518-1529. |
| [22] |
吴伟彬, 刘哲, 杨昊, 等. 后量子密码算法的侧信道攻击与防御综述[J]. 软件学报, 2021, 32(4): 1165-1185. WU Weibin, LIU Zhe, YANG Hao, et al. Survey of side-channel attacks and countermeasures on post-quantum cryptography[J]. Journal of Software, 2021, 32(4): 1165-1185. |
| [23] |
宋慧超, 刘晓楠, 王洪, 等. 基于Grover搜索算法的整数分解[J]. 计算机科学, 2021, 48(4): 20-25. SONG Huichao, LIU Xiaonan, WANG Hong, et al. Integer decomposition based on Grover search algorithm full text replacement[J]. Computer Science, 2021, 48(4): 20-25. |
| [24] |
SMITH-MILES K, LOPES L. Measuring instance difficulty for combinatorial optimization problems[J]. Computers & Operations Research, 2012, 39(5): 875-889. |
| [25] |
周亮. 实数编码量子进化算法及在投资组合中的应用[D]. 上海: 东华大学, 2012. ZHOU Liang. Real-coded quantum evolutionary algorithm and its application in portfolio selection[D]. Shanghai: Donghua University, 2012. |
| [26] |
HAN K H, KIM J H. Quantum-inspired evolutionary algorithm for a class of combinatorial optimization[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(6): 580-593. |
| [27] |
杨淑媛, 焦李成, 刘芳. 量子进化算法[J]. 工程数学学报, 2006, 23(2): 235-246. YANG Shuyuan, JIAO Licheng, LIU Fang. The quantum evolutionary algorithm[J]. Chinese Journal of Engineering Mathematics, 2006, 23(2): 235-246. |
| [28] |
赵新泉, 彭勇行. 管理决策分析[M]. 2版. 北京: 科学出版社, 2000. ZHAO Xinquan, PENG (Yong)(Hang|Xing). Management decision analysis[M]. 2nd ed. Beijing: Science Press, 2000. |
| [29] |
高辉, 张锐. 改进实数编码量子进化算法及其在参数估计中的应用[J]. 控制与决策, 2011, 26(3): 418-422. GAO Hui, ZHANG Rui. Improved real-coded quantum evolutionary algorithms and its application on parameter estimation[J]. Control and Decision, 2011, 26(3): 418-422. |
| [30] |
李昆仑, 关立伟. 实数编码量子共生演算法及其在云任务调度中的应用[J]. 计算机应用研究, 2019, 36(3): 786-791. LI Kunlun, GUAN Liwei. Real-coded quantum SOS algorithm and its application in cloud task scheduling[J]. Application Research of Computers, 2019, 36(3): 786-791. |
| [31] |
覃朝勇, 郑建国, 朱佳俊. 一种实数编码量子进化算法及其收敛性[J]. 控制与决策, 2009, 24(6): 854-858, 863. QIN Chaoyong, ZHENG Jianguo, ZHU Jiajun. Real-coded quantum-inspired evolutionary algorithm and its convergence[J]. Control and Decision, 2009, 24(6): 854-858, 863. |
| [32] |
张宇献, 钱小毅, 彭辉灯, 等. 基于等位基因的实数编码量子进化算法[J]. 仪器仪表学报, 2015, 36(9): 2129-2137. ZHANG Yuxian, QIAN Xiaoyi, PENG Huideng, et al. Real-coded quantum evolutionary algorithm based on allele[J]. Chinese Journal of Scientific Instrument, 2015, 36(9): 2129-2137. |
| [33] |
钱小毅. 基于等位基因量子进化算法的经纱断头率优化研究[D]. 沈阳: 沈阳工业大学, 2016. QIAN Xiaoyi. Study on the end breakage rate optimization for warp based on allele quantum evolutionary algorithm[D]. Shenyang: Shenyang University of Technology, 2016. |
| [34] |
高辉, 徐光辉, 张锐, 等. 实数编码量子进化算法[J]. 控制与决策, 2008, 23(1): 87-90. GAO Hui, XU Guanghui, ZHANG Rui, et al. Real-coded quantum evolutionary algorithm[J]. Control and Decision, 2008, 23(1): 87-90. |
| [35] |
BROTCORNE L, LAPORTE G, SEMET F. Ambulance location and relocation models[J]. European Journal of Operational Research, 2003, 147(3): 451-463. |
| [36] |
WANG Fahui. Measurement, optimization, and impact of healthcare accessibility: amethodological review[J]. Annals of the Association of American Geographers, 2012, 102(5): 1104-1112. |
| [37] |
张宇山. 进化算法的收敛性与时间复杂度分析的若干研究[D]. 广州: 华南理工大学, 2013. ZHANG Yushan. Some studies on the convergence and time complexity analysis of evolutionary algorithms[D]. Guangzhou: South China University of Technology, 2013. |
| [38] |
何键浩, 李绿周. 量子优化算法综述[J]. 计算机研究与发展, 2021, 58(9): 1823-1834. HE Jianhao, LI Lüzhou. An overview of quantum optimization[J]. Journal of Computer Research and Development, 2021, 58(9): 1823-1834. |
| [39] |
JIA Jingyuan, WANG Bo. The development of intelligent operation method of urban public infrastructure driven by accurate spatio-temporal information[J]. Journal of Geodesy and Geoinformation Science, 2021, 4(2): 27-35. |
| [40] |
GUO Mengyu, WANG Shaowen. Quantum computing for solving spatial optimization problems[M]. Cham: Springer International Publishing, 2020: 97-113.
|



