2. 中国地质大学(武汉)国家地理信息系统工程技术研究中心, 湖北 武汉 430074
2. National Engineering Research for Geographic Information System, China University of Geosciences, Wuhan 430074, China
兴趣点(POI)数据是电子地图、导航平台、专题地图等的重要组成部分,反映餐饮、文娱、住宿等多种城市活动场所信息。受益于基于位置服务(LBS)的普及,POI数据表现出数据量大、获取迅速、来源多样、商业价值高等特点,其数据产品在城市规划、社会服务、应急管理及智慧城市等领域具有广泛应用[1-6]。
作为POI数据的重要来源,众源地理信息数据受非专业收集模式影响,相关专题数据质量参差不齐,影响POI数据产品的可靠性与准确性。例如,OSM平台的POI数据,其类别或标签特征往往存在标注错误或信息丢失的问题,如何利用空间智能模型自动纠正错误标签或补全缺失信息,是该领域的一个重要研究方向。
不同于信息科学领域的一般标签预测任务,POI特征依赖于空间关系的定义和语义信息挖掘。例如,文献[7]提出利用POI名称文本数据,结合分词技术和向量空间模型构建POI目标特征,以此输入朴素贝叶斯模型预测样本类别的条件概率。虽然POI名称对于部分类别预测具有一定适应性,但POI标签类别与其命名并无本质联系,建立的相关模型对不同场景的泛化能力也较弱。文献[8—9]利用用户访问POI的时间、用户人口统计信息及附近商家信息构建Placer分类器,由决策树模型输出POI标签预测概率。文献[10—11]提出了一个潜在的概率生成模型,融合了用户签到行为的多源数据,包括空间位置信息、时间信息以及用户自身的配置文件等。同样是基于用户的签到行为特征。文献[12]综合利用了更多的签到统计数据,首先提取POI的显式特征,然后基于用户签到行为间的相关关系构建相似POI网络,以此提取POI间的隐式特征,支持显式特征和隐式特征耦合下的POI标签预测。然而,传统方法大多需要利用位置、语义、文本、行为等多源数据;考虑到不同场景下数据获取的有限性,本文尝试利用POI最基本的位置和类别信息推测目标缺失的标签,提高方法在实际环境下的适应性。
针对标签预测问题,常规前馈神经网络[13]须假设各类别的对象数量具有均衡性,而对于数量相对较少的类别,传统模型容易将其错分至数量较多的类别,难以顾及不平衡类别间的预测精度。事实上,POI数据具有典型的不平衡类别分布,不同POI类型承担不同的城市功能服务,部分类别在城市系统中占主要地位,如餐厅等。如何有效顾及POI数据的类别不均衡性与空间依赖等特征,是设计有效神经网络标签预测模型的关键。为了解决不平衡数据集分类问题,许多专家学者从数据和算法两个层面开展了相关研究。在数据层面上,欠采样或过采样的方法占据主流。文献[14]提出Tmoek-links欠采样方法,寻找互为最邻近的两类样本来去除多数类样本中的噪音;文献[15]提出的SMOTE方法以线性插值的方式在样本间生成少数类样本从而对数据过采样。在算法层面,代价敏感学习和集成学习影响力较为广泛。文献[16]将较高的分类代价分给少数类,通过各类间不同的错分代价分配提高分类器对少数类的关注度。文献[17—19]分别提出了集成学习中著名的Bagging算法[17]、Boosting算法[18]及其变体随机森林[19]。它们都是基于一系列的子分类器,通过某种规则将各个子分类器的结果整合起来作为最终分类结果。但对POI数据集而言,现有的不平衡数据集处理方法在分类精度的提高上始终有限。
本文提出一种基于多层次类别组织的神经网络模型,不同于神经网络内部多层次的概念,该多层次神经网络模型是在POI多层次类别构建的基础上,以单个前馈神经网络作为模型的分类结点,在每一个神经网络分类结点进行两个POI类别集合的分流,从而形成一个“金字塔”式的多层次网络模型。相较于传统模型直接在单一层面上将对象划分至某一类别,本文模型考虑了不同类别的不平衡性,将少数类合并为一个大类,以此平衡与其他现有大类的数量差异,解决神经网络对少数类的泛化能力不足的问题,提高POI标签预测精度与众源地理信息数据质量的水平。
1 POI特征矢量初始化参考地理学第一定理,POI目标与其周围不同地理范围内各类别POI的数量分布具有潜在的相关关系。因此,推断某一POI标签可由其邻近空间的POI分布特征分析实现。但如何定义邻近空间以及提取多类型POI分布信息是该步骤的关键。传统方法往往基于单距离邻域,而对于不同的地理上下文环境,单一硬性边界容易丢失空间依赖关系的多尺度信息,生成不完备的特征矢量空间,进而影响POI分类器的标签预测精度。因此,本文提出一种基于多距离邻域的POI特征矢量化方法。
具体上:对于有M个类别共N条POI记录的POI数据集,假设Xn对应第n条POI记录,Xmi对应第m个类的第i条POI记录(i在第m个类内遍历),两者空间距离为dnmi。构建目标Xn的K级多邻域缓冲区集合D,存储k个顺序排列的缓冲区距离边界二元组,并统计落入各级别缓冲区范围的不同类别POI点的数量,以此生成Xn的特征矢量。假设第m个POI类的数据量为mJ,则该类落入Xn的第Dk个缓冲区的目标计数函数Count表示为
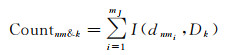 (1)
(1)
式中,计数判定函数I的定义为
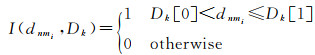 (2)
(2)
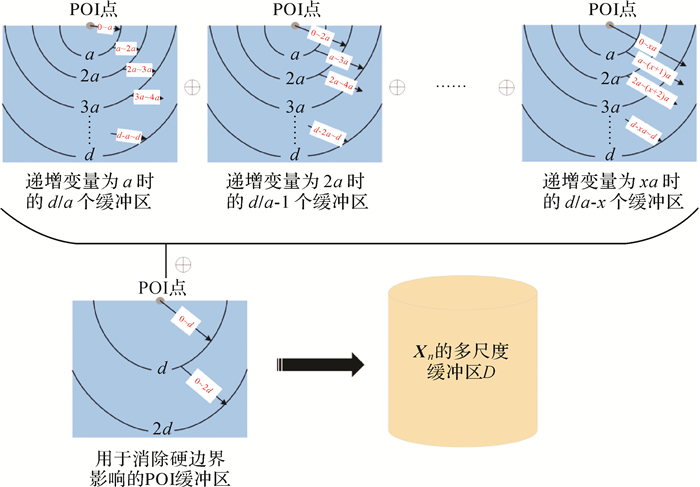
基于以上定义,首先将Countnm&k(k=1, 2, …, K)作为目标Xn特征空间的第((m-1)·K+k)个维度,然后依次构建Xn在M个类上的完备特征空间,最后生成所有POI点的特征矢量。具体的邻近空间构建策略如图 1所示。对于POI目标的邻近范围d,首先按照缓冲区的递增变量a,构建目标POI的[d/a]个圆形(或环形)缓冲区,其缓冲距离区间的集合为{(0, a), (a, 2a), (2a, 3a), …, ([d/a]×a, d)};然后,为顾及不同距离邻域内以及跨越缓冲区边界的空间关系,以2a为缓冲区递增变量,继续生成POI的[d/a]-1个圆形(或环形)缓冲区,其缓冲距离区间的集合为{(0, 2a), (a, 3a), (2a, 4a), …, ([d/a]×a-a, d)};迭代以上步骤,可分析多种距离邻域、跨越不同范围的空间关系;最后,引入距离区间{(0, d)}的圆形缓冲区和{(d, 2d)}的环形缓冲区,分别用以消除邻近范围d的内硬边界与外硬边界的影响。
|
| 图 1 兴趣点的多尺度缓冲区构建(Xn为当前POI点) Fig. 1 The construction of multi-scale buffering of POIs (Xn is the object of interest) |
由以上建模方式可见,邻域范围d是提取POI空间依赖特征的重要考虑因素。在城市分析领域,有研究者指出400~600 m的空间距离足以模拟城市街区和街道等尺度上的空间交互作用[20-21]。但POI通常与多个街区的空间背景有相互作用,因此选择1000 m作为POI对象间的基本交互范围。文献[22]也证实了1000 m对于POI位置评价的有效性。图 2以包含10个类别的POI数据集为例,设置邻近范围d为1000 m,缓冲区递增变量a为20 m,构建6个递增尺度(即20、40、60、80、100、1000 m)的缓冲区集合,则该中心POI点将生成2420维(即(50+49+48+ 47+46+2)×10维)特征属性。此外,为训练本文模型,采用One-Hot技术[23](即采用N位状态寄存器对N种类别进行独立编码,且任意时刻只有一个有效状态位)编码POI数据的类别信息。由此生成的特征矢量不仅包含有多距离邻域空间的POI分布信息,而且可表示POI的语义类别特征。

|
| 注:针对邻近空间中的某一类POI,将生成242维特征;因此,如果数据包含10类POI,将总共生成2420维的特征向量。 图 2 兴趣点的特征空间描述示例 Fig. 2 Illustration of the feature space of POIs |
2 多层次神经网络模型
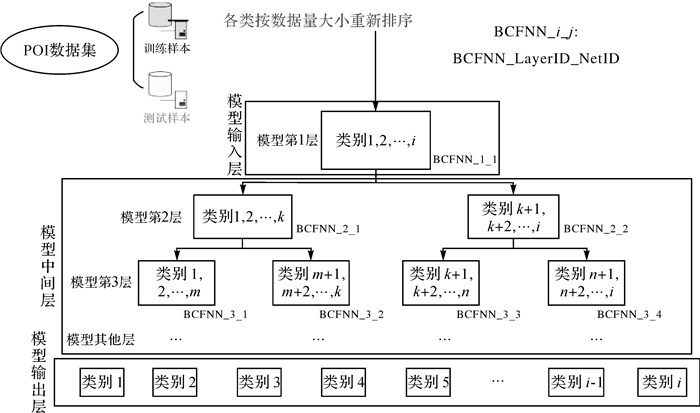
不同类型POI的数据量具有较高的异质特征,部分POI类型的数量差异可达数百倍(如餐厅与影剧院),这种不平衡分布是限制神经网络分类效果的关键因素。针对以上问题,部分学者采用集成学习、数据欠采样及数据过采样等策略[14-19],但对于提高POI标签预测精度的作用有限。相关研究指出[16],神经网络在处理分类问题上要优于传统算法,尤其是在二分类问题上的表现比多分类问题更为精确。本文立足于神经网络的二分类能力,耦合多个二分类前馈神经网络(binary classification feedforward neural network,BCFNN)搭建多层次POI标签预测模型,将POI多分类问题分解为层次二分类任务,以此提高模型泛化能力。具体多层次网络模型如图 3所示。
|
| 图 3 针对兴趣点标签预测的多层次模型框架 Fig. 3 The hierarchical model framework for predicting labels of POIs |
本文方法旨在通过对POI类型的层次组织,由多个原始类合并成类系,以此平衡原始POI类型数量的差异。具体采用“粗分-细分”的策略在不同层次对POI类型进行预测,提高单层次模型的预测精度。理论上,当各个类别的数据量均衡(或在同一数量级)时,模型具有[log2(i)]层,其中第j(j=1、2、…、[log2(i)])层有2j-1个分类器;每个分类器负责类系(每个类系是由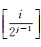

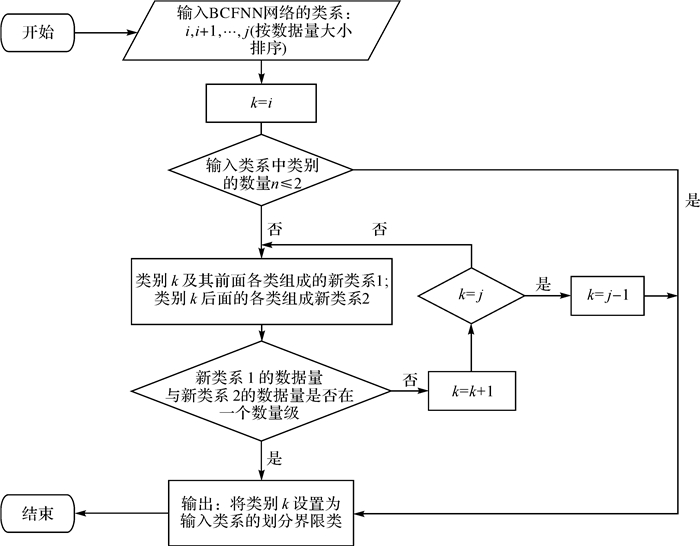
|
| 图 4 兴趣点类系划分流程 Fig. 4 The workflow of merging the classes of POIs |
具体过程为:
(1) 将输入类系中的各个类按数据量大小重新排序,得到类别集合{i、i+1、…、j}。设类别k为类系二分的界限类,类别k及其前面各类组成新类系1,类别k后面各类组成新类系2。
(2) 按顺序将类别ID赋值给变量k,判断以类别k为界限类而形成的新类系1与新类系2的数据量是否在同一数量级。若是,则将类别k作为输入类系的二分界限类进行输出,若不是,则取下一个类赋值给k并重复步骤(2)的判断。
(3) 需要注意的是,如果k被赋值到最后一个类别j,则直接选取倒数第2个类别j-1作为界限类,以此降低数据不平衡的影响;另外,输入的类系中只有两个类别时,则直接以排序后的第一个类作为界限类。
因此,本文提出的多层次模型是按数据集中各个类别数量的大小关系逐级分层构建的,模型每一层的BCFNN网络为下一层的BCFNN网络提供类系再次细分的数据与对应的标签,直至每一个BCFNN网络划分的类系只包含一个类别,则完成POI分类的工作。模型构建的思想借鉴于传统机器学习的决策树模型,区别在于该模型中每一层的每一个结点是基于BCFNN网络而非具体的类别判定条件,避免人工制定规则的限制。
该模型的BCFNN网络使用sigmoid函数为激活函数,L1范数函数为损失函数,并采用Adam优化算法对损失函数Loss求最小化极值,通过反向传播实现对BCFNN相关参数的优化。
3 试验与评价 3.1 试验数据试验数据来源于广州市中心城区的POI数据,包括10种常用的POI类型,依据高德地图的标签分类体系,其具体信息如图 5和表 1所示。从中可知,广州市的POI类型分布具有较显著的不平衡特征,餐厅、超市、生活服务3类POI数量占比超过65%,对模型预测效果构成较大挑战。

|
| 图 5 广州市城市设施兴趣点数据分布 Fig. 5 The distribution of Guangzhou POIs |
| 类别ID | 类别 | 描述 | 数据量 | 占比/(%) |
| 0 | 餐厅 | 餐饮服务大类的中餐厅、快餐厅、外国餐厅 | 21 682 | 35.7 |
| 1 | 超市 | 购物服务大类的便利店、超级市场 | 10 427 | 17.1 |
| 2 | 生活服务 | 生活服务大类中的美容美发店、物流速递、洗衣店 | 8796 | 14.5 |
| 3 | 娱乐场所 | 休闲体育服务大类的娱乐场所 | 2642 | 4.3 |
| 4 | 运动场馆 | 体育休闲服务大类的运动场馆 | 1019 | 1.6 |
| 5 | 影剧院 | 休闲体育服务大类的影剧院 | 161 | 0.2 |
| 6 | 医院 | 医疗保健服务大类的综合医院、专科医院、诊所 | 2164 | 3.5 |
| 7 | 药店 | 医疗保健服务大类的医药保健销售店 | 4648 | 7.6 |
| 8 | 宾馆酒店 | 住宿服务大类的宾馆酒店、旅馆招待所 | 3218 | 5.3 |
| 9 | 银行 | 金融保险服务大类的银行、自动提款机 | 5903 | 9.7 |
3.2 试验模型搭建
(1) 数据预处理。首先对广州POI数据进行特征矢量初始化,生成可直接用于多层次模型的输入向量;然后,对每个类按1∶6的测训比(测试样本量与训练样本量的比例)随机抽取数据,完成测试样本与训练样本的划分,具体如表 2所示。
| 类别ID | 测试样本数据量 | 训练样本数据量 |
| 0 | 3098 | 18 584 |
| 1 | 1490 | 8937 |
| 2 | 1257 | 7539 |
| 3 | 378 | 2264 |
| 4 | 146 | 873 |
| 5 | 23 | 138 |
| 6 | 310 | 1854 |
| 7 | 664 | 3984 |
| 8 | 460 | 2758 |
| 9 | 844 | 5059 |
| 总 | 8670 | 51 990 |
(2) 模型搭建。采用python语言与Pytorch深度学习框架构建多层次二分类神经网络模型。如图 6所示,首先将10个类别按照数据量递增排序,其ID排序结果为{5,4,6,3,8,7,9,2,1,0};然后按照第2节的POI类系划分方法,将各类型分层聚合,使得在同一个BCFNN网络下(即同一层)的两个类系具有相同级别的数据量,避免分布不均衡对模型精度的影响。
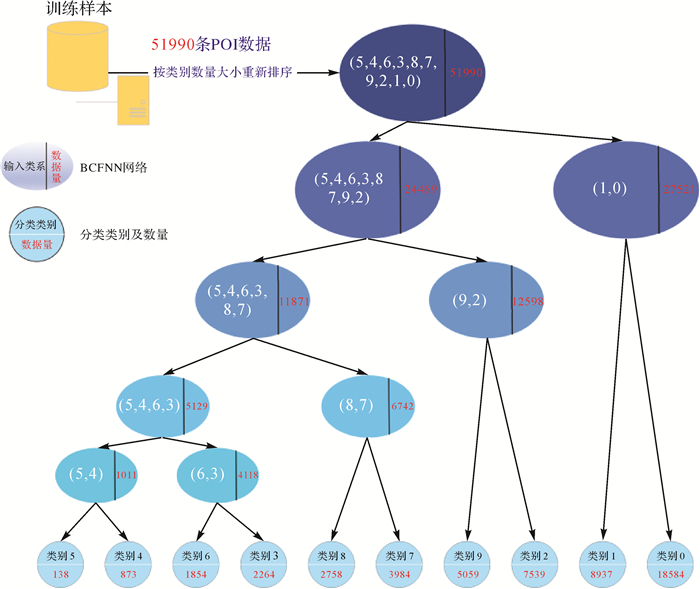
|
| 图 6 广州市兴趣点类型的多层次组织 Fig. 6 The hierarchical organization of Guangzhou POIs categories |
(3) 模型训练。依照上述搭建的基本模型结构,对各层的BCFNN网络采用多线程同步训练,记录下训练过程中的损失函数值并绘制损失曲线。如图 7所示,随着训练次数的增加各个BCFNN子模型的损失已趋于收敛。

|
| 图 7 各层次BCFNN子模型损失曲线 Fig. 7 The loss curves of BCFNN sub-models at each level |
3.3 模型预测
从总体数据中抽取1/7的测试样本作为标签预测目标,利用上述训练好的模型对每一个样本进行测试,将预测标签与真实标签进行对比,模型各个层次的预测目标数量见表 3。
| 模型层次 | 第1层 | 第2层 | 第3层 | 第4层 | 第5层 |
| 类系(组成的类别ID集合):每个类系预测获得的POI数量 | (4, 5, 3, 6, 7, 8, 2, 9):3537 (0, 1):5133 |
(4, 5, 3, 6, 7, 8):1434 (2, 9):2103 |
(4, 5, 3, 6):604 (7, 8):830 |
(4, 5):180 (3, 6):424 |
(4):153 (5):27 (3):219 (6):205 (7):599 (8):231 (2):1198 (9):905 (0):3924 (1):1209 |
为了验证POI多尺度特征对本任务的影响,本文在多层次预测模型的基础上分别设置了6个POI单一尺度特征驱动的预测对比试验,如图 8所示。结果表明,基于POI单一尺度特征的多层次模型的标签推断能力不如多尺度融合特征生成的模型,由此可见,本文提出的POI多尺度依赖特征的构建方法对提升多层次模型的预测能力具有显著的促进作用。
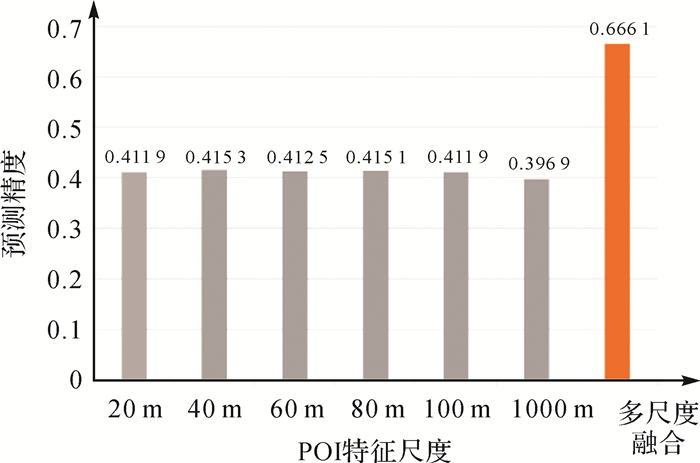
|
| 图 8 POI单一尺度和多尺度推断精度对比 Fig. 8 Accuracy comparison between single-scale prediction and multi-scale prediction |
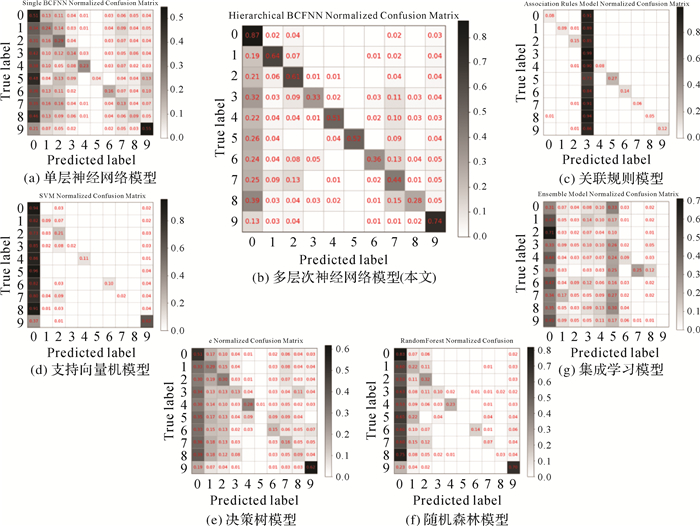
为了验证多层次神经网络模型对本任务的优势,本文选择当下流行的数据挖掘算法模型(即基于单层次神经网络模型[13]、基于关联规则模型[22]、基于集成学习模型[24])和传统的机器学习模型(基于随机森林模型[19]、基于决策树模型[25]、基于支持向量机模型[26])作为对比试验,在同等条件下(输入均为多尺度POI特征)对7种方法的模型预测能力进行比较。如图 9所示,通过对比各个模型之间的混淆矩阵不难发现,多层次神经网络模型在混淆矩阵的对角线上取得了较高的灰度值,这说明本文提出的多层次POI预测模型在先聚合小样本数据集再逐层划分POI类别的策略下,能够很好地对各个类别进行精准预测。相比之下,传统的数据挖掘模型和传统的机器学习算法在POI标签预测任务中稍显逊色:在POI分布存在严重分布不均衡的现实环境中,传统模型算法会通过提高对大样本数据集的拟合能力来降低模型损失从而提高整体的预测精度,而本文提出的多层次预测模型能较好地解决小样本类别预测精度低的问题。
|
| 图 9 POI类别预测模型的混淆矩阵对比 Fig. 9 The confusion matrix of different models |
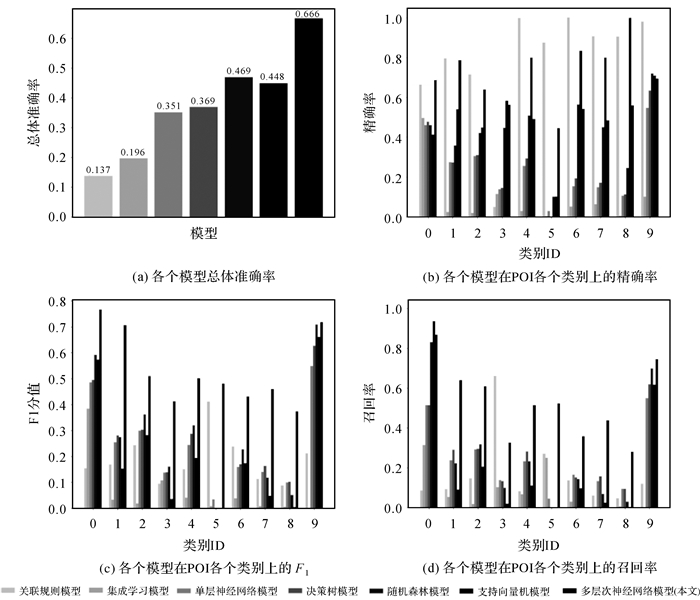
如图 10所示,为了进一步量化对比本文的多层次POI预测模型和其他6个模型的POI标签预测能力,采用准确率(Accuracy)、精确率(Precision)、召回率(Recall)、F1分值(F1 score)作为各个模型的评价指标,计算公式为
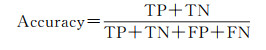 (3)
(3)
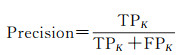 (4)
(4)
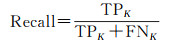 (5)
(5)
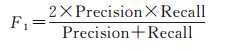 (6)
(6)
|
| 图 10 POI类别预测模型的评价指标对比 Fig. 10 The evaluation metrics of different models |
式中,TP表示模型认为POI为正类且其标签为正类标签;FN表示模型认为POI为负类且其标签为正类标签;FP表示模型认为POI为正类且其标签为负类标签;TN表示模型认为POI为负类且其标签为负类标签;下标K代表POI类别ID,K=0, 1, 2, …, 9。若规定对类别m而言,类别m为正类,除类别m外的其他类为负类。试验结果表明,多层次神经网络模型在仅基于POI位置信息与类别信息的前提下,POI类别的总体预测准确度达到66.6%,作为对比,传统的机器学习算法总体准确率不足50%,基于关联规则和集成学习算法的模型总体准确度甚至低于20%。这说明了本文多层次POI标签预测模型在POI标签预测任务上具有较高的可靠性。值得注意的是,在各个模型关于POI各类别的精确率对比上,总体准确率最低的关联规则模型在各POI类别上的精确率均高于本文模型。但结合两者的混淆矩阵不难发现,关联规则模型善于对特征较明显的POI进行分类,而对于在测试集中特征较模糊的POI,关联规则模型会趋向于将分类到某一个POI数量较多的类别上,以此来规避不必要的损失,但其带来的结果是总体准确率的大幅下滑。基于随机森林和基于支持向量机的模型具有相似的特点,它们在个别POI类别上有比本文模型有更高的精确率,但它们更倾向于将特征不够明显的POI统一划分到POI数量最多的类别上从而最小化模型损失,因此它们相较于关联规则模型有更高的准确率。相比于模型精确率的评价指标,F1分值是模型精确率和召回率的调和平均数,对模型的质量评价更具有可信度。本文模型在总体准确率占优的情况下,在POI测试集各个类别上的F1分值也远大于其他对比模型,这说明多层次预测方法较大程度改进了传统方法的效果以及对复杂现实场景的适应性。
4 结论POI是地理信息服务的重要数据源,其收集途径的多样性与便利性是POI数据产品的优势,但同时也带来了诸多的数据质量问题,例如标签缺失、错误等。如何增强众源POI数据特征是地理信息领域的热点问题。不同于一般的标签预测任务,POI类型分布具有显著的不平衡特征,综合考虑空间数据特有的依赖关系、多尺度等特征,发展高精度的神经网络预测模型具有重要价值。
本文旨在解决POI标签预测的两个关键问题,即多尺度特征矢量初始化、不平衡类型分布的标签预测。首先,依据空间依赖等地理学知识,提取目标周围POI类型分布信息,作为当前POI的特征空间;考虑到邻近空间的多尺度特性,提出了基于多缓冲区的特征矢量初始化方法,可有效考虑不同尺度空间关联对POI标签预测的影响。其次,针对不同POI类型的数据量差异,提出了一种新的多层次神经网络模型,将复杂的多分类问题分解为简单二分类任务,提高模型对不同类型数据的泛化能力和预测精度。由于本方法只需利用POI的位置数据和类别信息,其比较传统方法具有更广泛的应用场景。通过对比试验发现,多层次模型比传统关联规则模型与集成学习方法的精度更高。后续研究将基于多层次组织策略,融合POI多源属性数据(如签到行为数据等)[27-28],并基于不同地区POI分布特征设计空间邻域范围的自适应确定算法,进一步优化该模型,提高方法的预测精度。此外,多层次神经网络为空间目标的标签预测提供了一种新思路,不仅可用于POI数据,也可用于路网弧段、建筑物等其他类型目标。
| [1] |
FU Chun, TU Xiaoqiang, HUANG An. Identification and characterization of production-living-ecological space in a central urban area based on POI data: a case study for Wuhan, China[J]. Sustainability, 2021, 13(14): 7691. DOI:10.3390/su13147691 |
| [2] |
宋辞, 裴韬. 北京市多尺度中心特征识别与群聚模式发现[J]. 地球信息科学学报, 2019, 21(3): 384-397. SONG Ci, PEI Tao. Exploring polycentric characteristic and residential cluster patterns of urban city from big data[J]. Journal of Geo-Information Science, 2019, 21(3): 384-397. |
| [3] |
禹文豪, 艾廷华, 刘鹏程, 等. 设施POI分布热点分析的网络核密度估计方法[J]. 测绘学报, 2015, 44(12): 1378-1383, 1400. YU Wenhao, AI Tinghua, LIU Pengcheng, et al. Network kernel density estimation for the analysis of facility POI hotspots[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(12): 1378-1383, 1400. DOI:10.11947/j.AGCS.2015.20140538 |
| [4] |
蔡建南, 刘启亮, 徐枫, 等. 多层次空间同位模式自适应挖掘方法[J]. 测绘学报, 2016, 45(4): 475-485. CAI Jiannan, LIU Qiliang, XU Feng, et al. An adaptive method for mining hierarchical spatial co-location patterns[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(4): 475-485. DOI:10.11947/j.AGCS.2016.20150337 |
| [5] |
赵卫锋, 李清泉, 李必军. 利用城市POI数据提取分层地标[J]. 遥感学报, 2011, 15(5): 973-988. ZHAO Weifeng, LI Qingquan, LI Bijun. Extracting hierarchical landmarks from urban POI data[J]. Journal of Remote Sensing, 2011, 15(5): 973-988. |
| [6] |
HOU Gang, CHEN Lizhu. Regional commercial center identification based on POI big data in China[J]. Arabian Journal of Geosciences, 2021, 14(14): 1360. DOI:10.1007/s12517-021-07597-z |
| [7] |
杨小明. 电子地图兴趣点分类自动标注算法研究[J]. 网络安全技术与应用, 2015(3): 13-15. YANG Xiaoming. Research on automatic labeling algorithm of electronic map points of interest classification[J]. Network Security Technology & Application, 2015(3): 13-15. |
| [8] |
KRUMM J, ROUHANA D. Placer: semantic place labels from diary data[C]//Proceedings of 2013 ACM International Joint Conference on Pervasive and Ubiquitous Computing. Zurich, Switzerland: ACM Press, 2013: 163-172.
|
| [9] |
KRUMM J, ROUHANA D, CHANG Mingwei. Placer: semantic place labels beyond the visit[C]//Proceedings of 2015 IEEE International Conference on Pervasive Computing and Communications (PerCom). St. Louis, MO, USA: IEEE, 2015: 11-19.
|
| [10] |
HE Tieke, YIN Hongzhi, CHEN Zhenyu, et al. A spatial- temporal topic model for the semantic annotation of POIs in LBSNs[J]. ACM Transactions on Intelligent Systems and Technology, 2017, 8(1): 1-24. |
| [11] |
HEGDE V, PARREIRA J X, HAUSWIRTH M. Semantic tagging of places based on user interest profiles from online social networks[C]//Proceedings of the 35th European conference on Advances in Information Retrieval. New York, NY, USA: ACM Press, 2013: 218-229.
|
| [12] |
YE M, SHOU D, LEE W C, et al. On the semantic annotation of places in location-based social networks[C]//Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Hong Kong, China: ACM Press, 2011.
|
| [13] |
SHI Shaochong, CHEN Peng, ZENG Zhaolong, et al. STL- FNN: an intelligent prediction model of daily theft level[C]//Proceedings of the 9th International Conference on Computer Engineering and Networks. Singapore: Springer Singapore, 2020: 703-711.
|
| [14] |
TOMEK I. Two modifications of CNN[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1976. |
| [15] |
CHAWLA N V, BOWYER K W, HALL L O, et al. SMOTE: synthetic minority over-sampling technique[J]. Journal of Artificial Intelligence Research, 2002, 16: 321-357. |
| [16] |
THAI-NGHE N, GANTNER Z, SCHMIDT-THIEME L. Cost-sensitive learning methods for imbalanced data[C]//Proceedings of 2010 International Joint Conference on Neural Networks (IJCNN). Barcelona, Spain: IEEE, 2010: 1-8.
|
| [17] |
BREIMAN L. Bagging predictors[J]. Machine Learning, 1996, 24(2): 123-140. |
| [18] |
SCHAPIRE R E. The strength of weak learnability[C]//Proceedings of the Second Annual Workshop on Computational Learning Theory. Amsterdam Netherlands: Elsevier, 1989, 5(2): 197-227.
|
| [19] |
BREIMAN L. Random forests[J]. Machine Learning, 2001, 45(1): 5-32. |
| [20] |
PORTA S, STRANO E, IACOVIELLO V, et al. Street centrality and densities of retail and services in bologna, Italy[J]. Environment and Planning B: Planning and Design, 2009, 36(3): 450-465. |
| [21] |
OKABE A, SATOH T, SUGIHARA K. A kernel density estimation method for networks, its computational method and a GIS-based tool[J]. International Journal of Geographical Information Science, 2009, 23(1): 7-32. |
| [22] |
KASHIAN A, RAJABIFARD A, RICHTER K F, et al. Automatic analysis of positional plausibility for points of interest in OpenStreetMap using coexistence patterns[J]. International Journal of Geographical Information Science, 2019, 33(7): 1420-1443. |
| [23] |
梁杰, 陈嘉豪, 张雪芹, 等. 基于独热编码和卷积神经网络的异常检测[J]. 清华大学学报(自然科学版), 2019, 59(7): 523-529. LIANG Jie, CHEN Jiahao, ZHANG Xueqin, et al. One-hot encoding and convolutional neural network based anomaly detection[J]. Journal of Tsinghua University (Science and Technology), 2019, 59(7): 523-529. |
| [24] |
FRIEDMAN J, HASTIE T, TIBSHIRANI R. Additive logistic regression: a statistical view of boosting (With discussion and a rejoinder by the authors)[J]. The Annals of Statistics, 2000, 28(2): 1-6. |
| [25] |
MYLES A J, FEUDALE R N, LIU Yang, et al. An introduction to decision tree modeling[J]. Journal of Chemometrics, 2004, 18(6): 275-285. |
| [26] |
VISHWANATHAN S V M, NARASIMHA MURTY M. SSVM: a simple SVM algorithm[C]//Proceedings of the 2002 International Joint Conference on Neural Networks. Honolulu, HI, USA: IEEE, 2002: 2393-2398.
|
| [27] |
王圣音, 刘瑜, 陈泽东, 等. 大众点评数据下的城市场所范围感知方法[J]. 测绘学报, 2018, 47(8): 1105-1113. WANG Shengyin, LIU Yu, CHEN Zedong, et al. Representing multiple urban places' footprints from dianping.com data[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(8): 1105-1113. DOI:10.11947/j.AGCS.2018.20180110 |
| [28] |
朱婷婷, 涂伟, 乐阳, 等. 利用地理标签数据感知城市活力[J]. 测绘学报, 2020, 49(3): 365-374. ZHU Tingting, TU Wei, YUE Yang, et al. Sensing urban vibrancy using geo-tagged data[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(3): 365-374. DOI:10.11947/j.AGCS.2020.20190051 |




