2. 中国测绘学会, 北京 100830;
3. 西安科技大学测绘科学与技术学院, 陕西 西安 710054;
4. 武汉大学资源与环境科学学院, 湖北 武汉 430079
2. Chinese Society of Surveying and Mapping, Beijing 100830, China;
3. College of Geomatics, Xi'an University of Science and Technology, Xi'an 710054, China;
4. School of Resource and Environmental Science, Wuhan University, Wuhan 430079, China
人口始终是人类社会需要面对的基础性、全局性和战略性问题[1-3]。人口空间分布是指一定空间范围内人口群体的分布、集散及组合状况,反映了人与空间的关系,是重要的社会经济现象。文献[4]首次对昼夜人口进行了描述和区分,指出昼夜间人口变化是最基本、最主要、最频繁的城市人口时空变化模式。人塑造了城市,是城市的主体,同时,城市的复杂性也反映在市民群体行为的复杂性上。由于缺乏先进的技术手段,往往无法真实记录和量测城市人口的个体流动与整体趋势,人们对城市昼夜人口空间集聚的了解仍然十分有限。
人口空间化是以人口数量为对象,以数学模型和算法为手段,按照空间单元进行离散化人口处理,获取空间单元内人口数量的过程,用于反映人口在一定时间和一定空间中的分布状态。人口空间化方法是人口空间化研究的核心,文献[5—6]将这些方法分为两类:面插值方法和统计模型方法。面插值方法用于实现将人口数据从源区域(人口普查区域或大尺度区域)向目标区域的转换[7],包括面积比重法、表面生成法和回归分析法等[8]。面插值的前提是假设源区域内人口均匀分布,当目标区域较小时该方法误差较大,不适合在城市内部尺度上估算人口[9]。统计模型方法建立在人口数量与统计变量(影响因子)间的数学关系之上,常见的变量包括城市面积、土地利用类型面积、居住单元数量、夜光遥感像元和手机信令等。其中,“人口—城市面积”关系模型基于城市人口异速增长理论[10],该模型仅适用于50~250万人口的城市,在城市内部尺度上并不适用[11-12]。“人口—土地利用”关系模型和“人口—建筑单元”关系模型则是将城市平面化,忽视了城市人口的立体分布,并不适合高楼林立的城市,实际情况中,单位地面面积的多层建筑的人口承载量远超过单层建筑(或地表)的人口量。“人口—夜光遥感”关系模型不仅存在灯光溢出(Overglow)问题,而且城市中人口与照明并不存在严格的对应(例如路灯、广告灯的光照不一定说明该处有人,而熄灯睡觉等形成的黑暗区又无法说明该处无人)。“人口—手机位置”关系模型是近年来兴起的一种人口空间化模型,该模型将城市人口与手机信号对等化,一方面会遗漏非手机人口(幼儿及部分老年人),另一方面在大范围手机关闭的情况下(例如夜晚休息)数据失真较严重。当前,更多的学者尝试集成多源数据研究人口空间化, 包括将高分遥感影像与机载激光雷达数据整合用于城市人口估算[7],整合DSM与DEM数据的人口空间化方案[13],整合遥感影像、土地利用、街区等多源数据用于人口空间化[14],将交通和POI数据整合研究城市人口分布[15],将多智能体模型与建筑信息整合开展人口分布模拟研究[16],将土地利用和夜间灯光数据整合优化人口空间化模型[17-18]等。
以上研究都未涉及人口空间分布的时态。人口集聚是一种复杂的社会行为,是一个时间动态变量,其分布在每日和季节循环中都有不同。文献[19—21]利用土地利用数据模拟了北京市海淀区和南京市部分区域的人口昼夜变化。文献[22—23]基于建筑空间和互联网信息分别模拟了成都市青羊区和北京市主城区的人口昼夜变化。文献[24]基于移动电话位置数据研究了捷克布拉格市的人口昼夜变化。总体来看,昼夜人口分布的研究文献较少,多采用单因子估算,精度不高,对昼夜人口空间集聚的探讨也不足。基于此,本文基于城市人群的时间地理特征,从城市大数据中挖掘并模拟城市人群社会时空行为,在此基础上计算百米格网城市昼夜人口时空分布并分析集聚特征与模式,以期为城市演化机理研究提供依据。
1 研究区和数据来源 1.1 研究区概况武汉是我国中部地区的经济中心、长江经济带核心城市。2018年全市常住人口1 108.10万人[25],中心城区常住人口624.2万,是我国中部地区人口最多的城市。本文选取武汉市中心城区作为研究区,包括江岸区、江汉区、硚口区、汉阳区、武昌区、青山区(化工区)和洪山区。研究区总面积695.8km2,平均人口密度8971人/km2,是全市平均人口密度的6.94倍,是城市人口核心密集区。
1.2 数据来源本文采用的数据包括人口统计数据、heatmap数据、房屋建筑调查数据、地表覆盖数据及基础地理信息数据。空间数据坐标系统为2000国家大地坐标系统(CGCS2000),采用平面坐标(高斯-克吕格3°带投影,中央经线114°E),坐标单位m。采用规则格网作为人口空间基本单元,尺度为100 m×100 m。
人口统计数据是人口空间化的源数据。本文采用社区人口调查数据,来源于武汉市公安局与市统计局(2018年)。该数据以社区为采集单元,为工作日晚上或双休日入户采集的常住人口数据,数据按照性别、年龄段分类,是本文夜间人口计算的人口数据源。对于白天人口来说,没有一个单一、可测量的统计概念作为工具[26]。白天人口的位置取决于人的社会角色以及城市功能空间布局,角色和设施驱动人群产生通勤或其他形式的迁移。因此,白天人口的统计源区域应设定为范围更大的城区。但即使是城区,人口的跨区域流动仍然会造成区域内昼夜人口总数不等,有必要评估研究区白天人口的波动。通勤是人口跨区域流动的主要因素,包括4种状态:内部通勤(城区内→城区内,居住和就业均在中心城区)、内向通勤(城区外→城区内,居住在郊区,但在中心城区就业)、逆向通勤(城区内→城区外,居住在中心城区,但在郊区就业)及侧向通勤(城区外→城区外,居住和就业都在郊区)。文献[27]基于百度大数据和联通大数据对2018年武汉中心城区的4类通勤进行了计算,结果见表 1。
| 通勤方向 | 百度通勤量测量比例 | 联通通勤量测量比例 |
| 内部通勤 | 46.45 | 44.51 |
| 内向通勤 | 9.23 | 10.69 |
| 逆向通勤 | 8.73 | 10.70 |
| 侧向通勤 | 35.59 | 34.10 |
定义中心城区内向人口流动率γ=内向通勤比例-逆向通勤比例。由表 1可知,基于百度通勤量获得的γ=9.23%-8.73%=0.5%,该方法基于155万的百度用户记录。197万的联通用户记录则显示γ=10.69%-10.70%=-0.01%。本文又借鉴了《2018年中国城市通勤研究报告》[28],该报告采用城市大数据探测了实际职住比(为实际工作岗位与当地常住人口的比值)。报告显示2018年武汉中心城区的实际职住比为1.014 3,换算成γ=1.014 3-1=1.43%。3个结果较接近,为了降低数据波动,本文取3个结果的均值即γ=0.64%。数据表明,中心城区在工作日白天总人口呈微净流入。由此,将社区单元的白天人口数调整为(1+γ)×pi,pi为社区i的人口调查数据。
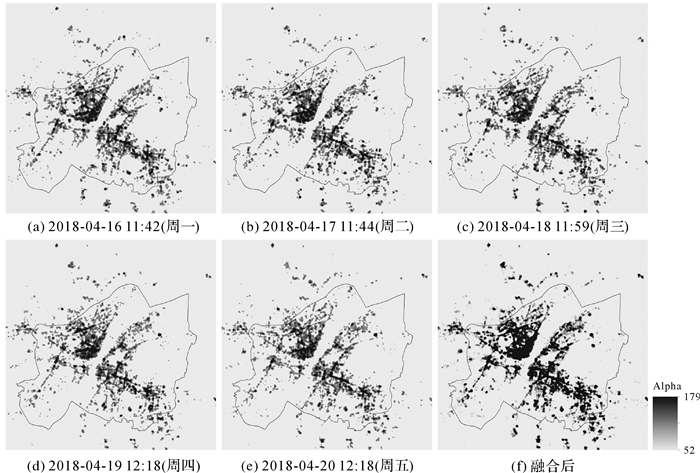
基于LBS平台的heatmap数据通过将手机信号聚类结果以有区别的色彩叠加在地图上,用于实时反映手机信号强度的空间集聚情况。如同夜光遥感感知人口分布的原理,heatmap并不直接对应人口数量,而是间接反映人口分布。虽然存在一人多机的情况,但考虑到这种情况的非普遍性以及非同时服务,忽略此情况。本文使用百度公司的heatmap数据(TIF格式),选择band_4通道(256级灰度Alpha),选取研究区2018年4月16日(周一)至4月20日(周五)连续5个工作日12点前后的heatmap数据。为降低单幅数据的人口涌动误差,采用多图像平均法融合,融合前后如图 1所示。
|
| 图 1 heatmap数据及多图像平均法融合后结果 Fig. 1 Heatmaps and fused heatmap from averaging of multiple image |
房屋建筑调查数据来自城市建筑专项调查数据(武汉,2017年),采集单元为楼体,包括建筑名称、层数、高度、建筑面积、基底面积、建筑分类等属性。建筑分类按照国家标准《城市用地分类与规划建设用地标准》(GB50137—2011)分为JA(公共管理与公共服务建筑)、JB(商业建筑)、JM(工业建筑)、JR(居住建筑)、JS(交通站场建筑)、JU(市政设施)、JW(仓储与物流建筑)及FF(其他建筑)共8类。本文中,幼儿园、中小学与高校在JA中通过建筑名称提取,居住建筑来源于JR。
地表覆盖数据来自地理国情监测,分为种植土地、林草覆盖、房屋建筑(区)、铁路与道路、构筑物、人工堆掘地、荒漠与裸露地和水域8个一级类,获取时间为2018年6月。
基础地理数据来自城市规划部门(2017年),包括中心城区边界、交通(一环、二环、三环及主干路)、行政区划等。
2 研究方法 2.1 场景构建白天人口的空间位置取决于人口角色及城市功能空间和设施的位置。这些空间及其设施吸引市民离开住所,推动通勤和其他形式的迁移。本质上,人口空间位置是他们活动的函数。个体行为可能带有主观成分,具有随机性,但群体行为具有一定的客观规律。行为地理学指出,空间中人的行为受到个体本身和社会的约束[29]:工作日白天,大部分人群处于工作、求学或通勤状态;夜间,人群主要以休憩和居家睡眠为主。参考已有研究成果[26-30],不失一般性,表 2归纳描述了城市群体在工作日期间的时间地理特征。
| 时间 | 行为 |
| 0:00—7:00 | 居家、睡眠 |
| 7:00—9:00 | 上班、上学及居家 |
| 9:00—12:00 | 以工作(室内、室外)和上学为主,并伴有生活类活动,如老年人购物、社交 |
| 12:00—14:00 | 以工作和上学所在场所休憩为主,午餐并伴有生活类活动 |
| 14:00—17:00 | 以工作(室内、室外)和上学为主,并伴有生活类活动,如老年人购物、社交 |
| 17:00—22:00 | 返家休憩、晚餐并伴有生活类活动,如购物、社交 |
| 22:00—0:00 | 居家、睡眠 |
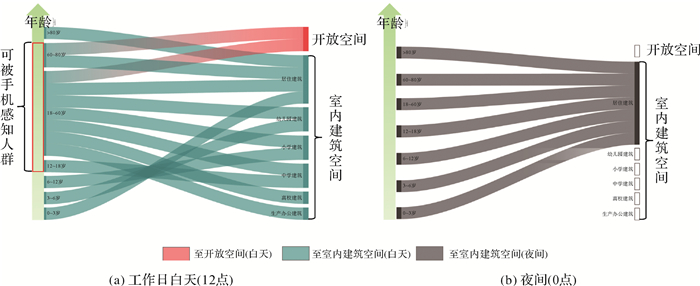
通过归纳表 2的群体行为,本文将城市空间划分为室外开放空间和室内建筑空间,将建筑细分为居住建筑、幼儿园建筑、中小学建筑、高校建筑和生产办公建筑。如何有效感知市民的空间位置是城市人口空间化的核心。《中国互联网络发展状况统计报告(43)》(中国互联网络信息中心) 显示,截至2018年12月,我国手机网民达8.17亿,我国绝大多数城区具备使用手机信号感知人口的条件。《2018年武汉市国民经济和社会发展统计公报》显示,2018年末全市手机用户达到1 684.4万,移动电话普及率为154.6部/百人。我国仅县级城市城区12岁以上青少年拥有智能手机的比例已达94.21%,在大城市中心城区这一比例则更高[31]。老年人拥有智能手机的比例一直未有参考文献,考虑到城市老年人口的生活现状,本文将研究区内能被手机感受的人口设置为12~80岁之间,即12(初中生)至80岁的区间人口可以被手机上网信号感知,相当于覆盖了城市中几乎所有独立活动人群。虽然6~12岁之间的小学生也存在携带手机的情况,文献[32]显示,由于学校管理的要求,主要是在上下学路上或家中使用,在校一般不使用。故本文将6~12岁之间的小学生归入非手机信号感知人群。对年龄段人口与时间及所处空间建立映射关系,绘制城市人群时空地理Sankey图(图 2)。图 2左侧表示年龄段,右侧表示城市空间。将人口设置为0~3岁、3~6岁、6~12岁、12~18岁、18~60岁、60~80岁和80岁以上共7个年龄段。空间划分为开放空间和室内建筑空间。图中连线表示年龄段人口(左节点)在标题时态下所处的空间(右节点),每一条连接线对应了人口结构变量与时空变量的一种组合,称为场景。
|
| 图 2 城市人群时空地理Sankey图 Fig. 2 Sankey map of spatio-temporal geography for urban population |
对于每一个场景,建立人口数量与统计变量的数学关系,变量主要基于建筑单元和手机信号。对所有场景分别人口空间化,场景覆盖区域所有人口,详见表 3,其中,白天人口记作dP,夜晚人口记作nP。结合表 3,目标区域i的白天人口数量dPi可以表示为
 (1)
(1)
| 序号 | 时间 | 场景 | 统计变量 | 人口空间化方法 | ||
| 记作 | 人口年龄 | 所处空间 | ||||
| 1 | 工作日白天12点 | dP1 | 0~3 | 居住建筑 | 建筑单元 | Ui=ωiP,Ui为目标区域i的人口数,P为源区域人口数, wi为估计参数。此处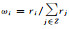 ,r表示居住建筑的建筑面积 ,r表示居住建筑的建筑面积 |
| 2 | dP2 | 3~6 | 幼儿园建筑 | 建筑单元 | Ui=ωiP,Ui、wi、P同前。此处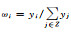 ,y表示幼儿园建筑的建筑面积 ,y表示幼儿园建筑的建筑面积 |
|
| 3 | dP3 | 6~12 | 小学建筑 | 建筑单元 | Ui=ωiP,Ui、wi、P同前。此处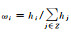 ,h表示小学建筑的建筑面积 ,h表示小学建筑的建筑面积 |
|
| 4 | dP4 | 12~18 | 中学建筑 | |||
| 5 | dP5 | 18~60 | 开放空间与室内建筑空间 | 手机位置 | Ui=ωiP,Ui、wi、P同前。此处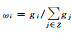 ,g表示手机信号的强度 ,g表示手机信号的强度 |
|
| 6 | dP6 | 60~80 | 开放空间和居住建筑 | |||
| 7 | dP7 | > 80 | 居住建筑 | 建筑单元 | Ui=ωiP,Ui、wi、P同前。此处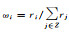 ,r表示居住建筑的建筑面积 ,r表示居住建筑的建筑面积 |
|
| 8 | 夜间0点 | nP1 | 0~3 | 居住建筑 | 建筑单元 |
Ui=ωiP,Ui、wi、P同前。此处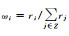 ,r表示居住建筑的建筑面积 ,r表示居住建筑的建筑面积 |
| 9 | nP2 | 3~6 | ||||
| 10 | nP3 | 6~12 | ||||
| 11 | nP4 | 12~18 | ||||
| 12 | nP5 | 18~60 | ||||
| 13 | nP6 | 60~80 | ||||
| 14 | nP7 | > 80 | ||||
式中,Pz(12 < age < 80)表示区域Z中年龄在12至80岁的人口,其他参数解释见表 3。
同样,目标区域i的夜间人口数量nPi可表示为
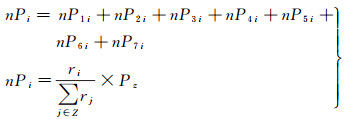 (2)
(2)
式中,Pz表示区域Z中所有年龄段的人口,其他参数说明同式(1)。
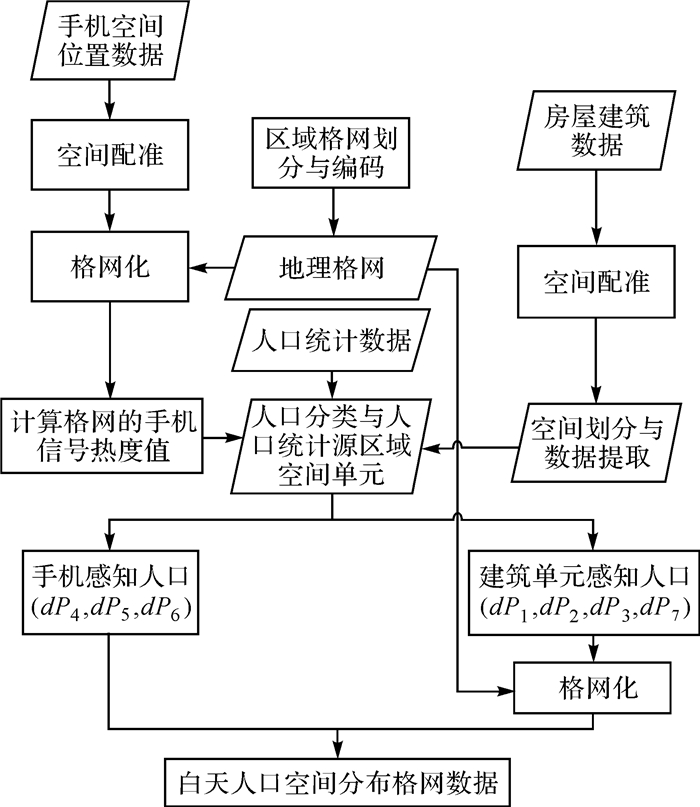
2.2 算法步骤 2.2.1 工作日白天人口空间化算法计算流程如图 3所示。
|
| 图 3 白天人口空间化计算流程 Fig. 3 Calculation flow chart of daytime population spatialization |
主要计算步骤如下。
(1) 确定空间坐标系(平面投影坐标系)。
(2) 按照确定的坐标系,生成空间统计单元(格网),格网大小决定了数据结果的空间分辨率。将计算涉及的其他空间数据统一到步骤(1)中的坐标系中。
(3) 手机位置数据处理。以heatmap数据感知携带手机人口,将heatmap数据进行地理配准,统一到步骤(1)中的坐标系。
(4) heatmap离散格网化,采用步骤(2)中的格网对heatmap进行分割,并按照式(3)计算每个格网gi的热度值hi
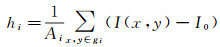 (3)
(3)
式中,Ai为格网gi中heatmap的像素规模,即像素数;I(x, y)为格网gi中(x, y)处的像素灰度值;I0为校准值,指无数据位置的灰度数值。
(5) 确定人口统计源区域单元。由于人口流动性,白天人口需要一个可量测的源区域作为人口基准单元。在该单元内按照图 2确定各年龄段内的人口数量。
(6) 根据表 3计算格网gi内手机信号感知的人群(dP4、dP5与dP6之和)。
(7) 重复步骤(6),直至完成区域内所有格网的手机信号感知人群。
(8) 根据表 3计算格网gi内建筑单元感知人群(dP1、dP2、dP3与dP7之和)。
(9) 重复步骤(8),直至完成所有格网的建筑单元感知的人群。
(10) 将步骤(7)和步骤(9)的结果进行空间叠加,计算结束。
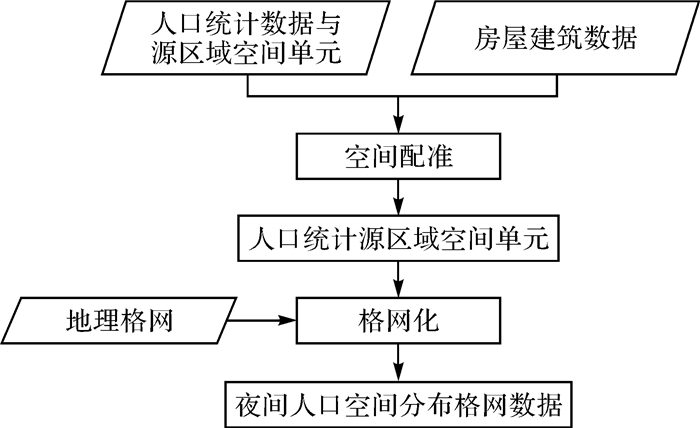
2.2.2 夜间人口空间化算法计算流程见图 4。
|
| 图 4 夜间人口空间化计算流程 Fig. 4 Calculation flow chart of nighttime population spatialization |
主要计算步骤如下。
(1) 设置坐标系,同白天人口的坐标系。
(2) 按照确定的坐标系,生成空间统计单元(同白天人口计算时的格网)并将其他空间数据统一到该坐标系中。
(3) 确定人口统计源区域单元。见表 3所示,夜间所有年龄段的人口空间化由建筑单元感知。
(4) 根据表 3计算格网gi中由建筑单元感知的人群。
(5) 重复步骤(4),直至完成区域内所有格网的人口计算,计算结束。
3 结果分析武汉市中心城区工作日白天(12点)与夜间(0点)的人口分布如图 5、图 6所示。本文依次从空间分布、空间梯度、昼夜差异与统计特征等方面展开分析。

|
| 图 5 中心城区人口密度分级图 Fig. 5 Classification map of population density in central urban area |
|
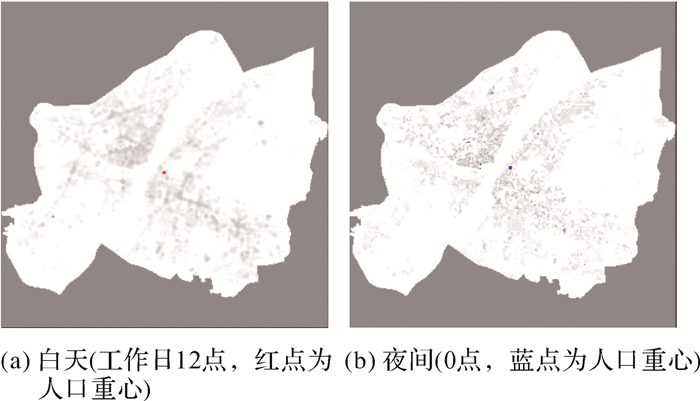
| 图 6 中心城区人口昼夜分布灰度图像 Fig. 6 Grayscale image of daytime and nighttime population distribution in central urban area |
3.1 昼夜人口空间分布特征
图 5显示昼夜人口分布具有空间耦合性。人口高密度区主要分布在两江沿岸,其中,长江北的人口密集区主要在两江交汇处的硚口区、江汉区及江岸区并沿长江北岸向东北延伸。长江南的人口密集区则主要分布在武昌区,从户部巷社区沿武珞路向东南延伸。由于图 5(a)、(b)采用了不同的分级阈值,其表现的昼夜人口聚集差异并不可比较。考虑到两幅地图基于相同格网,将格网图转化为栅格图像,栅格灰度按式(4)换算为0~255的灰度值
 (4)
(4)
式中,Gi为格网i的图像灰度;Pi为其人口数量;Pmax为两幅地图的人口最大值。人口最大值格网的灰度为0,无人口分布区域为白色(灰度值255),中心城区之外的无数据区域设置为背景色。转化后的人口分布灰度图像见图 6,此时22.139人/ 灰度单位。
计算结果显示,白天人口密度的最大值达到1580人/hm2,有人区域占中心城区的比例为45.02%,有人区域的平均人口密度为201人/hm2;夜晚人口密度的最大值达5534人/hm2,有人区域占中心城区的比例为41.98%,有人区域的平均人口密度为214人/hm2。无论昼夜,中心城区无人区域面积大于有人区域面积,这与区域内水域多(水域面积占比近20%)以及大面积城乡过渡区域有关。
人口重心可以简化为人口分布地图多边形的质心[33]。从力学的角度看,若把人口理解为区域平面上具有确定的点位和数值的散点集群,则该平面上集群力矩的平衡支撑点就是人口重心。重心可以有效说明要素在区域空间上的分布和集聚趋势。假设某地区包含n个子区,子区i的人口数量为Mi,几何中心坐标为(xi, yi),则该地区人口重心(X, Y)表示为
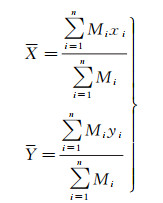 (5)
(5)
式(5)表明,影响人口重心的因素有两个:子区域空间位置与人口数量。在子区域空间位置不发生变化的情况下,影响因素则只是子区域的人口数量值。计算显示,研究区昼夜人口重心直线距离607.33 m,相距很近。两重心在东西向和南北向的间距分别为111.58 m和597.00 m,其中南北向间距相对于中心城区南北长度仅占2%。夜间人口重心位于白天人口重心北偏西10.59°方向。一般来说,人口分布主要受两个因素影响[34]:人口增长和迁移。1.2节表明中心城区人口呈微量净流入,人口增长的影响效果较弱。相距较近的昼夜人口重心说明中心城区的人口绝大多数在城区内部流动,且没有特别突出的主流向。南北方向的位移距离大于东西方向,夜间人口重心较白天人口重心偏北,说明白天工作时段流向中心城区南部的人口大于流向北部的人口。反映出当前中心城区并非纯粹的商业区,其间也夹杂着相当数量的居住区,人口流动以内部流动为主。
3.2 昼夜人口空间梯度特征图像学中频率表征图像的灰度变化程度,本节利用傅里叶变换分析人口集聚特征。令f(x, y)表示一幅大小为M×N图像中像元(x, y)的灰度,则f(x, y)的离散二维傅里叶变换为
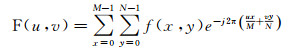 (6)
(6)
式中,u=0, 1, …, M-1;v=0, 1, …, N-1。
对图 6进行傅里叶变换,再经过频谱中心化(用(-1)x+y乘以输入图像)得到频谱中心化处理后的昼夜人口分布频谱图,如图 7所示。由于两幅图像具有同样幅面分布的同灰度背景,频谱能量的差异完全由昼夜人口空间分布差异导致。

|
| 图 7 中心城区人口昼夜分布图像频谱能量 Fig. 7 Image spectrum energy of daytime and nighttime population distribution in central urban area |
由图 7可知,能量由白天集中在低频部分(图 7(a))向夜间高频发散(图 7(b)),即白天人口分布频率能量集中在低频,夜间人口分布频率能量在高频和低频都有分布。这表明白天人口分布的范围更大,人口密度梯度相对较平滑,夜间人口分布的范围更小,人口密度梯度相对更尖锐,即中心城区夜间人口的聚集性大于白天人口,反映在图像上为夜间人口分布图像更清晰(图 6)。频谱图的中心部分出现两条亮度差异明显的特征线(图 8(b))。在图像频谱变换中频谱方向与原图像中地物分布垂直,频谱图显示出:长江(A线)与龟山蛇山方向为代表的城市山水交通轴(B线)是人口密度梯度变化最剧烈的两个方向,且A线的延伸长度大于B线。

|
| 图 8 中心城区人口昼夜分布图像频谱共轭表征 Fig. 8 Spectral conjugate map of daytime and nighttime population distribution in central urban area |
3.3 昼夜人口空间差异特征
以研究区白天有人区域的平均人口密度dP(201人/hm2)和夜间有人区域的平均人口密度nP(214人/hm2)为阈值,将中心城区划分为4种类型:昼夜均高(dP>dP & nP>nP)、昼高夜低(dP>dP & nP < nP)、昼低夜高(dP < dP & nP>nP)和昼夜均低(dP < dP & nP < nP)。统计结果见表 4,空间分布如图 9所示。
| 类型区域 | 面积/km2 | 面积占比/(%) |
| 昼夜均高 | 59.79 | 8.59 |
| 昼高夜低 | 38.28 | 5.50 |
| 昼低夜高 | 41.73 | 6.00 |
| 昼夜均低 | 136.60 | 19.63 |
| 注:面积占比为与中心城区总面积的比例。 | ||

|
| 图 9 中心城区昼夜人口分布模式 Fig. 9 Population distribution difference pattern between daytime and nighttime in central urban area |
图 9显示,昼夜均高类型区域主要分布在两江(长江、汉江)交汇区、长江沿岸江岸段等城市中心区域,这些地区的教育、就业、文化及公共服务配套优势较突出;昼高夜低型主要分布在江汉区、江岸区二环线附近以及东湖风景区和东湖经济开发区等区域,这种类型多对应“候鸟式工作”,即工作后离开;昼低夜高主要分布在青山区及城市外围地区(二、三环之间),这些地区的教育、就业不突出,由于城市开发带来的相对低价住房吸引了大量的城市人口居住在此,形成新的城市生长点。昼夜均低型则主要分布在主城边缘区域(三环外),占中心城区总面积的19.63%,在4种类型中分布面积最大,多为城乡结合部,人口流动性较差。
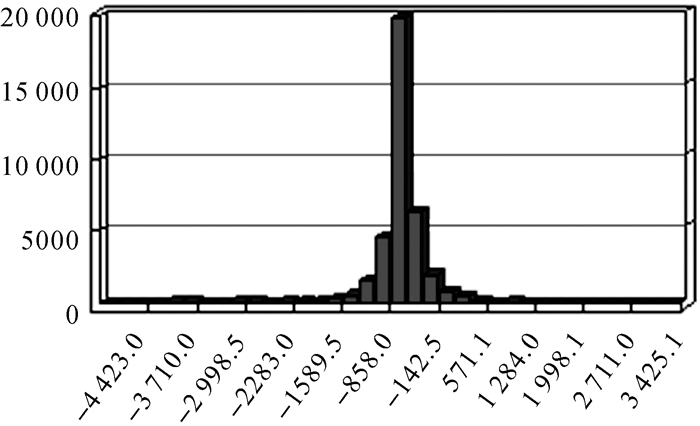
人口昼夜间的变化量dP-nP越大说明白天人口主导能力越强,越小说明夜间人口主导能力越强,0表示昼夜人口数量平衡。从变化量的数据分布来看,差值主要集中在[-800, 800]之间(图 10),空间分布如图 11所示。
|
| 图 10 研究区昼夜人口密度差异统计 Fig. 10 Statistics on population density variation between daytime and nighttime in the study area |

|
| 图 11 研究区昼夜人口密度差异分布模式 Fig. 11 Distribution pattern of population density difference between daytime and nighttime in the study area |
对昼夜人口变化的空间分布进行归纳,发现5种分布模式:①交通线模式,这种模式沿中心城区的重要道路分布,是城市昼夜人口分布差异最大的一种模式,反映了城市交通人口的变化远大于因为工作、外出等形成的人口分布差。②三明治模式,这种模式主要表现为“昼高夜低”和“昼低夜高”层状交替出现。③光晕模式,这种模式主要表现为以“昼高夜低”为中心(环状或片带状)逐渐过渡到“昼低夜高”。④椒盐模式,这种模式主要表现在一定范围内(通常是小范围)“昼高夜低”和“昼低夜高”呈椒盐分布,这种分布其中一个重要原因源自城市发展沿革,在我国的计划经济时代存在的一种城市空间结构——一个大的单位实体内办公区和生活区集中在一起,俗称“前厂后家”。当前多集中在城市老工业区。⑤单体模式,这种模式主要表现为昼夜人口波动不大,多出现在中心城区周边及其远郊乡村,这些地区的人口流动性较差,白天人口在农田或工厂生产作业,夜晚聚集在居民区及附近,地区人口总量变化不大,也反映出人口数量较低的城市边缘区域的人口流动性也低。
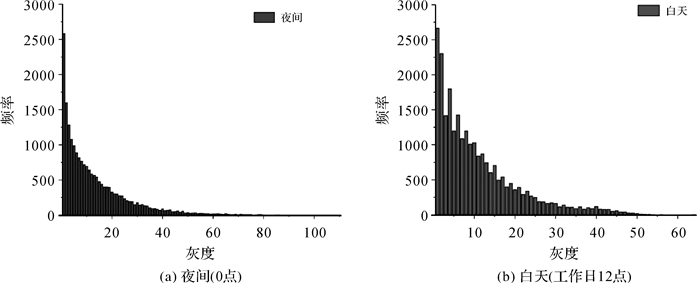
3.4 昼夜人口统计特征人口的空间分布规律一直是城市地理学研究的重点,代表性成果是城市标度律,包括Clark、Tanner、Sherratt、Smeed等模型[35-38],反映了人口数量与空间距离的关系。目前尚未见人口密度与分布面积关系的研究。本文中频率表示统计单元出现的次数,规则格网面积相同,故频率与分布面积为线性关系。昼夜人口密度与频率关系的统计直方图如图 12所示。
|
| 注:横坐标22.139人/灰度单位。 图 12 昼夜人口集聚的灰度—频率直方图 Fig. 12 Grayscale-frequency histogram of daytime and nighttime population agglomeration |
图 12显示,昼夜人口的灰度-频率关系呈单调递减。在显著性水平α=0.05下进行函数拟合,并进行F检验以及赤池信息量(AIC)、贝叶斯信息量(BIC)检验。参数估计及检验结果见表 5、表 6所示。
| 模型名称 | 表达式 | a | b | c | R2 | F1值 | AIC | BIC |
| Compound | a×bx | 2 544.867 61 | 0.906 57 | - | 0.966 93 | 1 334.180 67 | 563.807 28 | 569.661 74 |
| Clark | a×ebx | 2 544.748 45 | -0.098 07 | - | 0.966 93 | 1 334.180 67 | 563.807 28 | 569.661 74 |
| Asymptotic1 | a-b×cx | 22.216 45 | -2 553.211 22 | 0.903 03 | 0.968 07 | 952.718 28 | 597.939 5 | 605.897 06 |
| Smeed(Power) | a×xb | 3 229.502 39 | -0.698 71 | - | 0.853 06 | 286.155 76 | 694.398 8 | 700.475 44 |
| Logarithmic | a+b×ln x | 2 365.832 35 | -615.345 22 | - | 0.945 16 | 818.707 25 | 631.326 87 | 637.403 52 |
| ExpDec1 | a×e-x/b+c | 2 553.211 29 | 9.804 05 | 22.216 47 | 0.968 07 | 952.718 28 | 597.939 5 | 605.897 06 |
| Inverse |

|
135.791 41 | 256.910 42 | 0.742 54 | 150.005 96 | 730.294 03 | 736.370 68 |
| 模型名称 | 表达式 | a | b | c | R2 | F1值 | AIC | BIC |
| Compound | a×bx | 2 037.958 72 | 0.902 23 | 0.935 93 | 1 011.701 99 | 1 005.558 34 | 1 013.433 36 | |
| Clark | a×ebx | 2 037.958 58 | -0.102 89 | 0.935 93 | 1 011.701 99 | 1 005.558 34 | 1 013.433 36 | |
| Asymptotic1 | a-b×cx | 29.548 83 | -2 072.799 11 | 0.894 5 | 0.938 31 | 683.306 91 | 1 001.781 3 | 1 012.202 27 |
| Smeed(Power) | a×xb | 2 819.471 31 | -0.781 83 | 0.924 91 | 855.242 36 | 1 023.023 85 | 1 030.898 87 | |
| Logarithmic | a+b×ln x | 1 571.888 54 | -371.148 64 | 0.852 61 | 409.245 51 | 1 097.202 84 | 1 105.077 87 | |
| ExpDec1 | a×e-x/b+c | 2 070.801 3 | 8.969 6 | 27.809 05 | 0.938 73 | 707.221 05 | 1 001.781 3 | 1 012.202 27 |
| Inverse |
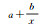
|
38.972 4 | 3 091.501 47 | 0.863 08 | 444.664 46 | 1 089.098 45 | 1 096.973 48 |
从R2、F1值、AIC和BIC分析,上述数学模型的拟合效果均较好,除Inverse模型的R2稍低,其他模型的R2均大于0.85,多数超过0.9。其中,Clark模型的拟合效果最好,拟合系数分别达到0.966 93和0.935 93,拟合效果如图 13所示。对研究区“人口密度—面积”关系提出如下Clark模型
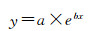 (7)
(7)
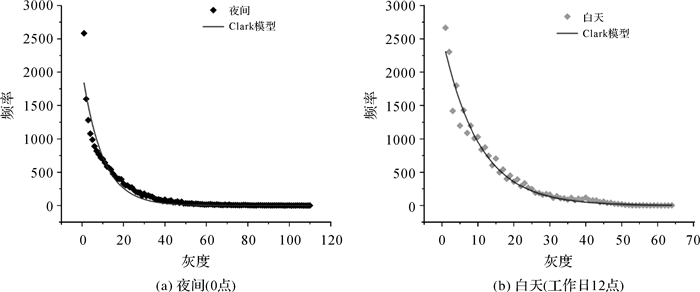
|
| 注:横坐标反映人口密度值,22.139人/灰度单位。纵坐标为该灰度的格网数量,对应面积。 图 13 研究区人口密度-频率的Clark函数拟合 Fig. 13 Clark model fitting result for population density-frequency in the study area |
式中,y为频率;自变量x为人口密度。模型指出,当b < 0,人口密度x出现的频率(地表面积)与x负相关,呈指数衰减。对研究区来说,参数a的值从白天的2 544.748 45下降到夜间的2 037.958 58,参数b的值从白天的-0.098 07下降到夜间的-0.102 89。
3.5 误差分析从模型误差、抽样对比和与其他研究成果对比3个方面分析误差。
(1) 模型误差分析。白天人口空间化主要基于heatmap数据。理想的heatmap能有效地反映人口的空间分布,但有两个原因使得heatmap与真实人口分布还是有一些差异,一个原因是采样时刻人口涌动造成的随机噪声。从人口涌动造成的随机噪声来看,多图像平均法虽然可以降低噪声,但从融合后的图像方差来看
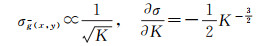 (8)
(8)
式中,σg(x, y)表示融合后的图像方差;K表示参与融合的图像数量。随着K值的增大,σ降低的幅度越来越小,仅通过提高K值作用有限。
另一个原因与heatmap数据的表示方法有关。与绝大多数遥感数据一样,heatmap数据存在像素发散问题。有鉴于此,借鉴文献[39]提出的真实人口分布思想,本文提出真实人口分布误差,定义为人口不可能分布区域的人口计算值与区域总人口的比值。对影像数据表示为
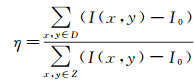 (9)
(9)
式中,I(x, y)为图像(x, y)处的灰度;I0为背景灰度;D为存在逻辑性错误的区域(如人口不可能分布于水域);Z为研究区。将白天人口空间化结果叠加地表覆盖数据,计算其真实人口分布误差η为0.014%。
(2) 抽样对比。抽样对比是常用的数据验证方法,即从结果中抽取部分样本与调查数据进行比对。本文人口计算采用的调查源数据为社区统计数据,也就是说夜间人口空间化结果与社区调查数据一致。社区则是我国当前人口调查的最小尺度地理单元。
(3) 与其他研究成果特征分析对比。文献[40]指出居民住宅类建筑的平均人口密度为0.012 71~0.044 48人/m2。本文中居民住宅类建筑的平均人口密度为0.020 78人/m2。文献[41]对工作日期间建筑对人口的吸引力进了评估,表 7为结果比对。
| 建筑类型 | 建筑对人口吸引力(已有成果) | 本文计算结果 | |||
| 12:00 | 0:00 | 12:00 | 0:00 | ||
| 居住类建筑 | 0.1~0.2 | 1.0 | 0.13 | 1.0 | |
| 商业类建筑 | 0.2~0.3 | 0.0 | 0.29 | 0.0 | |
| 办公服务类建筑 | 0.5~1.0 | 0.0 | 0.87 | 0.0 | |
| 注:建筑对人口吸引力为该类建筑内的人数与该时刻区域内总人数的比值。 | |||||
由表 7可知:①在工作日白天,办公服务类建筑的人口吸引力远大于商业类建筑和居住类建筑,体现了白天城市居民的生产生活状态;②在夜间,居住类建筑的人口吸引力远大于商业类和办公服务类建筑,体现了夜间城市居民的休息状态;③本文的计算结果符合已有研究的数据范围。
4 结论与讨论人们每天穿行在城市不同功能空间的通勤、休憩、消费等行为引发了城市人口集聚的时空差异。由于缺乏先进的技术手段,往往无法真实地记录和量测城市人口的个体流动与整体趋势,人们对城市昼夜人口空间集聚这种城市微观行为的了解仍然十分有限。本文基于城市人群的时间地理特征,从城市大数据中挖掘并模拟城市人群社会时空行为,在此基础上计算城市昼夜人口集聚时空分布。对研究区试验结果的分析显示,昼夜人口密度与面积关系满足城市标度率,幂律特征更符合Clark模型,昼夜时态仅影响模型参数,不影响幂律性。
从昼夜人口空间分布来看,研究区夜间人口较白天人口分布更为集聚、密度变化梯度更大。相对靠拢的昼夜人口重心显示中心城区并非纯粹的商业区,其间也夹杂着相当数量的居住区,中心城区人口流动主要以内部流动为主。城市人口昼夜分布差异归纳出5种形态:交通线模式、三明治模式、光晕模式、椒盐模式和单体模式。这些模式与城市演化及功能空间格局有密切关系,其中交通线模式的人口昼夜分布差异最大。本文提出了一种频率域方法分析人口分布梯度,采用傅里叶变换分析图像的梯度变化、能量分布与共轭性特征,有效揭示人口空间分布的主方向和延伸程度,揭示出武汉中心城区人口分布呈现山水十字轴特征。
本文的研究仍有待进一步完善,一方面城市人口行为受当地气候、文化、风俗的影响,在时间节点上可能略有差异;另一方面,本文所计算的结果依然属于一段时间范围内的统计值,并非实时值。本文采用heatmap数据估算白天的人口分布,不可避免地包含了临时过境人口和周边城市通勤人口等非本地人口,后续研究中有必要进一步清洗数据。
| [1] |
JHAMBA T, JURAN S, JONES M, et al. UNFPA strategy for the 2020 round of population and housing censuses (2015—2024)[J]. Statistical Journal of the IAOS, 2020, 36(1): 43-50. DOI:10.3233/SJI-190600 |
| [2] |
陆杰华. 人口负增长时代: 特征、风险及其应对策略[J]. 社会发展研究, 2019, 6(1): 21-32, 242. LU Jiehua. The era of negative population growth: characteristics, risks and strategies[J]. Journal of Social Development, 2019, 6(1): 21-32, 242. |
| [3] |
ZHAO Qing, PEPE A, DEVLIN A, et al. Impact of Sea-Level-Rise and human activities in coastal regions: an overview[J]. Journal of Geodesy and Geoinformation Science, 2021, 4(1): 124-143. |
| [4] |
WIRTH L. Urbanism as a way of life[M]. Chicago: Chicago University Press, 1964.
|
| [5] |
WU Shuosheng, QIU Xiaomin, WANG Le. Population estimation methods in GIS and remote sensing: a review[J]. GIScience & Remote Sensing, 2005, 42(1): 80-96. |
| [6] |
李素, 庄大方. 基于RS和GIS的人口估计方法研究综述[J]. 地理科学进展, 2006, 25(1): 109-121. LI Su, ZHUANG Dafang. A review on RS- and GIS-based population estimation methods[J]. Progress in Geography, 2006, 25(1): 109-121. DOI:10.3969/j.issn.1007-6301.2006.01.012 |
| [7] |
冯甜甜. 基于高分辨率遥感数据的城市精细尺度人口估算研究[D]. 武汉: 武汉大学, 2010. FENG Tiantian. Urban small area population estimation based on high-resolution remote sensing data[D]. Wuhan: Wuhan University, 2010. |
| [8] |
FISHER P F, LANGFORD M. Modelling the errors in areal interpolation between zonal systems by Monte Carlo simulation[J]. Environment and Planning A: Economy and Space, 1995, 27(2): 211-224. DOI:10.1068/a270211 |
| [9] |
LANGFORD M. Obtaining population estimates in non-census reporting zones: an evaluation of the 3-class dasymetric method[J]. Computers, Environment and Urban Systems, 2006, 30(2): 161-180. DOI:10.1016/j.compenvurbsys.2004.07.001 |
| [10] |
NORBECK S. The law of allometric growth[M]. Michigan: University of Michigan, 1965.
|
| [11] |
HARDIN P J, JACKSON M W, JENSEN R R. Modelling housing unit density from land cover metrics: a Midwestern US example[J]. Geocarto International, 2008, 23(5): 393-411. DOI:10.1080/10106040801950344 |
| [12] |
LO C P. Population estimation using geographically weighted regression[J]. GIScience & Remote Sensing, 2008, 45(2): 131-148. |
| [13] |
ZHANG Junlin, XU Wei, QIN Lianjie, et al. Spatial distribution estimates of the urban population using DSM and DEM data in China[J]. ISPRS International Journal of Geo-Information, 2018, 7(11): 435. DOI:10.3390/ijgi7110435 |
| [14] |
LI Guiying, WENG Qihao. Fine-scale population estimation: how Landsat ETM+ imagery can improve population distribution mapping[J]. Canadian Journal of Remote Sensing, 2010, 36(3): 155-165. DOI:10.5589/m10-035 |
| [15] |
BAKILLAH M, LIANG S, MOBASHERI A, et al. Fine-resolution population mapping using OpenStreetMap points-of-interest[J]. International Journal of Geographical Information Science, 2014, 28(9): 1940-1963. DOI:10.1080/13658816.2014.909045 |
| [16] |
卓莉, 黄信锐, 陶海燕, 等. 基于多智能体模型与建筑物信息的高空间分辨率人口分布模拟[J]. 地理研究, 2014, 33(3): 520-531. ZHUO Li, HUANG Xinrui, TAO Haiyan, et al. High spatial resolution population distribution simulation based on building information and multi-agent[J]. Geographical Research, 2014, 33(3): 520-531. |
| [17] |
LI Xiaoma, ZHOU Weiqi. Dasymetric mapping of urban population in China based on radiance corrected DMSP-OLS nighttime light and land cover data[J]. Science of the Total Environment, 2018, 643: 1248-1256. DOI:10.1016/j.scitotenv.2018.06.244 |
| [18] |
SUN Weichao, ZHANG Xia, WANG Nan, et al. Estimating population density using DMSP-OLS night-time imagery and land cover data[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(6): 2674-2684. DOI:10.1109/JSTARS.2017.2703878 |
| [19] |
戚伟, 李颖, 刘盛和, 等. 城市昼夜人口空间分布的估算及其特征: 以北京市海淀区为例[J]. 地理学报, 2013, 68(10): 1344-1356. QI Wei, LI Ying, LIU Shenghe, et al. Estimation of urban population at daytime and nighttime and analyses of their spatial pattern: a case study of Haidian District, Beijing[J]. Acta Geographica Sinica, 2013, 68(10): 1344-1356. DOI:10.11821/dlxb201310004 |
| [20] |
江晴晴. 城市昼夜人口空间分布模拟方法: 以南京市建邺区为例[D]. 南京: 东南大学, 2015. JIANG Qingqing. Modeling spatial distribution of urban population at daytime and nighttime: a case study of Jianye district, Nanjing[D]. Nanjing: Southeast University, 2015. |
| [21] |
罗阳欢, 祝善友, 张桂欣, 等. 南京市秦淮区昼夜人口空间分布估算与分析[J]. 长江流域资源与环境, 2018, 27(5): 1020-1030. LUO Yanghuan, ZHU Shanyou, ZHANG Guixin, et al. Estimation and analysis of spatial distribution of urban population during the daytime and nighttime in Qinhuai district of Nanjing[J]. Resources and Environment in the Yangtze Basin, 2018, 27(5): 1020-1030. |
| [22] |
杨松. 基于建筑空间的城市昼夜人口时空分布研究[D]. 成都: 西南石油大学, 2019. YANG Song. Study on spatial and temporal distribution of urban day and night population based on architectural space[D]. Chengdu: Southwest Petroleum University, 2019. |
| [23] |
陈慕琳. 基于互联网挖掘信息及建筑数据估算的精细尺度昼夜人口空间格局分析[D]. 武汉: 华中师范大学, 2019. CHEN Mulin. Spatial distribution analysis of fine scale daytime and nighttime population based on the Internet mining information and building data estimation[D]. Wuhan: Central China Normal University, 2019. |
| [24] |
NEME |
| [25] |
武汉市统计局. 武汉统计年鉴(2018)[M]. 北京: 中国统计出版社, 2019. Wuhan Municipal Bureau of Statistics. Wuhan Statistical Yearbook(2018)[M]. Beijing: China Statistics Press, 2019. |
| [26] |
BOEING G. Estimating local daytime population density from census and payroll data[J]. Regional Studies, Regional Science, 2018, 5(1): 179-182. DOI:10.1080/21681376.2018.1455535 |
| [27] |
罗名海, 刘艳芳, 詹庆明, 等. 武汉市地理国情监测与城市协调发展研究: 2019[M]. 北京: 测绘出版社, 2019. LUO Minghai, LIU Yanfang, ZHAN Qingming, et al. Wuhan city geographical national conditions monitoring and urban coordinated development research: 2019[M]. Beijing: Surveying and Mapping Press, 2019. |
| [28] |
极光大数据. 2018年中国城市通勤研究报告[R]. 深圳: 极光大数据, 2019. Aurora Big Data. 2018 China Urban Commuter Research Report[R]. Shenzhen: Aurora Big Data, 2019. |
| [29] |
COX K R, GOLLEDGE R G. Behavioral problems in geography: a symposium[D]. Evanston: Northwestern University Press, 1969.
|
| [30] |
ORBAN K, EDBERG A K, ERLANDSSON L K. Using a time-geographical diary method in order to facilitate reflections on changes in patterns of daily occupations[J]. Scandinavian Journal of Occupational Therapy, 2012, 19(3): 249-259. DOI:10.3109/11038128.2011.620981 |
| [31] |
李燕, 张艳艳. 城乡青少年智能手机使用现状调查与分析[J]. 济宁学院学报, 2020, 41(5): 60-65. LI Yan, ZHANG Yanyan. Survey and analysis of the current situation of the use of smart-phone by urban and rural adolescents[J]. Journal of Jining University, 2020, 41(5): 60-65. |
| [32] |
柴祥德. 中小学生使用智能手机现象及学校管理思考[J]. 数字教育, 2016, 2(3): 69-72. CHAI Xiangde. Thoughts on the phenomenon of primary and secondary school students' using smart phones and school management[J]. Digital Education, 2016, 2(3): 69-72. |
| [33] |
BELLONE F, CUNNINGHAM R. All roads lead to center Laxton[J]. Journal of Economic Integration, 1993, 13(3): 47-52. |
| [34] |
白雪. 1984―2013年中国经济重心、人口重心轨迹演变及机制探讨[J]. 热带地理, 2015, 35(5): 762-769. BAI Xue. Evolution and mechanism of economic and population gravity center in China during 1984—2013[J]. Tropical Geography, 2015, 35(5): 762-769. |
| [35] |
CLARK C. Urban population densities[J]. Journal of the Royal Statistical Society Series A (General), 1951, 114(4): 490. |
| [36] |
TANNER J C. Factors affecting the amount of travel[M]. London: H. M. Stationery Office, 1961.
|
| [37] |
SHERRATT G G. A model for general urban growth[M]. Oxford: Pergamon Press, 1960.
|
| [38] |
NEWLING B. The spatial variation of urban population densities[J]. Geographical Review, 1969, 59: 242-252. |
| [39] |
吕安民, 李成名, 林宗坚, 等. 人口密度的空间连续分布模型[J]. 测绘学报, 2003, 32(4): 344-348. LÜ Anmin, LI Chengming, LIN Zongjian, et al. Spatial continuous surface model of population density[J]. Acta Geodaetica et Cartographic Sinica, 2003, 32(4): 344-348. |
| [40] |
王冰. 基于遥感和GIS的高分辨率城市人口密度模拟: 以重庆市北碚城区为例[D]. 重庆: 西南大学, 2010. WANG Bing. Simulation of high-resolution urban population density based on remote sensing and GIS: a case study in Beibei District, Chongqing[D]. Chongqing: Southwest University, 2010. |
| [41] |
张子民, 周英, 李琦, 等. 城市局域动态人口估算方法与模拟应用[J]. 地球信息科学学报, 2010, 12(4): 503-509. ZHANG Zimin, ZHOU Ying, LI Qi, et al. An estimation method of dynamic population within an urban local area[J]. Journal of Geo-Information Science, 2010, 12(4): 503-509. |



