2. 航天飞行动力学技术重点实验室, 北京 100094;
3. 北京跟跟与通信技术研究所, 北京 100094
2. Science and Technology on Aerospace Flight Dynamics Laboratory, Beijing 100094, China;
3. Beijing Institute of Tracking and Telecommunications Technology, Beijing 100094, China
深空无线电测量的观测类型主要有测速、测距、甚长基线干涉测量(very long baseline interfero-metry, VLBI)等[1]。在深空探测任务中,测速主要通过多普勒测速予以实现,利用多普勒效应测量深空探测器与观测站之间收发频率的变化获取深空探测器相对于测站的视向速度。多普勒测速系统按测量方式一般分为单向测速、双向测速和三向测速,按积分方式不同又分为瞬时多普勒和积分多普勒。瞬时多普勒测速原理与积分多普勒的测速原理相同,只是积分周期较短(如0.2 s),双向多普勒测速可以看作三向多普勒测速的特例,三向多普勒上行测站和下行测站相同时即为双向多普勒[2]。
单向多普勒测速作为深空探测中一种经济有效的测量方式,其优点是无须上行链路,只需要测站接收卫星发射的下行信号,该测量方式节省资源消耗,更容易实现遥远距离的深空测量[3]。缺点在于需要探测器提供高稳定度的频率输出,随着探测器高稳定度频标的使用,单向多普勒跟踪数据的重要性日渐突出[4]。
对于深空探测,使用短稳为1×10-12/s的超稳振荡器(ultra-stable oscillator, USO)提供导航服务可满足1.5 km星历重建需求,若想实现多普勒最佳导航性能,USO短稳必须优于1×10-13/s[5-6]。美国1973年发射的Pioneer11,其星上频率源的稳定度为10-10,单向多普勒测速的噪声为0.506 mm/s (频率噪声为0.015 Hz),是双向多普勒测速噪声水平的3倍[7]。美国2011年发射的Mars Science Laboratory(MSL)使用单向测速、双向测速、双向测距及ΔDOR多种测量方式进行测量,其中USO短稳精度为1×10-12/s,单向测速的噪声为0.5 mm/s(60 s),同时双向测速的精度为0.03 mm/s(60 s)[8]。中国首个火星探测器“萤火一号”设计使用单向开环测量和VLBI测量接收探测器发射的下行无线电信号,USO的短期稳定度为1×10-12/s,测速噪声预计0.3 mm/s[9-10]。
“天问一号”(Tianwen-1,TW01)任务是我国行星探测的首次任务,通过一次任务实现了火星“环绕”“着陆”“巡视”的3步跨越。任务主要采用双向多普勒测速,同时验证单向多普勒测速技术[11]。任务中利用单向多普勒进行轨道确定是我国深空探测任务中的首次实际应用,本文使用TW01中继段单向多普勒进行轨道计算,并利用双向测量+VLBI数据解算的轨道进行验证。相关处理策略与结论可以直接应用于TW01后续阶段飞行任务,也可为我国未来其他深空探测任务提供借鉴。
1 单向多普勒建模与误差分析单向多普勒测速不需要地面站发射上行信号,直接接收星载下行频率信号,将接收机接收频率与星载下行频率进行比对,计算得到两者的相对速度[12]。
星载频率源的稳定度和接收机的热噪声引起的误差为随机误差,而频率源的准确度、电波传播等因素引起的误差为系统误差。为了掌握各误差源引入的测速误差量级,本文在建立单向多普勒观测量计算模型和偏导数的基础上,详细分析了各误差源引入的测速误差大小。
1.1 单向多普勒观测量计算模型及偏导数单向多普勒观测量为测站的接收频率,对单向多普勒进行建模,得到接收频率对探测器位置和发射频率的偏导数。
1.1.1 接收频率对探测器位置偏导数单向多普勒的表达式为[13]
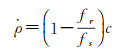 (1)
(1)
式中,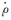
对于积分多普勒
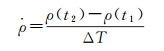 (2)
(2)
式中,ρ(t1)、ρ(t2)分别为积分开始和结束时刻探测器相对于测站的距离;ΔT为积分周期。接收频率对位置的偏导数为[14]
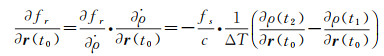 (3)
(3)
式中,ρ的计算需要考虑光行时迭代,假设数据时标为信号的接收时刻,则
 (4)
(4)
式中,R(tR)、r(tS)分别表示信号接收时刻测站位置以及对应发射时刻探测器插值星历,其中
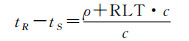 (5)
(5)
RLT为相对论光行时,根据探测器和地面站的位置矢量计算
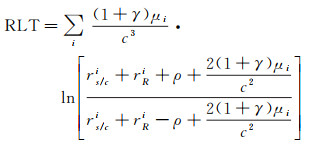 (6)
(6)
式中,i代表太阳系中某个天体;rs/ci表示探测器到天体i质心距离;rRi表示测站到天体i质心距离;μi为天体i引力常数,在火星任务中主要考虑太阳的影响。
1.1.2 接收频率对发射信号的偏导数根据式(1),可以计算接收频率对发射频率的偏导数为
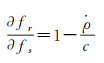 (7)
(7)
探测器相对于测站的速度为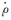
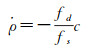 (8)
(8)
单向测速误差为
 (9)
(9)
式中,σV为单向测速的标准差;σf为频率的标准差。单向多普勒测速的测量误差源主要有接收机处的热噪声、来自探测器上的频率源的相位噪声及下行链路载波通过日冕时获取的相位闪烁,单向多普勒测量的误差方差σV2可以建模为
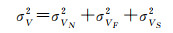 (10)
(10)
式中,σVN2、σVF2和σVS2分别表示接收机处的热噪声、频率源的相位噪声,以及来自太阳的相位闪烁噪声。σVN2和σVF2属于测量产生的随机误差,σVS2是测量产生的系统误差。除了测量误差,星载频率源fs自身的准确度也会使测速存在系统误差[15],下文将分别进行分析。此外,由电离层、对流层和多路径等电波传播引入的测速误差需利用相应的数据处理方法进行修正,这里不再赘述。
1.2.1 随机误差分析 1.2.1.1 接收机热噪声测速信号载波相位受接收机热噪声影响产生随机误差,对于二阶锁相环路,频偏热噪声误差σVN2可以表示为[16-17]
 (11)
(11)
其中
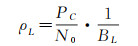 (12)
(12)
式中,PC/N0为下行信号的功率谱密度;BL为单边环路带宽。TW01测控和数传模式使用不同调制方式,在测控模式下主要使用残留边带调制,在数传模式下主要使用抑制载波调制,不同模式使用的星载天线也不同。测控模式下对地主要使用高增益天线,数传模式主要使用中增益天线。另外,调制度、信号传输速率等多种因素导致下行信号的信噪比变化较大。本文分析的TW01单向多普勒信号大多在测控模式下获取的,按照式(11)计算预估,对应接收机热噪声造成的测速误差大约为±0.02 mm/s。
1.2.1.2 频率源稳定度引入误差对于单向测速系统,这部分误差主要包括星上频率源和地面接收机的频率标准源的频率稳定度。由于地面接收机使用的都是频率稳定度较高的铷原子钟或氢原子钟,引入误差较小,这里主要考虑星上频率源的频率稳定度对测速造成的误差。深空中频率源稳定度引入误差σVF的计算公式近似为
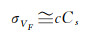 (13)
(13)
式中,Cs表示振荡器的稳定度,用阿伦方差来表示。由于体积、质量和功耗等的限制,TW01探测器发射机采用高稳恒温晶振,频率短期稳定度为1×10-12/s,长期稳定度为1×10-10/d。根据式(13),可以估算出星上频率源稳定度造成的测速误差约为±0.3 mm/s。根据文献[10]的相关测试,若连续测量弧段持续8 h以上,此时的Cs将小于1×10-11,则该时段由于频率不稳定度引起的偏差可以达到±3 mm/s。
1.2.2 系统误差 1.2.2.1 太阳相位闪烁误差载波通过日冕时会产生相位闪烁,这给多普勒测速带来了随机误差。相位闪烁对多普勒测速误差σVS2取决于太阳-地球-探测器(Sun-Earth-probe, SEP)角度、载波频率和积分时间,σVS2近似值为[18]
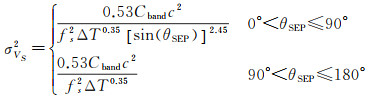 (14)
(14)
式中,θSEP为太阳-地球-探测器角度;Cband为常值,由发射频率决定
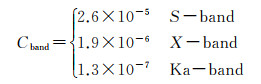 (15)
(15)
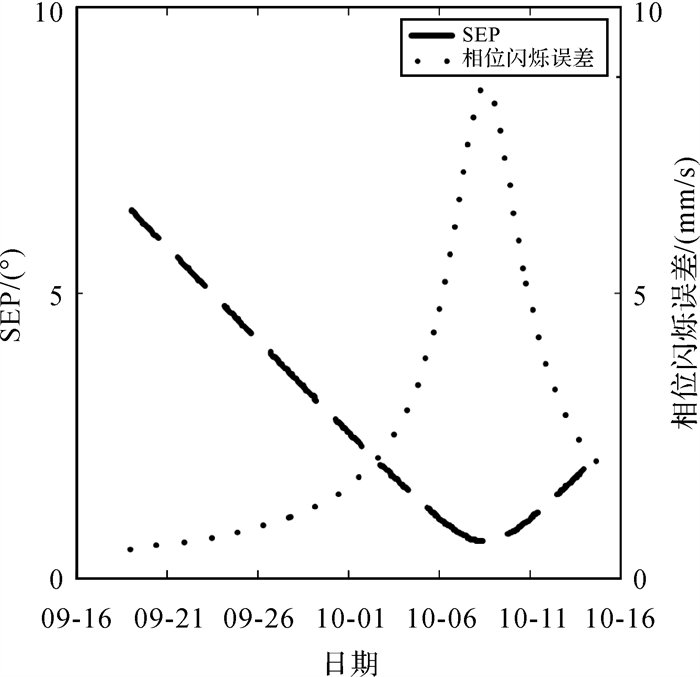
统计2021年9月16日至2021年10月16日TW01探测器的SEP角,计算太阳相位闪烁误差,结果如图 1所示,随着SEP角度的减小,太阳相位闪烁误差从1 mm/s快速增加至9 mm/s。
|
| 图 1 SEP变化和相位闪烁误差 Fig. 1 SEP and phase scintillation error |
1.2.2.2 频率准确度影响
单向多普勒不同于双向多普勒最主要的误差是频率准确度引起的系统误差。由于直接使用星上频率源发射频率,根据式(7),频率偏移会引起多普勒测速的系统性误差,该系统性误差为非线性常值,与测站的视向速度成正比。系统差表示为
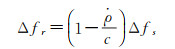
由于TW01星载信频率源精度较差,指标值为±5×10-6,根据式(9)计算,对应的发射频率误差最大为±42 MHz,测速误差最大值为±150 m/s,实际测得的误差为±20 m/s左右。
综上,接收机处的热噪声造成的测速误差为±0.02 mm/s,频率的不稳定度对应单向测速的误差为±0.32 mm/s,可以支持工程定轨。日凌期间,由于SEP角变小,测速误差明显增大,这一误差将直接影响定轨结果。频率准确度产生较大的系统误差,在定轨过程中需要将该误差作为系统误差进行解算[19]。
2 TW01单向多普勒数据计算分析 2.1 任务概况TW01的测控主要由中国深空测控网(Chinese Deep Space Network, CDSN)来完成,CNSN主要由喀什(35 m)、佳木斯(66 m)和南美洲的阿根廷(35 m)3个深空站组成[20-21]。环绕器测控数传设备主要由2副低增益接收天线、2副低增益发射天线、1副中增益发射天线、1副高增益天线、2台深空应答机、2台行波管放大器、1台固态功率放大器、微波网络、射频线缆和波导等组成[22]。根据环绕器测控数传分系统工作模式的不同,使用不同的工作设备。环绕器处于数传模式、轨控前后、日凌期间及安全模式下应答机为非相干状态,单向多普勒测速数据主要是在该状态下获取的,另外,由于深空测量的时延较大,双向测速链路建立前,测站按测控计划已建立接收下行信号的状态,此时收到的也为单向多普勒数据。
2.2 轨道计算策略本文选取单向多普勒数据覆盖较好,动量轮卸载频率相对较少的两段中继轨道数据进行分析。第1段时间为2021年6月4日至2021年6月12日,该弧段主要包括双向测距、双向测速、VLBI和单向多普勒数据。第2段时间为2021年9月24日至2021年10月3日,环绕器进入日凌状态设置,SEP角由5°减小至1°附近,只获取了探测器单向多普勒数据。
使用第1段的双向测距、测速和VLBI数据建立基准轨道[23-24],通过重叠弧段评估基准轨道的精度。轨道解算中考虑的主要计算因素[25-26]见表 1。
| 参数名称 | 参数值 |
| 定轨数据 | 双向测距、双向测速、VLBI、单向多普勒 |
| 定轨弧段/d | 约3 |
| 火星重力场 | JGMRO120 |
| 太阳辐射压模型 | 固定面质比,Cr初值l.2 |
| 行星历表 | JPL DE436 |
| 动量轮卸载模型 | 匀加速度模型(RTN坐标系) |
| 相对论影响 | 考虑 |
| 解算参数 | 位置速度 动量轮卸载 下行频率 |
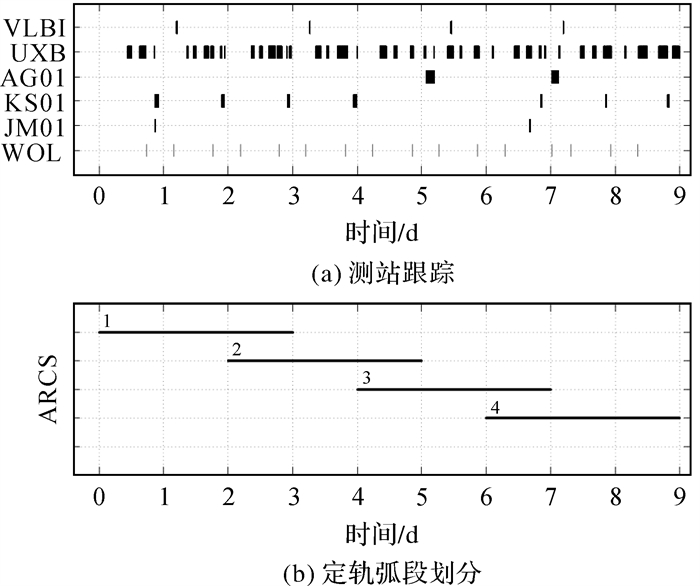
图 2给出第1段数据的测站跟踪和定轨弧段的划分情况,开始时间为2021年6月4日零时。图 2(a)中的UXB和VLBI分别代表双向测距测速和VLBI跟踪数据的覆盖情况,佳木斯深空站(JM01)、喀什深空站(KS01)、阿根廷深空站(AG01)分别表示3个深空站的单向多普勒跟踪弧段,WOL(wheel off-loading)为动量轮卸载的时刻,在轨道计算时需要加入相应力模型进行解算。图 2(b)给出了定轨弧段的划分,ARCS1-4分别表示4组定轨记录,横轴对应时间段为每组定轨计算使用的数据弧段。
|
| 图 2 第1段数据测站跟踪情况和定轨弧段划分 Fig. 2 Tracking data coverage by station and arc segment division in the first section |
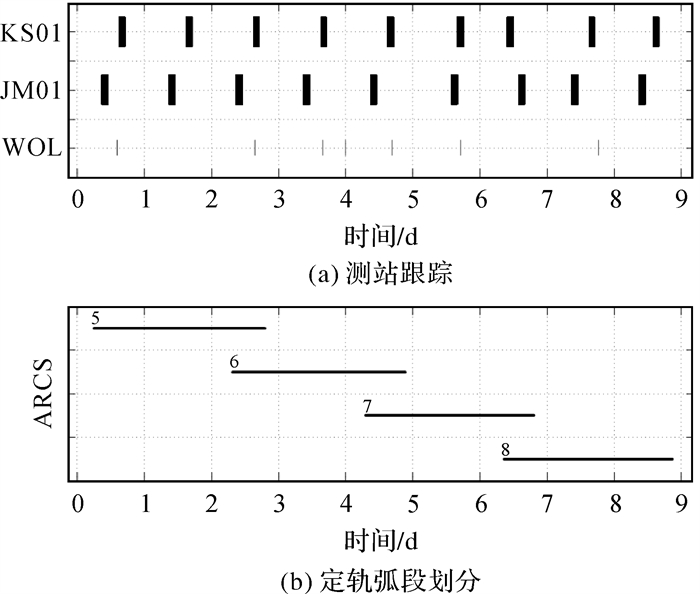
图 3为第2段数据的测站分配和跟踪弧段的划分情况,开始时间为2021年9月24日0时。该段数据中只有喀什和佳木斯2个测站的单向多普勒数据,图 3中同时标注了动量轮卸载的时间,将该时间段数据分成编号为ARCS5-8的4个子弧段进行定轨计算。
|
| 图 3 第2段数据测站跟踪情况和定轨弧段划分 Fig. 3 Tracking data coverage by station and arc segment division in the second section |
本文利用基准轨道评估第1段数据单向多普勒的定轨精度,同时通过重叠弧段验证单向多普勒的轨道精度。
2.3 基准轨道的解算使用第1段的双向测距、测速和VLBI数据建立基准轨道,通过重叠弧段评估基准轨道的精度,定轨残差和重叠弧段的精度见表 2,表中仅给出了双向测速的残差值。
| 子弧段 | 定轨弧段 | 重叠弧段 | ||||||
| 开始时间(MJD) | 结束时间(MJD) | 数据弧长/d | 测速残差/(mm/s) | 数据弧长/d | 位置误差/m | 速度误差/(m/s) | ||
| 1 | 59 369.44 | 59 371.98 | 2.54 | 0.41 | - | - | - | |
| 2 | 59 371.35 | 59 373.87 | 2.52 | 0.42 | 0.63 | 25.06 | 0.015 | |
| 3 | 59 373.00 | 59 375.92 | 2.92 | 0.53 | 0.87 | 35.14 | 0.027 | |
| 4 | 59 375.10 | 59 377.99 | 2.89 | 0.77 | 0.82 | 17.24 | 0.012 | |
| 均值 | - | - | 2.72 | 0.53 | 0.77 | 25.81 | 0.018 | |
双向测距、测速和VLBI数据对环火中继轨道的约束较好,从定轨残差看,测速残差的均值在0.53 mm/s。根据重叠弧段比对的结果可以得到,基准轨道重叠弧段位置误差小于50 m,速度误差小于0.03 m/s。
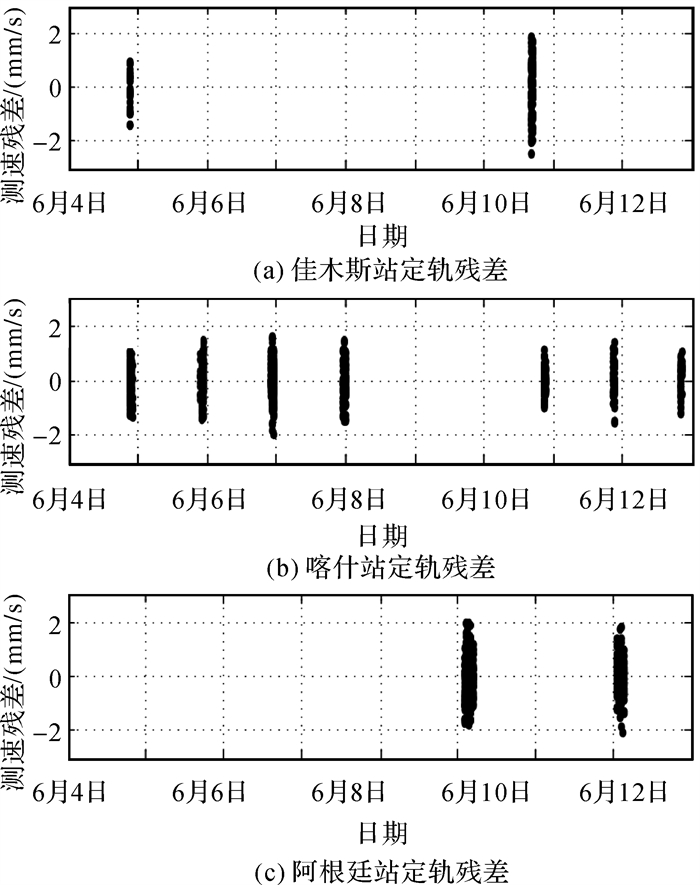
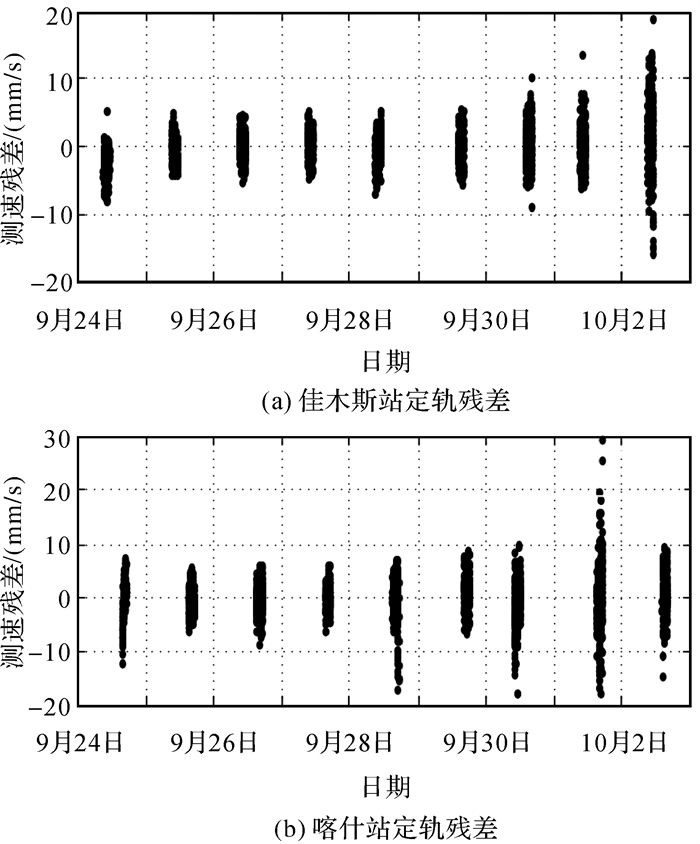
2.4 单向多普勒定轨精度评估 2.4.1 单向多普勒定轨残差本文使用2.1节建立的模型和表 1中的定轨解算参数对两段单向多普勒数据进行定轨计算,两段数据的定轨残差分别如图 4、图 5所示,残差统计结果见表 3。
|
| 图 4 第1段单向多普勒测速残差 Fig. 4 Residual of one-way Doppler in the first section |
|
| 图 5 第2段单向多普勒测速残差 Fig. 5 Residual of one-way Doppler in the first section |
| 子弧段 | 定轨弧段 | 与基准轨道误差 | 重叠弧段 | |||||||||
| 开始时间(MJD) | 结束时间(MJD) | 弧长/d | 测速残差/(mm/s) | 系统误差/(m/s) | 位置误差/m | 速度误差/(m/s) | 弧长/d | 位置误差/m | 速度误差/(m/s) | |||
| 1 | 59 369.87 | 59 371.96 | 2.09 | 0.65 | 20.007 | 924.10 | 0.18 | - | - | - | ||
| 2 | 59 371.92 | 59 372.99 | 1.07 | 0.62 | 20.004 | 518.77 | 0.34 | 0.04 | 927.95 | 0.44 | ||
| 3 | 59 374.07 | 59 375.87 | 1.80 | 0.75 | 19.984 | 585.80 | 0.32 | - | - | - | ||
| 4 | 59 375.67 | 59 377.84 | 2.17 | 0.66 | 20.001 | 450.92 | 0.16 | 0.2 | 321.09 | 0.12 | ||
| 5 | 59 481.37 | 59 483.71 | 2.34 | 2.53 | 20.241 | - | - | - | - | - | ||
| 6 | 59 483.37 | 59 485.71 | 2.34 | 2.13 | 20.245 | - | - | 0.34 | 304.67 | 0.17 | ||
| 7 | 59 485.37 | 59 487.67 | 2.30 | 2.54 | 20.256 | - | - | 0.34 | 552.29 | 0.14 | ||
| 8 | 59 487.41 | 59 489.67 | 2.26 | 3.94 | 20.262 | - | - | 0.26 | 850.00 | 0.61 | ||
由定轨残差和统计结果可知,由于第1段数据(ARCS1-4)时间段的SEP角较大,星载频率源的稳定度是产生误差的主要原因,测速残差RMS为0.67 mm/s左右。在第2段数据(ARCS5-8)时间范围内,环绕器已设置进入日凌状态,星上转发器处于非相干模式,佳木斯和喀什深空站在测控模式下获取单向多普勒数据,2个站每天跟踪时长约2 h,相比于第1段单向多普勒的覆盖时间更长,本文利用大约2.5 d的单向多普勒数据进行轨道确定。从残差统计的结果看,受到SEP夹角逐渐减小的影响,太阳相位闪烁误差的影响显著,测速残差逐渐增大,RMS最大达到了4 mm/s,这与理论误差分析结论一致。
2.4.2 单向多普勒定轨精度对定轨结果进行统计,表 3同时给出解算的系统误差、第1段数据与基准轨道比较结果及两段数据的重叠弧段轨道精度。
由定轨结果可以看出,由于星载振荡器频率的准确度较低,导致单向多普勒解算的下行频率频偏存在约565 Hz的系统差,对应约20.1 m/s的测速系统误差。根据第1段数据(ARCS1-4)定轨结果与基准轨道的比较结果,单向多普勒定轨的位置精度最大为1 km,最小为450 m。通过两段数据重叠弧段的比较,单向多普勒定轨的位置误差小于1 km,速度误差小于0.7 m/s。
3 结论TW01单向多普勒轨道确定是我国深空探测任务中的首次实际应用。本文对单向多普勒开展建模和误差分析,实际误差和理论分析相当,对TW01在中继轨道段单向多普勒定轨计算的能力进行评估,为后续单向多普勒的工程应用提供了参考,主要结论如下:
(1) 星载频率源准确度和稳定度及太阳相位闪烁是单向多普勒测速的主要误差源,星载频率源的长期漂移造成单向多普勒下行频率存在约565 Hz的偏差,太阳相位闪烁对日凌期间多普勒定轨残差影响显著。
(2) 在定轨计算中,考虑动量轮卸载等影响因素条件下,中继轨道段仅使用单向多普勒数据可以实现优于1 km的定轨精度。
| [1] |
MOYER T D. Formulation for observed and computed values of deep space network data types for navigation[M]. Hoboken: Wiley-Interscience, 2003.
|
| [2] |
曹建峰, 黄勇, 胡小工, 等. 深空探测中多普勒的建模与应用[J]. 宇航学报, 2011, 32(7): 1583-1589. CAO Jianfeng, HUANG Yong, HU Xiaogong, et al. Modeling and application of Doppler data in deep space exploration[J]. Journal of Astronautics, 2011, 32(7): 1583-1589. |
| [3] |
简念川, 尚堃, 张素君, 等. 深空探测用数字开环多普勒技术初步研制及其在嫦娥一号探测任务中的应用[J]. 中国科学(G辑: 物理学力学天文学), 2009, 39(10): 1400-1409. JIAN Nianchuan, SHANG Kun, ZHANG Sujun, et al. Preliminary development of digital open-loop Doppler technology for deep space exploration and its application in Chang'e-1 exploration mission[J]. Science in China (Series G: Physics, Mechanics & Astronomy), 2009, 39(10): 1400-1409. |
| [4] |
SHAPIRA A, STERN A, PRAZOT S, et al. An ultra stable oscillator for the 3GM experiment of the JUICE mission[C]//Proceedings of 2016 European Frequency and Time Forum (EFTF). York, UK: IEEE, 2016: 1-5.
|
| [5] |
JOCHIM E F M. On one-way Doppler measurements of space craft and celestial objects[J]. Acta Astronautica, 2010, 66(1/2): 309-330. |
| [6] |
KUGA H K, ORLANDO V. Assessing orbit determination through one way Doppler signals[C]//Proceedings of 2003 International Symposium on Spacecraft Flight Dynamics. Moscow, Russia: [s. n. ], 2003: 1-8.
|
| [7] |
CHAO C C, ONDRASIK V J, SIEGEL H L. A demonstration of differenced dual-station one-way Doppler conducted with Pioneer 11[R]. Pasadena, California: [s. n. ], 1978: 104-110.
|
| [8] |
GROTZINGER J P, CRISP J, VASAVADA A R, et al. Mars science laboratory mission and science investigation[J]. Space Science Reviews, 2012, 170(1): 5-56. |
| [9] |
郭丽莉, 姜亚祥, 谢春坚. 萤火一号火星探测器高稳定频率源设计[J]. 上海航天, 2013, 30(4): 204-206, 254. GUO Lili, JIANG Yaxiang, XIE Chunjian. Design of high-stability crystal source of YH-1 Mars probe[J]. Aerospace Shanghai, 2013, 30(4): 204-206, 254. |
| [10] |
王震, 简念川, 张素君, 等. YH-1星载超稳定晶振的频率稳定性的测试与分析[J]. 中国科学院上海天文台年刊, 2011(1): 69-74. WANG Zhen, JIAN Nianchuan, ZHANG Sujun, et al. Test and analysis of frequency stability of USO in YH-1[J]. Annals of Shanghai Astronomical Observatory Chinese Academy of Sciences, 2011(1): 69-74. |
| [11] |
孙泽洲, 饶炜, 贾阳, 等. "天问一号"火星探测器关键任务系统设计[J]. 空间控制技术与应用, 2021, 47(5): 9-16. SUN Zezhou, RAO Wei, JIA Yang, et al. Key mission system design of Tianwen-1 Mars probe[J]. Aerospace Control and Application, 2021, 47(5): 9-16. |
| [12] |
郑为民, 马茂莉, 王文彬. 深空探测器被动式高精度多普勒测量方法与应用[J]. 宇航学报, 2013, 34(11): 1462-1467. ZHENG Weimin, MA Maoli, WANG Wenbin. High-precision passive Doppler measurement method and its applications in deep space explorater[J]. Journal of Astronautics, 2013, 34(11): 1462-1467. |
| [13] |
曹建峰, 黄勇, 刘磊, 等. 深空探测器三程多普勒建模与算法实现[J]. 宇航学报, 2017, 38(3): 304-309. CAO Jianfeng, HUANG Yong, LIU Lei, et al. Modeling and algorithm realization of three-way Doppler for deep space exploration[J]. Journal of Astronautics, 2017, 38(3): 304-309. |
| [14] |
金炜桐, 李斐, 杨轩, 等. 行星际深空探测中双程测速的高精度计算方法[J]. 武汉大学学报(信息科学版), 2018, 43(10): 1483-1489. JIN Weitong, LI Fei, YANG Xuan, et al. High precision computational method of two-way range-rate in long-distance deep space exploration[J]. Geomatics and Information Science of Wuhan University, 2018, 43(10): 1483-1489. |
| [15] |
LANYI G E, BORDER J S, SHIN D K. Radiometric spacecraft tracking for deep space navigation[C]//Proceedings of 2008 National Technical Meeting of the Institute of Navigation. San Diego, CA, USA: [s. n. ], 2008: 86-90.
|
| [16] |
BORDER J S, LANYI G E, DONG K S. Radiometric tracking for deep space navigation[J]. Advances in the Astronautical Ences, 2008, 131. |
| [17] |
THORNTON C L, BORDER J S. Radiometric tracking techniques for deep-space navigation[M]. New York: John Wiley & Sons, 2003: 22-37.
|
| [18] |
ASMAR S W, ARMSTRONG J W, LESS L, et al. Spacecraft Doppler tracking: noise budget and accuracy achievable in precision radio science observations[J]. Radio Science, 2005, 40(2): 1-9. |
| [19] |
黄磊, 王宏, 樊敏. 三向测量技术在深空探测中的应用研究[J]. 飞行器测控学报, 2012, 31(3): 6-10. HUANG Lei, WANG Hong, FAN Min. Application of three-way measurement in deep space exploration[J]. Journal of Spacecraft TT&C Technology, 2012, 31(3): 6-10. |
| [20] |
董光亮, 李海涛, 郝万宏, 等. 中国深空测控系统建设与技术发展[J]. 深空探测学报, 2018, 5(2): 99-114. DONG Guangliang, LI Haitao, HAO Wanhong, et al. Development and future of China's deep space TT & C system[J]. Journal of Deep Space Exploration, 2018, 5(2): 99-114. |
| [21] |
叶茂, 李斐, 鄢建国, 等. 深空探测器精密定轨与重力场解算系统(WUDOGS)及其应用分析[J]. 测绘学报, 2017, 46(3): 288-296. YE Mao, LI Fei, YAN Jianguo, et al. Wuhan university deep-space orbit determination and gravity recovery system(WUDOGS) and its application analysis[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(3): 288-296. DOI:10.11947/j.AGCS.2017.20160525 |
| [22] |
张荣桥. 中国首次火星探测工程[M]. 北京: 宇航出版社, 2021. ZHANG Rongqiao. China's first Mars exploration pro-gram[M]. Beijing: China Astronautic Publishing House, 2021. |
| [23] |
CHEN L, PING J, CAO J, et al. Retrieving Doppler frequency via local correlation method of segmented modeling[J]. Remote Sensing, 2021, 13(14): 2846. |
| [24] |
鄢建国, 李斐, 平劲松. 基于MGS测图段部分弧段的精密定轨及火星重力场模型解算[J]. 测绘学报, 2010, 39(5): 484-490. YAN Jianguo, LI Fei, PING Jinsong. Precision orbit determination of MGS mapping phase ARCS and Martian gravity field model solution[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 484-490. |
| [25] |
TAPLEY B D, SCHUTZ B E, GEORGE H B. Statistical orbit determination[M]. San Diego: Elsevier Academic Press, 2004.
|
| [26] |
胡松杰, 唐歌实. 北京中心深空探测器精密定轨与分析软件系统[J]. 飞行器测控学报, 2010, 29(5): 69-74. HU Songjie, TANG Geshi. BACC orbit determination and analysis software for deep-space explorers[J]. Journal of Spacecraft TT&C Technology, 2010, 29(5): 69-74. |



