2. 北京空间飞行器总体设计部, 北京 100094;
3. 武汉大学测绘学院, 湖北 武汉 430079
2. Beijing Institute of Spacecraft System Engineering, Beijing 100094, China;
3. School of Geodesy and Geomatics, Wuhan University, Wuhan 43079, China
2021年5月22日,我国首辆火星车“祝融号”成功登陆火星表面。截至2021年8月22日,“祝融号”火星车在火星表面安全行驶了90 d,获取了大量火星表面的图像及探测数据。“祝融号”火星车配备了立体视觉系统。立体视觉系统是“祝融号”火星车的重要工程载荷,由导航相机(A、B)、桅杆机构和惯性测量单元(IMU)构成。导航相机主要用于观察巡视器周围5~7 m范围内的地形环境,并对火星车进行图像定位。导航相机A和导航相机B构成立体相机。导航相机安装在云台上,云台通过桅杆机构与火星车顶板连接。桅杆机构包括3个转动关节,分别是展开关节、偏航关节和俯仰关节。桅杆机构可以带动导航相机A、B以任意的位姿对火星车周围的地形进行感知成像。导航相机设计使用了中等视场、中等焦距的镜头。IMU安装在火星车体内部,用于实时测量火星车的位置与姿态。立体视觉系统在“祝融号”火星车上的安装位置如图 1所示。

|
| 图 1 “祝融号”火星车的立体视觉系统 Fig. 1 Stereo vision system of Zhurong rover |
立体视觉系统主要应用于“祝融号”火星车的遥操作任务,遥操作任务的目的是由地面制定火星车的行驶计划和策略,控制火星车在火星表面安全行驶。立体视觉系统在遥操作任务中起着基础并且重要的作用,主要用于对火星地形环境的感知。然后,基于立体视觉系统获取的序列立体像对及遥测位姿,完成图像定位、视觉测量及地形重建。最后,基于生成的数字地形进行火星车行驶轨迹的规划,从而指导火星车在火星表面安全行驶。
发射前,火星车处于研制阶段,会采用高精度的地面几何检校方法完成对立体视觉系统的检校测试。这些方法包括张正友的棋盘格检校法。这种方法在检校测试时,操作过程比较简单,占用测试空间较少。测试过程中,只需要使用绘制有棋盘格图案的检校板放置在相机视场的前方,通过变换检校板的多组位姿,同时相机对检校板成像的方式完成检校测试。但是,该方法也有缺点,检校结果不够稳定[1]。另外一种方法是直接线性变换法,这种方法通过直接建立三维空间中的点与二维图像上的点之间的线性变换关系估计出检校结果。这种方法具有不需要检校参数的初始值的优点,但是也具有检校结果精度不高的缺点[2]。第3种方法是多像空间后方交会法,这种方法在检校测试时,需要在相机视场前方布设三维检校场景,并需要借助经纬仪测量控制点的坐标。这种方法的优点是精度高、稳定性好;缺点是检校测试耗时长、需要预留较大的测试空间[3-4]。
发射后,火星车经过变轨、地-火转移、火星轨道停泊、软着陆过程后,立体视觉系统的几何参数会发生变化。因此,需要研究火星车立体视觉系统的几何自检校。相机自检校最早由文献[5]提出,该方法利用的是相机对同一场景拍摄至少两张具有一定重叠度的像片,建立核线变换关系求解Kruppa方程实现自检校,这是第1类自检校方法。该方法的缺点是精度不高,稳定性差,主要原因是核线变换对像素噪声非常敏感。之后,文献[6]提出了相机作纯旋转运动的自检校方法。第2类自检校方法,利用的是像片中的灭点。文献[7]提出了基于多像灭点的自检校方法。该方法主要是利用相机对建筑物进行多角度摄影,利用建筑物上存在的3个正交方向上的一簇空间平行线经过透视投影后,在像平面会汇聚在一点,即灭点。以灭点为桥梁,利用空间平行线与相机参数之间的关系实现自检校。该方法的优点是提高了自检校算法的精度和稳定性,缺点是检校场景中必须具有空间平行线以保证在像平面上能够提取到灭点。第3类自检校方法,针对立体相机的检校,文献[8]利用右相机到左相机存在的本征矩阵,提出了立体相机的自检校方法。文献[9]提出了立体相机的几何约束条件。对于这一类方法是利用立体像对中提取的同名点,恢复像对之间的单应性变换关系,进而求解出立体几何参数。本文采用导航相机A、B之间固定的几何关系,建立立体约束条件。第4类方法是基于联合平差[10]的自检校。文献[11]提出了一种基于多源多分辨率卫星影像的自检校方法。文献[12]提出了一种基于联合平差的资源3号卫星三线阵相机的自检校方法[12]。基于两组具有重叠度的影像建立相对几何约束及立体交汇约束。这一类方法具有精度高的优点,充分利用了多源数据提高平差系统的稳定性。本文也采用联合平差的方法,引入相对约束条件实现立体视觉系统的自检校。
桅杆机构用于承载云台,它具有很强的刚性和稳定性。因此,通过桅杆机构运动学建立一种自检校所需相对约束条件。常用的运动学建模方法是Denavit-Hartenberg(DH)参数法[13],这种方法是Denavit和Hartenberg于1955年提出的,该方法用4个变量α、a、θ、d来描述一个转动关节平移和旋转。这种方法的优点是机构建模时使用的变量少,建模过程简单;缺点是当相邻关节轴线运动到接近平行时,机构会出现奇异性问题。之后,很多学者在DH参数模型的基础上进行改进,得到了Hayati模型[14]、二阶模型[15]、S模型[16]和CPC模型[17],这些模型通过增加变量的方法来解决奇异性问题,但是又带了模型建立过程不直接、形式复杂、缺少通用性的问题。为了克服DH参数模型的缺点,文献[18]利用POE(product-of-exponentials)模型[19]对运动学参数进行检校。POE模型具有以下优点:实现了转动关节和平移关节的统一描述,具有通用性优点;当相邻关节轴线接近平行时,运动学模型像对关节运动是光滑变化的,不会出现奇异性问题[20]。
上述方法在解决相机自检校、立体参数估计及运动学参数辨识问题具有良好的效果,但是均无法直接应用于“祝融号”火星车立体视觉系统的自检校。因此,本文的目标是提出基于联合平差的“祝融号”火星车立体视觉系统高精度自检校方法,通过模拟试验验证自检校方法的精度。最后,采用该方法在火星表面完成“祝融号”立体视觉系统的自检校。
本文主要贡献为:①提出“祝融号”火星车立体视觉系统的高精度自检校方法;②使用该方法在火星表面完成“祝融号”火星车的几何自检校。
1 基于联合平差的自检校方法 1.1 坐标系定义建模过程涉及的坐标系定义如图 2所示。图像坐标系o-xy:原点o位于图像中心,x轴沿图像行指向右,y轴沿图像列指向上。导航相机i(i代表A或B)坐标系Oi-XiYiZi(i坐标系):原点Oi位于相机投影中心,Xi轴指向右、Yi轴指向上、Zi轴沿主光轴指向后。火星车本体坐标系OV-XVYVZV(V坐标系):原点OV位于火星车结构底板几何中心,XV轴指向右、YV轴指向前进方向、ZV轴沿铅垂线指向上。着陆点坐标系OS-XSYSZS(S坐标系):原点OS位于着陆点,XS轴指向北、YS轴指向东、ZS轴沿铅垂线指向地。

|
| 图 2 坐标系定义 Fig. 2 Definition of coordinate systems |
1.2 自检校流程
“祝融号”火星车发射前,在火星车结构顶板上均匀布设30个控制点。然后,采用经纬仪测量出控制点在V坐标系下的三维坐标。发射前,设计好导航相机A、B的成像策略:导航相机A、B回望下俯对控制点进行序列立体成像,连续拍摄多对具有重叠度的立体像对,从立体像对中可以观察到控制点。导航相机A、B拍照的同时,记录下来桅杆机构3个转动关节的转角值。
“祝融号”火星车着陆火星之后,按照既定的拍照策略获取序列立体像对。自检校数据处理时,先对导航相机A和导航相机B拍摄的一对独立立体像对进行特征匹配。影像匹配是摄影测量的一个经典研究方向[21],本文采用SIFT算子。然后,采用RANSAC算子剔除误匹配点。最后,对两两立体像对之间采用相同的方法进行特征匹配。匹配结束后,由于每对立体像对对应的桅杆3个关节转角是已知的,可以采用桅杆机构正向运动学模型(式(4))计算出立体像对的外方位元素。有了立体像对的外方位元素,可以完成相对定向工作。此时,引入控制点对立体模型条带进行平差,估计出加密点在V坐标系下的三维坐标。采用自检校光束法平差模型,输入加密点坐标、导航相机A、B的内方位元素和外方位元素;同时,引入立体约束和桅杆机构运动约束,建立联合平差模型完成自检校。
1.3 自检校光束法平差自检校光束法平差的基本模型源于共线方程式
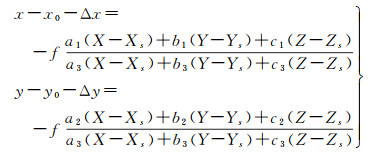 (1)
(1)
式中,(x, y)表示像点坐标;(x0, y0)表示像主点坐标;(Δx, Δy)表示畸变差;f表示主距;(X, Y, Z)表示物方点在火星车本体系下的坐标;(Xs, Ys, Zs)表示相机坐标系到火星车本体坐标系的平移参数;a1, a2, …, c3表示由外方位角元素(φ, ω, κ)构成的旋转矩阵R的方向余弦。相机镜头的畸变采用以下模型描述
 (2)
(2)
式中,k1、k2表示镜头的径向畸变参数;p1、p2表示镜头的切向畸变参数;r表示像点坐标的向径。
1.4 立体约束对于导航相机A、B,由于导航相机A和导航相机B构成了立体相机,B相机为左相机,A相机为右相机,它们之间的几何关系是固定的。因此,可以建立立体约束条件[9]
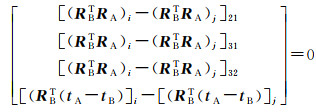 (3)
(3)
式中,RB是导航B像片的旋转矩阵;RA是导航A像片的旋转矩阵;TB是导航B像片的位移矢量;TA是导航A像片的位移矢量。下标i和j表示第i对立体像对和第j对立体像对。下标数字表示计算后所得矩阵的行、列号,例如:21表示所得矩阵的第2行、第1列。式(3)中包含了两对立体像对相关4张像片的外方位元素。
立体约束条件的物理意义如图 3所示。

|
| 图 3 立体约束条件的物理意义 Fig. 3 Physical meanings of stereo constraints |
1.5 桅杆机构约束
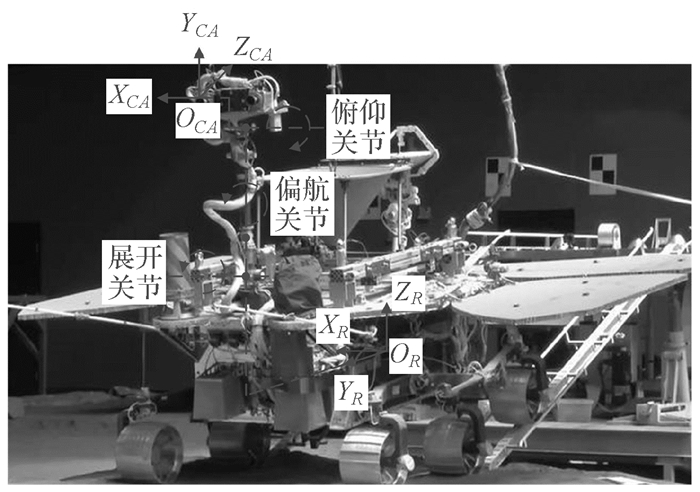
采用POE公式建立了桅杆机构的正向运动模型[20-22]。当桅杆机构位于零位时,坐标系及各关节转动极性的定义,如图 4所示。在图 4中,用半圆形标注了关节轴的转动极性,箭头方向代表关节轴的正转方向。
|
| 图 4 桅杆机构位于零位状态 Fig. 4 Mast mechanism in the zero position |
基于POE公式建立的桅杆机构的正向运动模型,见式(4)
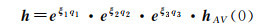 (4)
(4)
式中,h表示4×4的齐次矩阵,它表示A坐标系到V坐标系的旋转和平移;eξiqi是一个4×4的矩阵,它表示第i个转动关节的指数积表达式;ξi是第i个关节的旋量;qi是第i个关节的转动角;hAV(0)表示当桅杆机构位于零位状态时,A坐标系到V坐标系的位姿矩阵。式(4)是非线性的,采用一阶泰勒级数进行线性化,只考虑关节旋量作为未知数。在等式左右两边同时乘以h-1,得到桅杆机构的误差方程,见式(5)
 (5)
(5)
在式(5)左边,令ha表示由激光跟踪仪测量得到的A坐标系到V坐标系的实际位姿矩阵。令hn表示由理论运动学参数代入式(4)后算得的理论位姿矩阵。δhh-1表示在V坐标系下描述的ha与hn之间的偏差,它可以采用式(6)进行计算。ζ=[ξ]V,定义为旋量ξ的旋量坐标
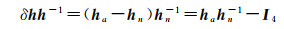 (6)
(6)
假设对导航相机A进行了m次测量,则可以得到线性化表达式(7)
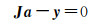 (7)
(7)
式中,a=(δζ1, δζ2, δζ3)T表示3个转动关节(包括展开关节、偏航关节、俯仰关节)旋量的增量;y=[δhh-1]V表示导航相机A位姿的残差矢量;J表示对应的偏导数项构成的系数矩阵。
1.6 联合平差模型在1.4节和1.5节推导了立体约束条件和桅杆机构运动约束条件,可以将它们作为相对约束条件,加入自检校光束法平差模型中进行联合估计,得到如式(8)所示的附有约束条件的误差方程
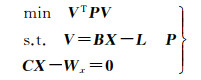 (8)
(8)
式(8)描述的是一个附有约束条件的间接平差问题,可以采用加权最小二乘法进行最优估计求解。X=[x, t, a]T代表待求解的几何参数。x表示导航相机B和导航相机A的内方位元素、畸变系数、外方位元素的增量;t表示导航相机B和导航相机A的外方位元素增量;a表示桅杆机构的3个转动关节,分别为:展开关节、偏航关节、俯仰关节的旋量的增量。P代表权矩阵,采用验后权估计法进行定权[23],本文采用Förstner验后方差估计公式[24]。本文采用自动提点方法提取控制点在图像上对应的像点坐标,因此,可以保证像片坐标为等精度观测值。测量控制点时,经纬仪布设完毕后不再搬站,测量过程中不更换测量员,建立坐标系和测量控制点在2 h内完成,且采用人工靶标,因此,可以保证控制点为等精度观测值。依据以上的试验保障,将控制点处理为固定点求解。B和C表示对应的系数矩阵。L表示像点坐标的残差矢量。Wx表示分别由:导航相机A、B的外方位元素构成的残差矢量与桅杆机构末端位姿构成的残差矢量。V=[v, 0, 0]T表示像点坐标观测值的改正量。B和C,L和Wx的表达式,见式(9)
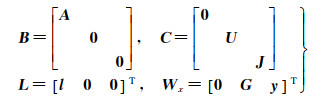 (9)
(9)
式中,A代表像点观测值x、y对未知数(导航相机B和导航相机A的内方位元素、畸变系数、外方位元素)求偏导数后构建的系数矩阵;U代表式(3)对未知数(导航相机B和导航相机A的外方位元素)求偏导数后构建的系数矩阵;G代表将平差计算后得到的未知数代入式(3)得到的常数值。式(8)的解,见式(10)
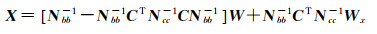 (10)
(10)
式中,一些未定义的矩阵和矢量参见式(11)
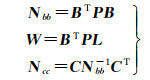 (11)
(11)
单位权中误差的计算方法,见式(12)
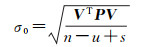 (12)
(12)
式中,σ0表示单位权中误差;n表示观测值个数;u表示未知数个数;s表示约束条件个数。未知数的中误差计算方法,见式(13)
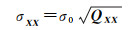 (13)
(13)
式中,σXX表示未知数的中误差。QXX表示协因数矩阵,它的计算方法见式(14)
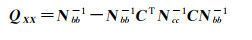 (14)
(14)
“祝融号”火星车遥操作任务的自检校试验及精度检核试验在文昌航天发射场及河北丰宁县进行。文昌航天发射场预留100 m2试验区域;洁净度为105级,光照均匀且充足。此外,试验区还配备了高精度测量设备,包括室内GPS、激光跟踪仪、工业经纬仪、三维激光扫描仪等。在河北丰宁县的野外环境下开展了自检校试验。野外地形以裸露的碎石、沙土和河道为主,这里气候干燥并伴有大风,地形与气候条件与火星环境具有较高的相似性。为了充分验证“祝融号”火星车的状态并演练遥操作任务,研制了“祝融号”火星车验证器,验证器除了不具备飞行功能外,其他设计均与“祝融号”火星车相同。试验时,火星车位于整备支架车上,车体距离地面约0.5 m高度。
2.2 试验结果在导航相机A、B自检校试验中,在火星车体上布设了30个控制点,如图 5所示。

|
| 图 5 在火星车上布设的控制点 Fig. 5 In-orbit GCPs on the rover |
图 5中的控制点数量不足30个,该图像是导航相机B拍摄于火星车外场试验的自检校场景图像,拍摄时间是2018年5月。在图 5中,红色的数值代表控制点的编号,红色十字丝代表控制点位。对控制点在V坐标系下的三维坐标进行测量。测量仪器是徕卡TM5100A,测角精度0.5″,最短视距0.6 m,物镜孔径52 mm,放大倍率为32。测量时,经纬仪1摆放在火星车正前方1.2 m处,距离地面高度0.5 m;经纬仪2摆放在火星车右侧1.5 m处,距离地面高度2.8 m;经纬仪3摆放在火星车左侧1.5 m处,距离地面高度2.8 m。测量时采用3台经纬仪,利用1号经纬仪准直-YV轴,利用2号经纬仪准直-XV轴,然后拟合出+ZV轴,从而建立V坐标系。最后,利用3号经纬仪与1、2号经纬仪组合,采用双测回前方交会法,测量出控制点在V坐标系下的三维坐标。控制点的测量精度优于0.2 mm。在桅杆机构运动试验中,以较小的偏航和俯仰变化角度设计了桅杆机构以不同构型的24次运动。将估计出的导航相机B的外方位元素作为桅杆机构末端的位姿。在提取控制点的图像坐标时,采用自动提点方法。对于圆形靶标的圆心,采用椭圆拟合法提取[25]。然后,对于直线格网的交点,采用最小二乘直线拟合法[26-27]。最后,对圆心坐标和直线交点坐标求取平均值。
自检校试验过程中,导航相机A、B回望并下俯拍摄车体顶部的控制点,共获取的24对立体像对。采用本文提出的自检校方法估计出导航相机A、B的内方位元素、外方位元素和桅杆机构的旋量参数。这些参数的中误差参见表 1。
| 检校参数 | 导航相机B | 导航相机A |
| σx0/px | 1.046 | 0.832 |
| σy0/px | 2.891 | 2.59 |
| σf/px | 2.814 | 2.608 |
| σk1 | 5.721×10-10 | 4.477×10-10 |
| σk2 | 2.435×10-16 | 3.437×10-16 |
| σp1 | 6.349×10-8 | 6.284×10-8 |
| σp2 | 7.924×10-8 | 3.354×10-7 |
| σX/mm | 0.4 | 0.3 |
| σY/mm | 0.8 | 0.7 |
| σZ/mm | 1.5 | 0.9 |
| σφ/rad | 0.000 81 | 0.000 62 |
| σω/rad | 0.001 14 | 0.000 89 |
| σκ/rad | 0.000 71 | 0.000 57 |
为了验证自检校结果的几何精度,设计了以下两组自检校精度检核试验。
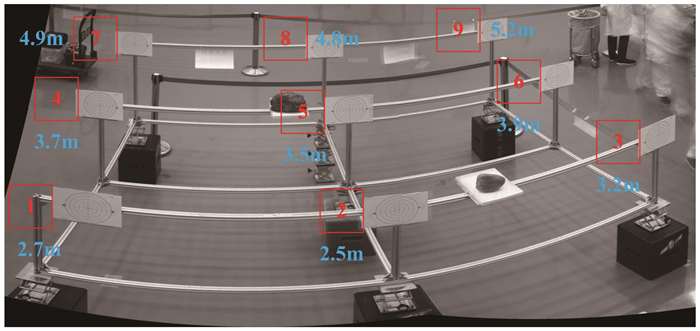
验证1:在文昌航天发射场开展了导航相机A、B引导的激光诱导击穿光谱(laser induced breakdown spectroscopy, LIBS)联合试验。LIBS是将高能量的激光脉冲聚焦于探测目标上,通过对样品烧蚀,瞬间气化,产生高能量、高温度、高密度的等离子体;同时采集等离子体演化过程中所辐射的光谱,依据辐射元素的特征谱线位置和强度等信息进行定性和定量分析,进而确定物质元素的组成及含量[28]。联合试验时,布设了一种检核场景(图 6),该场景由9个检核点组成,用于验证自检校参数的精度。图 6中,红色线框及数值代表检核点号;蓝色数值标明的是该点到火星车的距离,单位为m。使用本文方法估计出的导航相机A、B几何参数估计出检核点在V坐标系下的三维坐标。利用经纬仪测量出检核点在V坐标系下的三维坐标。将检核点的视觉估计坐标与测量坐标进行对比,结果见表 2。
|
| 图 6 检核试验1 Fig. 6 Verify experiment 1 |
| 方法 | 平均值 | 最小值 | 最大值 |
| 本文方法 | 3.89 | 0.32 | 8.72 |
| 检校方法1 | 8.1 | 3.59 | 13.57 |
| 检校方法2 | 5.37 | 2.57 | 10.4 |
| 检校方法3 | 6.83 | 2.95 | 11.82 |
| 灭点法 | 15.73 | 7.81 | 20.42 |
| Kruppa法 | 16.52 | 7.36 | 22.69 |
在该检核试验中,本文方法是指在自检校光束法平差的基础上引入了立体约束条件和桅杆机构约束条件。检校方法1代表未引入这两种约束条件所估计出的精度。检校方法2代表仅引入立体约束条件所估计出的精度。检校方法3代表仅引入桅杆机构约束条件所估计出的精度。灭点法是指文献[7]提出的基于多像灭点的自检校方法估计出的精度。Kruppa法是指文献[5]提出的计算机视觉自检校方法估计出的精度。对于本文方法,误差最小值对应的是3号点,误差最大值对应的是8号点。
验证2:2021年5月22日,“祝融号”火星车成功登陆火星表面。着陆后,火星车在驶离着陆平台之前,在顶部环拍点对着陆点周围的地形进行了环视成像,拍摄了360°环视立体像对,共获取了14对立体像对,自检校使用的原始图像如图 7所示。采用本文提出的自检校方法估计出立体视觉系统的几何参数。在同一立体像对中,左右像片的特征匹配结果参见图 8。然后,将自检校参数代入立体前方交会算法,估计出检核点在V坐标系下的三维坐标。火星车发射前,在火星车体顶板上布设的光学太阳能反射片(OSR)上选取了30个角点作为在轨控制点使用,采用经纬仪测量了这些控制点在V坐标系下的三维坐标。基于以下3点确保控制点不发生较大的相对偏移:①OSR片采用高强度、耐高低温、抗变形的轻型材料,火星车发射前,在空间环境模拟器中进行热试验,测量出控制点的变形阈值,确保控制点的相对偏移可控;②火星车结构顶板是一个稳定的刚体,控制点布设在其上可以保证相对偏移最小;③布设了远超所需数量的控制点,对于残差大的控制点可以从平差中予以剔除。由图 7可以看出,在轨拍摄的图像中只可以观察到其中的25个控制点。在这25个控制点中,保留其中的7个点作为检核点(点号为:4、25、9、12、18、19、16),其余的作为控制点。检核点不参与自检校。将检核点的在轨视觉估计坐标与发射前的测量坐标进行对比。对比时,先求取XYZ 3个方向上的差值(dX, dY, dZ),然后再按照公式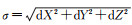

|
| 图 7 自检校使用的原始图像及控制点分布 Fig. 7 Original images for self-calibration and GCPs layout |

|
| 图 8 立体像对(L6-R6)的特征匹配结果 Fig. 8 Match of stereo pair (L6-R6) |
| 点号 | 距离 | 中误差 |
| 4 | 0.7 | 6.2 |
| 25 | 1.0 | 8.3 |
| 9 | 1.7 | 9.4 |
| 12 | 2.0 | 14.1 |
| 18 | 2.1 | 15.6 |
| 19 | 2.2 | 15.1 |
| 16 | 2.5 | 17.5 |
图 7中,红色的数值代表检核点号,红色的十字丝代表该点在火星车上的位置。
在图 8中,蓝色的连接线表示有效的匹配点;红色的连接线表示无效的匹配点。该立体像对是导航相机A、B在顶部环拍点拍摄的第6对立体像对。仅依靠控制点及其在图像上对应的像点无法保证自检校具备足够数量且空间分布均匀的像控点,特征匹配点坐标可以为联合平差(式(8))提供更多的观测值。此外,在立体模型条带平差中,引入控制点可以对加密模型点坐标进行修正,进而为联合平差提供更多数量、高精度且空间分布均匀的像控点。
表 3中的距离是指检核点到导航相机B的距离。
3 讨论由表 1的检校参数的中误差结果来看,内方位元素和外方位元素的中误差比较小,这说明本文方法具有较高的理论精度。从外方位线元素的中误差可以看出,沿Z方向的误差要大于XY方向的误差,这是由于在轨控制点布设在火星车结构顶板上,它们沿Z轴的坐标分量差别不大,这就造成在Z方向上的控制强度要弱于XY方向。此外,导航相机A的内外方位元素中误差与导航相机B的内外方位元素中误差差别不大,这说明本文方法具有较高的稳定性。
由表 2的统计结果可以看出,本文方法与其他5种方法相比较,具有最高的检核点精度。将本文方法与检校方法1相比较,说明引入立体约束及桅杆机构约束能够有效提高精度。将检校方法1与检校方法2相比较,说明引入立体约束条件能够有效提高精度。将检校方法1与检校方法3相比较,说明引入桅杆机构约束条件能够有效提高精度。将检校方法2与检校方法3相比较,说明引入立体约束条件对精度的提升要比引入桅杆机构约束条件显著。将本文方法与检校方法2、检校方法3相比较,说明同时引入两种约束条件对精度的提升要比仅引入某一种约束条件显著。随着检核点到火星车的距离增大,误差也会增大。“祝融号”火星车具有强大的越野能力,设计最大越障高度为200 mm,对于直径小于150 mm的石块、坑等障碍物,地面“祝融号”遥操作任务支持中心不需要制定额外的行驶策略,火星车可以直接行驶通过。因此,对于自检校几何参数的使用,建议在导航相机的最佳成像距离内(5~7 m)开展遥操作任务。
由图 7可以看出,特征匹配算法可以匹配出数量可观的有效同名点。特征匹配结果可以为联合平差模型提供更多数量且空间分布均匀的观测值。通过模型连接,可以计算出加密点的三维坐标。在立体模型的条带平差时引入控制点,可以对加密点坐标进行修正。特征匹配点及其对应的加密点为联合平差提供了更多数量、高精度且空间分布均匀的像控点。
由表 3可知,经过火星真实数据的验证,证明本文方法具有较高的自检校精度,在3 m以内的可视范围内,可以达到优于2 cm的检核点精度。本文方法可以有效地支持“祝融号”火星车在火星表面完成自检校任务。
对比表 3和表 2的统计结果,可以发现地面模拟验证精度与火星表面真试验证精度保持了较高的一致性。这证明本文方法的稳定性及立体视觉系统的可靠性。
4 结论2021年5月22日,我国首辆火星车“祝融号”成功登陆火星表面。截至2021年8月22日,“祝融号”火星车在火星表面安全行驶了90 d。这标志着我国首次火星探测任务圆满完成,也为未来我国计划实施的火星采样返回、月球南北极探测及小行星探测任务奠定了基础。本文提出了一种火星车立体视觉系统自检校方法,在联合平差模型中,加入了导航相机A、B的立体约束条件和桅杆机构的运动约束条件。
在地面模拟检核精度验证试验中,获得的检核点中误差的平均值为3.89 mm,最小值为0.32 mm(距离火星车3.2 m),最大值为8.72 mm(距离火星车4.8 m)。在火星表面真实试验中,获得的检核点中误差的平均值为12.3 mm,最小值为6.2 mm(距离导航B相机0.7 m),最大值为17.5 mm(距离导航B相机2.5 m)。经过地面模拟试验和火星真实任务验证,证明本文方法能够对“祝融号”火星车的立体视觉系统实施高精度的自检校,有效地保障了“祝融号”火星车遥操作任务的圆满完成。
| [1] |
ZHANG Z. A flexible new technique for camera calibration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1330-1334. DOI:10.1109/34.888718 |
| [2] |
冯文灏, 李建松, 闫利. 基于二维直接线性变换的数字相机畸变模型的建立[J]. 武汉大学学报(信息科学版), 2004, 29(3): 254-258. FENG Wenhao, LI Jiansong, YAN Li. Creation of distortion model for digital camera based on 2D DLT[J]. Geomatics and Information Science of Wuhan University, 2004, 29(3): 254-258. |
| [3] |
张烁, 徐亚明, 刘少创, 等. 嫦娥-3号月面巡视探测器立体相机的控制场检校[J]. 武汉大学学报(信息科学版), 2015, 40(11): 1509-1513. ZHANG Shuo, XU Yaming, LIU Shaochuang, et al. Calibration of Chang'e-3 lunar rover stereo-camera system based on control field[J]. Geomatics and Information Science of Wuhan University, 2015, 40(11): 1509-1513. |
| [4] |
ZHANG S, PENG S, WU Y, et al. Positioning accuracy of the Zhurong Mars Rover's Hand-Eye system[J]. The Photogrammetric Record, 2022, 37(177): 61-86. DOI:10.1111/phor.12401 |
| [5] |
FAUGERAS O D, LUONG Q T, MAYBANK S J. Camera self-calibration: theory and experiments[C]//Proceedings of 1992 European conference on computer vision. Berlin: Springer, 1992: 321-334.
|
| [6] |
HARTLEY R I. Self-calibration from multiple views with a rotating camera[C]//Proceedings of 1994 European Conference on Computer Vision. Berlin: Springer, 1994: 471-478.
|
| [7] |
谢文寒, 张祖勋. 基于多像灭点的相机定标[J]. 测绘学报, 2004, 33(4): 335-340. XIE Wenhan, ZHANG Zuxun. Camera calibration based on vanishing points of multi-image[J]. Acta Geodaetica et Cartographic Sinica, 2004, 33(4): 335-340. DOI:10.3321/j.issn:1001-1595.2004.04.011 |
| [8] |
谭晓军, 余志, 李军. 一种改进的立体摄像机标定方法[J]. 测绘学报, 2006, 35(2): 138-142. TAN Xiaojun, YU Zhi, LI Jun. An improved method of stereo camera calibration[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(2): 138-142. DOI:10.3321/j.issn:1001-1595.2006.02.009 |
| [9] |
郑顺义, 黄荣永, 郭宝云, 等. 附约束条件的立体相机标定方法[J]. 测绘学报, 2012, 41(6): 877-885. ZHENG Shunyi, HUANG Rongyong, GUO Baoyun, et al. Stereo-camera calibration with restrictive constraints[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(6): 877-885. |
| [10] |
SONG Yingchun, XIA Yuguo, XIE Xuemei. Adjustment model and algorithm based on ellipsoid uncertainty[J]. Journal of Geodesy and Geoinformation Science, 2020, 3(3): 59-66. |
| [11] |
TANG Shengjun. Combined adjustment of multi-resolution satellite imagery for improved geo-positioning accuracy[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2016, 114: 125-136. DOI:10.1016/j.isprsjprs.2016.02.003 |
| [12] |
YANG B, PI Y, LI X, ET AL. Integrated geometric self-calibration of stereo cameras onboard the ZiYuan-3 satellite[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2020, 162: 173-183. DOI:10.1016/j.isprsjprs.2020.02.015 |
| [13] |
DENAVIT J, HARTENBERG R. A kinematic notation for lower-pair mechanisms based on matrices[J]. ASME Journal of Applied Mechanics, 1955, 77: 215-221. |
| [14] |
HAYATI S, TSO K, ROSTON G. Robot geometry calibration[C]//Proceedings of 1988 IEEE International Conference on Robotics and Automation. Philadelphia: IEEE, 2002: 947-951.
|
| [15] |
VEITSCHEGGER W, WU C H. Robot accuracy analysis based on kinematics[J]. IEEE Journal on Robotics and Automation, 1986, 2(3): 171-179. DOI:10.1109/JRA.1986.1087054 |
| [16] |
STONE H, SANDERSON A. A prototype arm signature identification system[C]//Proceedings of 1987 IEEE International Conference on Robotics and Automation. 1987, Raleigh: IEEE, 2003: 175-182.
|
| [17] |
ZHUANG H, ROTH Z S, HAMANO F. A complete and parametrically continuous kinematic model for robot manipulators[C]//Proceedings of 1992 IEEE International Conference on Robotics and Automation. [S. l. ]: IEEE, 1992: 92-97.
|
| [18] |
MURRAY R M, LI Zexiang, SASTRY S S. A mathematical introduction to robotic manipulation[M]. Florida: CRC Press, 2017.
|
| [19] |
OKAMURA K, PARK F. Kinematic calibration using the product of exponentials formula[J]. Robotica, 1996, 14(4): 415-421. DOI:10.1017/S0263574700019810 |
| [20] |
CHEN Genliang, WANG Hao, LIN Zhongqin. Determination of the identifiable parameters in robot calibration based on the POE formula[J]. IEEE Transactions on Robotics, 2014, 30(5): 1066-1077. DOI:10.1109/TRO.2014.2319560 |
| [21] |
GUO Wenyue, YU Anzhu, SUN Qun, et al. A multisource contour matching method considering the similarity of geometric features[J]. Journal of Geodesy and Geoinformation Science, 2020, 3(3): 76-87. |
| [22] |
HE Ruibo, ZHAO Yingjun, YANG Shunian, et al. Kinematic-parameter identification for serial-robot calibration based on POE formula[J]. IEEE Transactions on Robotics, 2010, 26(3): 411-423. DOI:10.1109/TRO.2010.2047529 |
| [23] |
李德仁. 地面坐标作为带权观测值的空间后方交会与验后权估计[J]. 武汉测绘学院学报, 1981, 6(1): 52-62. LI Deren. On the space resection with ground coordinates as weighted observations and a posteriori weight estimation[J]. Geomatics and Information Science of Wuhan University, 1981, 6(1): 52-62. |
| [24] |
李德仁. 验后方差估计的几种方法[J]. 武测资料, 1981, 6(S1): 1-11. LI Deren. Several methods of posterior variance estimation[J]. Journal of Geomatics, 1981, 6(S1): 1-11. |
| [25] |
FITZGIBBON A, PILU M, FISHER R B. Direct least square fitting of ellipses[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1999, 21(5): 476-480. DOI:10.1109/34.765658 |
| [26] |
HU Xiangyun, ZHANG Zuxun, TAO C. A robust method for semi-automatic extraction of road centerlines using a piecewise parabolic model and least square template matching[J]. Photogrammetric Engineering & Remote Sensing, 2004, 70(12): 1393-1398. |
| [27] |
DI Kaichang, WAN Wenhui, ZHAO Hongying, et al. Progress and applications of visual SLAM[J]. Journal of Geodesy and Geoinformation Science, 2019, 2(2): 38-49. |
| [28] |
舒嵘, 徐卫明, 刘向锋, 等. 火星表面成分探测仪中激光诱导击穿光谱的地面综合标定与验证[J]. 中国科学: 物理学力学天文学, 2022, 52(3): 55-70. SHU Rong, XU Weiming, LIU Xiangfeng, et al. Ground calibration and validation of laser-induced breakdown spectroscopy for the Mars surface composition detector[J]. Scientia Sinica (Physica, Mechanica & Astronomica), 2022, 52(3): 55-70. |



