2. 湖南大学机器人学院,湖南 长沙 410012
2. School of Robotics, Hunan University, Changsha 410012, China
高光谱成像在电磁波谱的紫外、可见光、近红外、中波甚至长波红外区域,利用光谱仪获取上百个不同谱段的图像数据,是一种图谱合一的探测技术。通常,一幅高光谱图像(hyperspectral image, HSI)相当于数百幅灰度图像,不仅记录了场景中物体丰富的空间结构,同时图像中每一个像元都对应一条与场景中物体材质相关的光谱曲线,精细地刻画了物体纳米级的精细光谱特征[1-2]。
一直以来,世界各国争相发展高光谱探测技术,研制了一系列的航空与航天高光谱成像系统,例如美国的AVIRIS-NG、法国和挪威的SYSIPHE、加拿大的CASI-1500及我国的FAHI、APHIS等机载高光谱成像装置。此外也出现了印度的HySIS、意大利的PRISMA HSI、美国的OCI及我国的VNIS、AHSI等更加先进的星载高光谱成像装置[3-4]。学者们利用机载与星载高光谱遥感数据分析地物光谱特性,为地物的精确探测与识别带来了前所未有的机遇,在精准农业、环境监测、资源调查、军事侦察等领域发挥了十分重要的作用[5-12]。
然而,作为一种光学遥感技术,高光谱遥感图像不可避免地受到成像机理、大气条件、环境光照等因素的影响,导致高光谱图像的光谱信息、环境光照及其他信息相互耦合。即一个像元的光谱不仅由其反射率所决定,而且会受到其周围像素的反射率、环境光照的强度和光谱特性、成像仪及各种因素导致的图像噪声等的影响,最终出现“同物异谱”“异物同谱”的现象[13]。近年来,高光谱图像本征信息分解技术得到了越来越多的关注[14]。其核心思想是抑制复杂环境因素对物体光谱与空间特征的影响,准确提取并表征物体最本征的光谱与空间信息,提升高光谱图像的识别与解译性能。
高光谱图像本征信息分解是高光谱遥感图像处理与应用中一项重要的研究内容。相对于图像去噪的目的是去除图像中的噪声,复原场景真实的图像信息;高光谱图像本征信息分解的最终目标是要将图像分解成纯净的光谱反射率成分、光照成分、噪声成分、大气成分等最本征的信息。这些成分信息往往具备很明确的物理含义。因此,研究高光谱图像本征信息分解技术,可助力研究人员从根本上解决高光谱图像“同物易谱”“异物同谱”难题,为提升高光谱图像识别与定量化反演能力奠定基础。
本文总结了高光谱图像本征信息分解技术的核心本征信息耦合模型与本征信息求解方法,阐述了高光谱图像本征信息分解面临的挑战、尚待解决的问题及可能的解决途径,并对高光谱图像本征信息分解的应用前景进行了展望。
1 高光谱图像本征信息分解方法早在公元10世纪,光学领域著名学者阿尔哈曾(Alhazen)就曾指出:“人眼能够感知到的只是光的强度和颜色,其他信息都是通过洞察、推理、识别等方法来获取的”。换言之,光的强度和颜色是人眼所能感知到的最重要的两种本征信息。其中,光的强度对应成像场景中各个位置的光的强度,与成像场景中物体的几何形状、光源的强度和方向等因素相关。颜色则与物体在可见光区间对不同波长电磁波谱的反射率相关,反映了物体的反射特征。1978年,基于阿尔哈曾的论述,“本征分解”的概念被首次提出,并发展成为计算机视觉领域的一个重要研究方向[15]。
在高光谱遥感领域,“同物易谱”“异物同谱”一直是制约高光谱图像识别与理解性能的一大核心难题。究其根本原因是由于光谱成像过程受到拍摄环境、气候条件等因素的影响,图像中记录的光谱反射值往往并不纯净,甚至可能包含严重的失真与畸变。针对这一难题,文献[16]首次提出了一种基于本征信息分解的高光谱图像特征提取方法。其核心思想是通过对高光谱图像进行本征分解,将场景最本征的空间与光谱特征从原始图像中分离出来,为地物纯净光谱反射特征与复杂空间结构的准确表征提供了思路。近两年来,不断有学者围绕高光谱图像本征信息分解开展研究[14, 17-18]。为了更准确地估计高光谱图像的纯净光谱反射成分,文献[19]构建了针对多光谱图像本征分解的公用数据集,提供可参考的多光谱反射率图与光照图,为验证不同类型本征分解方法的性能提供了支撑。文献[20—21]提出了基于超像素的高光谱图像本征光谱特征提取方法和结合反射与光照先验的高光谱图像本征分解模型,发现在高光谱图像本征分解模型中引入适用于高光谱图像的先验约束,能够获得更优的本征分解性能。此外,高光谱图像本征分解模型能够有效去除光照不均、噪声等因素导致的地物光谱变化,获取的本征光谱反射率图与原始高光谱图像相比,辨识度更高,地物的识别精度得到了显著提升。高光谱图像本征信息分解已逐渐发展成为高光谱遥感领域的一个独特分支[14, 16-21]。
1.1 本征信息耦合模型本征信息耦合模型旨在对成像过程中光的强度和颜色的相互耦合过程进行建模。
在计算机视觉领域,对于红-绿-蓝(red-green-blue, RGB)图像而言,其本征图像分解问题可以被描述为[16]
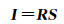 (1)
(1)
式中,I代表原始图像;R为反射率成分;S为光照成分。由于彩色图像的3个通道集中在很窄的光谱区间内,一般假设场景光照变化对这3个通道产生同比例的影响,即彩色图像的光照成分与波长无关。
与上述对RGB图像的基本假设不同,HSI由被动成像传感器采集,接收到的能量主要是太阳辐射反射的能量,其涵盖的波段包含可见、近红外、中红外甚至远红外波段。由于不同光谱区间内的波段对场景亮度变化的灵敏度不全相同,这意味着不同波段的像素值将随场景亮度变化发生非等比例变化,此时RGB图像的本征分解模型不再适用于高光谱图像。考虑到HSI中光照成分对每个波长产生的影响不同,因此得到高光谱图像的本征分解模型如下[21]
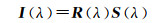 (2)
(2)
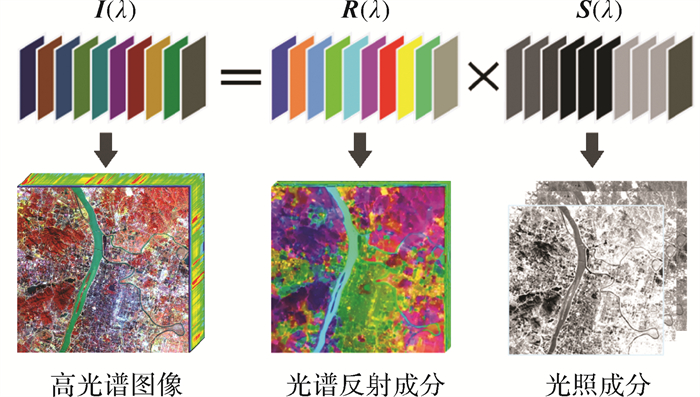
式中,λ为波长;R(λ)与S(λ)分别代表波长λ处的反射成分与光照成分。图 1为HSI的本征分解模型。
|
| 图 1 HSI的本征分解模型 Fig. 1 Intrinsic decomposition model for HSIs |
从图像超分辨率的角度出发,更高空间分辨率的图像可以为高光谱图像提供额外的信息,如激光雷达图像(light detection and ranging, LiDAR),从而可以获取亚像素的反射率和光照成分,其本征分解模型可以简化为
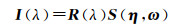 (3)
(3)
式中,η为亚像素的表面法线向量;ω为场景中均匀分布的照射光线;R(λ)为各亚像素在波长λ处的反射成分;S(η, ω)代表各亚像素的光照成分。具体的计算公式取决于如何实现具有不同数据结构和分辨率的LiDAR点云子集和HSI像素之间的映射。
此外,为方便计算,常在对数域中开展图像本征信息分解的研究,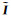
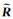
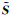
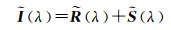 (4)
(4)
考虑到光照成分可以被进一步分解为照明和几何成分,文献[22—24]提出了一种细化的本征分解模型,可以直接恢复图像的反射、几何和照明成分
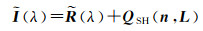 (5)
(5)
式中,n表示像素表面不同方向的法线分布;L表示球谐光照(spherical-harmonic, SH)参数。在计算机图形学中,球面谐波可以作为光照信息的载体,QSH(n, L)即为建立的球谐光照模型,它可以被用来重建辐射光照成分。
高光谱成像环境复杂,上述模型仅适用于传统高光谱图像。在遇到特殊情况时,例如高光谱图像中存在较强噪声、云雾、光照及阴影等,高光谱图像本征信息分解模型需要将这些变化因素考虑在内,在这里首次提出面向复杂场景的本征分解理论模型
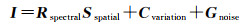 (6)
(6)
式中,Rspectral为高光谱图像的光谱反射成分;Sspatial为高光谱图像的空间光照成分;Cvariation为特殊环境下的变化成分,即较强噪声、云雾、光照及阴影等;Gnoise为高光谱成像过程中存在的固有噪声。
1.2 本征信息分解方法输入一幅图像,本征信息分解旨在将该图像分解为反射率图和光照图,光照图表示图像中各个位置的光照信息,而反射率图表示物体各个位置的反射率信息。如式(1)和式(2)所示,在分解过程中,由于只有一个已知量,但有两个需要求解的未知量,因此仅从数学方程式求解的角度,本征信息分解是一个无穷多解的欠定问题。针对这一难题,学者们提出了一系列本征信息分解方法。这类方法,按照输入图像不同,可以分为彩色图像本征信息分解与高光谱图像本征信息分解方法。
1.2.1 彩色图像本征信息分解方法彩色图像本征信息分解是计算机视觉和图形图像领域的一个挑战性难题。由于目前计算机视觉和图像处理中的很多任务,例如图像分割、三维重建、增强现实等,都会受到颜色纹理或光照的干扰,本征信息分解在计算机视觉领域具有十分重要的研究意义。研究人员在彩色图像本征信息分解问题上进行了大量的研究,根据采用的方法不同,可以分为基于优化模型的本征信息分解方法与基于学习模型的本征信息分解方法。
1.2.1.1 基于优化模型的方法在早期的研究中,学者们通常是通过对本征信息分解问题进行抽象建模,刻画出反射图、光照图与输入图像之间的物理关系,然后通过各类优化方法来对模型进行求解。然而,本征信息分解这一问题是一个无穷多解的欠定问题,为解决这一难题,研究人员通过对自然图像的观察和分析,在求解过程中引入了一系列设计好的先验约束,使得本征信息分解从无穷多解到有唯一解。
最经典的先验约束之一是Retinex约束。Retinex是retina(视网膜)和cortex(皮层)两个单词组成的一个合成词。该约束重点考虑了人类视觉系统的感知机理,假设光照均匀的情况下,输入图像的梯度图中,较显著的梯度变化通常是由反射率变化引起的,而较平缓的梯度变化则是由光照变化引起的。基于这个假设,通过最小化反射图和光照图的梯度图,对本征分解问题进行求解。文献[25]提出沿着图像中两个不同点之间的路径对强光照梯度进行重积分,来计算相应的反射率。文献[26]提出了基于Retinex约束的彩色图像本征信息分解方法,并搭建了定制的实验室环境,构建了包含真实彩色图像和它们的真实反射和光照图的MIT数据集,为后续彩色图像本征信息分解方法性能的验证和评测奠定了数据基础。然而,Retinex约束给出的假设只有在理想情况下才能达到。真实自然场景下,光照分布不一定均匀,光照强度变化也不一定缓慢,导致这类方法在真实自然图像上的性能并不能令人满意。
全局约束/非局部约束作为另一种代表性的图像先验特性,在彩色图像本征信息分解中也得到了广泛的应用。文献[27]认为局部图像区域比单个像素更能概括图像强度和相对位置的变化,由此设计了一个级联的局部滤波器对图像的金字塔进行分类,从而把这种分类作为一个掩码来提取图像的反射率和阴影成分。文献[28]在本征分解中引入了基于纹理的非局部约束,假设空间上不相邻的像素,只要它们所在的图像块具有相似的纹理,具有相似反射率的可能性就更高。文献[29]在本征信息分解前,首先对像素进行聚类,并假设属于同一分割区域的像素具有相似的反射率。文献[30]引入点对的方式,构建全局约束项。全局/非局部约束更加符合自然图像的结构特性,相比于仅基于Retinex约束的方法,通常情况下能够获得更好的本征分解性能。
稀疏约束是稀疏表示理论在本征信息分解领域的成功应用。稀疏先验主要包含局部稀疏先验和全局稀疏先验。其中,局部稀疏先验假设是指在局部窗口内,两个像素点的色彩如果相似或相近,那它们通常具有相似的反射率,即反射率在局部窗口内具有稀疏特性。全局稀疏先验假设是指输入自然图像中色彩的种类其实也不多,而且色彩在图像中的分布具有结构性。换言之,自然图像中通常仅包含几种不同材质的物体,同一场景下不同反射率物体的数量具有稀疏性。稀疏先验是研究人员在大量观察和统计下发现的一种非常有效的图像先验,是本征信息分解问题求解的一种代表性手段。文献[31]提出了一种全局反射率稀疏性约束,假设每个自然图像只拥有为数不多的颜色,利用这种稀疏性先验和全局约束,进而制定了一个带约束L1范数最小化问题,可以有效地求解图像的本征信息。文献[32]充分利用反射率的结构相关性,采用了一个由较大邻域的双边核加权的非局部纹理先验,该先验与阴影的稀疏性先验相结合,可以恢复图像更精细的细节,同时不产生纹理伪影,且算法复杂度更低。
1.2.1.2 基于学习模型的方法经典的图像本征分解方法是从图像内部分解的角度来获取图像本征信息,为求解由原始图像得到反射和阴影成分的逆问题,常需要提供额外的约束或者先验知识。然而这些先验一般是人工假设的,无法充分完整地解释图像内部机理,在某些情况下会失效。因此有学者认为可以采用建立学习模型的方法直接预测像素间的亮度差异,而不是从图像像素光强中分离光照成分得到图像的物理本征反射率。这一灵感来源于人类视觉系统擅长在同一场景对两个不同空间位置的反射率进行可靠比较,通过对各图像块之间的相对反射率(“更亮”“更暗”“相同”)进行排序,从而生成一个反射率先验,再将该先验集成到现有的图像本征分解框架中即可实现对图像反射率的绝对估计。基于学习模型的方法完全不需要任何人工设计的先验,只有从数据中学习的隐性先验用于图像本征信息分解,较好地避免了由于人工干预带来的不适定问题。
随着人工智能与深度学习的快速发展,基于学习模型的方法为图像本征分解的经典问题开辟了探索领域。文献[33]首次使用复杂的深度特征和简单的局部分类规则来预测自然图像的亮度,采用稀疏编码策略与卷积神经网络相结合的方式输出跨越多个尺度的成对像素反射率差值,最终计算得到图像全局亮度排序。试验表明,该模型相比于包含多个阴影与反射率先验的全局亮度模型可以提供同等的性能。文献[34]训练了一个端到端的卷积神经网络预测成对像素间相对反射率的概率分布,然后将这种自主学习到的反射率先验输入全连接条件随机场中的能量最小化框架以获得原始图像的绝对反射率,即使在图像光照强度剧烈变化时,该方法的性能依然表现优秀。
目前基于学习模型的方法无法处理训练数据集中缺失的场景类型,而且常面临缺乏真值的问题。因此,如何面向开放的场景类型,并获取具有相对反射率标识的大规模数据集仍然是这一研究方向需要关注的两个重点问题。
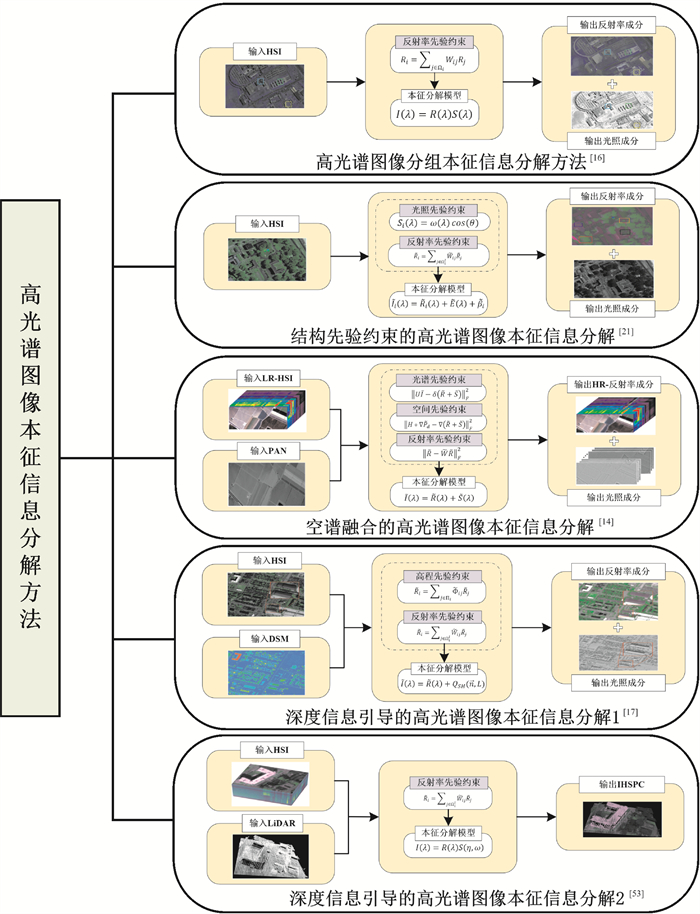
1.2.2 高光谱图像本征信息分解方法高光谱图像本征信息分解是高光谱遥感领域近年来出现的一项新兴技术。自文献[16]提出基于本征信息分解的高光谱图像特征提取方法以来,本征信息分解在高光谱遥感领域被赋予了新的内涵。与包含红、绿、蓝3个通道的彩色图像不同,高光谱图像是从可见光到红外数百个谱段图像构建的三维图像堆栈,既包含了丰富的空间结构也包含了精细的光谱信息。高光谱图像本征信息分解不仅仅是将输入图像分解为光照与颜色,同样也是将图像分解为与物体几何特性相关的空间光照图及与物体材质直接相关的光谱反射率图。高光谱图像的本征信息分解有望解耦高光谱图像最本征的空间与光谱信息,为“同物异谱”“异物同谱”这一高光谱遥感根本难题的解决提供了思路。现有的高光谱图像本征信息分解方法主要包括分组高光谱图像本征信息分解方法、结构先验约束的高光谱图像本征信息分解方法、空谱融合的高光谱图像本征信息分解方法及深度信息引导的高光谱图像本征信息分解方法。图 2为高光谱图像不同本征分解方法的模型及处理效果。
|
| 图 2 高光谱图像不同本征分解方法与处理效果 Fig. 2 Processing effects of different intrinsic decomposition methods for HSIs |
1.2.2.1 高光谱图像分组本征信息分解方法
高光谱图像分组本征信息分解将上百个谱段的高光谱图像本征分解问题转化为有限个彩色或多通道图像的本征分解问题。具体来说,该方法首先把高光谱图像I的特征维数降至B维,再将降维后的高光谱图像分解为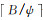
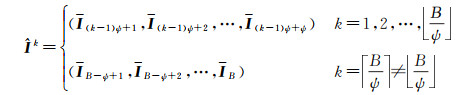 (7)
(7)
式中,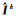
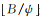
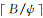
特征维数B与每组的波段数目ψ作为高光谱图像分组本征信息分解方法两个重要的参数,不同的参数设置将对算法性能产生不同的影响,在实际应用中通常需要使用部分真实数据集进行测试试验,尽可能地在高算法精度与低计算代价之间取得平衡,从而确定最佳参数值。在将一幅高光谱图像分为多个谱段子集后,理论上可以采用任意一种彩色图像本征分解方法同时处理各个谱段小组,最后将各组分解得到的相关成分合并即可获取整幅HSI图像的本征信息。文献[35]提出一种基于优化的本征图像分解方法,其基于局部窗口内具有相似亮度与相似色彩的图像往往具有相似光谱反射值的假设,将图像像素的反射成分建模为该像素邻域内像素反射成分的加权和
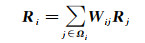 (8)
(8)
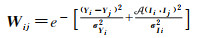 (9)
(9)
式中,Ωi是以像素i为中心的局部窗口;Wij为度量像素i和像素j在强度与光谱角两方面的相似度;Yi与Yj分别代表像素i与j内多个通道的平均强度值;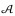
如果使用优化后的本征分解技术分别对每组的谱段子集进行图像本征分解,则第K组的反射成分Rk与光照成分Sk可以通过优化如下的能量函数[16]获得
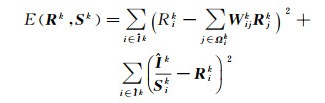 (10)
(10)
式中,等号右侧第一项为损失函数,表示像素i第k组波段反射成分与该像素邻域内像素对应波段反射成分的加权和之间的差值平方和;等号右侧第二项则代表像素i第k组波段反射成分与通过本征信息耦合模型计算出来的反射成分之间的差值平方和。由式(10)可以看出,能量函数E(Rk, Sk)越小,计算的反射成分Rk与光照成分Sk越准确。最后将获得的每个谱段子集的光谱反射成分合并,即可得到最终的光谱反射成分。
分组本征分解方法是一种通用的高光谱图像本征分解框架。几乎绝大多数的彩色图像本征分解方法均可以由分组求解的处理框架将其迁移至高光谱图像本征分解。该方法的优势是简单有效,缺点是并未充分考虑高光谱图像高维光谱信息的深层结构特性,因此在本征分解精度方面存在局限。
1.2.2.2 结构先验约束的高光谱图像本征信息分解经典的图像本征分解方法基于物理成像模型,通过去除阴影光照和恢复反射率成分,可以有效捕获原始图像中地物的特性,为后续图像解译等任务奠定分析基础。其中,建立反射率模型的关键在于提升其恢复精度的同时还要降低欠定问题的不确定性。对于HSI的本征分解模型而言,假设一幅HSI拥有d个波段,则每个像素将拥有2d个未知数,欠定问题的不确定性相比于RGB图像更加严重。一种常用且有效的解决方式是在某些先验条件下引入约束条件来减少不确定性,这里一般会用到两种先验:①引入光照先验以减少未知量的数量;②引入反射率先验,用来增加独立方程的数量。
光照先验描述了光照与物体表面之间的几何关系,可以有效地消除由于物体表面法线方向变化引起的反射率不均匀性。考虑到遥感场景中的光线来源于太阳光与大气层耦合后的结果,如果忽略光照的影响,此时可以认为整个空间的光线各向同性,光到达或离开目标表面的角度与波长λ无关,此时光照先验可以表示为[21]
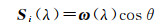 (11)
(11)
式中,θ为入射光方向ω与像素表面法向量n之间的夹角。该光照先验可以有效消除由物体表面法线方向变化,比如一栋房屋的向阳面与背阴面,而非物体材料变化引起的反射成分变化。为计算方便,在对数域中考虑式(11)可表达为
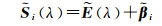 (12)
(12)
式中,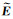
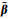
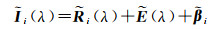 (13)
(13)
在该先验的约束条件下,未知数的总数从2du减少至(du+d+u)。
同样基于邻近像素往往具有相似反射率的先验,这里在对数域中考虑单个像素及其周围像素的反射率的关系式为
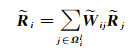 (14)
(14)
值得注意的是,该假设在大多数情况下都成立,但并不适用于图像边界上的像素,因为周围像素权重的引入会导致边界区域发生光谱混叠现象。有研究者提出利用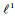
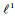
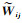
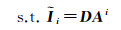 (15)
(15)
 (16)
(16)
式中,D为联合字典;Ai为稀疏系数矩阵,它度量了整张图像中除像素i外的所有像素描述像素i的能力,由此可以利用稀疏系数矩阵构建权重矩阵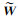
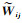
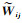
将光照先验与反射率先验结合在一起,可以得到基于结构先验约束的高光谱图像本征信息分解优化公式
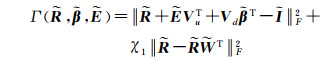 (17)
(17)
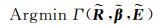 (18)
(18)
式中,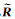
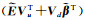
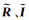
基于结构先验约束的高光谱图像本征信息分解作为一种早期的本征分解方法,优势在于简单易理解,计算复杂度不大,但由于先验来源于人为观察表象,难以捕捉到真实图像的物理内部规律,遇到某些比较特殊的图像时,可能会面临可解释性不强的困境。
1.2.2.3 空谱融合的高光谱图像本征信息分解高光谱图像本征信息分解对于改善高光谱领域的许多应用方法和技术起到了重要的作用,之前的研究专注于如何尽可能正确地捕获图像内部的本征信息,存在图像空间分辨率低的缺陷,影响主观视觉的传达与实际应用的定量分析效果。因此有研究者提出将低空间分辨率高光谱图像(low-spatial resolution hyperspectral image, LR-HSI)与全色(panchromatic,PAN)图像进行空谱融合,以增强本征成分的空间细节,克服HSI在空间分辨率方面受到限制的问题[14]。
基于空谱融合的高光谱图像本征信息分解方法关键在于如何在现有本征分解模型中引入PAN图像作为辅助数据,提升本征图像空间分辨率的同时又不影响从LR-HSI图像中分离出反射成分与光照成分。文献[14]在式(17)的基础上构造了3个合理的约束条件来解决这个问题。假设PAN图像为P,LR-HSI图像为I,P的总像素数量为u,I的通道数量为d。为方便表示,同样在对数域中考虑,则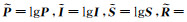
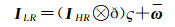 (19)
(19)
式中,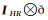
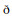
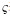
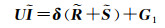 (20)
(20)
式中,U为双三次插值上采样算子;δ为模拟高光谱成像系统点扩散函数(the point spread function, PSF)的模糊算子,G1为加性噪声。根据式(20)得到第一项约束[14]
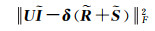 (21)
(21)
式中,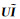
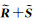
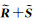
第二个约束从空间属性的角度来考虑,可以较好地保留图像的边缘细节。已知PAN图像具有高空间分辨率,且遥感图像的空间信息可以用梯度来度量[39],得到如下方程
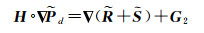 (22)
(22)
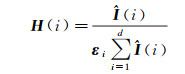 (23)
(23)
式中,“○”代表哈达玛积(Hadamard product); 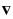
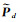
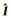
同理可以得到第二项空间约束[14]
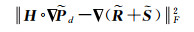 (24)
(24)
式中,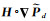
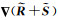
第三个约束与反射率有关,该约束同样基于反射分量在局部邻域具有强相关性的假设,如式(14)所示。这里假设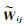
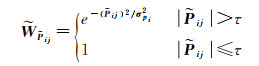 (25)
(25)
式中,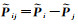
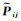
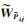
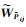
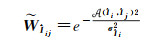 (26)
(26)
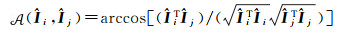 (27)
(27)
式中,
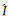
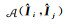
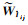
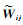
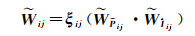 (28)
(28)
式中,ξ表示归一化系数。根据LR-HSI和PAN图像联合提供的相似度矩阵,可以更好地获取各像素反射率之间的关系。由此得到第三项反射率约束项为[14]
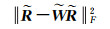 (29)
(29)
该约束项体现了用周围像素描述中心像素反射率的能力及分解出来的反射成分是否尽可能地满足对应的先验条件。
结合上述3个约束项,可以建立如下的能量函数[14]
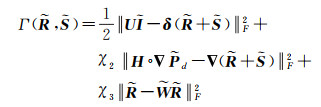 (30)
(30)
 (31)
(31)
式中,χ2和χ3分别决定两项约束项的权重。该优化函数通过进行多次迭代以寻找最小的Frobenius范数,最终收敛到E(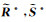
基于空谱融合的高光谱图像本征信息分解是研究者将图像本征分解技术进一步应用于实际的一种尝试,它通过图像融合与现有本征分解模型的巧妙结合实现了本征图像空间分辨率的进一步增强,有利于提升后续图像解译方法的性能。然而由于该方法基于多个人工假设来构造约束项,中间还涉及一些关键参数的选取,如何实现阈值参数的自动调整,提高计算效率是应用这项技术的必要考虑因素之一。
1.2.2.4 深度信息引导的高光谱图像本征信息分解通常情况下,高光谱图像本征信息分解是指从原始HSI图像中分离出反射和阴影成分,然而,关于“本征图像”问题,其更普遍的形式被描述为“几何、照明和反射”问题,即需要将光照成分进一步分解为几何和照明成分[24]。原因在于真实场景中光照并不总是均匀分布的,不同地物之间可能存在互相遮挡的关系,此时环境光照随空间地理位置变化,需要额外的先验知识以提出适当的约束条件来获取合理的图像本征分解结果。一些研究者已经尝试通过提供不同照度下的图像序列、场景深度信息、或入射光方向等手段来解决这一问题,其中基于深度信息引导的高光谱图像本征信息分解方法因其可以更准确地模拟物理成像过程,同时获取场景中包括坐标、高程、表面法线、光照和反射率等多个属性的优势受到了极大的关注[43-50]。
遥感领域常用到的携带场景深度信息的载体包括由卫星立体图像产生的数字表面模型(digital surface model, DSM)与激光雷达LiDAR点云。文献[17]利用DSM提供的几何信息成功地消除了由建筑物的阳面和阴面引起的本征反射率差异,且模型分解得到的反射率对光照变化的敏感性整体上都有所降低。与式(3)中表述光照成分的方法基本一致,光照成分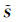
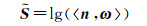 (32)
(32)
式中,n =[nx ny nz]T;ω =[ωx ωy ωz]T。由于上式涉及两个三维向量的点积的对数,为方便计算,本文采用式(5)的本征分解模型。取前两阶的球谐函数作为球谐基,L =[L1 L2 … L9]T是各个球谐基方向的系数,每一个参数都有其直观的物理含义。考虑到图像光照成分是由多个相互正交的球面谐波基函数叠加而成,因此可以在图像的不同空间位置控制L显示不同的图像亮度[51]。QSH(n, L)的具体计算公式为
 (33)
(33)
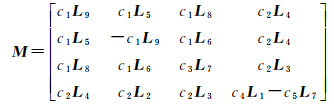 (34)
(34)
式中,c1, c2, …, c5均为常量。由于球面谐波基函数建立在法向量的基础上,这里需要利用DSM提供的深度信息来计算物体表面法线分布情况。DSM可以由一个u维向量Z =[Z1 Z2 … Zu]T表示,其中Zi是像素i处的高程,代入式(33)可得
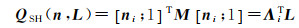 (35)
(35)
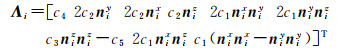 (36)
(36)
如果再定义一个几何分量J =[Λ1 Λ2 … Λu]T,即得到该本征分解模型的最终表达式
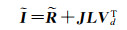 (37)
(37)
与之前的高光谱图像本征信息分解方法类似,该方法也引入了两项先验约束条件以解决本征分解问题的欠定性。第一项先验为反射率的局部先验,如式(14)所示。第二项先验为非局部先验,该先验基于拥有相似高程的像素通常具有相似反射率的假设。首先为每个像素建立一个(d+1)维向量。然后计算每个像素的特征向量之间的欧氏距离以找到该像素的全局k近邻Qig,并将其作为局部窗口Πi。该先验可以被描述为[52]
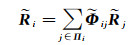 (38)
(38)
式中,稀疏矩阵Φ第i行第j列的元素Φij表示像素i和j在特征向量距离上的相似度。
综上可以得到最终的优化函数为
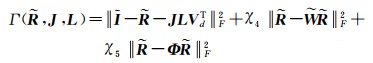 (39)
(39)
式中,χ4和χ5分别为两个约束项的权重。等号右侧第一项内容表示经本征分解后得到的反射、几何和照明成分叠加后得到的图像与原始图像之间的差距;等号右侧第二项和第三项反映了恢复后的反射成分服从对应先验约束的程度。通过对Γ进行全局最优搜索,当Γ最小时,即可获得相对最准确的反射率成分。
不同于DSM等二维图像,LiDAR通过对地表进行密集的三维激光扫描,可以获取立体几何信息丰富的三维点云数据,其与高光谱数据存在高度互补性。文献[53]通过建立HSI和LiDAR的联合本征分解框架,可以输出同时拥有三维坐标、表面法线和反射率的本征高光谱点云(intrinsic hyperspectral point cloud, IHSPC)。为了完整保留点云中包含的不规则三维信息,该方法提出一种专门用于HSI和LiDAR的本征场景模型(intrinsic scene model, ISM),实现了从三维点云到二维HSI像素的本征映射,有效恢复了包括三维高光谱反射率和环境光照等在内的多个本征属性。
ISM模型首先将双向反射率分布函数(bidirectional reflectance distribution function, BRDF)应用于HSI的每个像素以获取亚像素的反射率和几何形状,再基于几何的蒙特卡罗采样推导出模型的离散形式,从而将具有不同数据结构和分辨率的HSI和LiDAR对应起来。假设HSI第i个像素为Ii,LiDAR点云中对应像素Ii的点子集为{Θij}j=1Q,Q为点的个数。根据ISM模型,Ii可以被LiDAR点子集Θ描述为
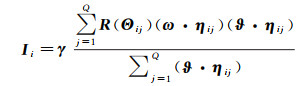 (40)
(40)
式中,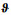
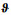
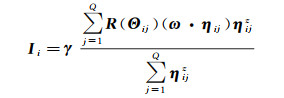 (41)
(41)
由于物体材质和表面法线方向的变化都会导致HSI像素强度的变化,为保证表面法线方向的变化是HSI图像强度变化的唯一变量,对LiDAR点云进行聚类分割。对于相同类别的像素,可以得到一组方程
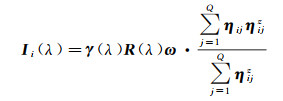 (42)
(42)
式中,λ为波长;{ηij}j=1Q为LiDAR点云子集的法线,提供了HSI像素k包含的亚像素形状信息。根据式(3)的本征分解模型,S(η, ω) 可由以下亚像素模型表示
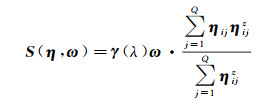 (43)
(43)
为求解该分解模型的逆问题,同样引入如式(7)所示的局部反射率先验,使用基于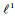
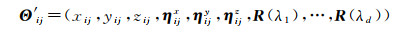 (44)
(44)
式中,(xij, yij, zij)分别为点Θ′i在x, y, z方向的坐标;R(λ1), R(λ2), …, R(λd)为该点在每个波长处的反射率。
深度信息的引入给高光谱图像本征信息分解领域带来了机遇,其恢复的场景本征属性有利于人们更加直观地理解真实的物理世界。然而目前将这项技术应用于实际还存在一些困难,如考虑到LiDAR点云的量级为百万甚至千万级别,在每个点上完成本征分解和优化任务是相当具有挑战性的。尽管文献[54]已经提出使用加权图聚类的方式将LiDAR点云分割成超体素以降低计算复杂度,但如何优化现有的框架以尽可能地缩短数据处理时间仍值得被持续关注[54]。
总体来看,上述4种具有代表性的高光谱本征信息分解方法各有优缺点,其优缺点及使用的数据源见表 1。
| 高光谱本征信息分解方法 | 优点 | 缺点 | 数据源 |
| 高光谱图像分组本征信息分解方法 | 通用性强,简单有效 | 未充分考虑高光谱图像高维光谱信息的深层结构特性 | the Indian Pines image(https://purr.purdue.edu/publications/1947/1);the University of Pavia image(https://www.ehu.eus/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes);the Salinas image(https://www.ehu.eus/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes) |
| 结构先验约束的高光谱图像本征信息分解 | 容易理解,计算复杂度不大 | 先验条件来源于人为观察表象,难以解释性能波动现象 | the Indian Pinesimage;MUUFL Gulfport(http://engineers.missouri.edu/zarea/2013/10/muuflgulfport-hyperspectral-and-lidar-data-collection/);University of Houston [55] |
| 空谱融合的高光谱图像本征信息分解 | 进一步提升了高光谱本征图像的空间分辨率 | 基于多个人工假设,关键参数较多,依赖人工调参 | the Salinas image;the Botswana image(https://www.ehu.eus/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes);the Yellow Riverimage (http://data.cresda.com) |
| 深度信息引导的高光谱图像本征信息分解 | 为高光谱本征图像额外补充了深度信息 | 数据量大,数据处理时间较长 | 基于2018 IEEE GRSS Data Fusion Contest “grss_dfc_2018” dataset合成的高光谱点云[56](http://www.grss-ieee.org/community/technical-committees/data-fusion) |
2 高光谱图像本征信息分解的挑战及未来发展方向
图像本征信息分解技术在计算机视觉领域发展由来已久,但专门针对其在遥感高光谱领域的应用研究工作还远远不够。前人已经尝试从不同的方法论角度,如分组分解、基于不同先验约束、空谱融合和基于深度信息引导等方面提出了多种本征信息耦合模型和本征信息分解方法,带领该技术朝着兼具创新性与实用性的方向迈出了坚实的一步。但考虑到现实情境的复杂性与应用范围的广泛性,将高光谱图像本征信息分解大范围且高效地应用于实际仍然存在以下几个亟待解决的关键问题与挑战。
2.1 复杂成像环境下的本征信息分解由于高光谱图像为卫星或无人机从高空中远距离拍摄,图像覆盖的地面区域面积甚广,且涉及的地表类型颇为丰富。但由于光学遥感成像环境十分复杂,获取的高光谱图像可能会受到一些无法人为控制甚至难以避免的物理现象或环境的影响,而这些因素对于实现高光谱图像本征信息精确分解造成了一定的阻碍。从拍摄场景来看,例如烈阳下的海面有明显的耀斑,反射率过高的建筑物材料等一切会造成镜面反射的目标都会导致图像出现过度曝光现象;从图像传输过程的角度来看,不同的天气状况会导致辐射能量具有不同程度的衰减,云层阻挡太阳辐射会带来大面积的连续阴影;从最终成像的角度来看,传感器内部不可避免地会存在各种噪声,生成的图像也会存在一定程度的空间几何畸变与光谱畸变。面向复杂场景的高光谱图像本征信息分解理论模型已将这些变化因素考虑在内,然而由于不同的外界干扰对高光谱图像的影响方式不同,意味着需要深入研究每一种变化因素对高光谱图像的干扰机理,探索形成集生成-传输-获取全链路的本征信息耦合模型,这是现有关于高光谱图像本征信息分解研究工作所欠缺的。此外,在该模型的基础上,有必要设计环境自适应的本征信息分解与提取处理流程与框架,以提升高光谱图像本征信息分解的适用性与稳健性。
2.2 亚像元目标的本征空谱信息提取由于受到高光谱图像空间分辨率的固有限制及复杂地物分布情况的影响,遥感影像上很少存在纯净像元,特别对于尺寸微小的目标物体而言,它很难占满一个像元的全部面积,更多的情况是目标物体与其他多种地物共同组成混合像元。此时待探测目标存在于亚像元中,对应的问题转化为在像元内部检测甚至定位目标存在与否的亚像元小目标探测问题。对于高光谱图像本征信息分解而言,传统的先验约束条件已经不适用于这类亚像元的目标,一种可能的技术解决方案是将前沿的高光谱图像光谱解混或超分辨率技术与本征分解方法相结合,实现亚像元目标的本征空谱信息提取,从而为提高遥感精细化分类水平及目标探测精度提供更大的可能性。目前关于图像本征分解与超分技术的结合已经有一些成功的尝试,但在这一方向上仍需要付出更多的努力[53-54]。
2.3 高光谱图像本征空谱信息融合从高光谱图像本征信息分解这项研究工作的动机出发,准确提取并表征物体最本征的光谱与空间信息是它的直接目的,但究其本质仍旧在于提升高光谱图像的识别与解译性能。对于现有的高光谱图像本征分解方法而言,其涉及的下游应用绝大多数仅限于地物分类,且下意识地只利用了分解出来的单一光谱反射成分,忽略了其他本征成分也可能给模型带来有用信息的事实。为挖掘该技术更大的应用潜力,可以考虑将分解出来的光谱反射成分、光照成分及其他本征成分联合使用,实现高光谱图像本征空谱信息融合,以便进一步拓展后续模型的使用范围同时提升相应模型的性能。
2.4 多时相高光谱本征图像分解受到某些自然因素如太阳高度角、大气、环境、地形、物候及物种疾病的影响,探测到的物体光谱特征会随时间发生变化,只从单幅图像中提取的本征反射率图像可能与所需的物体真实本征信息存在一定偏差,从而影响后续的图像解译工作,因此有必要研究面向多时相高光谱图像的本征分解方法,解决因光谱变化引起同一地物在不同时段光谱数据分布不一致的问题。文献[57]提出一种具有变化检测能力的高光谱多时相图像本征分解方法,试验结果表明该方法在反射率提取、多时相高光谱图像分类和变化检测精度方面都优于传统方法,但仍存在一些缺陷。例如,该方法无法处理多幅不同时相的高光谱图像且存在算法耗时长的缺点。未来针对多时相高光谱图像的本征分解方法可以尝试针对上述难题做出改进,从而有效提高目前多时相高光谱本征图像分解方法的本征信息定量提取准确性、应用广泛性与实际可行性。此外,利用多帧图像的额外信息对高光谱视频进行本征信息提取也是一个值得探索的新的方向。
2.5 基于本征信息分解的高光谱图像样本生成随着人工智能技术的发展,深度学习在目标检测、图像分割及自然语言处理等研究领域大放异彩,其与遥感高光谱领域的深度交叉融合也掀起了一波研究热潮。在使用大数据训练模型的趋势下,深度神经网络因其强大的学习能力与泛化能力在遥感高光谱领域的众多应用中已取得了显著的效果。然而使用高光谱图像作为训练样本存在一个天然的劣势,即标注样本过少,难以支撑大规模学习模型的样本需求,而人力标注费事费力,一定程度上提高了深度学习在高光谱影像应用中的门槛。发展基于本征信息分解的高光谱图像样本生成研究有助于模拟出更真实的高光谱样本,例如在纯净的本征图像上叠加不同的光照条件以生成不同的图像序列,或借助于其物理生成机理与其他深度生成模型相结合产生更高质量、更多数量的样本,从而成为解决这一难点问题的可行办法。同时,该样本生成方法的另一个好处在于生成的样本具有物理可解释性,因此可以在可控的范围内对生成的图像进行任意的调整操控,对理解后续黑箱模型的物理意义及各种参数的使用也起到了一定的辅助和指导作用。
2.6 多模态遥感图像本征信息的提取与融合目前提出的高光谱图像本征信息耦合模型大多集中在提取出高光谱图像的光谱反射成分、光照成分及空间几何成分,从系统应用的视角出发,高光谱图像作为一种单一模态,其获取的本征信息即使再准确也难以避免存在片面性。安装在同一平台上的不同载荷输出不同模态的图像数据,天然地为实现互补信息融合提供了极佳的硬件基础。因此,为获取更加全面丰富的地物信息,有必要挖掘不同模态图像最本征的信息,如热红外图像具有的辐射信息、雷达图像具有的高分辨几何信息等,这首先需要针对不同的模态图像建立合理的本征信息耦合模型,在提取相应的本征信息后再进行进一步的融合。值得注意的是,建立多模态遥感图像本征信息耦合模型这一步本身比较困难,因为这需要对各个模态图像的生成机理、内部规律与表现形式具有极深层次的理解与把握才能实现,而这依赖于所有致力于从事这一研究方向的科研人员的支持与贡献。
2.7 多平台高光谱图像本征信息分解高光谱图像的来源分为航天、航空与地面高光谱成像平台,不同成像平台在拍摄条件、环境噪声、观测视角、数据传输链路及图像分辨率等方面都面临着很大差异。绝大多数高光谱图像本征信息分解方法仅在机载数据集上进行了验证,没有提及其他平台数据集的适用情况。然而文献[14]将基于空谱融合的高光谱图像本征信息分解方法同时应用于机载数据集与星载数据集上且都取得了不错的效果,证明高光谱图像本征信息分解在不同平台数据上均具有较好的应用潜力。未来的高光谱图像本征信息分解方法可以将高光谱图像来源考虑在内,针对不同平台设计针对性的本征信息分解方法,并在多平台数据集上进行验证。
2.8 高光谱图像本征分解信息应用现有的高光谱图像本征分解工作大多专注于提出一些高光谱本征分解框架,最后在公共分类数据集上验证该本征分解方法的性能优劣,没有将分解后得到的本征图像进一步推广至现实场景应用。一些研究者已经证实相比于高光谱原始图像,高光谱本征图像在矿物勘探、变化检测领域都为解译模型带来了性能上的提升,但在军事侦察等其他领域暂时还未出现高光谱本征图像的应用先例[57-58]。为进一步促成科研成果的高效转化落地,有必要围绕下游应用开展高光谱图像本征信息分解研究,贴合实际场景对本征分解方法进行适应性改进,从而较大限度地发挥高光谱图像本征信息分解方法的潜能。
3 结论高光谱图像本征信息分解作为计算机视觉领域与遥感高光谱领域交叉融合的又一成功案例,可以去除因光照不均等因素对高光谱图像的影响,提取地物纯净光谱反射特征,获得辨识度更高的本征光谱反射率图像。由于其处于技术管道的上游,因此理论上几乎可以与后续所有的应用算法结合以进一步提升模型性能。本文综述了现有的主流高光谱本征分解耦合模型,总结了基于分组分解、基于结构先验约束、基于空谱融合及基于深度信息引导的4类高光谱图像本征信息分解方法的基本原理与各自的优缺点,最后讨论了目前高光谱图像本征信息分解领域面临的主要挑战与未来的发展方向。可以预计,未来几年基于高光谱图像本征信息分解的创新研究与实际应用将持续增长,期盼本文为希望进一步探索开发高光谱图像本征信息分解方法的研究人员提供新的启发与动力。
| [1] |
赵英时. 遥感应用分析原理与方法[M]. 北京: 科学出版社, 2003: 34-37. ZHAO Yingshi. Principles and methods of remote sensing application analysis[M]. Beijing: Science Press, 2003: 34-37. |
| [2] |
HU X, XIE C, FAN Z, et al. Hyperspectral anomaly detection using deep learning: a review[J]. Remote Sensing, 2022, 14(9): 1973. DOI:10.3390/rs14091973 |
| [3] |
JIA J, WANG Y, CHEN J, et al. Status and application of advanced airborne hyperspectral imaging technology: a review[J]. Infrared Physics and Technology, 2020, 104: 103115. DOI:10.1016/j.infrared.2019.103115 |
| [4] |
QIAN S. Hyperspectral satellites, evolution, and development history[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2021, 14: 7032-7056. DOI:10.1109/JSTARS.2021.3090256 |
| [5] |
LU B, DAO P D, LIU J, et al. Recent advances of hyperspectral imaging technology and applications in agriculture[J]. Remote Sensing, 2020, 12(16): 2659. DOI:10.3390/rs12162659 |
| [6] |
LU L, GONG Z, LIANG Y, et al. Retrieval of chlorophyll-a concentrations of class Ⅱ water bodies of inland lakes and reservoirs based on ZY1-02D satellite hyperspectral data[J]. Remote Sensing, 2022, 14(8): 1842. DOI:10.3390/rs14081842 |
| [7] |
ZHANG B, GUO B, ZOU B, et al. Retrieving soil heavy metals concentrations based on GaoFen-5 hyperspectral satellite image at an opencast coal mine, Inner Mongolia, China[J]. Environmental Pollution, 2022, 300: 118981. DOI:10.1016/j.envpol.2022.118981 |
| [8] |
SHIMONI M, HAELTERMAN R, PERNEEL C. Hyperspectral imaging for military and security applications: combining myriad processing and sensing techniques[J]. IEEE Geoscience and Remote Sensing Magazine, 2019, 7(2): 101-117. DOI:10.1109/MGRS.2019.2902525 |
| [9] |
刘冰, 左溪冰, 谭熊, 等. 高光谱影像分类的深度少样例学习方法[J]. 测绘学报, 2020, 49(10): 1331-1342. LIU Bing, ZUO Xibing, TAN Xiong, et al. A deep few-shot learning algorithm for hyperspectral image classification[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(10): 1331-1342. DOI:10.11947/j.AGCS.2020.20190486 |
| [10] |
孙一帆, 余旭初, 谭熊, 等. 面向小样本高光谱影像分类的轻量化关系网络[J]. 武汉大学学报信息科学版, 2022, 47(8): 1336-1348. SUN Yifan, YU Xuchu, TAN Xiong, et al. Lightweight relational network for small sample hyperspectral image classification[J]. Geomatics and Information Science of Wuhan University, 2022, 47(8): 1336-1348. |
| [11] |
XUE Z, NIE X. Low-rank and sparse representation with adaptive neighborhood regularization for hyperspectral image classification[J]. Journal of Geodesy and Geoinformation Science, 2022, 5(1): 73. DOI:10.11947/j.JGGS.2022.0108 |
| [12] |
WANG K, ZHENG S, RUI L, et al. A deep double-channel dense network for hyperspectral image classification[J]. Journal of Geodesy and Geoinformation Science, 2021, 4(4): 46-62. DOI:10.11947/j.JGGS.2021.0404 |
| [13] |
任智伟, 吴玲达. 基于本征图像分解的高光谱图像空谱联合分类[J]. 航天返回与遥感, 2019, 40(3): 111-120. REN Zhiwei, WU Lingda. Spectral-spatial classification for hyperspectral imagery based on intrinsic image decomposition[J]. Spacecraft Recovery and Remote Sensing, 2019, 40(3): 111-120. DOI:10.3969/j.issn.1009-8518.2019.03.014 |
| [14] |
GU Y, XIE W, LI X, et al. Hyperspectral intrinsic image decomposition with enhanced spatial information[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5523014. |
| [15] |
BARROW H, TENENBAUM J, HANSON A, et al. Recovering intrinsic scene characteristics[J]. Computer Vision Systems, 1978, 2: 3-26. |
| [16] |
KANG X, LI S, FANG L, et al. Intrinsic image decomposition for feature extraction of hyperspectral images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(4): 2241-2253. DOI:10.1109/TGRS.2014.2358615 |
| [17] |
JIN X, GU Y, XIE W. Intrinsic hyperspectral image decomposition with DSM cues[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 60: 1-13. |
| [18] |
GAO G, LIU B, ZHANG X, et al. Multitemporal intrinsic image decomposition with temporal-spatial energy constraints for remote sensing image analysis[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 60: 1-16. |
| [19] |
HUANG Q, ZHU W, ZHAO Y, et al. Multispectral image intrinsic decomposition via subspace constraint[C]//Proceedings of 2018 IEEE Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 6430-6439.
|
| [20] |
JIN X, GU Y. Superpixel-based intrinsic image decomposition of hyperspectral images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(8): 4285-4295. DOI:10.1109/TGRS.2017.2690445 |
| [21] |
JIN X, GU Y, LIU T. Intrinsic image recovery from remote sensing hyperspectral images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 57(1): 224-238. |
| [22] |
BARRON J T, MALIK J. Shape, illumination, and reflectance from shading[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(8): 1670-1687. DOI:10.1109/TPAMI.2014.2377712 |
| [23] |
BARRON J T, MALIK J. High-frequency shape and albedo from shading using natural image statistics[C]//Proceedings of 2011 IEEE Conference on Computer Vision and Pattern Recognition. Colorado: IEEE, 2011: 2521-2527.
|
| [24] |
BARRON J T, MALIK J. Shape, albedo, and illumination from a single image of an unknown object[C]//Proceedings of 2012 IEEE Conference on Computer Vision and Pattern Recognition. Rhode Island: IEEE, 2012: 334-341.
|
| [25] |
LAND E H, MCCANN J J. Lightness and retinex theory[J]. Josa, 1971, 61(1): 1-11. DOI:10.1364/JOSA.61.000001 |
| [26] |
GROSSE R, JOHNSON M K, ADELSON E H, et al. Ground truth dataset and baseline evaluations for intrinsic image algorithms[C]//Proceedings of 2009 IEEE International Conference on Computer Vision. Kyoto: IEEE, 2009: 2335-2342.
|
| [27] |
BELL M, FREEMAN E T. Learning local evidence for shading and reflectance[C]//Proceedings of 2001 IEEE International Conference on Computer Vision. Columbia: IEEE, 2001: 670-677.
|
| [28] |
SHEN L, TAN P, LIN S. Intrinsic image decomposition with non-local texture cues[C]//Proceedings of 2008 IEEE Conference on Computer Vision and Pattern Recognition. Alaska: IEEE, 2008: 1-7.
|
| [29] |
GARCES E, MUNOZ A, LOPEZ-MORENO J, et al. Intrinsic images by clustering[C]//Proceedings of 2012 Computer Graphics Forum. Oxford: Blackwell Publishing Ltd, 2012, 31(4): 1415-1424.
|
| [30] |
CHEN Q, KOLTUN V. A simple model for intrinsic image decomposition with depth cues[C]//Proceedings of 2013 IEEE International Conference on Computer Vision. Sydney: IEEE, 2013: 241-248.
|
| [31] |
SHEN L, YEO C, HUA B S. Intrinsic image decomposition using a sparse representation of reflectance[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(12): 2904-2915. DOI:10.1109/TPAMI.2013.136 |
| [32] |
LI K, WANG Y, YE X, et al. Sparse intrinsic decomposition and applications[J]. Signal Processing: Image Communication, 2021, 95: 116281. DOI:10.1016/j.image.2021.116281 |
| [33] |
NARIHIRA T, MAIRE M, YU S X. Learning lightness from human judgement on relative reflectance[C]//Proceedings of 2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston: IEEE, 2015: 2965-2973.
|
| [34] |
ZHOU T, KRAHENBUHL P, EFROS A A. Learning data-driven reflectance priors for intrinsic image decomposition[C]//Proceedings of 2015 IEEE International Conference on Computer Vision. Chile: IEEE, 2015: 3469-3477.
|
| [35] |
SHEN J, YANG X, Li X, et al. Intrinsic image decomposition using optimization and user scribbles[J]. IEEE Transactions on Cybernetics, 2013, 43(2): 425-436. DOI:10.1109/TSMCB.2012.2208744 |
| [36] |
CHENG B, YANG J, YAN S, et al. Learning with L1-graph for image analysis[J]. IEEE Transactions on Image Processing, 2010, 19(4): 858-866. DOI:10.1109/TIP.2009.2038764 |
| [37] |
KAROUI M S, DEVILLE Y, BENHALOUCHE F Z, et al. Hypersharpening by joint-criterion nonnegative matrix factorization[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(3): 1660-1670. DOI:10.1109/TGRS.2016.2628889 |
| [38] |
ZHANG K, ZUO W, ZHANG L. Learning a single convolutional super-resolution network for multiple degradations[C]//Proceedings of 2018 IEEE Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 3262-3271.
|
| [39] |
PIELLA G. Image fusion for enhanced visualization: avariational approach[J]. International Journal of Computer Vision, 2009, 83(1): 1-11. DOI:10.1007/s11263-009-0206-4 |
| [40] |
AIAZZI B, ALPARONE L, BARONTI S, et al. MTF-tailored multiscale fusion of high-resolution ms and pan imagery[J]. Photogrammetric Engineering and Remote Sensing, 2006, 72(5): 591-596. DOI:10.14358/PERS.72.5.591 |
| [41] |
RUBIN J M, RICHARDS W A. Color vision and image intensities: when are changes material?[J]. Biological Cybernetics, 1982, 45(3): 215-226. DOI:10.1007/BF00336194 |
| [42] |
MOREL J M, PETRO A B, SBERT C. A PDE formalization of retinex theory[J]. IEEE Transactions on Image Processing, 2010, 19(11): 2825-2837. DOI:10.1109/TIP.2010.2049239 |
| [43] |
LI Z, SNAVELY N. Learning intrinsic image decomposition from watching the world[C]//Proceedings of 2018 IEEE Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 9039-9048.
|
| [44] |
KONG N, BLACK M J. Intrinsic depth: improving depth transfer with intrinsic images[C]//Proceedings of 2015 IEEE International Conference on Computer Vision. Chile: IEEE, 2015: 3514-3522.
|
| [45] |
HACHAMA M, GHANEM B, WONKA P. Intrinsic scene decomposition from RGB-D images[C]//Proceedings of 2015 IEEE International Conference on Computer Vision. Chile: IEEE, 2015: 810-818.
|
| [46] |
LAFFONT P Y, BAZIN J C. Intrinsic decomposition of image sequences from local temporal variations[C]//Proceedings of 2015 IEEE International Conference on Computer Vision. Chile: IEEE, 2015: 433-441.
|
| [47] |
JEON J, CHO S, TONG X, et al. Intrinsic image decomposition using structure-texture separation and surface normals[C]//Proceedings of 2014 European Conference on Computer Vision. Switzerland: Springer, 2014: 218-233.
|
| [48] |
YU L F, YEUNG S K, TAI Y W, et al. Shading-based shape refinement of RGB-D images[C]//Proceedings of 2013 IEEE Conference on Computer Vision and Pattern Recognition. Portland: IEEE, 2013: 1415-1422.
|
| [49] |
BARRON J T, MALIK J. High-frequency shape and albedo from shading using natural image statistics[C]//Proceedings of 2011 IEEE Conference on Computer Vision and Pattern Recognition. Colorado Springs: IEEE, 2011: 2521-2528.
|
| [50] |
BASRI R, JACOBS D W, EMELMACHER I K. Photometric stereo with general, unknown lighting[J]. International Journal of Computer Vision, 2007, 72(3): 239-257. DOI:10.1007/s11263-006-8815-7 |
| [51] |
RAMAMOORTHI R, HANRAHAN P. An efficient representation for irradiance environment maps[C]//Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM Press, 2001: 497-500.
|
| [52] |
CHOMBOON K, CHUJAI P, TEERARASSAMEE P, et al. An empirical study of distance metrics for k-nearest neighbor algorithm[C]//Proceedings of the 3rd International Conference on Industrial Application Engineering. Kitakyushu: ⅡAE, 2015: 280-285.
|
| [53] |
JIN X, GU Y. Intrinsic scene properties from hyperspectral images and LiDAR[C]//Proceedings of 2019 IEEE Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019: 1423-1431.
|
| [54] |
JIN X, GU Y, LIU T, et al. Supervoxel-based intrinsic scene properties from hyperspectral images and LiDAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 60: 1-13. |
| [55] |
DEBES C, MERENTITIS A, HEREMANS R, et al. Hyperspectral and LiDAR data fusion: outcome of the 2013 GRSS data fusion contest[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(6): 2405-2418. DOI:10.1109/JSTARS.2014.2305441 |
| [56] |
XU Y, DU B, ZHANG L, et al. Advanced multi-sensor optical remote sensing for urban and use and land cover classification: outcome of the 2018 IEEE GRSS data fusion contest[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2019, 12(6): 1709-1724. DOI:10.1109/JSTARS.2019.2911113 |
| [57] |
GAO G, LIU B, ZHANG X, et al. Multitemporal intrinsic image decomposition with temporal-spatial energy constraints for remote sensing image analysis[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 60: 1-16. |
| [58] |
DUAN P, LAI J, GHAMISI P, et al. Component decomposition-based hyperspectral resolution enhancement for mineral mapping[J]. Remote Sensing, 2020, 12(18): 2903. DOI:10.3390/rs12182903 |



