2. 国家地理信息系统工程技术研究中心, 湖北 武汉 430078;
3. 中国地质大学(武汉)地质探测与评估教育部重点实验室, 湖北 武汉 430074;
4. 湖北省地质环境总站, 湖北 武汉 430034;
5. 中国地质大学(武汉)地理与信息工程学院, 湖北 武汉 430078;
6. 西安测绘研究所, 陕西 西安 710054;
7. 地理信息工程国家重点实验室, 陕西 西安 710054
2. National Engineering Research Center of Geographic Information System, Wuhan 430078, China;
3. Key Laboratory of Geological Survey and Evaluation of Ministry of Education, China University of Geosciences, Wuhan 430074, China;
4. Geological Environmental Center of Hubei Province, Wuhan 430034, China;
5. School of Geography and Information Engineering, China University of Geoscience, Wuhan 430078, China;
6. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China;
7. State Key Laboratory of Geo-Information Engineering, Xi'an 710054, China
越野环境下的路径规划起初应用于军事领域,通过对战场环境的分析,指挥机动车辆、人员在战场中的行动[1-5],随着科学技术的不断进步、人类需求的不断提高,其逐渐应用于民用交通、抗震救灾及民事生产等民生领域[6-10]。特别是近些年自然灾害增多,灾区救援争分夺秒,尽早规划出通往灾区的可通行路径对救援十分必要[11]。越野环境地域广阔,地势起伏不定,地表覆盖类型多样,目前多数研究主要考虑环境因素约束,而路径规划问题通常还存在有限的处理时间、内存和计算能力等性能约束,伴随着规划区域的扩大,通行模型数据规模增加,路径规划效率受限[12-13]。因此,如何在大规模越野场景中实现顾及多种环境因素约束的高效率越野路径规划方法就成为本文的研究重点。
通行环境场景建模是越野路径规划的基础,将复杂的野外通行环境量化为路径规划算法所需要的影响因子,便于算法感知通行环境[14]。通行模型常用拓扑法、栅格法、可视图法和构型空间法等构建,其中栅格法使用简单,可以同时对不规则的障碍物进行表达,能够处理较为复杂的越野环境情况,也便于对多种影响因素进行叠加分析计算,本文也采用栅格法构建通行模型[15-16]。栅格单元形状一般为正三角形、正四边形和正六边形3种,在越野环境中,通行对象运动没有路网的约束,前进方向多样,因此具有更多通行方向、更一致领域关系的六角格网更适用于越野通行环境场景建模[17]。通行模型格网数据规模的增大会严重影响路径规划算法的计算效率,六角格网相较于三角和四角格网,拥有更高的平面覆盖率,使用六角格网作为栅格形状可以相对减少通行模型格网数量[18]。但对于大范围的通行模型构建,格网数据规模依旧是巨大的,路径规划效率仍会陷入瓶颈。为了解决这类问题,文献[19—21]提出应用层次空间推理思想,将大规模路网进行分级或分层处理,缩减问题空间,利用“分而治之”的方法,将问题细分求解,有效缓解了路径规划在大规模路网中效率低下的问题。然而越野场景通常路网稀疏,不能依靠路网层次结构对其进行分层处理以降低数据规模,提升规划效率。据此,本文充分发挥层次空间推理思想在问题规模缩减方面的作用,在区域广阔的无路网野外环境中,依靠多层次格网剖分系统构建多层次六角格网通行模型,减少格网数据规模,提升路径规划效率。
越野环境路径规划算法需要有效兼顾多种约束条件并具有良好的运行效率,目前常用算法主要包括Dijkstra算法、A*算法、蚁群算法、遗传算法和粒子群算法等[22]。其中A*算法作为启发式搜索算法,可以将约束条件作为启发因素,缩小搜索范围以提高算法效率,常被应用于需要考虑多约束条件的越野路径规划,本文也采用A*算法进行路径规划[23]。算法核心在于如何将选取合适的启发因素,以得到合理的代价估计。文献[24—25]将地形坡度、地表覆盖等多种环境影响因子作为算法启发因素,有效模拟真实越野环境,提升路径规划效率。据此,本文提出一种面向越野路径规划的多层次六角格网通行模型,该模型由普通六角格网通行模型,历经多层次格网压缩及邻接关系重构生成。同时,本文在A*算法的基础上,依据通行模型格网的多层次特点,针对通行环境中的各种约束条件优化其启发函数,构建适用于大规模越野场景的路径规划算法。基于此模型,本文以地形和地表覆盖类型为例,选取遍历格网数、路径格网数及算法执行时间等8个指标,在算法运行效率和算法可靠性两个方面进行对比试验,说明本文提出的多层次六角格网通行模型相较于普通六角格网通行模型能够有效缩减格网数据规模,保持规划路径质量,提升路径规划效率。
1 多层次六角格网通行模型的构建普通六角格网通行模型的构建是生成多层次通行模型的前提。以格网地图为基础,结合影响因子量化生成的通行能力,构建出普通六角格网通行模型,经格网层次压缩及邻接关系重构生成多层次通行模型。由于多层次通行模型与普通六角格网通行模型的格网地图结构不同,所以还需要优化路径规划算法使其适配多层次通行模型,流程图如图 1所示。
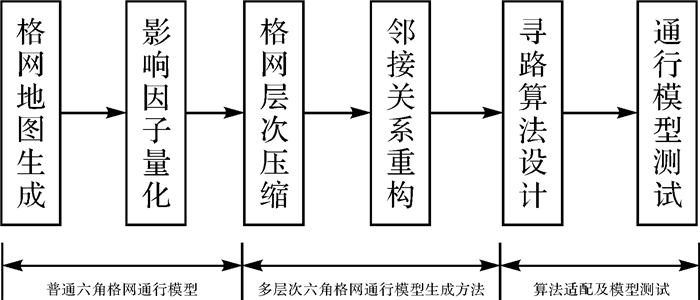
|
| 图 1 多层次六角格网通行模型生成技术路线 Fig. 1 Multi-hierarchy hexagonal grid traffic model generation technical route |
1.1 普通六角格网通行模型
通行模型的构建首先须生成格网地图,然后分析量化影响因子,为格网赋予相应的通行能力。
1.1.1 六角格网地图生成格网地图通常由形状为正三角形、正四边形或正六边形的格网组成,适用于不同的应用场景[26-27]。如图 2所示,正六边形与相邻格网只有1种邻接关系且有6个通行方向,正三角形有2种邻接关系和6个通行方向,正四边形有2种邻接关系与8个通行方向。在路径规划中,由于正六边形具有更一致的邻接关系,拥有更多的等距通行方向个数,方便算法处理邻接关系,利于影响因子量化,因此,本文采用正六边形作为格网地图中的格网形状。
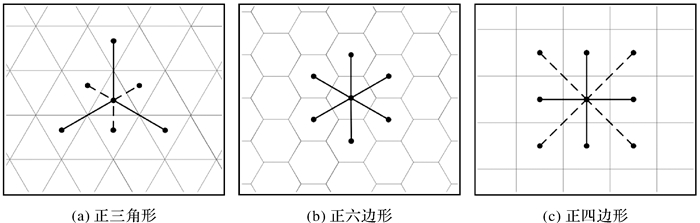
|
| 图 2 3种多边形邻接关系与通行方向 Fig. 2 Adjacency relation and passage direction of three polygons |
本文参照开源算法Uber-H3[28]构建了多层次格网剖分系统,如图 3所示。在该系统中,任意一个地理坐标在每个格网层次中都具有唯一的格网索引与之相对应,通过格网索引可以获取到任意格网的邻接格网,不同层次的格网在范围上具有上下层涵盖关系。
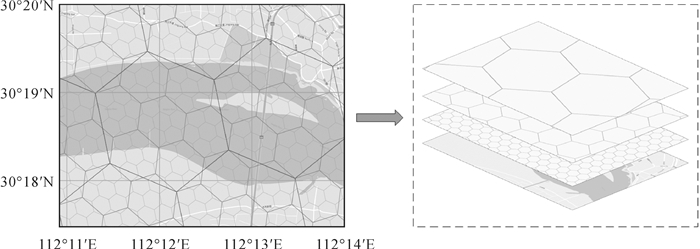
|
| 图 3 多层次格网剖分系统 Fig. 3 Hierarchy grid system |
1.1.2 影响因子量化
影响因子量化是对影响通行对象通行的地质地形要素进行分析,用于对复杂丰富的越野环境进行抽象和简化,以实现对实际地质地形的量化模拟[29-30]。越野环境下的路径规划,不同的通行对象涉及不同的影响因子,针对轮式车辆为通行对象,本文将影响因子分为地形和地表覆盖类型两种,具体分类见表 1[31-33]。
| 一级分类 | 二级分类 | 描述 |
| 地形 | 坡度 | 地面某点法线与垂线之间的夹角 |
| 高程 | 某点沿铅垂线方向到绝对基准面的距离 | |
| 地表覆盖类型 | 硬质路面 | 高速公路、省道、普通公路等 |
| 土质路面 | 耕地、裸地等可通行的陆地 | |
| 建筑物 | 居民房屋等建筑物 | |
| 草地 | 生长草本和灌木植物等 | |
| 水系 | 江河、湖泊和水库等 | |
| 森林 | 乔木林、竹林等 |
为了建立贴近通行环境的影响因子量化模型,本文将量化规则分为单因子量化和多因子量化。单因子量化得出格网是否能通行,用于筛选出不可通行的格网;在格网可通行的基础上,多因子量化用于计算格网通行能力。
(1) 单影响因子量化。通过确定单一影响因子的格网面积占比或存在与否,判断格网通行性。本文将建筑物和水系进行单影响因子量化,判断规则为
 (1)
(1)
式中, sb和sw为建筑物与水体在对应格网中所占面积;HS代表硬质路面;S为对应格网面积;p为不可通行的影响因子在格网中所占面积比例的阈值。建筑物和水体在格网中所占面积比例之和小于阈值p时,格网可通行;大于等于阈值p,且格网中不存在硬质路面时,格网不可通行。依据实际应用场景和通行对象类型,本文设定p值为0.5。
(2) 多影响因子量化。当格网的通行性为可通行时,对多种影响因子进行综合量化,得到格网通行能力。坡度会影响车辆的通行速度,坡度越大,车辆受到爬坡阻力越大,通行速度越小。量化规则Ws为
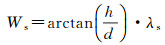 (2)
(2)
式中,h为相邻格网之间的高程差;d为相邻格网之间的中心点距离;λs为坡度对车辆通行速度的影响系数。
硬质路面、土质路面、草地和森林的土质松软程度和地面粗糙程度各不相同,对车辆通行速度也存在着不同的影响。在本文中,它们的量化规则分为两种:①当格网中存在硬质路面时,格网通行能力不受地表覆盖类型影响;②当格网中不存在硬质路面时,使用土质路面、草地和森林在格网中的面积占比与对于车辆速度的影响系数的乘积之和来表示它们对于格网通行能力的影响能力。量化规则Wc为
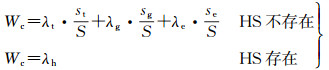 (3)
(3)
式中,S为对应格网面积;HS代表硬质路面;st、sg、se分别为土质路面、草地和森林在对应格网中的面积;λh、λt、λg、λe分别为格网中覆盖类型为硬质路面、土质路面、草地和森林时对车辆速度的影响系数。
综合以上两种量化规则,得出格网n处的通行能力量化模型为
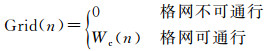 (4)
(4)
式中,Wc(n)为格网n处地表覆盖类型对格网通行能力的影响能力。为了方便使用,还需要对Wc(n)进行归一化操作
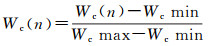 (5)
(5)
式中,Wc min、Wc max为Wc(n)的最小值和最大值。
因此,根据式(4)和式(5),可以得到顾及多种影响因子的格网通行能力量化模型
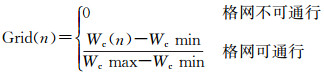 (6)
(6)
多层次通行模型的构建需要经历格网层次压缩与邻接关系重构两个过程。其具体步骤为:①将格网地图中的所有格网作为初始集合S1。②对S1中的格网进行格网层次压缩,将被压缩的格网组成集合S2,再对S2进行邻接关系重构;将S2从S1中删除,生成集合S3。③将S2作为步骤②中的S1,重复步骤②。当S2为空时,将步骤②每次生成的集合S3合并,生成多层次通行模型。
1.2.1 格网层次压缩基于相邻格网层级之间的涵盖关系,本文提出了多层次格网压缩算法,该算法将通行能力相似的邻接子格网合并为父格网。设一组邻接子格网集合C的通行能力为si(i=1, 2, …, n),σ为C中所有格网通行能力的相似度
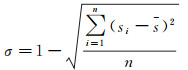 (7)
(7)
当相似度大于或等于格网相似度阈值ρ时,即σ≥ρ,表明集合C中所有格网表达的通行环境相似,可以被压缩为父格网,则压缩后生成的父格网通行能力为W
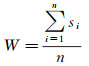 (8)
(8)
在本文所构建的多层次格网剖分系统中,n取值为7,ρ综合对比试验结果及本文应用场景取值为0.80。
1.2.2 邻接关系重构在多层次格网地图中,由于原先格网邻接关系失效,路径规划算法不能够正确运行,因此需要重新构建格网邻接关系。设格网T的子格网为集合A,A的邻接格网为集合U,则格网T的邻接格网集合B={x: x∈U and x∉A},如图 4所示,橙色部分为集合B。再将格网T增添到B中格网的邻接格网集合,邻接关系重构完成。
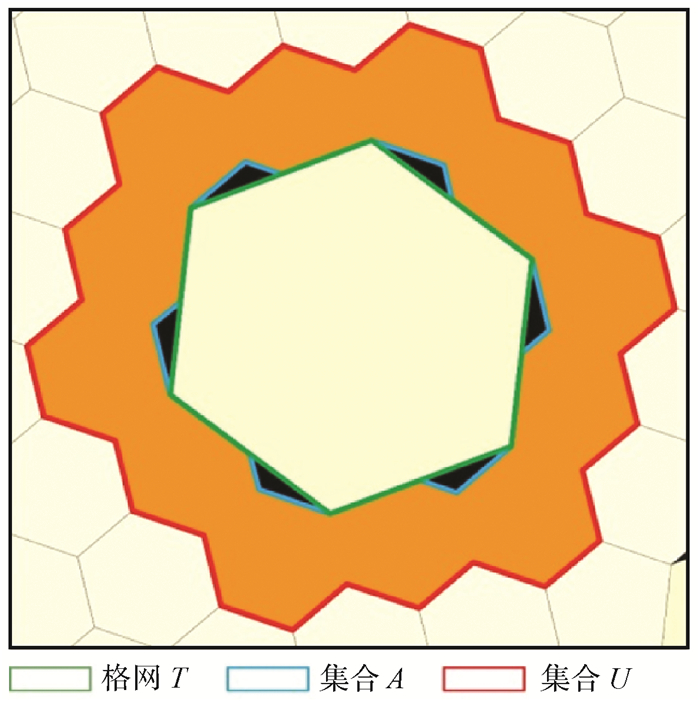
|
| 图 4 邻接关系求解 Fig. 4 Solving adjacency relation |
在多层次格网地图中,不同尺寸格网会出现部分未覆盖或格网重叠的问题,如图 5所示,这些问题会导致地理坐标不能映射到格网或映射格网冲突。为了解决这个问题,基于多层次格网剖分系统地理坐标与格网映射机制,本文在进行地理坐标映射时采取从格网地图最低层级逐级向上转换策略,正确计算地理坐标对应的格网索引,消除格网地图逻辑上空缺与重叠部分。

|
| 图 5 多层次格网地图 Fig. 5 Multi-hierarchy grid map |
如图 6(a)所示,在获取坐标点a所在格网时,虽然格网A与格网B存在叠加关系,但依照最低层级逐级向上转换策略,坐标点a会被定位到格网B;在获取坐标点b所在格网时,会首先得到格网C,而格网C已被压缩为父格网A,所以坐标点b被定位到格网A。实际上,格网A所覆盖的区域为区域B,如图 6(b)所示。
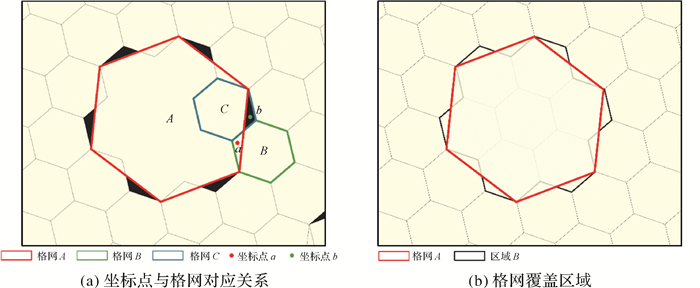
|
| 图 6 多层次格网坐标点与格网对应关系及格网覆盖区域 Fig. 6 Correspondence between coordinates and grid in multi-hierarchies grid maps and grid coverage area |
1.3 路径规划算法
A*算法作为启发式算法,通过对启发函数的设计,可以减少无谓的路径搜索,缩小搜索范围,提高搜索效率[34],其启发函数可以表示为
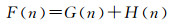 (9)
(9)
式中,F(n)为当前格网n的综合估计值,当需要遍历下一个格网时,算法总会选取综合估计值优先级最高的格网;G(n)为当前格网n距离起始点的实际代价;H(n)为当前格网n距离终点的预估代价。
为了适应多层次格网地图格网大小不一的特点,本文摒弃通过格网数乘以格网大小计算当前格网G(n)的方式,转而采用从起点到当前格网n所经过格网距离之和计算G(n),如式(10)所示
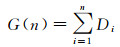 (10)
(10)
式中,Di为从起点格网到当前格网n所经过的第i段路径,如图 7所示。
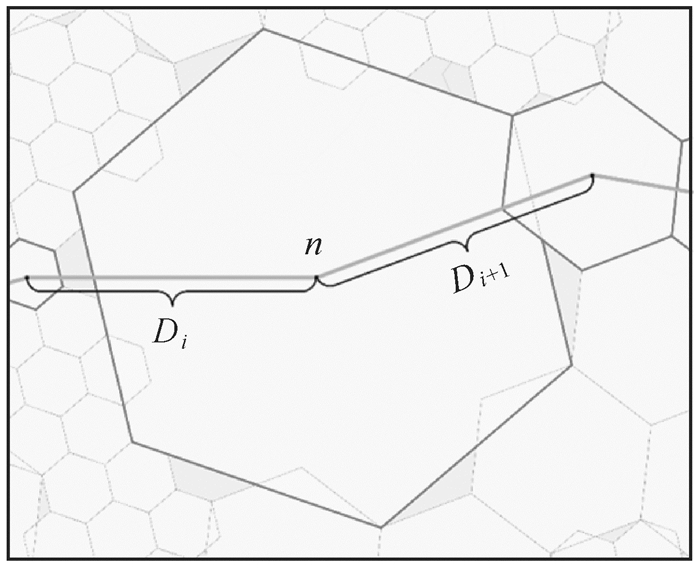
|
| 图 7 G(n)计算 Fig. 7 G(n) calculation |
针对越野环境下的路径规划,本文选取格网通行能力与相邻格网间的坡度值作为启发因素。H(n)为当前格网n到终点格网goal的欧氏距离与启发因素的累加的乘积
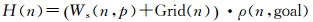 (11)
(11)
式中,Ws(n, p)为n格网处坡度对格网通行能力的影响能力,求解过程中的邻接格网为当前格网n与它的前驱格网p;Grid(n)为当前格网n的通行能力值;ρ(n, goal)为当前格网n到终点格网goal的欧氏距离。
此外,为了保证启发因素量纲统一,且H(n)估计值不能大于当前格网n到终点格网goal的实际值[35],须先对其进行归一化操作
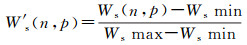 (12)
(12)
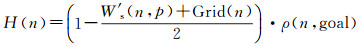 (13)
(13)
综上可得综合两种影响因子的A*算法综合估计值函数
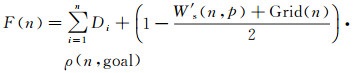 (14)
(14)
本文选取贵州省毕节市黔西县境内部分区域,如图 8所示,该区域中的地表覆盖类型主要为森林与土质路面,四方山峦绵延,中部地势平坦开阔,较适宜作为试验区。其中遥感影像数据为谷歌卫星影像,空间分辨率为0.6 m;数字高程数据为美国国家航空航天局NASA提供的DEM数据, 空间分辨率为30 m;土地利用分类数据为2020年GlobeLand(http://www.globallandcover.com/)全球土地覆盖,空间分辨率为30 m。
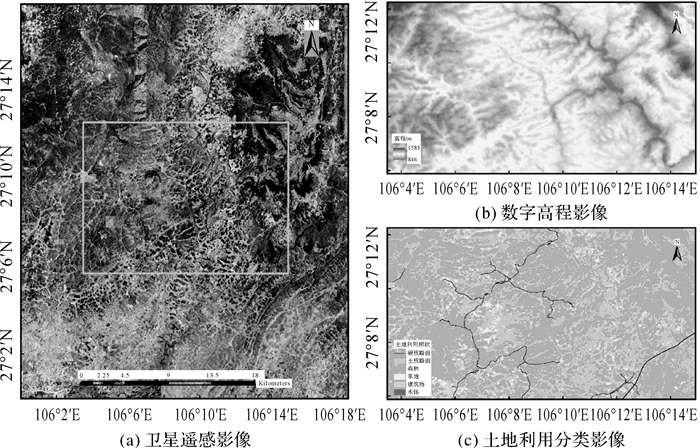
|
| 图 8 试验区区位 Fig. 8 Location of experimental area |
2.2 多层次通行模型结果 2.2.1 影响因子的计算
为了更好地模拟通行环境,建立贴近通行环境的通行模型,基于1.1.2节影响因子量化,本文构建了坡度、硬质路面、土质路面、草地和森林对于车辆速度的影响系数λs、λh、λt、λg、λe,见表 2、表 3。Ws与Wc的取值范围由影响系数确定,由表 3可知,Ws max与Wc max取值为1,Ws min与Wc min取值为0。
| 坡度/(°) | 0 | 3 | 6 | 10 | 15 | 20 | 30 |
| λs | 1.00 | 0.80 | 0.60 | 0.48 | 0.32 | 0.20 | 0 |
| 地表覆盖类型 | 硬质路面(λh) | 土质路面(λt) | 草地(λg) | 森林(λe) |
| λ | 1.0 | 0.9 | 0.6 | 0 |
2.2.2 多层次通行模型的生成
生成多层次通行模型首先需要确定基础格网分辨率,格网分辨率的确定需要综合考虑地图比例尺、研究区域范围大小、应用需求等因素。图 9展示了不同格网分辨率的通行模型,其中线要素为不同等级的公路,在本文中均被表示为硬质路面地表覆盖类型。对比不同格网分辨率的通行模型可以发现,当格网分辨率为R=9时,通行环境可以得到很好的模拟,如图 9(c)所示。以硬质路面为例,在基础格网分辨率采用R=9时,硬质路面经过的格网都表现出了最佳的通行能力。而当基础格网分辨率为R=8、R=7或更低时,格网的表达的通行能力较为粗糙,如图 9(b)右下角所示,格网并没有体现出硬质路面所带来的通行能力提升。在此格网分辨率生成的通行模型中进行路径规划,规划出的路径会出现没有优先经过硬质路面的情况。虽然格网分辨率越大,格网量化精度越高,所表达的通行环境越精细,如图 9(d)所示,硬质路面经过的格网同样表现出了最佳的通行能力;但当格网的分辨率超过地理环境的实际分辨率时,会出现格网量化时没有坐标点相对应的情况。在图 9(d)中,没有坐标点映射的区域存在格网缺失,因此无法进行路径规划研究。综上本文以R=9为基础格网分辨率构建多层次通行模型。

|
| 图 9 不同格网分辨率通行模型对比 Fig. 9 Comparison of traffic models with different grid resolutions |
采用第1.2节多层次通行模型构建方法生成多层次通行模型,如图 10所示。由图 10可以看出,一些通行能力相似的格网都被压缩为了更高层次的格网,通行环境细节也没有丢失。表 4所示为不同参数通行模型格网数量,可以看出以多层次通行模型格网数量仅为R=9的普通通行模型的53.75%。

|
| 图 10 多层次通行模型 Fig. 10 Multi-hierarchy traffic model |
| 通行模型 | 格网数量 |
| R=7 | 46 |
| R=8 | 316 |
| R=9 | 2208 |
| R=10 | 15 453 |
| 多层次 | 1187 |
2.3 通行模型有效性评价
本文使用多层次六角格网通行模型与普通六角格网通行模型进行对比,路径规划算法均为A*算法,启发因素一致,两种通行模型如图 11所示。

|
| 图 11 通行模型对比 Fig. 11 Traffic model comparison |
为了讨论多层次六角格网通行模型对于越野路径规划的影响,以及基于该模型规划路径的合理性,本文选取5组起点O和终点D,并展示了O3D3的路径结果。5组OD均距离较远且地表覆盖复杂,其中O2D2位于海拔较高且坡度多变的多山地带,如图 12所示。

|
| 图 12 越野路径规划结果 Fig. 12 Results of off-road path planning |
对比两条路径可以发现,PN与PO在起点处路径基本一致,说明在没有格网层次压缩的区域,多层次通行模型与普通通行模型规划路径质量相同;中部区域通行环境多变,存在多个格网被压缩的现象,格网邻接关系发生变化,PN与PO在p1处产生了分歧。其中,PN折向右下方,以保证尽量沿着硬质路面前行,有较好的通行环境,但路径不够平滑,拐点较多,对于考虑转弯半径的通行对象,会影响其通行或行进速度;而PO路径笔直,经过的格网通行难度较低且通过格网数少,因此路径平滑且长度较短;最后,靠近终点时,PN与PO所经过的区域通行难度相似,以路径最短前行,说明启发函数中的距离因素有效引导了通行对象的行动。
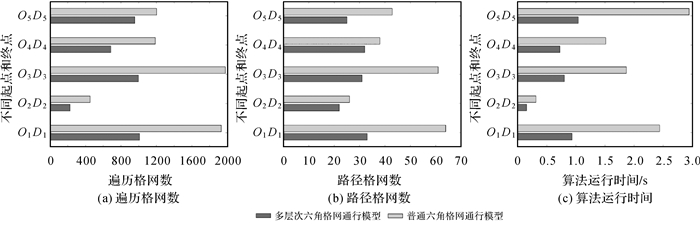
(1) 算法效率对比。本文以遍历格网数、路径格网数、算法执行时间指标对算法效率进行定量分析,其结果如图 13所示。格网层次压缩算法降低了通行模型格网数量的规模,极大地缩小了算法的搜索空间,使得基于多层次六角格网通行模型的路径规划算法相较于普通六角格网通行模型,遍历格网数平均减少了47%。本文提出的路径规划算法在寻找路径的过程中,需要在待遍历格网集合中选择通行能力值最大的格网进行,因此待遍历格网集合越小,路径规划算法的执行效率越高。试验结果表明,基于多层次六角格网通行模型的算法效率较普通通行模型明显提高,其算法执行时间大大降低,平均减少了57%;在路径格网数量上,由于O2D2和O4D4经过的区域格网通行能力的相似度较低,被层次压缩的格网数量较少,所以两种通行模型在路径格网数量上相差不大,但也有16%的数量缩减。
|
| 图 13 算法运行效率对比 Fig. 13 Comparison of algorithm operation efficiency |
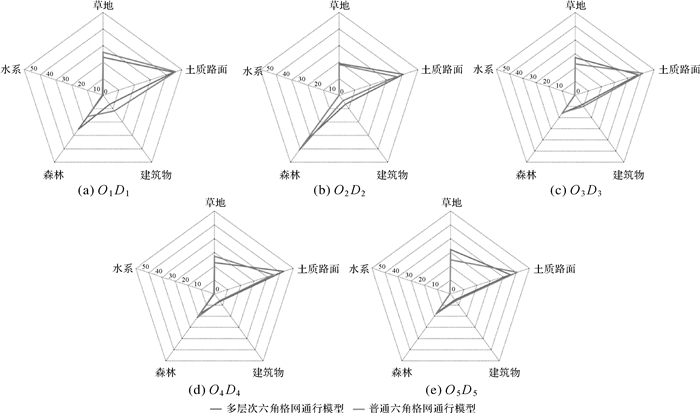
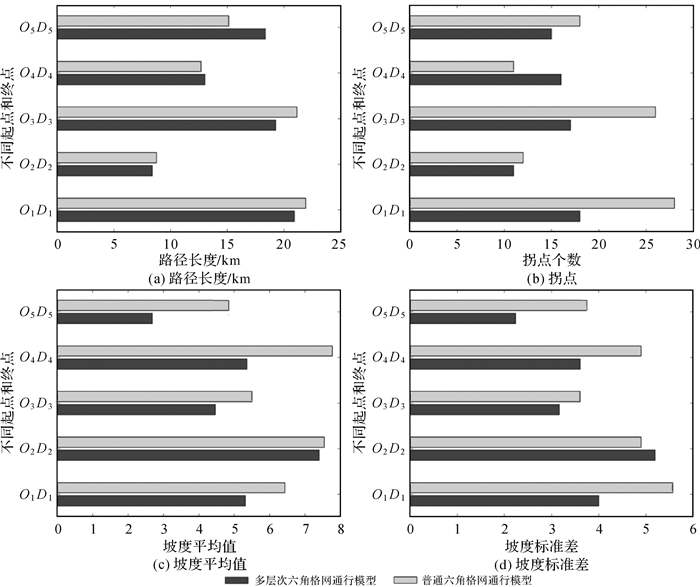
(2) 算法可靠性对比。本文选择路径地表覆盖类型占比、路径长度、拐点、坡度平均值与标准差作为定量指标,使用余弦距离来量化两种通行模型在地表覆盖类型占比分布相似度,综合对比规划路径的优劣。由图 14和图 15可以看出,两种通行模型在通行环境上基本相似,地表覆盖类型占比分布相似度平均值高达98.75%,路径长度平均相差6%,但基于多层次六角格网通行模型的路径坡度的平均值与标准差更小,拐点更少,路径平坦顺滑,更易通行。具体来说,在O3D3中,PN与PO地表覆盖类型占比指标分布相似度为99.5%,PO在路径长度、坡度的平均值和标准差指标上更低,且PO的拐点仅为PN的一半,PO在确保与PN相似路况的前提下,规划了更短、更平坦、更顺滑的路径,充分体现了基于多层次六角格网通行模型规划路径的有效性。另外,虽然O4D4在多层次六角格网通行模型上拐点较多,但路径坡度的平均值与标准差更小,路径更加平坦;O2D2在多层次六角格网通行模型上路径坡度的平均值与标准差较大,但路径拐点更少,路径更加顺滑,通过的格网地表覆盖土质路面更多。由此可以看出,本文提出顾及多种影响因子的越野路径规划算法是可靠的。
|
| 图 14 路径地表覆盖类型占比 Fig. 14 Proportion of path land cover type |
|
| 图 15 算法结果质量对比 Fig. 15 Comparison of quality of algorithm results |
综上,不同于通行环境相对简单的基于路网的路径规划,越野条件下的通行环境复杂,没有道路网约束且规划区域广阔。本文针对这种特点建立了顾及地形与地表覆盖类型两类影响因子的多层次六角格网通行模型,选取遍历格网数、路径格网数及算法执行时间等8个指标衡量多层次六角格网通行模型的优越性。试验结果表明,在通行环境局部相似度高的大规模越野环境中,本文提出的建模方法有效减少了路径规划应用的所需计算时间与存储空间,缩减程度均达到近50%,其规划路径结果也是可以被接受的。
3 总结面对大规模越野环境下路径规划效率低下的问题,本文提出了多层次六角格网通行模型,并基于该模型实现了顾及多影响因子的越野路径规划算法。基于多层次格网剖分系统,普通六角格网通行模型历经相似格网压缩,邻接关系重构,最终生成了多层次六角格网通行模型,并对A*算法启发函数进行优化,使其具有更高的效率与可靠性。试验表明,本文提出的通行模型在大规模越野场景中能保持良好的整体性能,相较于普通六角格网通行模型,有效降低了通行模型的格网数据规模,减少了算法的运行时间。
本文在实现多层次六角格网通行模型时,多层次格网压缩算法仅考虑了格网的通行能力作为压缩标准,压缩后的格网不能完全拟合真实通行环境。因此,后续工作还需在格网相似程度的多因素判断方法上进行探索,进一步优化多层次六角格网通行模型。
| [1] |
王文刚, 张秀丽, 王曦鸣. 基于模糊化环境建模的无人车路径规划研究[J]. 国防制造技术, 2009(3): 53-56. WANG Wengang, ZHANG Xiuli, WANG Ximing. Path planning for unmanned ground vehicle based on fuzzy obstacles environment model[J]. Defense Manufacturing Technology, 2009(3): 53-56. |
| [2] |
KUNDRA H, SOOD M. Cross-country path finding using hybrid approach of PSO and BBO[J]. International Journal of Computer Applications, 2010, 7(6): 15-19. DOI:10.5120/1167-1370 |
| [3] |
王书勤, 黄茜. 军事定向越野路径优化问题建模及混合蚁群算法求解[J]. 运筹与管理, 2018, 27(4): 105-111. WANG Shuqin, HUANG Qian. Route optimization model of military orienteering and its solution to a hybrid ant colony algorithm[J]. Operations Research and Management Science, 2018, 27(4): 105-111. |
| [4] |
陈长林, 孙迈, 宋顺达. 基于扩展Voronoi图的兵力机动路线决策[J]. 指挥控制与仿真, 2010, 32(3): 24-27. CHEN Changlin, SEN Mai, SONG Shunda. Decision-making of forces maneuver path based-on extended Voronoi diagram[J]. Command Control & Simulation, 2010, 32(3): 24-27. |
| [5] |
张欣, 李培宁, 顾明强. 计算机兵棋中越野机动路径网络分析[J]. 地理空间信息, 2017, 15(3): 14-16. ZHANG Xin, LI Peining, GU Mingqiang. Cross-country maneuver path network analysis of the computer wargame[J]. Geospatial Information, 2017, 15(3): 14-16. |
| [6] |
ZHUO Qunlong. Dynamic path planning of mobile robot based on ant colony algorithm[J]. International Journal of Reasoning-based Intelligent Systems, 2018, 10(2): 122-127. DOI:10.1504/IJRIS.2018.092215 |
| [7] |
HUSSEIN A, MARÍN-PLAZA P, MARTÍN D, et al. Autonomous off-road navigation using stereo-vision and laser-rangefinder fusion for outdoor obstacles detection[C]//Proceedings of 2016 IEEE Intelligent Vehicles Symposium (Ⅳ). New York: ACM Press, 2016: 104-109.
|
| [8] |
NEDJATI A, IZBIRAK G, VIZVARI B, et al. Complete coverage path planning for a multi-UAV response system in post-earthquake assessment[J]. Robotics, 2016, 5(4): 26. DOI:10.3390/robotics5040026 |
| [9] |
DENG Lizheng, YUAN Hongyong, HUANG Lida, et al. Post-earthquake search via an autonomous UAV: hybrid algorithm and 3D path planning[C]// Proceedings of the 14th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery. Huangshan: IEEE, 2018: 1329-1334.
|
| [10] |
KUMAR DEBNATH S, OMAR R, ABDUL LATIP N B, et al. A review on graph search algorithms for optimal energy efficient path planning for an unmanned air vehicle[J]. Indonesian Journal of Electrical Engineering and Computer Science, 2019, 15(2): 743-749. DOI:10.11591/ijeecs.v15.i2.pp743-749 |
| [11] |
王艳萍, 刘文堂, 赵宜宾, 等. 多发点情况下地震救援路径的优选算法[J]. 世界地震工程, 2010, 26(1): 121-124. WANG Yanping, LIU Wentang, ZHAO Yibin, et al. Optimization algorithm of earthquake rescue routes for multi-start conditions[J]. World Earthquake Engineering, 2010, 26(1): 121-124. |
| [12] |
孙玉泽. 无人轮式车辆越野路面全局路径规划与轨迹跟踪[D]. 长春: 吉林大学, 2020. SUN Yuze. Global path planning and trajectory tracking of unmanned wheeled vehicles on terrains[D]. Changchun: Jilin University, 2020. |
| [13] |
汪永红, 崔铁军, 吴正升. 嵌入式GIS中最优路径规划算法研究与实现[J]. 测绘科学, 2010, 35(2): 147-149. WANG Yonghong, CUI Tiejun, WU Zhengsheng. Research and implementation of the optimal route planning algorithm in embedded GIS[J]. Science of Surveying and Mapping, 2010, 35(2): 147-149. |
| [14] |
PAPADAKIS P. Terrain traversability analysis methods for unmanned ground vehicles: a survey[J]. Engineering Applications of Artificial Intelligence, 2013, 26(4): 1373-1385. |
| [15] |
蒋键. 智能车辆越野环境路径规划[D]. 北京: 北京理工大学, 2016. JIANG Jian. Path planning of intelligent vehicles on uneven terrain[D]. Beijing: Beijing Institute of Technology, 2016. |
| [16] |
林辉, 彭长辉. 地理信息系统中栅格单元大小和形状的选择[J]. 遥感信息, 2001, 16(1): 21-23. LIN Hui, PENG Changhui. The role of raster pixel size and shape in geographic information system[J]. Remote Sensing Information, 2001, 16(1): 21-23. |
| [17] |
王维才, 艾廷华, 晏雄锋, 等. 多约束条件下的正六边形格网室内路径规划[J]. 武汉大学学报(信息科学版), 2020, 45(1): 111-118. WANG Weicai, AI Tinghua, YAN Xiongfeng, et al. Indoor route planning under regular hexagonal grid considering multi-constraints[J]. Geomatics and Information Science of Wuhan University, 2020, 45(1): 111-118. |
| [18] |
范林林, 华一新. 一种基于六角格的越野通行方法[J]. 测绘通报, 2017(2): 25-29, 59. FAN Linlin, HUA Yixin. A method of cross-country access based on hexagonal grid[J]. Bulletin of Surveying and Mapping, 2017(2): 25-29, 59. |
| [19] |
翁敏, 毋河海, 李林燕. 层次空间推理的机制及其在路径寻找方面的应用[J]. 测绘科学, 2006, 31(5): 119-121. WENG Min, WU Hehai, LI Linyan. Hierarchical spatial reasoning and its application to wayfinding[J]. Science of Surveying and Mapping, 2006, 31(5): 119-121. |
| [20] |
张志然, 刘纪平, 仇阿根, 等. 面向大规模道路网的最短路径近似算法[J]. 测绘学报, 2019, 48(1): 86-94. ZHANG Zhiran, LIU Jiping, QIU Agen, et al. The shortest path approximation algorithm for large scale road network[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(1): 86-94. DOI:10.11947/j.AGCS.2019.20180007 |
| [21] |
汪永红. 多尺度道路网路径规划关键技术及应用研究[D]. 郑州: 信息工程大学, 2011. WANG Yonghong. Study of key technique and application of the optimal route based on multi-scale road network[D]. Zhengzhou: Information Engineering University, 2011. |
| [22] |
DELLING D, SANDERS P, SCHULTES D, et al. Engineering route planning algorithms[M]//Algorithmics of Large and Complex Networks. Berlin: Springer, 2009: 117-139.
|
| [23] |
XU Qing, FENG Shisheng, SUN Qun, et al. A method of planning disaster emergency rescue paths in road-free environment[EB/OL]. [2022-03-01]. http://www.hindawi.com/journals/cin/2022/2987852/.
|
| [24] |
吴天羿, 许继恒, 刘建永, 等. 基于改进A*算法的越野路径规划研究[J]. 计算机应用研究, 2013, 30(6): 1724-1726. WU Tianyi, XU Jiheng, LIU Jianyong, et al. Research of cross-country path planning based on improved A* algorithm[J]. Application Research of Computers, 2013, 30(6): 1724-1726. |
| [25] |
LIU Qinghe, ZHAO Lijun, TAN Zhibin, et al. Global path planning for autonomous vehicles in off-road environment via an A-star algorithm[J]. International Journal of Vehicle Autonomous Systems, 2017, 13(4): 330-339. |
| [26] |
武丽丽, 华一新, 徐青. 基于六角格的陆地边界环境模型构建方法研究[J]. 测绘与空间地理信息, 2013, 36(2): 22-26. WU Lili, HUA Yixin, XU Qing. Study on hexagon-based land boundary environment model[J]. Geomatics & Spatial Information Technology, 2013, 36(2): 22-26. |
| [27] |
周成军, 张锦明, 范嘉宾, 等. 训练模拟系统中地形量化模型的探讨[J]. 测绘科学技术学报, 2010, 27(2): 149-152. ZHOU Chengjun, ZHANG Jinming, FAN Jiabin, et al. Research terrain measured model applied in the training simulation system[J]. Journal of Geomatics Science and Technology, 2010, 27(2): 149-152. |
| [28] |
BRODSKY I. H3: hexagonal hierarchical geospatial indexing system[EB/OL]. [2022-03-01]. http://www.uber.com/blog/h3/.
|
| [29] |
RIEDEL S L, PITZ G F. Utilization-oriented evaluation of decision support systems[J]. IEEE Transactions on Systems, Man and Cybernetics, 1986, 16(6): 980-996. |
| [30] |
MUSIAKA Ł, NALEJ M. Application of GIS tools in the measurement analysis of urban spatial layouts using the square grid method[J]. ISPRS International Journal of Geo-Information, 2021, 10(8): 558. |
| [31] |
范林林. 基于六角格网的越野路径规划技术方法研究[D]. 郑州: 信息工程大学, 2017. FAN Linlin. Research on cross-country path planning technology based on hexagonal grid[D]. Zhengzhou: Information Engineering University, 2017. |
| [32] |
李坤伟, 游雄, 张欣, 等. 基于多源数据的土壤越野通行性评估[J]. 测绘科学技术学报, 2018, 35(2): 206-210. LI Kunwei, YOU Xiong, ZHANG Xin, et al. Evaluation of soil trafficability based on multi-source data[J]. Journal of Geomatics Science and Technology, 2018, 35(2): 206-210. |
| [33] |
RYBANSKY M. Soil trafficability analysis[C]//Proceedings of 2015 International Conference on Military Technologies. Brno: IEEE, 2015: 1-5.
|
| [34] |
HART P, NILSSON N, RAPHAEL B. A formal basis for the heuristic determination of minimum cost paths[J]. IEEE Transactions on Systems Science and Cybernetics, 1968, 4(2): 100-107. |
| [35] |
BOMERS A, SCHIELEN R J, HULSCHER S H. The influence of grid shape and grid size on hydraulic river modelling performance[J]. Environmental Fluid Mechanics, 2019, 19(5): 1273-1294. |



