2. 武汉大学测绘遥感信息工程国家重点实验室, 湖北 武汉 430079;
3. 清华大学计算机系, 北京 100084;
4. 北京跟踪与通信技术研究所, 北京 100094;
5. 91977部队, 北京 100036;
6. 海军航空大学信息融合研究所, 山东 烟台 264000;
7. 北京理工大学前沿技术研究院, 山东 济南 250300
2. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China;
3. Department of Computer Science, Tsinghua University, Beijing 100084, China;
4. Beijing Institute of Tracking and Telecommunications Technology, Beijing 100094, China;
5. Troops 91977, Beijing 100036, China;
6. Institute of Information Fusion, Naval Aviation University, Yantai 264000, China;
7. Institute of Advanced Technology, Beijing Institute of Technology, Jinan 250300, China
舰船运动状态感知对于交通监管、海上救援和战场监视等具有重要意义,是长期的研究热点[1]。相比于无人机平台而言[2],高分辨率光学卫星视频能够对同一地区的连续拍摄获取时序卫星影像,具有持续观测时间长、监视范围广、动态监视能力强和跨境侦察的特点,能够为海面舰船目标运动信息获取提供有力的数据支撑。
目前,光学卫星视频的应用研究主要集中在运动目标状态感知[3-8]、遥感图像超分辨率重建[9-11]、地物三维立体重建[12-14]等方面。基于光学卫星视频的运动目标状态感知研究主要着眼于运动目标的检测和跟踪任务,通过适应性改造已有算法,来提高目标检测跟踪精度和效率,而对于运动目标的几何定位以及测速测向等定量估计方法研究较少。文献[15]针对卫星视频中运动车辆小目标,提出一种基于光流法的交通流参数提取方法并通过目视判别进行验证。文献[16]引入即时定位与地图构建(simultaneous localization and mapping, SLAM)技术并通过珠海一号视频验证海上船只定位、速度和方向精度。文献[17]提出基于道路掩膜、高斯混合模型和数据关联的光学卫星视频多目标检测、跟踪和定位算法并验证定位精度。文献利用改进的视觉背景提取器(video background extractor, ViBE)检测算法、基于匹配搜索的跟踪算法及视频属性信息估算目标速度。以上研究大多从卫星视频的像方直接进行距离换算和目标运动参数的粗略估算,由于光学卫星视频通过敏捷姿态调整进行滑动凝视的方式成像,受卫星平台抖动、姿态控制误差和帧间成像视角差异等因素影响,无控精度较差且帧间存在偏移[19],此时缺少几何模型约束和高精度的验证数据,难以实现目标的高精度定量估计。
此外,卫星遥感视角下的舰船目标具有长宽比大和多尺度特征,且经常存在运动方向与坐标轴相交的情况[20-21]。现有基于对地观测平台的视频运动目标跟踪方法主要集中在抗遮挡[22-24]、抗漂移[25-30]、多目标跟踪[8, 31]等研究,较少关注到目标角度估计对于舰船目标跟踪定位精度的影响,使得传统的正框跟踪方法所形成的包络盒中存在冗余,无法精确贴合船体轮廓。已有的带角度估计的斜框跟踪方法主要分为3类:①以基于孪生网络的掩膜估计(siamese-network for mask estimation, SiamMask)[32]为代表的视频目标分割掩膜方法,该类方法在掩膜的基础上计算包络盒四角坐标得到更贴合的目标位置;②借鉴目标检测中的角度分类标签对深度网络进行训练与预测的方法[33-34];③以基于相似变换的大位移估计(large displacement estimation of similarity transformation, LDES)跟踪器[35]为代表的对数极坐标系特征匹配方法,该类方法一般先在笛卡儿坐标系上估计目标位置,再根据目标位置切片在对数极坐标系上估计角度和尺度。前两类方法能够实现端到端的角度估计,但是需要大量样本进行离线训练,制约了实时处理的应用需求,且角度估计在帧间缺乏关联。第3类方法将跟踪问题看作匹配问题,需要第一帧的角度信息作为参照进行帧间传递和变化量估计,但是能够实现在线训练,且在长时序的角度估计中更具连续性和稳定性。然而,对数极坐标系对于中心点特征较为敏感[36],因此第3类方法角度估计精度依赖于中心点位置估计精度。
综上所述,针对现有方法没有充分利用成像几何参数进行目标物方运动状态的高精度定量估计的问题,本文提出一套基于光学卫星视频的舰船目标运动状态定量估计方法,在视频定向和帧间稳像中引入成像几何模型约束,实现对地目标参数估计。针对传统跟踪方法采用正框坐标输出导致目标定位精度下降的问题,本文重点研究了对数极坐标系特征匹配方法,并针对其对于图像中心点特征敏感的问题,以优秀的正框跟踪方法高效卷积算子跟踪器(efficient convolution operator for tracking, ECO)为基础[37],提出一种顾及旋转和尺度估计的舰船稳健跟踪模块ECO_LDES,嵌入到定量估计方法中提升估计精度。最后通过开展星海同步拍摄试验,利用地面实测真值验证了基于光学卫星视频对海目标高精度几何定位和运动状态估计的有效性。
1 光学卫星视频舰船目标运动状态估计原理本文方法首先利用少量地面控制点精化光学卫星视频首帧影像定向参数;其次以首帧影像为基准,对光学卫星视频进行稳像处理;然后对稳像后视频中海面舰船目标进行自动跟踪,通过顾及旋转和尺度估计的斜框预测方法,获得目标在各帧中的像方坐标;最后利用高精度有理多项式系数(rational polynomial coefficient, RPC)模型计算各帧舰船目标的物方坐标,拟合目标轨迹,解算目标各时刻的经纬度、运动速度和方位角(图 1)。为了验证本文所提出卫星视频目标运动状态高精度估计方法的有效性和可行性,协调调度吉林一号光学视频卫星和海面舰船及船载GPS数据测量设备,采用星海同步观测的方式进行试验验证。

|
| 图 1 本文方法总体流程 Fig. 1 Flowchart of the proposed method |
1.1 光学卫星视频高精度定向
基于星上测量参数直接生成的RPC模型存在对地目标定位的系统误差,本文利用少量控制点对首帧视频影像的RPC模型参数进行精化。本文用于处理的数据为光学卫星视频的传感器校正帧序列产品,该产品每帧均附带RPC模型参数文件[22, 38-39]。RPC模型将地面点大地坐标(纬度L、经度P、高程H)与其对应的像点坐标(列数X、行数Y)用比值多项式关联起来。RPC模型的一般形式为
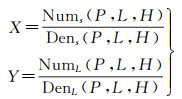 (1)
(1)
式中,(X, Y)为正则化的像点像方坐标;(P, L, H)为正则化的地面点物方坐标;NumS(P, L, H)、DenS(P, L, H)、NumL(P, L, H)、DenL(P, L, H)为三次多项式。
采用仿射变换模型作为RPC模型本身系统误差的补偿模型,通过引入地面控制点数据来修正引起绝对几何定位精度不准的模型误差。系统误差补偿模型定义如下[40]
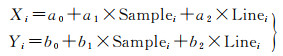 (2)
(2)
式中,(Xi, Yi)为控制点的像点坐标量测值;(Linei, Samplei)为控制点的像点坐标计算值;ai和bi(i=0, 1, 2)是仿射变换系数。最终,通过多个地面控制点计算仿射变换系数并更新RPC参数,实现RPC模型精化。
1.2 光学卫星视频稳像光学视频卫星一般是通过凝视观测的方式成像,在拍摄的过程中因为卫星平台的飞行姿态不稳或者相机抖动等问题,导致各视频帧的外方位元素存在差异,造成背景晃动和影像畸变[41],影响视频的后续处理。因此,视频稳像是视频高精度应用的前提。
视频稳像的主要目的是消除各帧间的相对变形,建立正确的映射关系。经典的视频稳像处理一般由预处理、运动估计、运动补偿3个部分组成。考虑到卫星视频各帧的覆盖范围基本一致,且目前卫星影像的几何处理基本采用RPC模型,光学卫星视频一般采用基于主帧的运动估计和补偿方法进行稳像。本文采用卫星视频稳像方法[41],算法的主要流程如下:
(1) 选取卫星视频的首帧作为主帧,其余帧作为辅帧,利用尺度不变特征变换(scale invariant feature transform, SIFT)算法采用分块模式对主帧和辅帧进行同名点匹配。
(2) 本文以仿射变换模型作为几何约束,采用随机采样一致性(random sample consensus, RANSAC)方法[42]剔除同名点匹配中的粗差。仿射变换模型如式(2)所示。
(3) 基于主帧的卫星视频运动估计,利用匹配获取的同名点计算主帧和辅帧之间的运动估计参数,补偿计算辅帧的RPC模型。
(4) 基于主帧的卫星视频运动补偿,利用步骤(3)求解的辅帧的RPC模型参数,采用双线性内插法将辅帧向主帧进行影像重采样,完成视频运动补偿。
1.3 顾及旋转和尺度变化的海面舰船稳健跟踪相比于普通视频中的运动目标,光学卫星视频地面运动目标一般具有尺寸小、特征少、背景复杂、时敏性强等特点[19],需要选择特殊的目标跟踪方法进行针对性处理,同时还需顾及算法的时效性。本文选择基于相关滤波器的目标跟踪方法,通过快速傅里叶变换(fast Fourier transform, FFT)将图像特征从空间域转换到频率域,大幅度提升了运算效率。其中,ECO跟踪方法[37]是相关滤波类算法中的优秀代表,它在保留连续卷积算子跟踪器(continuous convolutional operators for tracking, CCOT)方法[43]对于多分辨率特征融合和亚像素定位的优势的同时,有效克服了其特征冗余、过拟合和模型漂移等问题,具有较高的算法效率和较强的稳健性,适用于光学卫星视频的弱小目标准确跟踪和实时处理。
ECO方法由相关滤波器和高效卷积算子组成,其实现形式可分为基于卷积特征(传统ECO方法)和基于方向梯度直方图[44]-多通道颜色[45]组合人工特征(ECO based on histogram of oriented gradient and color names, ECO_HC)这两种。考虑到光学卫星视频地面运动目标的特点和算法处理的时效性要求,本文选用ECO_HC方法对地面运动目标进行自动跟踪。
此外,卫星遥感视角下的舰船目标具有长宽比大和多尺度特征,且经常存在运动方向与图像像方坐标轴相交的情况[20-21],使得传统的正框跟踪方法所形成的包络盒中存在信息冗余,检测框无法精确贴合船体轮廓。针对这一问题,本文在ECO_HC的基础上,提出一种顾及旋转和尺度变化的海面舰船快速稳健跟踪方法ECO_LDES,减少跟踪框在长时序数据处理中漂移情况,提升舰船目标定位精度。
1.3.1 相关滤波器相关滤波器跟踪方法主要包含目标位置预测和滤波器更新两个步骤。
假定输入图像为f,选用的滤波器为h,则两者的相似性可利用互相关函数g表示为
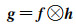 (3)
(3)
f与h相关响应越高的区域,g的值越大,则当g取最大值时,f即为跟踪目标图像。对式(3)进行FFT可得
 (4)
(4)
式中,G、F、H为上述g、f、h的FFT形式。用i表示样本编号,则滤波器h的更新公式为
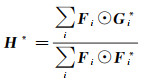 (5)
(5)
对式(5)进行快速傅里叶逆变换(inverse fast Fourier transform, IFFT),即可求解出滤波器h,实现样本与目标的整体偏差最小约束下相关滤波器的更新。
1.3.2 高效卷积算子CCOT方法通过连续空间域插值转换操作,将提取出的特征矩阵转换到连续的空间域,获得融合的特征图(式(6))
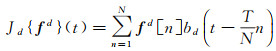 (6)
(6)
式中,Jd{ fd}(t)是建立在希尔伯特空间L2(T)上插值函数bd的累积;t和T分别为连续域变量和连续域支撑空间长度。
ECO方法在此基础上提出了一种卷积的因式分解方法,即高效卷积算子,通过衡量特征矩阵中不同向量的贡献度,剔除贡献极小部分的向量,提取特征子集以实现特征矩阵的降维,从而有效减少模型参数和计算量,充分利用特征信息。
高效卷积算子的计算步骤可归纳为:对于输入样本图像fi,提取D种特征,分别记作fi1, fi2, …, fiD。若这D种特征所对应的特征图具有N种分辨率,且以d∈(0, D]标记其中某一特征,n∈(0, N ]标记其分辨率,那么该特征i可记作函数fid[n]。在每种特征d上,可以用函数Jd来整合不同分辨率的特征图,将其从离散空间映射到连续空间。
如果特征d上的滤波器为h,则其相关性响应为
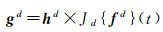 (7)
(7)
对于样本fi上所有D个特征有连续响应函数为
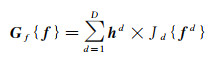 (8)
(8)
由于D个特征在实际应用中对于样本图像中目标跟踪的贡献度各不相同,假设其中的C(C < D)个特征对图像的表达起到了决定性作用。定义一个维度为D×C的矩阵P,那么特征图Jd{ fd}可降维为
 (9)
(9)
高效卷积算子实现了将由HOG特征与CN特征融合得到的42维特征矩阵降至13维的操作,有效降低了算法的复杂度。
此外,ECO跟踪方法采用了高斯混合模型(Guassian mixture model, GMM)将每一帧采集的样本划分到不同的类别,每一个类别基本对应了一组比较相似的样本,不同类别之间的样本具有较大的差异,使整个样本空间更加紧凑并保持样本间的差异性,减少过拟合现象。该方法还通过稀疏的更新策略来实现平稳和快速的目标跟踪。
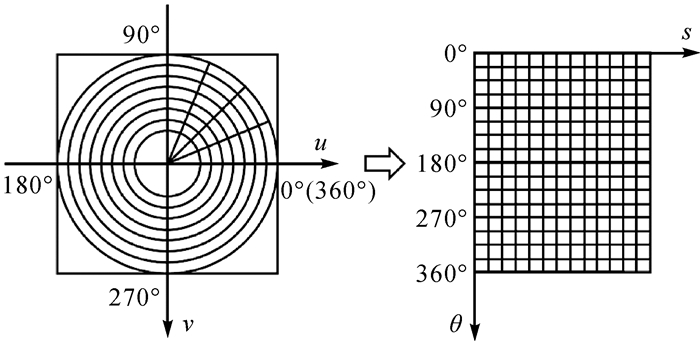
1.3.3 角度和尺度变化量估计由于对数极坐标系的横纵坐标能够分别表示笛卡儿坐标系上目标各像素所在的尺度和角度,当相邻两帧目标的变换中心在笛卡儿坐标系的原点时,求取同名点在对数极坐标系上的平移量即可获得尺度和角度变化量,从而实现目标的斜框跟踪[36]。图 2为对数极坐标变换。
|
| 图 2 对数极坐标变换 Fig. 2 Log-polar transformation |
假设笛卡儿坐标系定义为
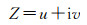 (10)
(10)
式中,Z表示复平面上的一个复数;i表示复数的虚单位;u和v分别表示笛卡儿坐标系的横坐标和纵坐标。以中心点(u0, v0)为原点,与笛卡尔坐标系任意一点坐标(u, v)对应的对数极坐标系下坐标则可表示为(s, θ),s和θ分别表示极径和极角,计算公式为
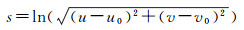 (11)
(11)
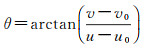 (12)
(12)
若将图像I以原点(u0, v0)旋转Δθ,尺度变化Δs,则变化后的图像在对数极坐标系下可表示为
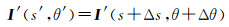 (13)
(13)
基于上述性质,可以在对数极坐标系下通过相关滤波估计出被跟踪目标的旋转和尺度变化量[36]。假设fiP表示训练样本f在对数极坐标系下的特征图,则对数极坐标系下傅里叶域上的第l∈{1, 2, …, d}层滤波器表示为
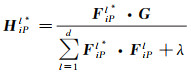 (14)
(14)
式中,FiPl表示fiP的离散傅里叶变换;FiPl*表示FiPl的复共轭;G表示期望输出值g的离散傅里叶变换;λ≥0为正则化参数。
当获得各层滤波器HiPl*后,在目标位置估计阶段,当前帧候选区域xiPl在转换到对数极坐标系下的得分图可表示为
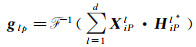 (15)
(15)
式中,XiPl表示xiPl的离散傅里叶变换;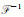
海面舰船目标定位主要利用RPC模型的反算形式,求解在光学卫星视频像方跟踪得到的舰船目标所对应的物方坐标。RPC模型的反算形式为
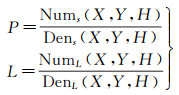 (16)
(16)
当舰船目标在海上航行时,其高程值赋为0。目标点的物方空间平面坐标可通过成像光线与0高程面的交点获取。
为了精准估算出海面运动舰船的瞬时速度和方位角,本文采用第一类切比雪夫多项式模型,对海面舰船目标轨迹的物方坐标进行拟合,并通过拟合参数估计出目标各时刻的速度与方位角。相比于常用的拉格朗日多项式和内维尔插值等拟合方法,切比雪夫多项式拟合弧段较为光滑,不易受异常观测值的影响,适用于较长轨迹的高精度拟合。
以X坐标分量为例,设k为观测个数,Xk为观测值,Ti和i分别为切比雪夫多项式及其阶数,τk为定义在区间[-1, 1]的归一化时间间隔,则误差方程为
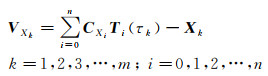 (17)
(17)
通过最小二乘法可求解切比雪夫多项式的拟合系数CXi。同理,可计算出地面运动目标的Y、Z在[t0, t0+Δt]时间内的切比雪夫多项式拟合系数CYi、CZi,从而利用这些系数计算出[t0, t0+Δt]时间内任意时刻的地面运动目标坐标。
利用切比雪夫多项式拟合系数构建轨迹模型,对时间t进行一阶偏导,即可获得该运动目标的速度模型,解算出t0时刻的目标速度;利用t0时刻的目标速度分量vY和vX,可解算对应时刻的瞬时切线方向角θ
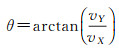 (18)
(18)
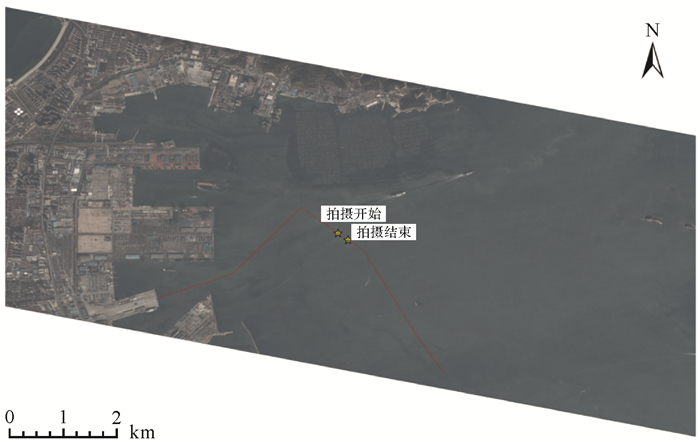
本文试验区位于中国山东省烟台市芝罘湾地区(图 3)。试验采集了一艘试验船在一段时间内的物方经纬度坐标。试验船的物方坐标通过实时服务精密单点定位(real-time service precise point positioning, RTS-PPP)的测量方式得到,测量设备每7 s采集一次测量值,其测量精度能够保证平面和高程方向均优于0.1 m,可用于精度验证(图 4)。与此同时,吉林一号卫星同步拍摄目标航行区域,完成星海同步观测试验。试验的具体参数详见表 1。
|
| 注:红线为试验船航线,黄标为试验船在拍摄开始和结束时的大致位置。 图 3 试验区 Fig. 3 The test area |

|
| 图 4 试验装备 Fig. 4 The test equipments |
| 属性 | 参数 |
| 拍摄地点 | 中国山东省烟台市芝罘湾中部 |
| 拍摄时间 | 2020-10-17 09:45:59至9:46:58 |
| 分辨率/m | 1 |
| 幅宽/km | 11×4.6 |
| 视频尺寸/像素 | 12 000×5000 |
| 拍摄时长/s | 59 |
| 帧率/fps | 10 |
| 数据来源 | 吉林一号视频星03星 |
| 船只名称 | 烟台拖22 |
| 船舶吨位/t | 443 |
| 船长/m | 39.035 |
| 船宽/m | 10.4 |
| 船深/m | 4.7 |
| 吃水深度/m | 3.1 |
| 最大航速/kn | 13.5 |
| 主机功率/kW | 3676 |
2.2 试验结果与分析 2.2.1 光学卫星视频高精度定向试验
本文采集了芝罘湾沿岸地面特征点及试验船坐标(201号点),用于影像定向和精度验证,特征点的空间分布及实地测量情况分别如图 5和图 6所示。

|
| 图 5 试验区地面特征点的空间分布情况 Fig. 5 Spatial distribution of ground feature points in the test area |

|
| 图 6 试验区地面特征点的实地测量(以检查点104为例) Fig. 6 Field measurement of ground feature points in the test area (Take the check point No. 104 for example) |
将所有外业测量点作为检查点,得到试验区首帧影像的无控定位精度(表 2、图 7)。由表 2可知,试验区检查点在平面的像方中误差为524.624像素,说明影像的无控定位精度较低,且图 7中的误差分布具有明显的系统性,可利用少量控制点通过仿射变换对RPC模型进行误差补偿。
| 编号 | 像方X测量值/像素 | 像方Y测量值/像素 | 像方X计算值/像素 | 像方Y计算值/像素 | 残差/像素 | ||
| X方向 | Y方向 | 平面 | |||||
| 101 | 6 456.622 | 98.053 | 6 963.992 | 167.980 | -507.370 | -69.927 | 512.166 |
| 102 | 1 879.518 | 383.889 | 2 409.961 | 443.900 | -530.443 | -60.011 | 533.827 |
| 103 | 2 290.370 | 827.681 | 2 818.368 | 885.177 | -527.998 | -57.496 | 531.119 |
| 104 | 1 985.295 | 2 007.655 | 2 512.774 | 2 058.735 | -527.479 | -51.080 | 529.946 |
| 105 | 4 332.301 | 247.320 | 4 850.557 | 311.700 | -518.256 | -64.380 | 522.239 |
| 106 | 1 241.728 | 2 776.199 | 1 772.495 | 2 821.054 | -530.767 | -44.855 | 532.659 |
| 107 | 2 001.738 | 4 653.035 | 2 528.625 | 4 690.479 | -526.887 | -37.444 | 528.216 |
| 108 | 3 478.119 | 4 204.333 | 3 996.473 | 4 248.669 | -518.354 | -44.336 | 520.247 |
| 201 | 5 939.598 | 2 678.275 | 6 447.041 | 2 735.069 | -507.443 | -56.794 | 510.611 |
| 像方中误差/像素 | 521.740 | 54.930 | 524.624 | ||||
| 像方最大误差/像素 | 530.767 | 69.927 | 533.827 | ||||
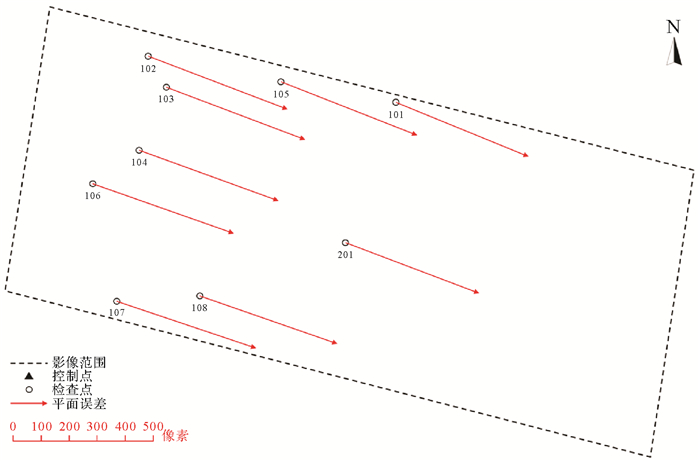
|
| 图 7 无控条件下试验区首帧影像的平面误差分布情况 Fig. 7 Plane errors of the first frame in the test area without ground control points |
选取若干个特征点作为地面控制点,用于求解仿射变换误差补偿模型中的参数,并将其余特征点作为检查点进行精度验证。控制点选取尽可能保证四角布控原则,本文选取101、102、106、108这4个特征点作为控制点(图 8),得到四控条件下试验区首帧影像的定位精度(表 3)。由表 3可知,检查点平面像方中误差为0.980像素,优于1像素,即物方中误差为1 m,且由图 8可见检查点的平面误差分布不具有系统性,说明定向后首帧影像的几何系统误差已经明显消除,能够满足高精度对地目标定位的需要。

|
| 图 8 四控条件下试验区首帧影像的平面误差分布情况 Fig. 8 Plane errors of the first frame in the test area with four ground control points |
| 编号 | 像方X测量值/像素 | 像方Y测量值/像素 | 像方X计算值/像素 | 像方Y计算值/像素 | 残差/像素 | ||
| X方向 | Y方向 | 平面 | |||||
| 103 | 2 818.102 | 885.530 | 2 818.368 | 885.177 | -0.266 | 0.353 | 0.442 |
| 104 | 2 513.338 | 20 59.015 | 2 512.774 | 2 058.735 | 0.564 | 0.280 | 0.630 |
| 105 | 4 850.326 | 312.383 | 4 850.557 | 311.700 | -0.231 | 0.683 | 0.721 |
| 107 | 2 526.943 | 4 691.339 | 2 528.625 | 4 690.479 | -1.682 | 0.860 | 1.889 |
| 201 | 6 446.972 | 2 734.724 | 6 447.041 | 2 735.069 | -0.069 | -0.345 | 0.352 |
| 像方中误差/像素 | 0.810 | 0.553 | 0.980 | ||||
| 像方最大误差/像素 | 1.682 | 0.860 | 1.889 | ||||
2.2.2 光学卫星视频稳像试验
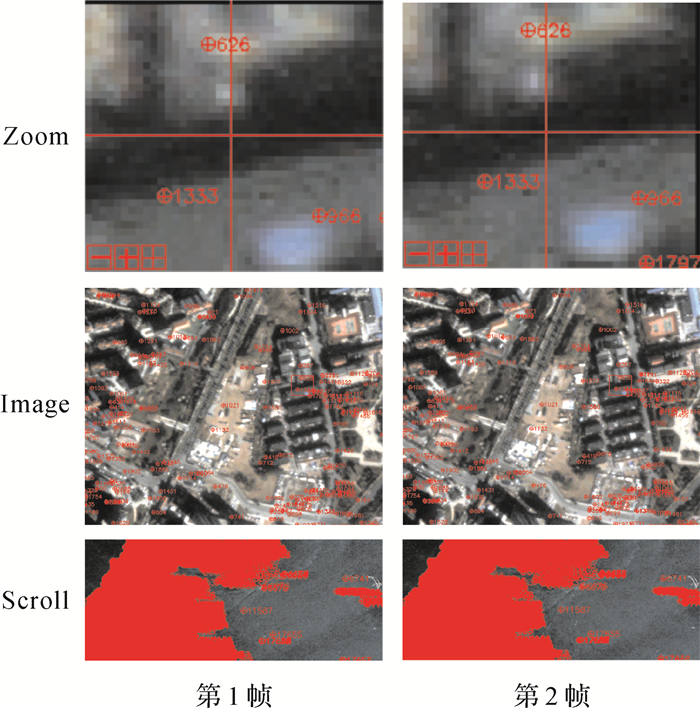
以定向后的首帧影像为主帧,其余帧作为辅帧,利用SIFT方法提取主帧与辅帧的同名点(图 9)。如图 9所示,匹配得到的同名点数量密集且均匀分布在陆地和岛屿上。
|
| 图 9 试验区主辅帧同名点提取情况 Fig. 9 Extraction of homonymy points between prime frame and auxiliary frame in the test area |
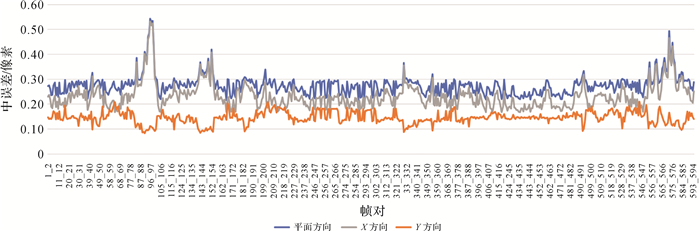
利用提取的同名点计算帧间的仿射变换参数,完成辅帧相对于主帧的运动估计。然后将仿射参数用于更新RPC模型,并对辅帧重采样,完成辅帧相对于主帧的运动补偿,实现卫星视频的帧间稳像。稳像后各帧间同名点的像方中误差如图 10和表 4所示。由图 10和表 4可知,整个视频帧序列(共594帧)的平面方向中误差集中在0.3像素的附近,X方向、Y方向和平面方向的中误差平均值分别为0.23、0.15和0.28像素,能够实现高精度光学卫星视频稳像。
|
| 图 10 试验区各视频帧间在X方向、Y方向、平面方向上的中误差 Fig. 10 RMSE between video frames in X direction, Y direction and plane direction in the test area |
| 帧对 | X方向中误差/像素 | Y方向中误差/像素 | 平面中误差/像素 |
| 1_2 | 0.23 | 0.15 | 0.27 |
| 2_3 | 0.24 | 0.14 | 0.27 |
| 3_4 | 0.22 | 0.14 | 0.26 |
| 4_5 | 0.19 | 0.14 | 0.24 |
| 5_7 | 0.18 | 0.15 | 0.24 |
| 7_8 | 0.22 | 0.17 | 0.28 |
| 8_9 | 0.24 | 0.17 | 0.29 |
| 9_10 | 0.19 | 0.14 | 0.23 |
| ⋮ | ⋮ | ⋮ | ⋮ |
| 584_585 | 0.31 | 0.10 | 0.33 |
| 585_586 | 0.27 | 0.12 | 0.29 |
| 586_587 | 0.27 | 0.12 | 0.29 |
| 587_588 | 0.26 | 0.13 | 0.29 |
| 588_589 | 0.24 | 0.17 | 0.29 |
| 589_590 | 0.27 | 0.13 | 0.30 |
| 590_591 | 0.24 | 0.17 | 0.29 |
| 591_592 | 0.21 | 0.15 | 0.26 |
| 592_593 | 0.21 | 0.16 | 0.27 |
| 平均值 | 0.23 | 0.15 | 0.28 |
2.2.3 舰船目标跟踪试验
为了验证本文所提出的融合角度和尺度变化的相关滤波跟踪方法ECO_LDES对于定位精度提升的有效性,选取目前10种基于正框的单目标跟踪经典方法核相关滤波法(kernelized correlation filters, KCF)[46]、带核方法的循环矩阵法(circulant structure with kernels, CSK)[47]、CCOT[43]、ECO_HC[37]、ECO[37]、时空正则相关滤波器(spatial-temporal regularized correlation filters, STRCF)[48]、基于HoG和CN特征的时空正则相关滤波器(STRCF based on HoG and CN, STRCF_HC)[48]、背景感知相关滤波器(background-aware correlation filters, BACF)[49]、基于HoG和CN特征的自适应判别特征学习相关滤波器(learning adaptive discriminative correlation filters for tracking based on HoG and CN, LADCF_HC)[50]、模板-像素联合学习器(sum of template and pixel-wise learners, STAPLE)[51]和2种基于斜框的单目标跟踪优秀方法(LDES[35]和SiamMask[32]),通过SatSOT开源数据集(包含5段舰船目标跟踪视频)[52]和星海同步拍摄数据ship_YT1进行验证,采用一次性评估法(one-pass evaluation, OPE[53-54])进行精度评价,其中评价指标包括跟踪精确率(即跟踪框和真值框中心点位置之间的欧氏距离阈值小于4像素的帧数所占比例)和跟踪成功率(即跟踪框和真值框之间的交并比曲线下面积)。
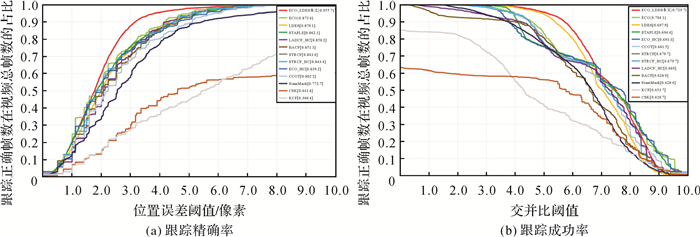
图 11为跟踪算法的定量结果对比情况,其中本文方法ECO_LDES的处理精度最高,在4像素阈值下的跟踪精确率为95.57%,跟踪成功率为72.97%,比原有的正框方法ECO分别提升了8.31%和2.56%,比原有的斜框方法LDES提升了8.56%和3.18%,提升效果显著。
|
| 图 11 各跟踪算法的定量结果对比情况 Fig. 11 Comparison of quantitative results of each tracking algorithm |
图 12为定性结果对比情况。由图 12可知,本文方法ECO_LDES通过旋转和尺度估计生成的斜框,能够更加贴合长宽比较大,与图像像方坐标轴相交的倾斜舰船目标轮廓,相比原来的正框方法ECO提升了定位精度。对数-极坐标变换能估计出目标帧间的旋转与尺度变化量,但其估计精度依赖于目标位置的估计精度,因此将具有多分辨率特征融合和亚像素定位的ECO用于目标的初始位置估计,相比斜框方法LDES在长时序数据处理中具有更高的精度和稳健性(图 13)。本文方法ECO_LDES的定位估计中误差为1.95像素,相比于ECO(3.77像素)和LDES(2.94像素),在定位精度方面也具有最优的效果。

|
| 图 12 各跟踪方法的定性结果对比 Fig. 12 Comparison of qualitative results of each tracking method |

|
| 图 13 正框方法、斜框方法和本文方法在长时序数据上的定位估计精度 Fig. 13 Comparison of the positioning estimation accuracy of the rectangular box method, the rotating box method and the method in this paper on long time series data |
2.2.4 舰船目标定位及运动状态估计试验
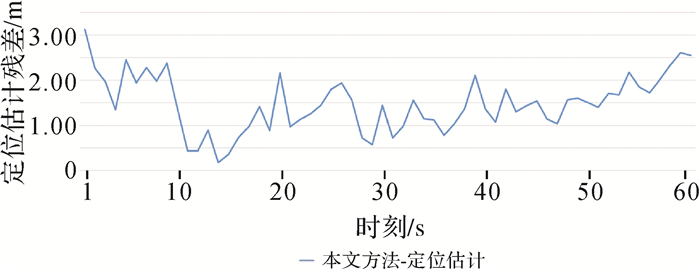
通过本文方法有效实现舰船目标跟踪定位,目标的计算轨迹与真实轨迹的分布情况如图 14所示。图 15为试验船目标在各时刻的定位误差。经计算得知,试验船目标各时刻定位误差的中误差为1.60 m,优于2 m,说明本文所采用的目标跟踪定位方法精度较高;由图 15可知,定位误差控制能够控制在3 m以内,说明本文基于旋转框跟踪的目标定位方法在较长时序视频帧(约600帧)的目标定位中兼具高精度和稳定性。

|
| 图 14 试验船目标计算轨迹(圆圈点)与真值轨迹(三角形)的分布 Fig. 14 The distribution of the calculated value (marked by dots) and the true value (marked by triangles) of the target trajectory |
|
| 图 15 试验船目标在各时刻的定位误差 Fig. 15 The positioning error of the target at each time |
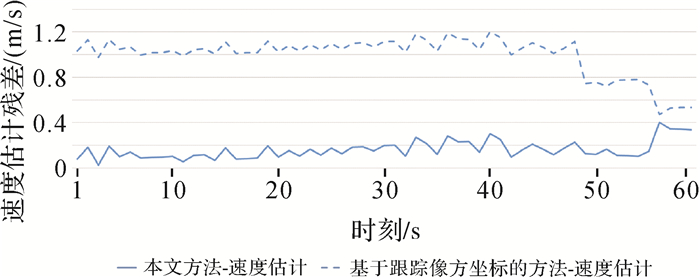
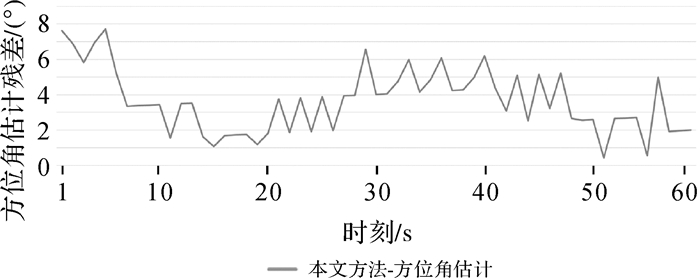
基于目标物方坐标构建轨迹模型,得到目标各时刻的速度和以正北方向为基准的方位角估计值。本文对比了基于像方的目标运动速度估计方法[18],该方法主要利用目标的像方移动距离、影像空间分辨率和帧序列的时间间隔进行估计。图 16和图 17分别为试验船目标各时刻的速度和方位角估计误差,其统计情况见表 5、表 6。由图 16和表 5可知,60 s时间内进行目标速度和方位角精度统计,相比于基于跟踪像方坐标方法的速度估计中误差1.01 m/s,本文方法的速度估计的中误差分别为0.18 m/s。试验结果表明,本文速度估计方法精度提高了一个量级,可以实现精准测速。由图 17和表 6可知,在方位角计算方面,目标方位角中误差达到4.05°,可以实现目标精准测向。
|
| 图 16 试验船目标各时刻速度估计残差 Fig. 16 Residuals of velocity estimation of the test ship target at each time |
|
| 图 17 试验船目标各时刻方位角估计残差 Fig. 17 Residuals of azimuth estimation of the test ship target at each time |
| 时刻 | 真值 | 本文方法 | 基于跟踪像方坐标的方法 | |||
| 估计值 | 残差 | 估计值 | 残差 | |||
| 9:46:00 | 3.90 | 3.82 | 0.08 | 2.87 | 1.03 | |
| 9:46:01 | 4.00 | 3.82 | 0.18 | 2.87 | 1.13 | |
| 9:46:02 | 3.84 | 3.81 | 0.03 | 2.86 | 0.98 | |
| 9:46:03 | 4.00 | 3.81 | 0.19 | 2.86 | 1.14 | |
| 9:46:04 | 3.90 | 3.80 | 0.10 | 2.85 | 1.05 | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| 9:46:54 | 3.42 | 3.56 | 0.15 | 2.69 | 0.73 | |
| 9:46:55 | 3.16 | 3.56 | 0.40 | 2.69 | 0.47 | |
| 9:46:56 | 3.21 | 3.55 | 0.35 | 2.68 | 0.53 | |
| 9:46:57 | 3.21 | 3.55 | 0.34 | 2.67 | 0.53 | |
| 9:46:58 | 3.21 | 3.55 | 0.34 | 2.67 | 0.53 | |
| 速度估计中误差 | 0.18 | 1.01 | ||||
| 时刻 | 真值 | 本文方法 | |
| 估计值 | 残差 | ||
| 9:46:00 | 117.78 | 110.17 | 7.62 |
| 9:46:01 | 117.04 | 110.14 | 6.90 |
| 9:46:02 | 115.94 | 110.11 | 5.82 |
| 9:46:03 | 117.04 | 110.08 | 6.96 |
| 9:46:04 | 117.78 | 110.06 | 7.73 |
| ⋮ | ⋮ | ⋮ | ⋮ |
| 9:46:54 | 109.12 | 108.55 | 0.56 |
| 9:46:55 | 113.50 | 108.52 | 4.98 |
| 9:46:56 | 110.42 | 108.49 | 1.93 |
| 9:46:57 | 110.42 | 108.46 | 1.96 |
| 9:46:58 | 110.42 | 108.42 | 2.00 |
| 方位角估计中误差 | 4.05 | ||
3 结论
利用本文提出的一种基于光学卫星视频的舰船目标运动状态高精度定量估计方法,并通过星海同步观测试验验证,结论如下:
(1) 本文设计的技术流程具有可行性和有效性,能够实现光学卫星视频影像平面精度优于1像素,且稳像精度优于0.3像素,舰船目标几何定位精度优于2 m。
(2) 本文所提出的顾及旋转和尺度变化的海面舰船稳健跟踪方法ECO_LDES能够提升舰船目标的定位精度。在长时序视频处理中的定位精度提升到1.95像素。
(3) 通过星地同步观测试验验证,本文方法实现高精度目标运动状态估计,速度估计精度0.18 m/s,航向估计精度为4.05°。
目前,本文方法仅针对单个卫星视频进行单个目标的运动参数估计,在未来多星组网、协同观测的条件下,多目标的复杂运动状态参数估计将会成为研究重点。本文方法依赖地面控制点,对于远离港口的远海舰船目标定位可以通过船舶自动识别系统(automatic identification system, AIS)数据和岛屿控制点来提升物方精度。此外,如何进一步摆脱对地面控制的依赖是未来值得关注的研究方向之一。
| [1] |
王彦情, 马雷, 田原. 光学遥感图像舰船目标检测与识别综述[J]. 自动化学报, 2011, 37(9): 1029-1039. WANG Yanqing, MA Lei, TIAN Yuan. State-of-the-art of ship detection and recognition in optical remotely sensed imagery[J]. Acta Automatica Sinica, 2011, 37(9): 1029-1039. |
| [2] |
HAN Yuqi, LIU Huaping, WANG Yufeng, et al. A comprehensive review for typical applications based upon unmanned aerial vehicle platform[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2022, 15: 9654-9666. DOI:10.1109/JSTARS.2022.3216564 |
| [3] |
吴佳奇, 张过, 汪韬阳, 等. 结合运动平滑约束与灰度特征的卫星视频点目标跟踪[J]. 测绘学报, 2017, 46(9): 1135-1146. WU Jiaqi, ZHANG Guo, WANG Taoyang, et al. Satellite video point-target tracking in combination with motion smoothness constraint and grayscale feature[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(9): 1135-1146. DOI:10.11947/j.AGCS.2017.20160599 |
| [4] |
ZHANG Junpeng, JIA Xiuping, HU Jiankun. Error bounded foreground and background modeling for moving object detection in satellite videos[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 58(4): 2659-2669. |
| [5] |
ZHANG Junpeng, JIA Xiuping, HU Jiankun, et al. Online structured sparsity-based moving-object detection from satellite videos[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(9): 6420-6433. DOI:10.1109/TGRS.2020.2976855 |
| [6] |
WANG Yunming, WANG Taoyang, ZHANG Guo, et al. Small target tracking in satellite videos using background compensation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(10): 7010-7021. DOI:10.1109/TGRS.2020.2978512 |
| [7] |
SHAO Jia, DU Bo, WU Chen, et al. HRSiam: high-resolution siamese network, towards space-borne satellite video tracking[J]. IEEE Transactions on Image Processing, 2021, 30: 3056-3068. DOI:10.1109/TIP.2020.3045634 |
| [8] |
FENG Jie, ZENG Dening, JIA Xiuping, et al. Cross-frame keypoint-based and spatial motion information-guided networks for moving vehicle detection and tracking in satellite videos[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2021, 177: 116-130. DOI:10.1016/j.isprsjprs.2021.05.005 |
| [9] |
卜丽静, 郑新杰, 张正鹏. 顾及运动估计误差的"凝视"卫星视频运动场景超分辨率重建[J]. 测绘学报, 2020, 49(2): 214-224. BU Lijing, ZHENG Xinjie, ZHANG Zhengpeng. Super-resolution reconstruction of "straring" satellite video motion scene considering motion estimation error[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(2): 214-224. DOI:10.11947/j.AGCS.2020.20180544 |
| [10] |
姚烨. 高分辨率视频卫星影像超分辨率重建技术研究[D]. 长春: 中国科学院大学(中国科学院长春光学精密机械与物理研究所), 2018. YAO Ye. Research on super-resolution reconstruction of high resolution video satellite images[D]. Changchun: University of Chinese Academy of Sciences(Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences), 2018. |
| [11] |
XIE Qifang, YAO Guoqing, LIU Pin. Super-resolution reconstruction of satellite video images based on interpolation method[J]. Procedia Computer Science, 2017, 107: 454-459. DOI:10.1016/j.procs.2017.03.089 |
| [12] |
范江. 基于视频卫星影像的DSM生成技术研究[D]. 武汉: 华中科技大学, 2019. FAN Jiang. Research on DSM generation technology based on video satellite images[D]. Wuhan: Huazhong University of Science and Technology, 2019. |
| [13] |
CHERNETSKIY M, TAO Y, MULLER J P. 3D stereo reconstruction: high resolution satellite video[C]//Proceedings of 2019 SPIE International Society for Optical Engineering. Strasbourg: SPIE, 2019: 582-593.
|
| [14] |
王少威. 卫星视频影像建筑高度提取方法研究[D]. 武汉: 华中科技大学, 2018. WANG Shaowei. Research on building height extraction method of satellite video images[D]. Wuhan: Huazhong University of Science and Technology, 2018. |
| [15] |
罗亦乐, 梁艳平, 王妍. 基于光流法的卫星视频交通流参数提取研究[J]. 计算机工程与应用, 2018, 54(10): 204-207, 255. LUO Yile, LIANG Yanping, WANG Yan. Traffic flow parameter estimation from satellite video data based on optical flow[J]. Computer Engineering and Applications, 2018, 54(10): 204-207, 255. DOI:10.3778/j.issn.1002-8331.1612-0537 |
| [16] |
赵旭辉. SLAM技术在视频卫星处理中的应用研究[D]. 武汉: 武汉大学, 2019. ZHAO Xuhui. Application research of SLAM in video satellite processing[D]. Wuhan: Wuhan University, 2019. |
| [17] |
李建国, 杨保河, 石胜斌. 遥感视频卫星多目标检测、跟踪和定位算法[J]. 火力与指挥控制, 2021, 46(2): 114-119. LI Jianguo, YANG Baohe, SHI Shengbin. Multi-object detection locationing and locating algorithm for remote sensing video satellites[J]. Fire Control & Command Control, 2021, 46(2): 114-119. |
| [18] |
朱泽尧, 胡庆武, 王玥, 等. 基于吉林一号视频卫星影像的实时车辆跟踪方法研究[J]. 武汉理工大学学报(交通科学与工程版), 2021, 45(4): 655-660. ZHU Zeyao, HU Qingwu, WANG Yue, et al. Research on real-time vehicle tracking method based on Jilin-1 video satellite imagery[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2021, 45(4): 655-660. DOI:10.3963/j.issn.2095-3844.2021.04.008 |
| [19] |
张过. 卫星视频处理与应用进展[J]. 应用科学学报, 2016, 34(4): 361-370. ZHANG Guo. Satellite video processing and applications[J]. Journal of Applied Sciences, 2016, 34(4): 361-370. DOI:10.3969/j.issn.0255-8297.2016.04.001 |
| [20] |
LIU Zikun, HU Jingao, WENG Lubin, et al. Rotated region based CNN for ship detection[C]//Proceedings of 2017 IEEE International Conference on Image Processing. Beijing: IEEE, 2017: 900-904.
|
| [21] |
LIU Lei, PAN Zongxu, LEI Bin. Learning a rotation invariant detector with rotatable bounding box[EB/OL]. [2023-09-15]. https://arxiv.org/abs/1711.09405.
|
| [22] |
CUI Yanyu, HOU Biao, WU Qian, et al. Remote sensing object tracking with deep reinforcement learning under occlusion[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 60: 1-13. |
| [23] |
HU Zhongyi, ZOU Mianzu, CHEN Changzu, et al. Tracking via context-aware regression correlation filter with a spatial-temporal regularization[J]. Journal of Electronic Imaging, 2020, 29(2): 023029. |
| [24] |
XUAN Shiyu, LI Shengyang, HAN Mingfei, et al. Object tracking in satellite videos by improved correlation filters with motion estimations[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 58(2): 1074-1086. |
| [25] |
ZHANG Wenhua, JIAO Licheng, LIU Fang, et al. MBLT: learning motion and background for vehicle tracking in satellite videos[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 60: 1-15. |
| [26] |
SHAO Jia, DU Bo, WU Chen, et al. Tracking objects from satellite videos: a velocity feature based correlation filter[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(10): 7860-7871. DOI:10.1109/TGRS.2019.2916953 |
| [27] |
HAN Yuqi, WANG Hongshuo, ZHANG Zengshuo, et al. Boundary-aware vehicle tracking upon UAV[J]. Electronics Letters, 2020, 56(17): 873-876. DOI:10.1049/el.2020.1170 |
| [28] |
HAN Yuqi, DENG Chenwei, ZHAO Baojun, et al. State-aware anti-drift object tracking[J]. IEEE Transactions on Image Processing, 2019, 28(8): 4075-4086. DOI:10.1109/TIP.2019.2905984 |
| [29] |
DENG Chenwei, HE Shuangcheng, HAN Yuqi, et al. Learning dynamic spatial-temporal regularization for UAV object tracking[J]. IEEE Signal Processing Letters, 2021, 28: 1230-1234. DOI:10.1109/LSP.2021.3086675 |
| [30] |
SHAO Jia, DU Bo, WU Chen, et al. Can we track targets from space? A hybrid kernel correlation filter tracker for satellite video[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(11): 8719-8731. DOI:10.1109/TGRS.2019.2922648 |
| [31] |
WU Jialian, SU Xin, YUAN Qiangqiang, et al. Multivehicle object tracking in satellite video enhanced by slow features and motion features[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 60: 1-26. |
| [32] |
WANG Qiang, ZHANG Li, BERTINETTO L, et al. Fast online object tracking and segmentation: a unifying approach[C]//Proceedings of 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019: 1328-1338.
|
| [33] |
YANG Xue, YAN Junchi. Arbitrary-oriented object detection with circular smooth label[C]//Proceedings of 2020 European Conference on Computer Vision. Berlin: Springer, 2020: 677-694.
|
| [34] |
岳琪琪. 基于深度学习的尺度与角度自适应海面目标跟踪算法[D]. 上海: 上海大学, 2021. YUE Qiqi. Adaptive scale and angle for sea surface object tracking based on deep learning[D]. Shanghai: Shanghai University, 2021. |
| [35] |
LI Yang, ZHU Jianke, HOI S C H, et al. Robust estimation of similarity transformation for visual object tracking[C]//Proceedings of 2019 AAAI Conference on Artificial Intelligence. Menlo Park: AAAI Press, 2019: 8666-8673.
|
| [36] |
李忠新, 茅耀斌, 王执铨. 基于对数极坐标映射的图像拼接方法[J]. 中国图象图形学报, 2005, 10(1): 59-63. LI Zhongxin, MAO Yaobin, WANG Zhiquan. A method of image mosaicing using log polar coordinate mapping[J]. Journal of Image and Graphics, 2005, 10(1): 59-63. |
| [37] |
DANELLJAN M, BHAT G, KHAN F S, et al. ECO: efficient convolution operators for tracking[C]//Proceedings of 2017 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017: 6931-6939.
|
| [38] |
汪韬阳. 光学卫星视频数据处理与应用[M]. 北京: 科学出版社, 2020. WANG Taoyang. Processing and application of optical satellite video data[M]. Beijing: Science Press, 2020. |
| [39] |
张过, 蒋永华, 汪韬阳, 等. 高分辨率视频卫星标准产品分级体系[M]. 北京: 科学出版社, 2017. ZHANG Guo, JIANG Yonghua, WANG Taoyang, et al. Standard product grading system for high resolution video satellites[M]. Beijing: Science Press, 2017. |
| [40] |
张过. 缺少控制点的高分辨率卫星遥感影像几何纠正[D]. 武汉: 武汉大学, 2005. ZHANG Guo. Rectification for high resolution remote sensing image under lack of ground control points[D]. Wuhan: Wuhan University, 2005. |
| [41] |
王霞, 张过, 沈欣, 等. 顾及像面畸变的卫星视频稳像[J]. 测绘学报, 2016, 45(2): 194-198. WANG Xia, ZHANG Guo, SHEN Xin, et al. Satellite video stabilization with geometric distortion[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(2): 194-198. DOI:10.11947/j.AGCS.2016.20150238 |
| [42] |
FISCHLER M A, BOLLES R C. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography[J]. Communications of the ACM, 1981, 24(6): 381-395. |
| [43] |
DANELLJAN M, ROBINSON A, KHAN F S, et al. Beyond correlation filters: learning continuous convolution operators for visual tracking[C]//Proceedings of 2016 European Conference on Computer Vision. Berlin: Springer, 2016: 472-488.
|
| [44] |
DANELLJAN M, KHAN F S, FELSBERG M, et al. Adaptive color attributes for real-time visual tracking[C]//Proceedings of 2014 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Columbus: IEEE, 2014: 1090-1097.
|
| [45] |
WANG Yanbo, WANG Fasheng, WANG Chang, et al. Learning saliency-aware correlation filters for visual tracking[J]. The Computer Journal, 2022, 65(7): 1846-1859. |
| [46] |
HENRIQUES J F, CASEIRO R, MARTINS P, et al. High- speed tracking with kernelized correlation filters[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 37(3): 583-596. |
| [47] |
HENRIQUES J F, CASEIRO R, MARTINS P, et al. Exploiting the circulant structure of tracking-by-detection with kernels[C]//Proceedings of 2012 European Conference on Computer Vision. Berlin: Springer, 2012: 702-715.
|
| [48] |
LI Feng, TIAN Cheng, ZUO Wangmeng, et al. Learning spatial-temporal regularized correlation filters for visual tracking[C]//Proceedings of 2018 IEEE Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 4904-4913.
|
| [49] |
GALOOGAHI H K, FAGG A, LUCEY S. Learning background- aware correlation filters for visual tracking[C]//Proceedings of 2017 IEEE International Conference on Computer Vision. Venice: IEEE, 2017: 1144-1152.
|
| [50] |
XU Tianyang, FENG Zhenhua, WU Xiaojun, et al. Learning adaptive discriminative correlation filters via temporal consistency preserving spatial feature selection for robust visual object tracking[J]. IEEE Transactions on Image Processing, 2019, 28(11): 5596-5609. |
| [51] |
BERTINETTO L, VALMADRE J, GOLODETZ S, et al. Staple: complementary learners for real-time tracking[C]//Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016: 1401-1409.
|
| [52] |
ZHAO Manqi, LI Shengyang, XUAN Shiyu, et al. SatSOT: a benchmark dataset for satellite video single object tracking[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-11. |
| [53] |
WU Yi, LIM J, YANG M H. Online object tracking: a benchmark[C]//Proceedings of 2013 IEEE Conference on Computer Vision and Pattern Recognition. Portland: IEEE, 2013: 2411-2418.
|
| [54] |
WU Yi, LIM J, YANG M H. Object tracking benchmark[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(9): 1834-1848. |


