2. 自然资源部超大城市自然资源时空大数据分析应用重点实验室, 上海 200063;
3. 上海市测绘院, 上海 200063
2. Key Laboratory of Spatial-Temporal Big Data Analysis and Application of Natural Resources in Megacities, MNR, Shanghai 200063, China;
3. Shanghai Surveying and Mapping Institute, Shanghai 200063, China
近几十年来,全球范围内普遍出现高速城镇化现象,土地城镇化速度远大于人口城镇化速度,城镇用地无序蔓延且集约利用程度低,生态环境退化、自然资源枯竭和耕地破坏更是时有发生[1-2]。新时代国土空间规划亟须真实模拟推演未来规划实施情景,以便对国土空间利用进行评估及优化调控。因此,更加准确地模拟土地利用变化过程并深入理解土地利用变化时空模式对于土地管理者和城市规划决策者是必不可少的[3]。元胞自动机因其开放式的结构,可以与其他模型集成耦合来进行复杂非线性系统的时空演变的模拟[4],在城市扩展和土地利用演变模拟中取得了显著成就[5-6]。
研究人员提出一系列基于元胞自动机(cellular automata, CA)的模型用于城市扩展模拟,与机器学习耦合使用的学习模型包括支持向量机-元胞自动机(SVM-CA)、人工神经网络-元胞自动机(ANN-CA)、地理加权人工神经网络-元胞自动机(GWANN-CA)和随机森林-元胞自动机(RF-CA)[7-10]等,这些方法能够有效挖掘城镇扩展的非线性特征,从而构建其非线性驱动机制,有助于提高模拟精度; 此外,还有逻辑回归-元胞自动机(LR-CA)、CA-Markov和最大熵-元胞自动机(ME-CA)等机理模型[11-12],对获得的驱动机制有明确解释,但对城市扩展过程的非线性特征解释不足。以上这些CA模型共同存在一些不足,难以实现CA对城市扩展的真实模拟,不足之处主要体现在:①模型构建时对邻域空间的多尺度特征表达不足。城市土地元胞状态的变化不仅仅受到自身单个元胞信息的影响,相邻元胞的空间变量信息也在不同尺度上通过不同的特征效应影响元胞状态的改变,少有研究完整地表达城市土地利用演变的多尺度空间邻域效应影响。②转换规则的构建没有顾及长时间序列的时间依赖性影响,即没有考虑城市历史空间变量影响(时间依赖性)。城市土地利用变化从历史过程上看,是具有趋势性的,受政治、经济、自然、文化等历史因素的影响,目前学者对城市扩展模拟多基于马尔可夫过程,认为城市扩展仅受上一时态土地利用及驱动因素影响[13],对长时序下的时间依赖性挖掘不足。
具有深度和广度的神经网络,作为机器学习的一个子领域,被称为深度学习(deep learning, DL),逐渐在城市扩展模拟中得到重视。卷积神经网络(convolutional neural network, CNN)是一种深度学习网络,它可以考虑空间效应,通过卷积运算提取局部驱动因子空间特征,从而获得准确土地利用演变结果[14]。文献[15]耦合多驱动因子构建元胞多维向量,提出了顾及空间邻近地块间驱动效应的CNN-VCA(vector-based cellular automata)模型。针对土地利用演化的多尺度特性,文献[16]提出基于多结构卷积神经网络(multi-structure convolutional neural network, MSCNN)的MSCNN-CA模型,相比单结构卷积神经网络CA模型具有更高的准确度和稳健性,但多结构卷积使得参数量成倍增多,效率不高。目前有学者通过构造不同大小卷积核从驱动因子层面提取城市扩展的空间多尺度邻域效应,还有学者通过构建双尺寸邻域[17]来解决邻域大小选择的矛盾,但都只考虑了单一时态下的空间多尺度邻域效应; 三维卷积神经网络(three-dimensional convolutional neural network, 3DCNN)是CNN的扩展,通过增加卷积核的维度,可以对多期城市扩展相关数据沿着时间维度进行空间信息的提取,本文拟将元胞的近邻范围空间变量和非近邻空间变量对元胞状态改变的不同空间效应信息(多尺度)挖掘融合,从而使转换规则的提取更加可靠。长短期记忆(long short term memory, LSTM)是另一种深度神经网络,可以稳定地捕获长期模式,让需要的历史信息传递下去,从而避免了“梯度问题”[18]。卷积长短期记忆(convolution LSTM, ConvLSTM)[19]是全连接LSTM的改进版,将全连接运算符替换为卷积运算符,在将历史信息过滤传递下去的同时,保留了数据即二维图像的空间信息,适用城市扩展模拟所需时空信息的提取融合。
综上,本文提出一种顾及空间多尺度邻域效应(3DCNN)和时间依赖性(ConvLSTM)的城市扩展深度学习CA模型(下文称“Deep-CA”),通过组合普通卷积和空洞卷积的3DCNN沿时间维度挖掘不同空间尺度下的邻域效应,普通卷积层用于提取建模元胞的近距离空间邻域效应,而空洞卷积通过设置间隔的方式可以获得更大的邻域范围,在保证模型运行效率的同时,最终实现元胞多尺度邻域特征的聚合。对挖掘得到的空间特征图通过ConvLSTM实现时间和空间信息的过滤融合, 得到影响未来城市土地利用变化的时空依赖性信息,经由全连接网络,得到城市扩展的转换规则。该模型使得CA转换规则的挖掘提取更加完善可靠,为城市扩展提供更加准确可靠的模拟方法。
1 研究区与数据集北京市是我国的首都、直辖市、国家中心城市、超大城市,国务院批复确定的我国政治中心、文化中心、国际交往中心、科技创新中心,吸引了大量人口流入,城镇化进程迅速,其位置如图 1(a)所示。截至2020年,全市下辖16个区,总面积16 410.54 km2。根据第七次人口普查数据,截至2021年末,北京市常住人口为2 188.6万人。近几十年来,由于交通的不断改善和政府政策的推出完善,北京市经济快速发展,人口不断增加,城市迅速扩展(图 1(b)),不可避免产生交通拥堵、环境恶化、住房困难等“大城市病”。为了遏制城市无序蔓延,集约节约利用土地,有必要了解城市扩展的时空依赖性对城市土地演变的影响,有利于真实展现城市未来用地变化,为政府合理规划城市新用地、限制城市用地盲目增长提供借鉴。
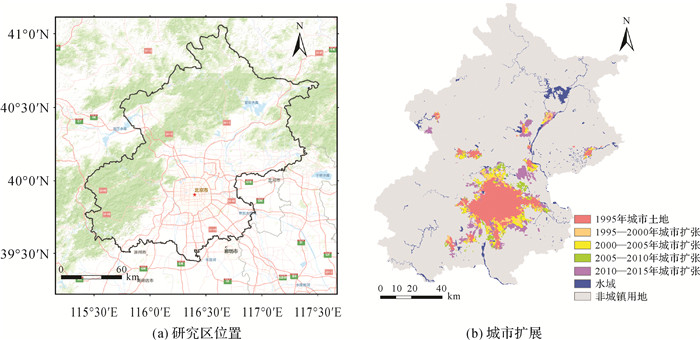
|
| 图 1 北京市位置和1995—2015年每5年城市扩展 Fig. 1 The location of Beijing and the urban growth of Beijing each five-years period from 1995 to 2015 |
图 1(b)为1995—2015年的北京市城市用地扩展图。相关研究表明,制度结构、社会经济因素、人口密度、邻里因素和邻近性等是城市扩展的主要驱动因素[20-22]。因此,结合研究区实际情况及数据的可得性,本文选取11个驱动因素来构建城市扩展模型,其中DEM和坡度数据用于表征地表状况;GDP和人口密度(population, POP)表征社会经济因素;道路、城市土地和POI数据用于计算邻近效应,得到距城市用地距离、距国道距离、距省道距离、距县道距离、距高速距离、距铁路距离、距县级行政中心距离7个基于距离的驱动变量。所有城市增长驱动变量处理和可视化(图 2)在ArcGIS 10.7中进行。本文所需数据及其处理说明见表 1,包括土地利用数据、POI数据、交通道路数据、社会经济数据和DEM数据等。1995—2015年,每5年为一个时期。社会经济数据包括GDP和人口,DEM数据用于计算坡度和高程,道路和POI数据用于获得欧氏距离变量数据。所有数据栅格化后均被重采样至30 m的空间分辨率,且保持坐标、投影和位置一致。北京市用地类型分为城市、非城市用地和水域3类用地。
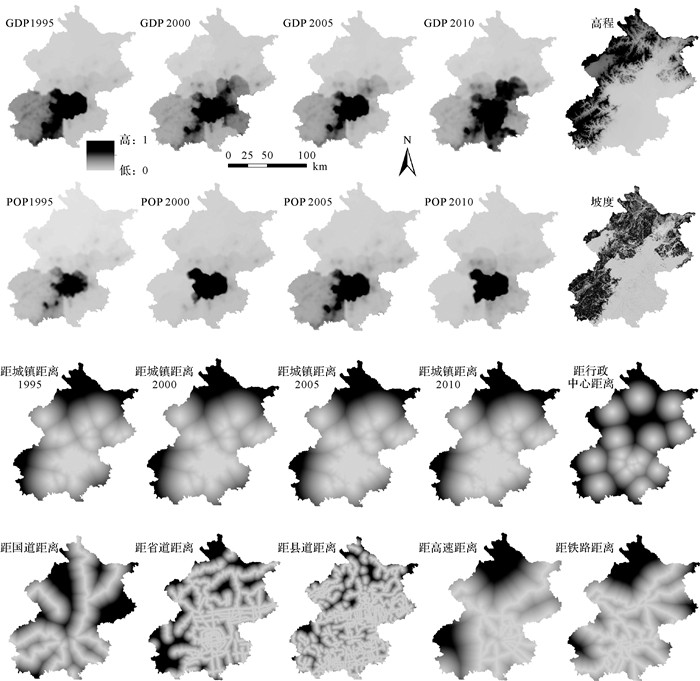
|
| 图 2 北京市城市扩展驱动因素 Fig. 2 Driving factors of urban growth in Beijing |
| 数据类型 | 年份 | 数据处理说明 | 来源 |
| 土地利用数据 | 1995、2000、2005、2010、2015 | 共有6大类地,重分类为城市用地、非城市用地和水域,分辨率30 m | 中国科学院资源环境科学数据中心(http://www.resdc.cn) |
| 社会经济数据 | 1995—2015 | GDP和POP, 每5年一张栅格图(1 km×1 km),ArcGIS栅格转点后克里金插值至30 m×30 m | |
| 道路数据 | 2015 | 包括国道、高速、铁路、主要道路等shp格式数据(唯一可获取年份),欧氏距离处理为分辨率30 m的栅格数据 | 中国科学院资源环境科学数据中心(http://www.resdc.cn) |
| DEM数据 | 2015 | NASA DEM,分辨率30 m, 可用于计算坡度 | https://earthdata.nasa.gov/ |
| POI数据 | 2019 | 县行政中心,欧氏距离处理(30 m栅格) | 爬取(https://www.baidu.com/) |
2 研究方法
本文具体研究思路为:①使用普通卷积和空洞卷积组合的3DCNN沿时间维度挖掘不同空间尺度下的邻域效应,普通卷积层用于提取建模元胞的近距离空间邻域效应,而空洞卷积通过其设置间隔的方式可以获得更大的邻域范围,在保证模型运行效率的同时,实现多尺度邻域特征的聚合。②将得到的空间多尺度邻域特征图进一步提取得到影响未来城市土地利用变化的时间依赖性信息。本文通过构建ConvLSTM神经网络挖掘时间依赖性信息,最终输出时空信息同化的特征图;将提取融合的最终信息输入全连接层,得到元胞转换概率。③深度学习网络与CA基本框架耦合,构建顾及空间多尺度邻域效应和时间依赖性的时空CA模型。
2.1 深度学习模型 2.1.1 3DCNN用于空间多尺度邻域效应提取3DCNN沿着时间和空间维度进行3D卷积运算,由于在计算机视觉研究中很少考虑时间维度,城市土地利用演变模拟时也很少充分考虑时间维度,导致它不像2DCNN那样应用广泛[23],但是3DCNN已被证实更加适合时空呈现[24]。土地利用遥感数据及其驱动数据通常包含时空信息(特征),3DCNN可以有效挖掘利用这些信息(特征)。例如,城市不同时期的道路因素都会对未来城市土地利用变化产生一定影响。3DCNN可沿着时间维度对空间信息进行特征提取,非常适合用于城市扩展空间特征挖掘,同时,它的特征提取能力也更加可靠强大。
3DCNN的卷积层网络的卷积运算如式(1)所示[25]
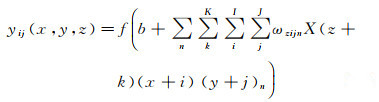 (1)
(1)
式中,f为激活函数;b为偏置;yij(x, y, z)为卷积层输出值;K、I、J为卷积核维度,其中I、J分别表示核的宽度和高度,K为沿时间维度的核大小;ωzijn为上一卷积层或池化层输出的第n个特征图上(K,I,J)位置所对应的权重;X为输入的三维数据。
从特定特征图局部邻域提取特征由3D卷积滤波器执行,并添加偏置,结果加激活函数。
在本文提出的模型中,3DCNN通过组合使用普通卷积和空洞卷积,从城市扩展驱动因素中提取空间多尺度邻域效应;两者的二维运算结构如图 3所示,普通卷积层用于提取土地元胞的近距离空间邻域效应,空洞卷积以设置间隔的方式将卷积计算作用于非连续空间单元,扩大邻域效应范围,实现多尺度邻域效应的聚合。实际生活中,时间图像(视频)是由多光谱(多波段)通道组成,维度包括空间、时间和光谱维度,类比到本文为空间、时间和驱动因子个数,由此所需数据类型为4D张量,由于深度学习模型训练分批次进行训练,因此添加一个batch(批)维度,最终模型输入数据为“批尺寸×时间×特征×高度×宽度”的5D张量,形状为(b,t,c,h,w),本文中批次最终设置为32,数据期数为4,驱动因子个数11,影响元胞空间大小为31×31,即(32, 4, 11, 31, 31)。
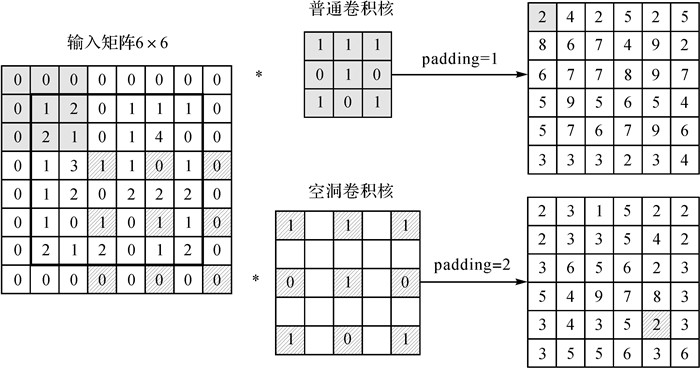
|
| 图 3 普通卷积和空洞卷积运算 Fig. 3 Ordinary convolution and hole convolution operations |
2.1.2 历史时空信息同化的ConvLSTM网络
LSTM网络可以保持早期观察序列中的相关信息,同时消除不相关信息,更重要的是,它克服了传统模型存在的过度拟合、梯度爆炸和消失问题[18]。LSTM网络将展平的特征图作为输入,通过全连接的层进行编码,不可避免丢失了空间相关信息。ConvLSTM将LSTM中的全连接运算符替换为卷积运算符(图 4),保证空间特征图大小不变,进行时空信息的过滤融合输出,以更少的参数为模型增加了更多的计算能力。ConvLSTM的体系结构可以表达为式(2)—式(7)[19]
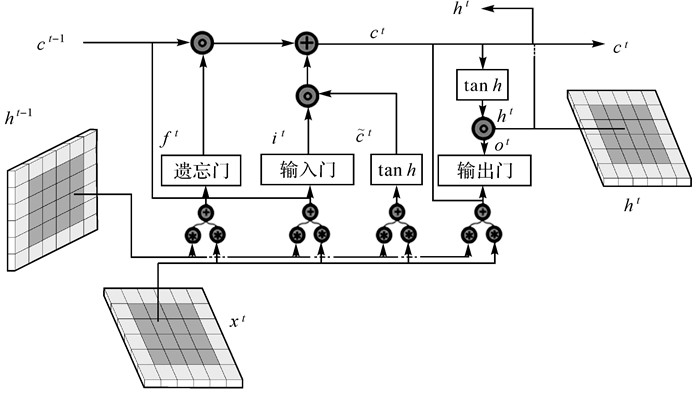
|
| 图 4 卷积LSTM基本结构 Fig. 4 The basic structure of ConvLSTM |
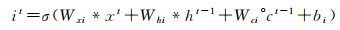 (2)
(2)
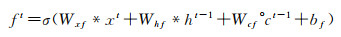 (3)
(3)
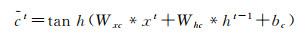 (4)
(4)
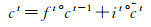 (5)
(5)
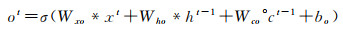 (6)
(6)
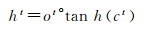 (7)
(7)
式中,*为卷积算子;σ为sigmoid激活函数;°表示哈达玛积,单元状态由c1,c2,…,ct表示,隐藏状态由h1,h2,…,ht表示;it、ft、ot分别表示输入门输出门和遗忘门输出结果;Wxi、Whi、Wci、Wxf、Whf、Wcf、Wxo、Who、Wco、Wxc和Whc为二维卷积核权重;bi、bf、bc和bo是偏置项。
2.2 城市扩展时空CA模型构建(Deep-CA)本文使用深度学习模型(即3DCNN-ConvLSTM)预测2010—2015年北京市非城市变为城市用地的转换概率,最终获得开发适宜性图层导入CA模型中进行城市扩展模拟。CA模型中元胞的最终转换概率由式(8)计算得出(由于后续试验中涉及不同模型精度对比,暂不将随机效应纳入转换规则)
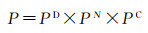 (8)
(8)
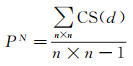 (9)
(9)
 (10)
(10)
式中,P为最终转换概率;PD是深度学习模型考虑历史驱动因素得到的开发适宜性概率;PN表示邻域配置的影响,用于约束城市形态和接收周围元胞影响[17];n表示邻域大小;d表示领域单元与中心单元之间的距离(d=1, 2, 3, …, (n+1)/2);CS(d)表示距离为d时的邻域单元状态函数,如果元胞状态为城市则返回1,否则,返回0;PC为约束因素,当元胞为城市元胞或为水域元胞时,CON()返回0,其他,返回1。
2.3 评价指标为了评估模拟的城市扩展准确度,参考相关文献,选择整体准确度(overall accuracy, OA)、Kappa系数[26]和品质因数(figure of merit, FoM)[27]来评估所提出的CA模型的模拟能力,OA、Kappa和FoM的取值范围均在0~1之间,其值越大,模拟结果越好。其中,Kappa系数是衡量土地利用模拟与观测之间数量一致性的常用方法;FoM侧重于衡量模拟和观测之间变化一致性的高低。命中率h(表示模拟为城市元胞且实际为城市元胞的数目占元胞总数的比例)和错误率c(表示模拟为非城市元胞但实际为城市元胞的数目占元胞总数的比例)也将用于模型评价。OA、Kappa和FoM的计算公式分别为
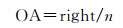 (11)
(11)
 (12)
(12)
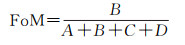 (13)
(13)
式中,right为模拟正确的元胞数量;n为所有元胞的总数量;a0和a1分别为观测结果中城市元胞和非城市元胞的数量;b0和b1分别为模拟结果中城市元胞和非城市元胞的数量;A为观测为变化但模拟为保持不变的元胞数量;B为在观测和模拟中均为城市扩展的元胞数量;C为观测为城市扩展但模拟为其他地类转换的元胞数量,本文只考虑非城市向城市用地的转变,则C为0;D为观测为非城市但模拟为城市扩展的元胞数量。
此外,还使用一组景观指数来评估实际和模拟城市土地之间的景观格局相似性,从密度大小及差异、邻近度指标、形状指标和面积指标分别选择斑块数量(number of patches,NP)、平均欧几里得最邻近距离(Euclidean nearest neighbor index, ENN_MN)、平均形状指标(shape index, SHAPE_MN)和最大斑块占景观面积比(largest patch index, LPI)共4个景观指标[28-29],其中NP用于衡量斑块数量,ENN_MN衡量斑块分布,SHAPE_MN衡量斑块形状复杂度,LPI表征主要斑块优势度,所有景观指标通过Fragstats 4.2计算[30]。相似性计算公式[31]为
 (14)
(14)
 (15)
(15)
式中,Isi和Ioi分别为模拟城市土地和实际城市土地的第i个景观指标的值;ΔIi为第i对模拟和实际景观指标的归一化差,LPI的原始单位已经是百分比,因此LPI的ΔIi为差的绝对值;γI为实际和模拟城市土地之间的景观格局相似性;n为景观指标的个数;ENNMN为平均欧几里得最邻近距离;SHAPEMN为平均形状指标。
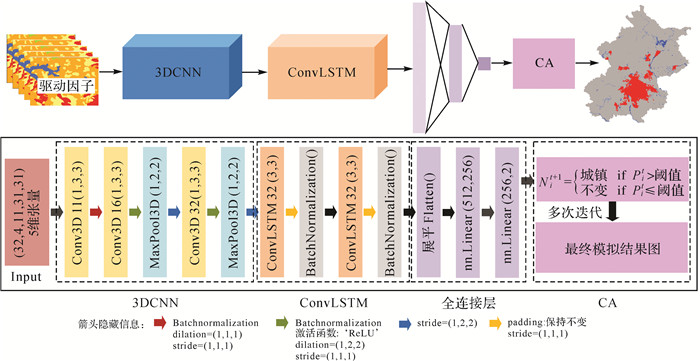
3 试验与分析 3.1 模型结构及试验细节Deep-CA模型的构建和运行均在Python 3.7环境下实现,Pytorch作为后端[32],同时也使用了Numpy、Visdom和Gdal等Python库。计算机配置为Intel i7-10代,16 GB内存,4 GB GTX 1650 Ti显卡,模型训练和运行采用GPU并行加速。对于训练过程,测试了16、32和64的不同批次处理以提高模型性能,发现批大小为32时训练效果最好,且发现模型至少迭代90次才能收敛,为了保证模型的精度和效率,训练代数最终设置为110。选择了学习率为0.000 1的Adam优化器[33],和交叉熵[34]作为损失函数,并在验证集上使用提前停止法(Early Stopping)防止模型过度拟合,即泛化能力过低。经过多次调试,模型最终结构如图 5所示,模型结构中,加入批标准化层和Dropout正则化层,也可起到防止过拟合的作用。模型的训练曲线如图 6所示,在早期,可以看到验证集准确度迅速提高,在达到0.95左右时,准确度的变化会减慢,但仍继续增加,达到的最高准确度为0.975,也是模型的提前停止点;损失函数值随着代数增加整体下降,表示误差逐渐最小化。
|
| 图 5 Deep-CA模型结构 Fig. 5 The structure of Deep-CA model |

|
| 图 6 Deep-CA模型训练曲线 Fig. 6 Training curve of the Deep-CA model |
模型结构为3DCNN、ConvLSTM、全连接层和CA的组合,以提高城市模拟的精度。ConvLSTM连接到3个3DCNN块,3DCNN沿着时间维度在不同卷积尺度上进行严格的空间特征提取,3DCNN对输入的样本图像执行多步卷积、批标准化和最大池化操作,将提取得到的空间多尺度邻域特征图输送到ConvLSTM块,ConvLSTM接收到特征图后,执行更严格的时空特征提取。最后,最终特征图展平以后被输入到具有512个神经元全连接层,经过多个全连接层输出最终概率值。层与层之间使用概率为0.5的dropout层[35],以避免过度拟合。将综合得到的概率图(式(8))输入CA模块中,多次迭代,每次迭代按照变化元胞个数从已排序的概率中找到元胞是否变化的阈值作为判断条件。
本文选择北京市20年数据(1995—2015年,每5年为一期)进行模型的训练验证,1995—2010年数据用于训练,2015年数据用于测试训练的模型。为了避免空间自相关影响以及兼顾模型的效率和性能,随机抽样30 000个样本,正负样本各占50%,其中样本集80%用于训练,余下20%验证集用于调整模型超参数和检查停止条件。
为了验证所提模型的优势,本文选择了代表机理CA模型的LR-CA、ME-CA和代表学习模型的ANN-CA与本文的Deep-CA进行比较,这些模型均选择北京市2010和2015年数据,未考虑空间效应和时间依赖性。本文各CA模型最终参数设置如下:转换概率为各模型得到的开发适宜性图集;半年迭代一次,2010—2015年共迭代10次;邻域选择7×7的摩尔型邻域;生态规划限制设置为水体不能被侵占;本文不考虑随机扰动因素影响。
3.2 模型对比分析表 2列出了传统模型LR-CA、ME-CA、机器学习ANN-CA与顾及空间多尺度邻域效应与时间依赖性的Deep-CA在测试数据(2015年)上的预测结果。
| 模型 | OA | Kappa | FoM | h/(%) | c/(%) |
| Deep-CA | 0.971 | 0.855 | 0.304 | 1.28 | 1.46 |
| ANN-CA | 0.968 | 0.843 | 0.267 | 1.19 | 1.55 |
| ME-CA | 0.969 | 0.846 | 0.278 | 1.16 | 1.59 |
| LR-CA | 0.968 | 0.841 | 0.264 | 1.14 | 1.60 |
表 2表明,与其他模型相比,Deep-CA模型明显提高了模拟精度,各个指标都有不同程度提高, 特别是FoM达到0.304,提高了约4%,从而验证了时空依赖性对城市扩展具有重要影响。模型精度没有提升过高原因推测为反映历史情况的驱动数据不够完善,道路数据只有近期道路,存在噪声影响情况,但Deep-CA可以在学习过程中识别噪声并加以修正或剔除,从而保证模型精度,从这里也可以看出Deep-CA强大的学习能力。
本文还结合NP、ENN_MN、SHAPE_MN和LPI 4个景观指标,评价了模拟城市土地与实际城市土地的全局景观相似性。表 3显示了4个模型的景观相似度的计算结果。与ANN-CA、ME-CA和LR-CA相比,Deep-CA模型与实际城市土地的景观相似性最高(0.871),说明Deep-CA对城市形态有更好的控制。
| 模型 | 景观指标 | 相似性 | |||
| NP | ENN_ MN/m | SHAPE_ MN | LPI /(%) | ||
| 实际城市土地 | 52 | 1 073.234 | 2.031 | 4.777 | - |
| Deep-CA | 58 | 1 141.205 | 1.349 | 4.781 | 0.871 |
| ANN-CA | 24 | 3 288.405 | 1.522 | 4.829 | 0.274 |
| ME-CA | 42 | 1 412.996 | 1.378 | 4.833 | 0.779 |
| LR-CA | 27 | 2 835.704 | 1.496 | 4.789 | 0.400 |
图 7左侧显示了北京市2015年Deep-CA的模拟结果,为了更直观展示不同模型模拟结果局部差异,兼顾城市扩展类型,在研究区选择6个不同大小的局部区域,将各个模型得到的模拟结果与实际结果进行对比。可以看出Deep-CA对城市增长有更精细的控制,模拟结果边缘更接近现实,证明了空间多尺度邻域效应和时间依赖性对城市增长形态的影响。具体来看,对于填充式城市扩展(图 7(a)、(d)),Deep-CA效果最好,ME-CA次之,LR-CA和ANN-CA仍为边缘式扩展,填充不够彻底;由图 7(b)、(c)、(e)、(f)可看出,Deep-CA对城市边缘约束更好,未出现盲目沿城市边缘扩展情况。
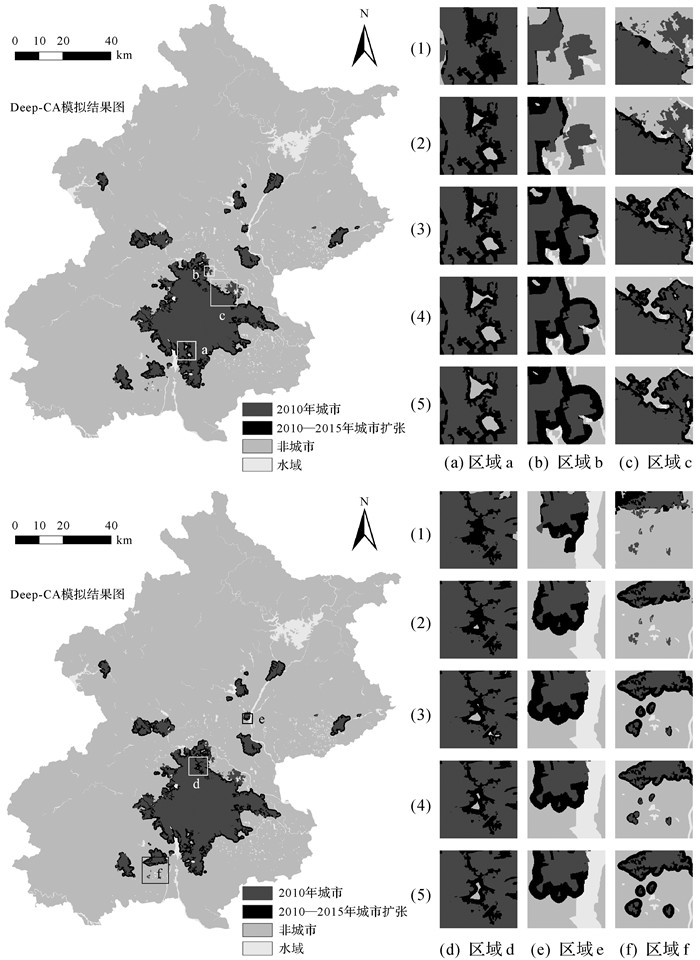
|
| 注:(1)为实际城市扩展,(2)—(5)分别为使用Deep-CA、ME-CA、ANN-CA、LR-CA得到的模拟结果。 图 7 模拟结果与实际的局部对比 Fig. 7 Local comparison between the simulated results and reality |
4 结论与讨论
本文提出了一种结合深度学习提取空间多尺度邻域效应和长时间序列时间依赖性特征的城市扩展元胞自动机模型(Deep-CA)。3DCNN和ConvLSTM首次用于城市扩展模拟,抛开了城市扩展模拟的Markov假设前提,即只关注研究时间段的起点和终点,将长时间序列数据的时间依赖性特征考虑进城市扩展模拟。3DCNN沿着时间维度在不同卷积尺度上进行严格的空间邻域特征提取,ConvLSTM对3DCNN提取空间特征图进行更严格的时空特征提取,对时间和空间信息进行同化输出,从而更加准确仿真城市土地利用变化。以北京市作为研究区,验证所提出的Deep-CA模型性能。试验表明,与传统模型相比,从模拟精度上看,Deep-CA模型的预测准确率最高,OA为0.971,Kappa系数为0.855,FoM指数为0.304,h为1.28%,c为1.46%;从构建的景观格局相似性上看,Deep-CA景观相似性最大,为0.871;从模拟局部形态上看,Deep-CA填充式扩展模拟效果最好,对城市边缘形态约束也更优。综上,与其他CA模型(LR-CA、ANN-CA和MN-CA)相比,Deep-CA模型能够获得最佳的仿真结果。
本文所提出的Deep-CA模型需要在长时间土地利用数据和驱动因子数据支撑下使用,受计算机内存限制,研究区尺度为市域,未来可以优化算法或扩大运行内存使其可以在更大尺度上进行模拟。Deep-CA模型同样存在其局限性:①由于考虑历史因素致使数据集成倍增加,考虑计算机性能,驱动因素不能过多选择,未来可以适当加入其他重要因素,如距车站距离、距医院距离、距停车场距离等基于POI获得的变量。②该模型属于深度学习模型,虽然可以很好捕捉城市扩展的非线性特征,但无法像机理模型解析各个驱动因子对城市扩展的影响程度。使用更加完善的驱动因素数据以及解析城市扩展机理将成为下一步工作的重点。③城市扩展受城市规划和政府政策的影响,将政策融入到Deep-CA模型中也是未来工作之一。
| [1] |
焦利民, 董婷, 谷岩岩. 2000-2012年中国地级以上城市空间弹性分析[J]. 资源科学, 2016, 38(7): 1254-1265. JIAO Limin, DONG Ting, GU Yanyan. The spatial resilience of prefecture-level cities in China from 2000 to 2012[J]. Resources Science, 2016, 38(7): 1254-1265. |
| [2] |
DANIS H, ULUCAK R, KHAN S U D. Determinants of the ecological footprint: role of renewable energy, natural resources, and urbanization[J]. Sustainable Cities and Society, 2020, 54: 101996. DOI:10.1016/j.scs.2019.101996 |
| [3] |
VAN VLIET J, BREGT A K, BROWN D G, et al. A review of current calibration and validation practices in land-change modeling[J]. Environmental Modelling & Software, 2016, 82: 174-182. |
| [4] |
ROODPOSHTI M S, ARYAL J, BRYAN B A. A novel algorithm for calculating transition potential in cellular automata models of land-use/cover change[J]. Environmental Modelling & Software, 2019, 112: 70-81. |
| [5] |
WANG Yang, LI Shuangcheng. Simulating multiple class urban land-use/cover changes by RBFN-based CA model[J]. Computers & Geosciences, 2011, 37(2): 111-121. |
| [6] |
SANTÉ I, GARCÍA A M, MIRANDA D, et al. Cellular automata models for the simulation of real-world urban processes: a review and analysis[J]. Landscape and Urban Planning, 2010, 96(2): 108-122. DOI:10.1016/j.landurbplan.2010.03.001 |
| [7] |
KARIMI F, SULTANA S, BABAKAN A S, et al. An enhanced support vector machine model for urban expansion prediction[J]. Computers, Environment and Urban Systems, 2019, 75: 61-75. DOI:10.1016/j.compenvurbsys.2019.01.001 |
| [8] |
XU Tingting, GAO J, COCO G. Simulation of urban expansion via integrating artificial neural network with Markov chain-cellular automata[J]. International Journal of Geographical Information Science, 2019, 33(10): 1960-1983. DOI:10.1080/13658816.2019.1600701 |
| [9] |
ZENG Haoran, ZHANG Bin, WANG Haijun. A hybrid modeling approach considering spatial heterogeneity and nonlinearity to discover the transition rules of urban cellular automata models[J/OL]. Environment and Planning B: Urban Analytics and City Science, 2023[2023-09-06]. https://DOI.org/10.1177/23998083221149018.
|
| [10] |
SHAFIZADEH-MOGHADAM H, ASGHARI A, TAYYEBI A, et al. Coupling machine learning, tree-based and statistical models with cellular automata to simulate urban growth[J]. Computers, Environment and Urban Systems, 2017, 64: 297-308. DOI:10.1016/j.compenvurbsys.2017.04.002 |
| [11] |
WANG Quan, WANG Haijun. An integrated approach of logistic-MCE-CA-Markov to predict the land use structure and their micro-spatial characteristics analysis in Wuhan metropolitan area, Central China[J]. Environmental Science and Pollution Research, 2022, 29(20): 30030-30053. DOI:10.1007/s11356-021-17750-6 |
| [12] |
WANG Haijun, ZHANG Bin, XIA Chang, et al. Using a maximum entropy model to optimize the stochastic component of urban cellular automata models[J]. International Journal of Geographical Information Science, 2020, 34(5): 924-946. DOI:10.1080/13658816.2019.1687898 |
| [13] |
张晓娟, 周启刚, 王兆林, 等. 基于MCE-CA-Markov的三峡库区土地利用演变模拟及预测[J]. 农业工程学报, 2017, 33(19): 268-277. ZHANG Xiaojuan, ZHOU Qigang, WANG Zhaolin, et al. Simulation and prediction of land use change in Three Gorges Reservoir Area based on MCE-CA-Markov[J]. Transactions of the Chinese Society of Agricultural Engineering, 2017, 33(19): 268-277. DOI:10.11975/j.issn.1002-6819.2017.19.035 |
| [14] |
HE Jialv, LI Xia, YAO Yao, et al. Mining transition rules of cellular automata for simulating urban expansion by using the deep learning techniques[J]. International Journal of Geographical Information Science, 2018, 32(10): 2076-2097. DOI:10.1080/13658816.2018.1480783 |
| [15] |
ZHAI Yaqian, YAO Yao, GUAN Qingfeng, et al. Simulating urban land use change by integrating a convolutional neural network with vector-based cellular automata[J]. International Journal of Geographical Information Science, 2020, 34(7): 1475-1499. DOI:10.1080/13658816.2020.1711915 |
| [16] |
谢志文, 王海军, 张彬, 等. 城市扩展元胞自动机多结构卷积神经网络模型[J]. 测绘学报, 2020, 49(3): 375-385. XIE Zhiwen, WANG Haijun, ZHANG Bin, et al. Urban expansion cellular automata model based on multi-structures convolutional neural networks[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(3): 375-385. DOI:10.11947/j.AGCS.2020.20190147 |
| [17] |
ZHANG Bin, WANG Haijun. A new type of dual-scale neighborhood based on vectorization for cellular automata models[J]. GIScience & Remote Sensing, 2021, 58(3): 386-404. |
| [18] |
LIU Jiamin, XIAO Bin, LI Yueshi, et al. Simulation of dynamic urban expansion under ecological constraints using a long short term memory network model and cellular automata[J]. Remote Sensing, 2021, 13(8): 1499. DOI:10.3390/rs13081499 |
| [19] |
SHI Xingjian, CHEN Zhourong, WANG Hao, et al. Convolutional LSTM network: a machine learning approach for precipitation nowcasting[EB/OL]. [2022-08-23]. https://arxiv.org/pdf/1506.04214.pdf.
|
| [20] |
FENG Yongjiu, WANG Rong, TONG Xiaohua, et al. How much can temporally stationary factors explain cellular automata-based simulations of past and future urban growth?[J]. Computers, Environment and Urban Systems, 2019, 76: 150-162. DOI:10.1016/j.compenvurbsys.2019.04.010 |
| [21] |
WANG Jiasheng, YANG Kun, ZHU Yanhui, et al. Euclidean distance transform on the sea based on cellular automata modeling[J]. Journal of Geodesy and Geoinformation Science, 2020, 3(2): 71-80. |
| [22] |
WEI Y D, LI Han, YUE Wenze. Urban land expansion and regional inequality in transitional China[J]. Landscape and Urban Planning, 2017, 163: 17-31. DOI:10.1016/j.landurbplan.2017.02.019 |
| [23] |
JI Shunping, ZHANG Chi, XU Anjian, et al. 3D convolutional neural networks for crop classification with multi-temporal remote sensing images[J]. Remote Sensing, 2018, 10(2): 75. DOI:10.3390/rs10010075 |
| [24] |
ELBOUSHAKI A, HANNANE R, AFDEL K, et al. MultiD-CNN: a multi-dimensional feature learning approach based on deep convolutional networks for gesture recognition in RGB-D image sequences[J]. Expert Systems with Applications, 2020, 139: 112829. DOI:10.1016/j.eswa.2019.112829 |
| [25] |
JI Shuiwang, XU Wei, YANG Ming, et al. 3D convolutional neural networks for human action recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(1): 221-231. DOI:10.1109/TPAMI.2012.59 |
| [26] |
KOCABAS V, DRAGICEVIC S. Assessing cellular automata model behaviour using a sensitivity analysis approach[J]. Computers, Environment and Urban Systems, 2006, 30(6): 921-953. DOI:10.1016/j.compenvurbsys.2006.01.001 |
| [27] |
PONTIUS R G, BOERSMA W, CASTELLA J C, et al. Comparing the input, output, and validation maps for several models of land change[J]. The Annals of Regional Science, 2008, 42(1): 11-37. DOI:10.1007/s00168-007-0138-2 |
| [28] |
SETO K C, FRAGKIAS M. Quantifying spatiotemporal patterns of urban land-use change in four cities of China with time series landscape metrics[J]. Landscape Ecology, 2005, 20(7): 871-888. DOI:10.1007/s10980-005-5238-8 |
| [29] |
CHEN Yimin, LI Xia, LIU Xiaoping, et al. Modeling urban land-use dynamics in a fast developing city using the modified logistic cellular automaton with a patch-based simulation strategy[J]. International Journal of Geographical Information Science, 2014, 28(2): 234-255. |
| [30] |
MCGARIGAL K. FRAGSTATS v4: spatial pattern analysis program for categorical and continuous maps[CP/OL]. [2022-08-23]. http://www.umass.edu/landeco/research/fragstats/fragstats.html.
|
| [31] |
CHEN Yimin, LI Xia, WANG Shujie, et al. Simulating urban form and energy consumption in the Pearl River Delta under different development strategies[J]. Annals of the Association of American Geographers, 2013, 103(6): 1567-1585. DOI:10.1080/00045608.2012.740360 |
| [32] |
MUDIGERE D, NAUMOV M, SPISAK J, et al. Building recommender systems with PyTorch[C]//Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York: ACM Press, 2020: 3525-3526.
|
| [33] |
KINGMA D P, BA J. Adam: a method for stochastic optimization[EB/OL]. [2022-08-23]. https://arxiv.org/abs/1412.6980.
|
| [34] |
JAMIN A, HUMEAU-HEURTIER A. Cross-entropy methods: a review[J]. Entropy, 2020, 22(1): 45. |
| [35] |
HINTON G E, SRIVASTAVA N, KRIZHEVSKY A, et al. Improving neural networks by preventing coadaptation of feature detectors[EB/OL]. [2022-08-23]. https://arxiv.org/abs/1207.0580
|



