城市场景的建筑物三维重建是当前计算机视觉、计算机图形学和摄影测量领域的一个重要研究内容,在城市规划[1]、可视化[2]、仿真模拟[3]、导航[4]、娱乐[5]等领域被广泛应用。传统的建筑物三维重建方法生成的网格模型准确详细,细节丰富且能够逼真地表示建筑物的几何结构特征,但稠密冗余的表示直接降低传输、处理以及渲染的性能,难以实时更新,不利于分析和应用,而高保真度、低复杂度的建筑物单体结构化模型具有更广泛的应用场景。
目前的建筑物单体结构化重建方法主要从实景三维数据中提取建筑物的平面结构、屋顶轮廓、立面轮廓、建筑物高度等几何信息,进而恢复建筑物的几何形状和拓扑结构。文献[6]通过随机采样一致(random sample consensus, RANSAC)算法[7]从点云中提取平面基元,将点云的三维空间划分为一组轴对齐盒子,通过对盒子进行筛选生成一个多边形表面模型来近似描述建筑物,效率低且不稳定。文献[8]在使用RANSAC算法[7]提取平面基元的基础上,通过平面基元的相交裁剪确定多边形表面模型的候选面,在基于马尔可夫随机场(Markov random field, MRF)的能量方程优化下剔除冗余面,生成一个紧凑简洁的封闭多边形表面模型。但由于平面相交生成了大量冗余面,只能处理复杂度较低的简单建筑物数据。为此文献[9]对平面基元进行自适应的空间划分,根据深度隐式场[10]计算其空间占有率,避免了冗余候选面的干扰。文献[11—12]也采用规则约束和连通性分析的方法,最大程度减少了冗余候选面的数量。文献[13]将室外场景的点云结构化重建拓展到了室内,但点云缺失依旧是重建的难题。网格相比点云在噪声和数据缺失方面都有很大的改善,文献[14]在先验知识和跨度约束下对网格以自适应变分方法[15]检测出地平面和立面轮廓,组合成一个完整且具有语义的多细节层次(level of details, LOD)模型[16]。对于大规模网格,文献[17]利用一个结合高度和图像特征的MRF图割[18-19],检测出屋顶轮廓和立面轮廓,进而生成LOD模型。在不考虑建筑物先验知识的情况下,文献[20]结合深度神经网络与网格几何约束,从网格和RGB图像、高度图、法向图中获得建筑物的清晰轮廓,灵活地对复杂的建筑物进行重建。但受限于网格轮廓几何特征的有限性,生成的LOD模型细节层次较低,而平面基元提取不仅可以获取更多的几何结构特征,还能利用拓扑结构。文献[21]采用区域生长算法提取网格的平面基元,根据面积阈值筛选出面积较大的平面基元进行多边形表面模型的构建,忽略了面积较小的平面基元,导致拓扑关系不准确,影响了重建的精度。文献[22]采用一环形邻域三角面区域生长的方法,极大地提高了平面基元提取的准确性,但同时重建了一些错误的几何结构,影响了多边形表面模型的整体精度。
为了解决当前方法存在的问题,本文提出了一种建筑物单体结构化重建的变尺度网格基元提取方法。本文工作有以下贡献:①提出了一种多尺度区域生长算法进行网格平面基元的提取,完整准确地提取出不同尺度大小的几何结构所对应的平面基元。②提出了一种平面基元拓扑优化算法,面积优先级策略有效提升了共面平面基元的合并效率。
1 单体结构化重建算法本文基于文献[21]提出的Polygonization方法,进行了多尺度区域生长提取网格平面基元、平面基元拓扑优化两个方面的改进,提出了一种有效且稳定的建筑物单体结构化重建的变尺度网格基元提取方法,重建出了更简洁紧凑的、结构化的多边形表面模型。本文的算法包括平面基元检测和多边形表面模型生成两个步骤,如图 1所示。Polygonization方法[21]采用单一尺度的平面基元提取方法,提取的平面基元不够完整和准确。为解决这一问题,本文提出多尺度区域生长算法和平面基元拓扑优化方法来提升平面基元提取的完整性和准确性。
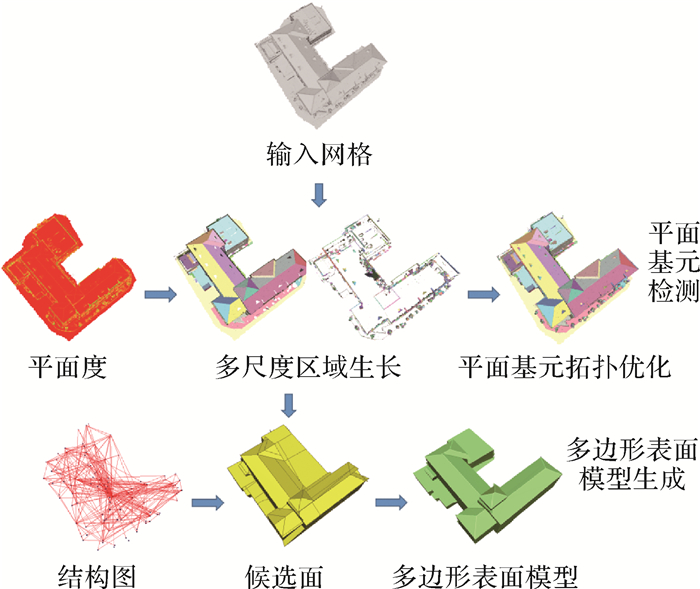
|
| 图 1 本文算法流程 Fig. 1 Flowchart of the proposed algorithm |
1.1 多尺度区域生长算法
平面基元的提取需要计算每个网格顶点的k-ring邻域平面度[23],如图 2所示,k-ring邻域描述了一个网格顶点的局部几何信息,因此可以通过一个网格顶点的k-ring邻域平面度描述其在k-ring邻域范围内平面的拟合质量[24]。计算出每一个网格顶点的平面度,三角面的平面度是其顶点平面度的平均值,将平面度最大的三角面作为区域生长的初始种子面。
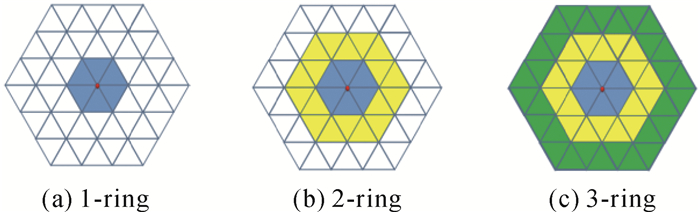
|
| 图 2 k-ring邻域图 Fig. 2 k-ring neighbourhood chart |
多尺度区域生长算法流程如图 3所示,首先通过检索初始种子面k-ring邻域三角面包含的网格顶点,拟合出初始参考平面,通过添加满足距离分割阈值和角度分割阈值的k-ring邻域三角面形成新的种子面,逐步向外扩张,重复整个过程直到将整个网格提取为若干平面基元,并标识不同的颜色进行可视化表示。
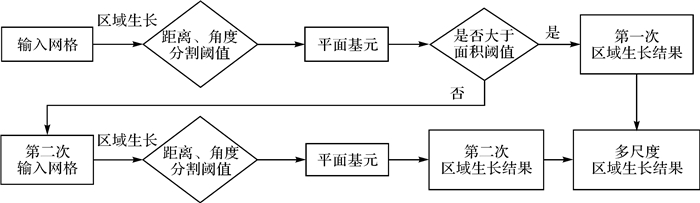
|
| 图 3 多尺度区域生长算法流程 Fig. 3 Flowchart of multi-scale region-growing algorithm |
由于初始网格表面的平坦性不足,存在大量的噪声和几何缺陷,因此需要适宜的距离分割阈值和角度分割阈值保证区域生长的准确性。
距离分割阈值是多尺度区域生长算法准确提取网格平面基元的关键,通过衡量种子面的k-ring邻域三角面到参考平面的投影距离进行平面基元的提取。如果投影距离大于距离分割阈值,判定该三角面不属于当前平面基元。通常情况下,网格的平均边长是距离分割阈值一个很好的参考数值,但对于所有建筑物网格模型而言,并非总能取得最优的平面基元提取结果。因此根据网格三角面的尺度规模大小,按照式(1)构建距离分割阈值,以平均边长作为基本参考数值,通过调整系数控制距离分割阈值的大小
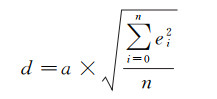 (1)
(1)
式中,ei是三角面的边长;n是三角面边的数量;a是调整系数,本文通常情况下a设定为1。
角度分割阈值通过衡量种子面的k-ring邻域三角面与参考平面的法向夹角进行平面基元的提取,如果夹角大于角度分割阈值,判定该三角面不属于当前平面基元。一个适宜的角度分割阈值在多尺度区域生长过程中既能保证降低网格表面噪声对平面基元提取的影响,又能准确地识别出平面基元的边界,角度分割阈值按照式(2)进行构建
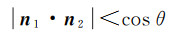 (2)
(2)
式中,n1和n2分别是参考平面和三角面经过归一化后的法向量;θ是角度阈值,由于建筑物网格模型表面并不平坦,因此本文角度分割阈值通常情况下设定为30°。
第一次区域生长采用的距离分割阈值难以提取尺度较小的平面基元。为此,本文首先设定适宜的面积阈值将尺度较大的平面基元筛选出来,对尺度较小的几何结构所对应的平面基元进行第二次区域生长。第二次区域生长的距离分割阈值由剩余的三角面边长重新计算,而角度分割阈值不变。
面积阈值的确定采用最大类间方差法(OSTU)[25]图像灰度分割算法的原理,将平面基元的面积值分成一大一小两类,保证类间方差最大化,有效地对平面基元进行筛选。首先将平面基元按照面积值从大到小进行排序,令{S1, S2, S3, …, SN}表示排序后N个平面基元的面积值,假设选择一个阈值Sk(SN < Sk < S1),将平面基元分为C1和C2两类,其中C1由面积值在[Sk, S1]内的平面基元组成,C2由面积值在[SN, Sk)内的平面基元组成。则平面基元被分类到C1的概率为P1,被分类到C2的概率为P2,C1类的平面基元的面积平均值为m1,C2类的平面基元的面积平均值为m2,所有平面基元的面积平均值为m,则类间方差可定义为
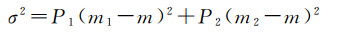 (3)
(3)
即m1和m2两个均值隔得越远,σ2越大,两个部分的差异性越大,越能有效地将平面基元按照面积值分成两部分。
如图 4所示,多尺度区域生长算法采用不同大小的距离分割阈值分两次从网格中提取平面基元,有效解决了单一尺度区域生长算法提取网格平面基元不准确、不规则的问题,更完整准确地从网格不同尺度大小的几何结构中提取出对应的平面基元。
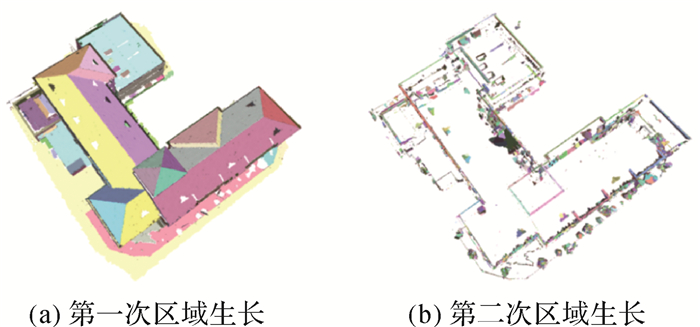
|
| 图 4 多尺度区域生长效果 Fig. 4 Effect of multi-scale region-growing |
1.2 平面基元拓扑优化
平面基元拓扑优化包括两个内容:合并共面的平面基元及恢复平面基元的邻接关系。Polygonization方法[21]穷举所有的平面进行合并,计算复杂度高。而本文采用面积优先级策略(图 5),减少平面基元的遍历次数,提高合并的效率。具体如下:①首先计算平面基元的面积,按照面积从大到小进行优先级排序;②选择面积最大的平面基元作为初始平面基元,按照优先级逐一去遍历其他平面基元,计算两个平面基元之间的投影距离和法向夹角,将满足距离阈值(参照式(1))和角度阈值(设为10°)的平面基元与初始平面基元进行合并;③未满足合并条件的平面基元重新筛选出优先级最高的作为初始平面基元,继续按照优先级执行合并;直到完成所有共面平面基元的合并。

|
| 图 5 合并共面的平面基元 Fig. 5 Merging co-planar planar primitives |
平面基元之间的邻接关系需要依靠三角面来确定,具体过程如图 6所示。只要两个平面基元之间存在至少一个公共的网格顶点,就认为它们是相邻的。恢复平面基元之间的邻接关系,保证拓扑完整准确,这对后续确定建筑物的轮廓至关重要。
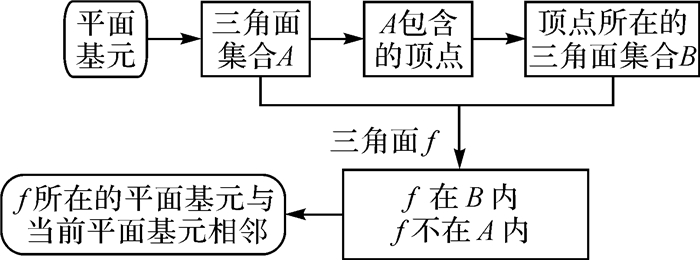
|
| 图 6 恢复平面基元的邻接关系 Fig. 6 Restoring the adjacency of planar primitives |
1.3 多边形表面模型生成
如图 7所示,根据平面基元之间的邻接关系,本文构建一个结构图来存储平面基元。结构图中的每一个顶点对应于一个平面基元,而如果两个顶点对应的平面基元相邻,则用一条边进行相连。为了更加准确有效地生成候选面,将结构图中的平面基元拟合成平面,通过平面的相交裁剪确定建筑物的轮廓,进而生成候选面。最终通过MRF的能量方程优化从候选面中筛选出一组最优的平面生成水密流形的多边形表面模型。
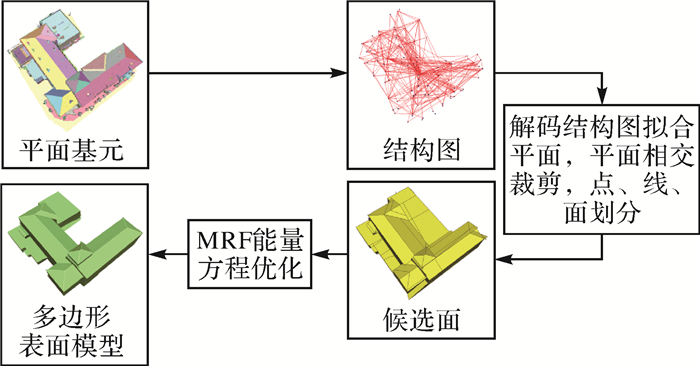
|
| 图 7 多边形表面模型生成 Fig. 7 Generation of polygonal surface model |
2 试验结果与分析
为了验证本文建筑物单体结构化重建的变尺度网格基元提取方法的有效性,在Windows10操作系统下,采用计算机硬件配置如下:3.20 GHz Intel Core i7-8700 CPU、64 GB RAM,使用C+ +实现了本文的方法,并对一组城市场景的建筑物网格模型进行了试验。
2.1 试验结果试验结果如图 8所示,第一列输入的原始网格是通过文献[26]的方法创建的单个非封闭建筑物网格,网格的复杂程度从网格a—网格f逐渐递增,噪声也随之递增。第二列是采用二次度量误差(quadic error metrics, QEM)[27]网格简化算法进行简化的效果,第三列是采用Polygonization方法[21]生成的多边形表面模型,第四列是本文方法生成的多边形表面模型。

|
| 图 8 试验结果 Fig. 8 Experimental results |
QEM算法对于噪声较少且比较简单的网格a和网格b,简化效果还比较规则准确;但面对复杂且噪声较多的网格c—f,简化后的网格表面凹凸不平,轮廓边界很不规则,甚至出现了变形。采用Polygonization方法能够较为规则准确地重建出尺度较大的建筑物主体结构,但对于尺度较小且复杂的几何结构,极易重建错误甚至无法重建。而本文方法有效地改善了这一情况,从网格a—f,不仅规则准确地重建出了尺度较大的建筑物主体结构,尺度较小且复杂的几何结构也能够重建出来,具备了更丰富的结构特征。
计算Hausdorff距离[28]评估多边形表面模型与原始网格的近似程度即模型精确度,如表 1所示。表 1中蓝色表示多边形表面模型与原始网格之间误差较小,红色则表示误差较大。可以发现,相比Polygonization方法[21],本文重建出的多边形表面模型与原始网格之间存在较小的误差,RMSE值更小,具备更高的精确度,较为准确地恢复了建筑物的几何结构,且具备较强的噪声抗干扰能力。
| 网格 | Polygonization方法 | RMSE | 本文方法 | RMSE |
| a |  |
4.04 |  |
3.58 |
| b |  |
4.09 |  |
3.90 |
| c |  |
0.65 |  |
0.53 |
| d |  |
1.22 |  |
1.10 |
| e |  |
1.92 |  |
1.42 |
| f |  |
2.30 |  |
2.02 |
图 9通过比较每一阶段的时间成本进行重建效率的对比。由于多尺度区域生长算法提取到数量更多的平面基元,因此时间成本略高;但通过本文的平面基元拓扑优化,更多的平面基元却耗费了更短的时间,更高效地完成了平面基元的拓扑优化,效率提升明显;由于生成的平面较多,在模型生成阶段耗费了较多的时间进行筛选,但总时长相比Polygonization方法仍有明显的优势。

|
| 图 9 模型的重建效率比较 Fig. 9 Comparison of the reconstruction efficiency of the models |
多边形表面模型的三角面数量如表 2所示,本文方法最大程度地实现了数据量的压缩,相比网格而言,更加轻量化,简化率低于0.5%,仍能够准确规则地描述建筑物的几何结构。虽然三角面数量比Polygonization方法略高一点,这是由于本文方法生成的模型保留了尺度较小的几何结构,细节方面更加丰富。
| 网格 | 原始 | Polygonization | 本文方法 |
| a | 243 371 | 126 | 348 |
| b | 160 052 | 130 | 368 |
| c | 195 032 | 172 | 336 |
| d | 176 312 | 176 | 381 |
| e | 182 488 | 126 | 458 |
| f | 301 998 | 378 | 803 |
2.2 多尺度区域生长的影响 2.2.1 k-ring邻域选择
本文对k-ring邻域在平面基元提取过程中的影响进行了定性分析(表 3)。如表 3所示,1-ring和2-ring邻域由于包含数量较少的网格顶点,局部平面拟合过程缺乏强有力的约束条件,对噪声过于敏感,因此平面基元的边界不能清晰完整地检测出来,导致平面基元提取错误,RMSE值较大,降低了多边形表面模型的重建精度。相对来说3-ring和4-ring邻域的局部平面拟合质量较高,能够准确地检测出平面基元的边界,可靠地引导多尺度区域生长算法进行平面基元的提取,RMSE值较小,重建的多边形表面模型更加精确;但4-ring邻域相比3-ring邻域效果上并没有很大的提升,效率上却降低了很多,因此本文试验均采用3-ring邻域。
| k-ring | 平面度 | 区域生长耗时/s | RMSE/m |
| 1-ring |  |
15.04 | 2.49 |
| 2-ring |  |
24.89 | 2.35 |
| 3-ring |  |
31.38 | 2.02 |
| 4-ring |  |
55.86 | 2.01 |
2.2.2 多尺度区域生长的影响
为了突出体现多尺度区域生长算法的有效性,本文进行了多尺度与单一尺度区域生长算法的对比试验(图 10)。通过图 10可以发现单一尺度区域生长算法由于将噪声和几何缺陷也提取到平面基元中,导致提取的平面基元并不准确规则,建筑物尺度较小的几何结构损失严重,直接降低了多边形表面模型的重建精度,甚至会导致重建失败。相比之下,多尺度区域生长算法降低了噪声和几何缺陷的影响,能够准确完整地提取出女儿墙、烟囱、多层屋顶、配电箱等尺度较小的几何结构所对应的平面基元,平面基元的边界处也更加准确规则,损失了较少的几何结构特征,能够更稳健地对建筑物网格模型进行平面基元的提取。
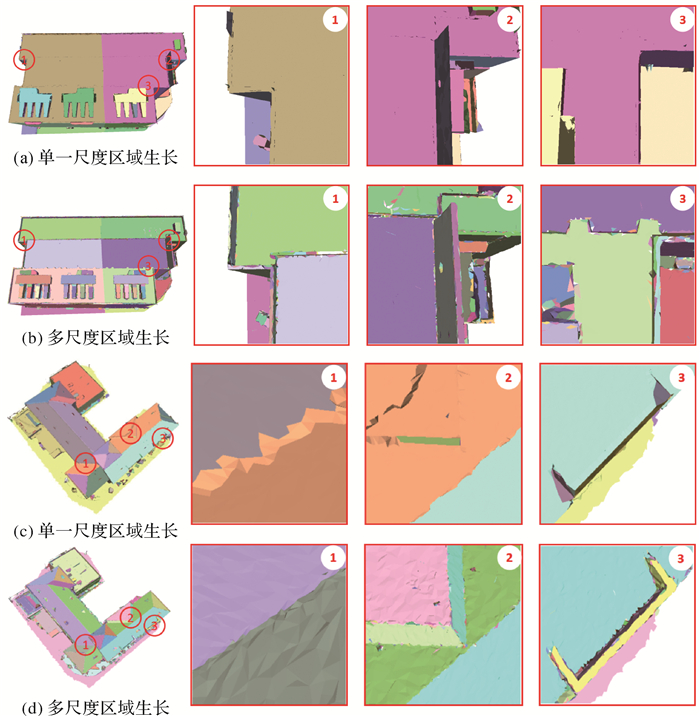
|
| 图 10 多尺度区域生长的影响 Fig. 10 Influence of multi-scale region-growing |
2.3 平面基元拓扑优化的影响
平面基元拓扑优化过程中,本文通过面积优先级策略合并共面的平面基元,减少平面基元的遍历次数,有效提高了合并效率。为了更直观地突出面积优先级策略的效率提升,本文进行了的对比试验。由于合并效率和平面基元的数量有关,因此试验采用的网格具备不同数量的平面基元,试验结果如图 11所示。通过图 11可以发现,面积优先级策略相比穷举方法,计算复杂度低,合并效率明显提升,在本文试验所用的网格上提高了5~10倍。
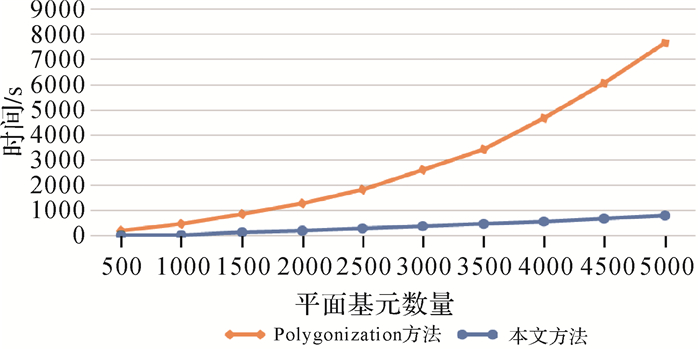
|
| 图 11 合并共面平面基元的效率对比 Fig. 11 Comparison of the efficiency of merging co-planar primitives |
2.4 限制因素
本文方法依赖平面基元提取的准确性和完整性。如图 12所示,由于网格的分辨率有限,一些几何结构只由几个三角面组成,在几何结构极其复杂或过于平滑的区域,平面基元的提取并不准确;而且网格表面曲率逐渐变化的弧形结构也很难准确地用平面去近似表示,因此就会丢失几何结构特征,影响重建的精度。在平面基元拓扑优化方面,本文采用的面积优先级策略虽然提高了效率,但并没有采用多线程等高性能计算技术,如果网格的几何结构过于复杂,效率并不突出。

|
| 图 12 不准确的平面基元 Fig. 12 Inaccurate planar primitives |
3 结论
本文提出了一种建筑物单体结构化重建的变尺度网格基元提取方法,生成的多边形表面模型在精确度和细节层次方面有了一定程度上的提升。多尺度区域生长算法有效解决了单一尺度区域生长算法提取平面基元不准确、边界不规则的问题,能够完整准确地从网格不同尺度的几何结构中提取出平面基元,降低了结构特征的损失,增强了噪声的抗干扰能力;并通过平面基元拓扑优化进一步改善平面基元的质量,其中面积优先级策略有效地提高了共面平面基元5~10倍的合并效率。但本文的方法仍有一些亟待改进之处,后续工作会进一步优化现有的算法,实现高效率高精度的建筑物单体结构化重建。
| [1] |
HERBERT G, CHEN Xuwei. A comparison of usefulness of 2D and 3D representations of urban planning[J]. Cartography and Geographic Information Science, 2015, 42(1): 22-32. DOI:10.1080/15230406.2014.987694 |
| [2] |
YAO Zhihang, NAGEL C, KUNDE F, et al. 3DcityDB: a 3D geodatabase solution for the management, analysis, and visualization of semantic 3D city models based on CityGML[J]. Open Geospatial Data, Software and Standards, 2018, 3(1): 1-26. DOI:10.1186/s40965-018-0043-x |
| [3] |
STOTER J, PETERS R, COMMANDEUR T, et al. Automated reconstruction of 3D input data for noise simulation[J]. Computers, Environment and Urban Systems, 2020, 80: 101424. DOI:10.1016/j.compenvurbsys.2019.101424 |
| [4] |
CAPPELLE C, EL NAJJAR M E, CHARPILLET F, et al. Virtual 3D city model for navigation in urban areas[J]. Journal of Intelligent and Robotic Systems, 2012, 66(3): 377-399. DOI:10.1007/s10846-011-9594-0 |
| [5] |
KARGAS A, LOUMOS G, VAROUTAS D. Using different ways of 3D reconstruction of historical cities for gaming purposes: the case study of Nafplio[J]. Heritage, 2019, 2(3): 1799-1811. DOI:10.3390/heritage2030110 |
| [6] |
LI Minglei, WONKA P, NAN Liangliang. Manhattan-world urban reconstruction from point clouds[C]//Proceedings of 2016 European Conference on Computer Vision. Cham: Springer, 2016: 54-69.
|
| [7] |
SCHNABEL R, WAHL R, KLEIN R. Efficient RANSAC for point-cloud shape detection[J]. Computer Graphics Forum, 2007, 26(2): 214-226. DOI:10.1111/j.1467-8659.2007.01016.x |
| [8] |
NAN L L, WONKA P. PolyFit: polygonal surface reconstruction from point clouds[C]// Proceedings of 2017 IEEE International Conference on Computer Vision. Venice: IEEE, 2017: 2372-2380.
|
| [9] |
CHEN Z, LEDOUX H, KHADEMI S, et al. Reconstructing compact building models from point clouds using deep implicit fields[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2022, 194: 58-73. DOI:10.1016/j.isprsjprs.2022.09.017 |
| [10] |
ERLER P, GUERRERO P, OHRHALLINGER S, et al. Points2Surf: learning implicit surfaces from point clouds[EB/OL]. [2022-06-28]. https://arxiv.org/pdf/2007.10453.pdf.
|
| [11] |
XIE Linfu, HU Han, ZHU Qing, et al. Combined rule-based and hypothesis-based method for building model reconstruction from photogrammetric point clouds[J]. Remote Sensing, 2021, 13(6): 1107. DOI:10.3390/rs13061107 |
| [12] |
FANG H, LAFARGE F. Connect-and-slice: an hybrid approach for reconstructing 3D objects[C]// Proceedings of 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020: 13487-13495.
|
| [13] |
崔扬. 移动LiDAR点云室内三维结构化重建方法和关键技术研究[J]. 测绘学报, 2021, 50(7): 990. CUI Yang. Research on methodology and the key technology of indoor 3D structured reconstruction from mobile LiDAR point clouds[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(7): 990. DOI:10.11947/j.AGCS.2021.20200592 |
| [14] |
ZHU Lingjie, SHEN Shuhan, HU Lihua, et al. Variational building modeling from urban MVS meshes[C]//Proceedings of 2017 International Conference on 3D Vision. Qingdao: IEEE, 2018: 318-326.
|
| [15] |
COHEN-STEINER D, ALLIEZ P, DESBRUN M. Variational shape approximation[J]. ACM Transactions on Graphics, 23(3): 905-914.
|
| [16] |
CityGML. CityGML[EB/OL]. [2023-06-28]. http://www.opengeospatial.org/standards/citygml.
|
| [17] |
ZHU Lingjie, SHEN Shuhan, GAO Xiang, et al. Large scale urban scene modeling from MVS meshes[C]//Proceedings of the 15th European Conference. Munich: Springer, 2018: 640-655.
|
| [18] |
BOYKOV Y, KOLMOGOROV V. An experimental comparison of min-cut/max- flow algorithms for energy minimization in vision[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(9): 1124-1137. DOI:10.1109/TPAMI.2004.60 |
| [19] |
BOYKOV Y, VEKSLER O, ZABIH R. Fast approximate energy minimization via graph cuts[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2001, 23(11): 1222-1239. DOI:10.1109/34.969114 |
| [20] |
ZHU Lingjie, SHEN Shuhan, GAO Xiang, et al. Urban scene vectorized modeling based on contour deformation[J]. ISPRS International Journal of Geo-Information, 2020, 9(3): 162. DOI:10.3390/ijgi9030162 |
| [21] |
BOUZAS V, LEDOUX H, NAN L. Structure-aware building mesh polygonization[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2020, 167: 432-442. DOI:10.1016/j.isprsjprs.2020.07.010 |
| [22] |
YAN Li, LI Yao, XIE Hong. Urban building mesh polygonization based on 1-ring patch and topology optimization[J]. Remote Sensing, 2021, 13(23): 4777. DOI:10.3390/rs13234777 |
| [23] |
GATZKE T D, GRIMM C M. Estimating curvature on triangular meshes[J]. International Journal of Shape Modeling, 2006, 12(1): 1-28. DOI:10.1142/S0218654306000810 |
| [24] |
PAULY M, GROSS M, KOBBELT L P. Efficient simplification of point-sampled surfaces[C]//Proceedings of 2002 IEEE Visualization. Boston: IEEE, 2022: 163-170.
|
| [25] |
OTSU N. A threshold selection method from gray-level histograms[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1979, 9(1): 62-66. DOI:10.1109/TSMC.1979.4310076 |
| [26] |
邓非, 颜青松, 肖腾. 多视密集匹配并行传播GPU-PatchMatch算法[J]. 测绘学报, 2020, 49(2): 181-190. DENG Fei, YAN Qingsong, XIAO Teng. A GPU-PatchMatch multi-view dense matching algorithm based on parallel propagation[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(2): 181-190. DOI:10.11947/j.AGCS.2020.20180459 |
| [27] |
GARLAND M, HECKBERT P S. Surface simplification using quadric error metrics[C]//Proceedings of the 24th Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM Press, 1997: 209-216.
|
| [28] |
GUTHE M, BORODIN P, KLEIN R. Fast and accurate Hausdorff distance calculation between meshes[EB/OL]. [2022-06-28]. http://wscg.zcu.cz/wscg2005/Papers_2005/Full/F61-full.pdf.
|



