2. 中国地震局中国地震台网中心, 北京 100045;
3. 中国气象局气象探测中心, 北京 100081
2. China Earthquake Networks Center, China Earthquake Administration, Beijing 100045, China;
3. Meteorological Observation Center of China Meteorological Administration, Beijing 100081, China
随着地球气候以前所未有的速度变暖,全球范围内降水和蒸散的规模、频率、时间和类型正发生着变化[1-4]。预计这些变化将进一步加剧,影响到全球水文循环,因此监测水资源变化变得更加重要。近年来,GNSS作为一种新的监测陆地水储量(terrestrial water storage, TWS)的大地测量技术[1-2, 4]应运而生,由此诞生了GNSS水文学这个交叉学科。GNSS监测TWS原理与GRACE(gravity recovery and climate experiment) 有所不同,GRACE卫星重力观测能直接感应TWS(质量)变化,而GNSS地壳垂直位移(vertical crustal displacements, VCD)记录了由于海平面变化、大气环流、冰川和冰盖演变、雪和降雨以及河流、湖泊、土壤和地下水含水层储水变化等不同表面荷载作用下地球表面变形而引起的地球表面微小但可测量的荷载引起的位移[5-6]。相比GRACE的天基技术,地基观测的GNSS可借助持续发展、通用性强的连续运行参考站网系统(continuously operating reference system, CORS)(例如美国西部板块边界观测实验室(Plate Boundary Observatory, PBO)、日本地球观测网络(GPS Earth Observation Net work of Japan, GEONET)、欧洲EPN(European Permanent Network)等),无须高额投入。研究表明,GNSS监测TWS与GRACE结果具有广泛的一致性[7]。密集的GNSS台网可以得到更高时空分辨率的TWS变化图像。例如PBO可将美国西部地区TWS空间分辨率提升至50 km[1-2],利用GNSS技术得出的洛基山脉及太平洋西海岸TWS分布状况图像可清楚显示俄勒冈和华盛顿州的季节性降水集中于Cascade和Olympic山区,而相邻的Columbia和Harney盆地降水不多,盆山地形过渡带明显对应了一条干湿分界线,与气象观测十分接近[3]。相反,该地区GRACE图像很难分辨以上细微特征[7]。在四川地区开展的TWS研究也得出类似结论, GNSS图像揭示出TWS分布在成都平原、川西高原及川南地区间的显著差异,山区TWS展示出更大的季节性变化,尤其受西南印度季风控制的季节性降水导致川南一带TWS的大幅变动[8-11]。以上研究结果表明,GRACE能够量化300 km范围内(空间尺度)的TWS每月(时间尺度)变化,而GNSS能反映具有更高空间分辨率(50 km)和时间分辨率(1 d,甚至数小时)的TWS精细变化,与GRACE得到的总体结果形成互补。
目前,GNSS反演TWS主要有格林函数[5, 8, 11]和Slepian基函数[10, 12-13]两种方法;基于Farrell[6]的空间域卷积格林函数方法可用于确定50~100 km分辨率的陆地水存储变化,明显优于GRACE提供的分辨率;当研究区域相对较小(区域、省份)且GNSS测站覆盖足够密集时,格林函数反演方法较合适。当研究范围较大(国家、大洲)、GNSS网络的空间覆盖不太密集时,格林函数方法则受到限制[14];Slepian基函数方法类似于GRACE的大范围尺度的反演技术[15]。GRACE重力数据通常使用球面谐波(SH)基函数(整个球面内正交)进行分析,而陆地范围只占整个球面29.2%,基于局部SH基函数或球面Slepian基函数对GNSS数据进行参数化和反演TWS,以获得区域(而非全球)表面质量变化。
理论上,格林函数与球谐函数在数学模型上是等价的[16],而在实际应用上却存在差异。目前,众多学者研究GNSS数据反演陆地水储量均采用单一方法,但是在同一地区不同方法的反演结果究竟存在多大差异,尚缺少定量分析。因此,本文在同一研究区域,使用相同数据,分别采用上述两种方法反演GNSS等效水高(equivalent water height,EWH),并进行结果对比研究,定量分析格林函数和Slepian基函数反演方法的差异。
本文研究区域选择在云南地区(97°E—107°E、20°N—30°N),首先介绍格林函数和Slepian基函数反演陆地水的方法和数学模型,然后基于模拟数据与真实GNSS连续观测站坐标时间序列详细对比分析格林函数和Slepian基函数反演效果,同时与GRACE球谐系数产品、GLDAS水文模型和降水数据进行了相关性分析。本文的研究结果可以为近实时观测的GNSS在流域尺度研究水文荷载提供参考。
1 原理与方法 1.1 格林函数格林函数(Green's function)是一个数学物理方程[6, 17],它表示一种特定的“场”和产生这种场的“源”之间的关系。对地球物理大地测量领域里的反演而言,线性反演的首要工作是建立线性的函数模型(线性观测方程组)[18]。在GNSS水文研究中,格林函数为地表水单位负荷对GNSS观测点的形变贡献量。线性反演的数学模型表述如下[2, 17, 19]
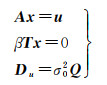 (1)
(1)
式中,A为格林函数;x为待估参数向量(等效水高);u为观测值(GNSS位移场);β为参数列向量的平滑因子;T为参数向量的平滑约束矩阵(如Laplace拉普拉斯二阶差分平滑算子);Du为观测列向量的方差-协方差矩阵;σ02为单位权中误差;Q为观测列向量的协因数矩阵。
根据Tikhonov正则化原理,建立GNSS反演陆地水储量估计准则[5, 8, 20-22]
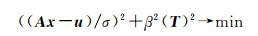 (2)
(2)
格林函数反演结果受GNSS测站数量和空间分布影响程度大,研究区域较大时,划定的格网面积过大会导致反演效果不佳,因此在大尺度陆地水储量的反演研究还是采用GRACE技术为主。然而如前所述,球谐函数在全球范围内满足正交性,在局部研究区域内会存在“泄漏”,球面Slepian基函数可以最大限度地减少信号从研究区域“泄漏”[14]。因此,研究者开始研究使用Slepian基函数反演GRACE和GNSS数据以获得大尺度等效水高[12-14]。
本文研究区域内表面水质量载荷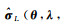
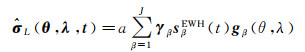 (3)
(3)
式中,a为地球半径;J为截断阶数;γβ为特征值(也称为聚集因子);sβEWH为Slepian基函数系数;gβ(θ, λ)为Slepian基函数。
1.3 数据和处理策略定量对比研究GNSS两种反演EWH方法,本文收集了两类实测空间大地测量数据进行反演计算。
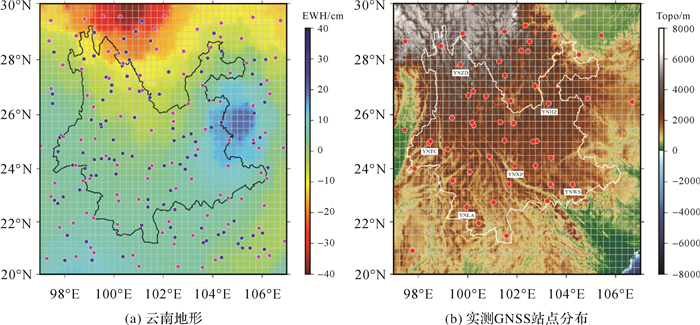
(1) 使用美国CSR(Center for Space Research) 提供的GRACE/GRACE-FO RL06 Mascon数据(图 1(a)),并使用计算机随机函数rand()在整个研究区域内随机生成100个点位作为随机分布GNSS模拟站(图 1(a)蓝色)和将1600个格网平均分成100个4×4的区域,每个区域内随机生成1个点位(共100点)作为平均分布GNSS模拟站(图 1(a)洋红色);
|
| 图 1 CSR提供的GRACE-Mascon等效水高以及模拟GNSS测站(洋红表示平均分布、蓝色表示随机分布) Fig. 1 GRACE-Mascon equivalent water height provided by CSR and simulated GNSS stations (magenta indicates average distribution and blue indicates random distribution) |
(2) 采用中国大陆构造环境监测网络简称“陆态网络”(Crustal Motion Observation Network of China, CMONOC)和中国气象局(China Meteorological Administration, CMA)建设的54个GNSS连续观测站(图 1(b)),由图 1(b)地形中清晰看到,云南地区西北海拔高(最大海拔7600 m),东南海拔低(最低海拔仅76 m),呈现明显的西北-东南的海拔降低梯度。云南全省25°坡度以下区域占比56.46%,文献[27]研究表明,显著的地形坡度会影响GNSS反演陆地水的结果,忽略地形改正使得GNSS反演陆地水的振幅偏大。
GNSS日解坐标时间序列数据来源于中国地震数据中心(China Earthquake Data Center,CEDC, http://www.eqdsc.com/)和中国气象局。为了更好地反映真正的地表垂直弹性变形,需要对GNSS位置时间序列中的非水文负载信号进行识别和剔除,本文采用德国地学中心(Geo Forschungs Zentrum, GFZ) 的地球系统建模小组(Earth System Modeling Group,ESM) 发布的地球物理流体荷载产品(http://esmdata.gfz-potsdam.de:8080/repository)去除GNSS时间序列数据包含的固体地球表面几何中心框架(CF)中非潮汐海洋和大气荷载位移;冰后回弹效应导致中国各地地壳抬升0.3~0.6 mm/a[11],本文使用ICE-6G_D模型进行校正[11]。GNSS数据经过原始数据解算和后处理改正后得到主要包含由陆地水文变化造成的地表位移波动序列。
对于每个GNSS时间序列 u(t),采用截距b,速率v和余弦、正弦表示的周年和半周年的季节性项的线性模型
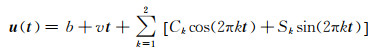 (4)
(4)
式中,时间 t以年为单位;周年项的振幅Amp和相位day(最大值出现在一年中的第几天)计算方法为
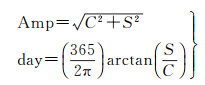 (5)
(5)
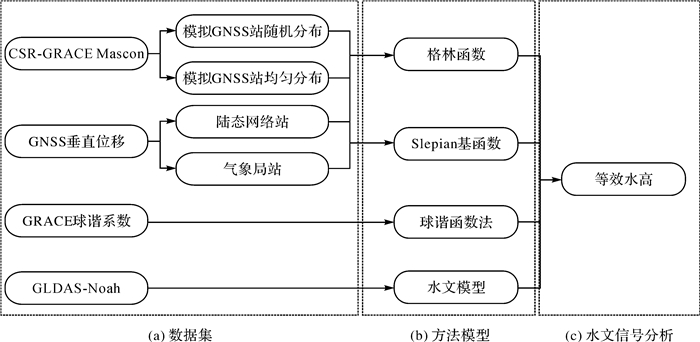
本文数据处理策略如图 2。
|
| 图 2 本文数据处理策略和流程 Fig. 2 Data processing strategy and process |
(1) 图 2(a)数据集:①利用CSR提供的GRACE Mascons格网数据,在研究区域内,按照随机方式和平均方式各生成100个GNSS测站;②实测GNSS连续站数据;③GRACE球谐系数;④GLDAS-Noah产品。
(2) 图 2(b)方法模型:①模拟数据采用格林函数方法和Slepian基函数方法反演等效水高;②实测GNSS连续站数据分别采用两种反演方法计算等效水高;③GRACE球谐函数法;④GLDAS-Noah水文模型。
(3) 图 2(c)水文信号分析:①GNSS反演的等效水高和GRACE Mascons格网数据进行定量对比分析;②定量比较两种反演方法计算的等效水高时间序列(振幅、相位);③将GNSS反演结果和GRACE球谐函数法及GLDAS-Noah水文模型进行对比。
2 结果与分析本文采用棋盘测试[8]来评估格林函数反演结果,图 3显示了3种GNSS分布策略的棋盘测试结果(β=0.01);由图 3可以清晰地看出,测站分布越均匀(图 3(b)和(c)对比)、测站数量越多(图 3(d)和(b)、(c)对比),反演效果越好。

|
| 图 3 棋盘测试评估格林函数反演结果 Fig. 3 Green's function inversion checkerboard test |
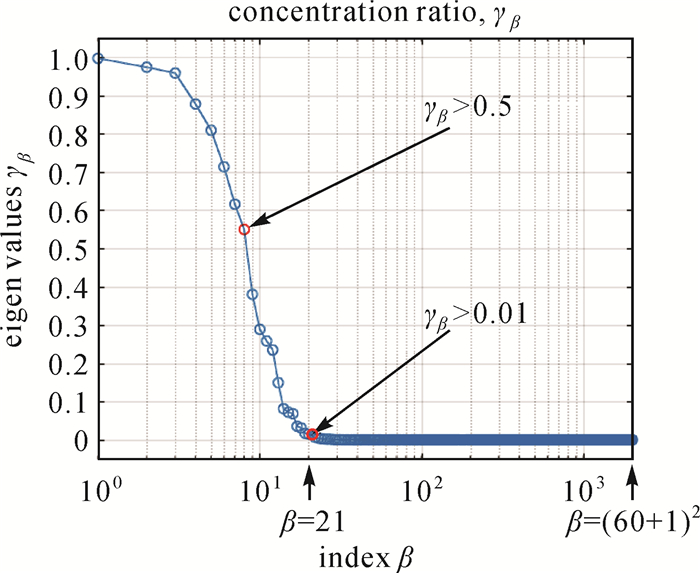
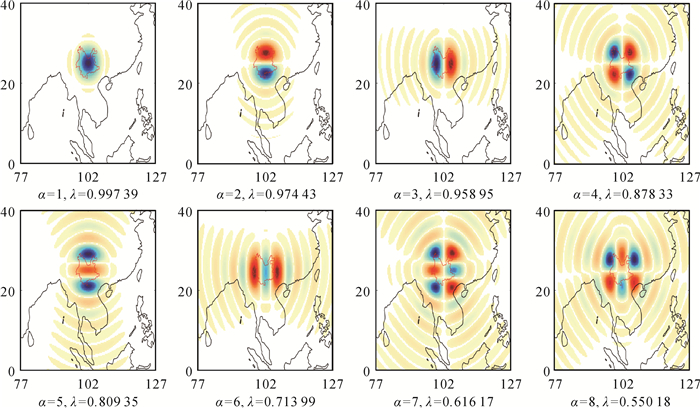
Slepian基函数空间分布呈现明显“空限”特征(图 4),本文展开到60阶,一共计算了(L+1)2= 3721个Slepian基函数,其中聚集度大于0.01阈值的共有21个基函数(图 5展示了前8个Slepian基函数空间分布),其贡献度达到99.74%,余下的3700个Slepian基函数,占总数的99.44%,其贡献度不足0.3%。
|
| 图 4 展开L=60阶,3721个Slepian基函数的聚集度 Fig. 4 Expanded L=60 order, the aggregation degree of 3721 Slepian basis functions |
|
| 图 5 前8个Slepian基函数的空间分布 Fig. 5 Spatial distribution of the top 8 Slepian basis functions |
基于模拟数据分析Slepian基函数,首先利用格林函数矩阵计算模拟的GNSS站点处的垂直位移,然后反演获得等效水高Slepian基函数系数 sβEWH。
基于GRACE Mascon的2015年1月“lwe_thickness”格网数据,从模拟随机分布的GNSS测站(图 1(a)、图 3(b)中的蓝色点)中选取其中的30、60、100个站点,利用格林函数和Slepian基函数分别进行等效水高EWH的反演。格林函数方法计算结果如图 6(a)—(c)所示,Slepian基函数计算结果如图 6(d)—(f)所示。

|
| 图 6 GNSS测站数不同格林函数((a)、(b)、(c))和Slepian基函数((d)、(e)、(f))反演结果差异 Fig. 6 Differences in inversion results of Green's function ((a)、(b)、(c)) and Slepian basis function ((d)、(e)、(f)) with different GNSS station numbers |
图 6每个子图右下角展示了不同GNSS测站数反演结果与图 1(a)所示的GRACE Mascons格网数据差值统计的直方分布,可直观反映反演结果的好坏。在研究区域内格林函数方法受测站数和站点空间分布影响较大(图 6(a)—(c)),如图 6所示,选取60个GNSS测站(图 6(b)),格林函数反演即可获得较好结果。从差值直方统计可以发现,Slepian基函数反演效果比格林函数反演结果略差;同时,Slepian基函数反演结果对测点空间分布差异和测站点数多寡敏感程度较弱。
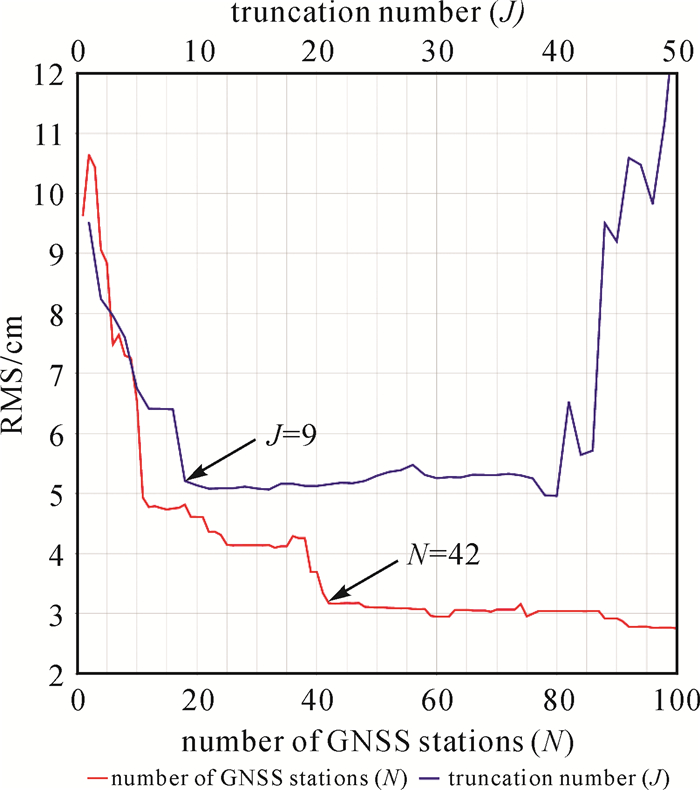
更进一步,定量分析GNSS测站数和Slepian基函数最大截断数对反演结果的影响。图 7红线为对应模拟随机选取不同测站数后反演结果RMS(root mean square)值的变化,多于42个测站后,RMS值变化相对平缓。图 7说明在研究区域,超过42个分布合理的GNSS测站能获得较为理想的反演结果。图 7蓝线为Slepian基函数选取不同截断数J反演结果RMS值,J=9时,可以获得最佳效果。
|
| 图 7 格林函数和Slepian基函数反演受GNSS测站数和最大截断数影响 Fig. 7 The inversion of Green's function and Slepian basis function is affected by the number of GNSS stations and the number of truncations |
基于上述试验结果,采用云南地区陆态网络和气象局实测的54个GNSS垂直位移数据,(时间跨度2010—2022年),进行GNSS水文研究。格林函数反演采用β=0.03,Slepian基函数与上面采用同样的展开阶数L=60和截断数J=9。在研究范围内不同区域(滇中、滇东南、滇东北、滇西、滇西南、滇西北)选取6个测站(图 1(b))反演的等效水高时间序列(图 8右侧);对比分析结果表明,格林函数和Slepian基函数反演的等效水高时间序列一致性非常高,统计所有测站两种方法结果的相关系数达到0.98(表 1)。GRACE球谐函数方法和GLDAS水文模型与GNSS反演的等效水高时间序列相关性均大于0.65,差异体现在GNSS反演的EWH空间分布更精细。同时,可以发现EWH时间序列波峰均出现在降雨量峰值之后,等效水高时间序列波动和降水数据(图 8 Preci)具有明显的一致性,波峰出现的时间比最大降雨滞后1~2个月,可能的原因是该地区地壳对荷载变化响应存在滞后,而且荷载变化被GNSS监测并在位移中体现出来需要时间。

|
| 图 8 GNSS垂直位移和反演EWH时间序列 Fig. 8 GNSS vertical displacement and inversion EWH time series |
| 方法 | GNSS_Green | GNSS_Slepian | GRACE_SHc | GLDAS_NOAH |
| GNSS_Green | - | - | - | - |
| GNSS_Slepian | 0.98 | - | - | - |
| GRACE_SHc | 0.77 | 0.79 | - | - |
| GLDAS_NOAH | 0.65 | 0.66 | 0.70 | - |
降雨数据表明,云南地区常年平均5月最为干燥,9月最为湿润。通过GNSS的2015年5月和2015年9月的垂直位移和反演等效水高(图 9)进一步分析发现,Slepian基函数反演结果(图 9(c)、(f))比格林函数反演结果(图 9(b)、(e)) 振幅略大,但两者空间分布趋势整体较为一致,相位几乎一致(图 8(b)、(d)、(f)、(h)、(j)、(l))。

|
| 图 9 GNSS垂直位移((a)、(d))、格林函数反演结果((b)、(e))、Slepian基函数反演结果((c)、(f)) Fig. 9 GNSS vertical displacement ((a), (d)), Green's function inversion results ((b), (e)), Slepian basis function inversion results ((c), (f)) |
统计研究区域内GNSS测站反演的结果表明,Slepian基函数反演的振幅比格林函数反演的振幅平均大25%(图 10、图 11)。笔者推测可能的原因是Slepian基函数反演GNSS等效水高,存在系统性偏差;GNSS站点的水文荷载导致的垂直位移,是周围半径50 km范围内[28]所有水文荷载贡献,而从Slepian基函数反演数学模型能看出,其将周围所有的水文荷载贡献都归集于GNSS站点处的水文荷载,这显然会导致Slepian基函数反演结果偏大;不同半径(范围)的水文荷载对GNSS站点垂直位移贡献程度除了与距离有关,还与荷载大小有关系。

|
| 图 10 3种不同的格网圆盘及地表荷载形变响应 Fig. 10 Three different grid disks, modeled vertical displacement under a disk load of radius 15.7 km and an equivalent water depth of 1 m |

|
| 图 11 GNSS垂直时间序列和反演等效水高时间序列 Fig. 11 Map of the GNSS vertical deformation timeseries and inversion EWH timeseries |
图 10显示,本文研究区域内采用0.25°×0.25°格网,每个格网边长约为28 km,3种不同的格网圆盘(图 10(a)内切圆半径14 km、图 10(b)外接圆半径19.8 km和图 10(c)等面积圆半径15.7 km);等面积圆能较好地代表每个格网的信息,本文采用格网等面积圆半径作为圆盘半径,图 10(d)为等效水高1 m、圆半径15.7 km的圆盘造成的地表形变响应,图 10(e)展示图 10(d)二维剖面,其中蓝色面积为±25 km2范围内荷载响应占整体比值0.705。
将Slepian基函数反演式(3)修改如下
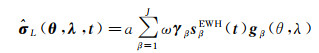 (6)
(6)
式中,ω表示Slepian反演方法“系统性偏差”改正参数,其根据荷载格林函数矩阵特性计算;若GNSS测站反映周围半径50 km范围内的陆地水荷载(空间分辨率50 km),根据格林函数矩阵可以获得不同格网圆盘半径的荷载-位移曲线,定义积分计算曲线在±25 km2以内的面积占整体面积的比值为参数ω,本文研究中ω=0.705。图 11显示了Slepian反演方法系统性偏差改正效果;ω参数改正前(图 11(c)、(e))后(图 11(d)、(e)),格林函数反演结果振幅与Slepian反演结果振幅相关性系数从0.48上升到0.88。
综合而言,在本文研究范围,实测的GNSS垂直时间序列反演等效水高,采用格林函数法和Slepian基函数法效果相当,两种方法均可用于该区域水文研究。另一方面,统计Slepian反演结果的振幅比格林函数反演结果的振幅平均大25%,Slepian反演方法存在系统性偏差,应根据荷载格林函数响应特性进行改正。基于Slepian反演GNSS陆地水在其他更大空间尺度区域上(空间分辨率>50 km)是否同样存在系统性偏差,将在未来研究中更详细验证与量化计算。
3 结语大地测量水文学研究通常探索水文荷载作用下地球变形与气候驱动因素之间的经验关系,以改善洪水和干旱等水文事件的预报。现如今,更高空间和时间分辨率的GNSS技术,能够研究近乎实时观测的流域尺度水文荷载。本文定量分析格林函数和Slepian基函数反演陆地水差异,在研究区域得到如下结论:①基于模拟数据,格林函数反演结果受GNSS测站数量和空间展布影响程度比Slepian基函数反演结果更大,而Slepian基函数反演结果受最大截断阶数的影响较大;同等情况下(GNSS测站数≥42),格林函数反演结果总体精度比Slepian基函数反演结果更优。②基于实测的“陆态网络”和中国气象局的GNSS连续测站垂直时间序列数据,两种方法反演等效水高结果相关性达到0.98,Slepian基函数反演结果振幅比格林函数反演结果振幅平均大25%。③GNSS数据反演的陆地水和GRACE、GLDAS推断的陆地水相关性均大于0.65,并且与该地区月度降水数据一致性很好;GNSS反演等效水高序列波峰出现的时间比最大降雨滞后1~2个月。
| [1] |
AMOS C B, AUDET P, HAMMOND W C, et al. Uplift and seismicity driven by groundwater depletion in central California[J]. Nature, 2014, 509(7501): 483-486. DOI:10.1038/nature13275 |
| [2] |
BORSA A A, AGNEW D C, CAYAN D R. Ongoing drought-induced uplift in the western United States[J]. Science, 2014, 345(6204): 1587-1590. DOI:10.1126/science.1260279 |
| [3] |
CHEW C C, SMALL E E. Terrestrial water storage response to the 2012 drought estimated from GPS vertical position anomalies[J]. Geophysical Research Letters, 2014, 41(17): 6145-6151. DOI:10.1002/2014GL061206 |
| [4] |
GALLOWAY D L, JONES D R, INGEBRITSEN S E. Land subsidence in the United States[M]. Restown: United States Geological Survey, 1999: 1182.
|
| [5] |
VAN DAM T, WAHR J, MILLY P C D, et al. Crustal displacements due to continental water loading[J]. Geophysical Research Letters, 2001, 28(4): 651-654. DOI:10.1029/2000GL012120 |
| [6] |
FARRELL W E. Deformation of the Earth by surface loads[J]. Reviews of Geophysics, 1972, 10(3): 761-797. DOI:10.1029/RG010i003p00761 |
| [7] |
BOCK Y, MELGAR D. Physical applications of GPS geodesy: a review[J]. Reports on Progress in Physics Physical Society (Great Britain), 2016, 79(10): 106801. |
| [8] |
FU Yuning, ARGUS D F, LANDERER F W. GPS as an independent measurement to estimate terrestrial water storage variations in Washington and Oregon[J]. Journal of Geophysical Research: Solid Earth, 2015, 120(1): 552-566. DOI:10.1002/2014JB011415 |
| [9] |
ZHONG Bo, LI Xianpao, CHEN Jianli, et al. Surface mass variations from GPS and GRACE/GFO: a case study in southwest China[J]. Remote Sensing, 2020, 12(11): 1835. DOI:10.3390/rs12111835 |
| [10] |
JIANG Zhongshan, HSU Y J, YUAN Linguo, et al. Characterizing spatiotemporal patterns of terrestrial water storage variations using GNSS vertical data in Sichuan, China[J]. Journal of Geophysical Research: Solid Earth, 2021, 126(12): e2021JB022398. DOI:10.1029/2021JB022398 |
| [11] |
何思源, 谷延超, 范东明, 等. 利用GPS垂直位移反演云南省陆地水储量变化[J]. 测绘学报, 2018, 47(3): 332-340. HE Siyuan, GU Yanchao, FAN Dongming, et al. Seasonal variation of terrestrial water storage in Yunnan province inferred from GPS vertical observations[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(3): 332-340. DOI:10.11947/j.AGCS.2018.20170255 |
| [12] |
成帅, 袁林果, 姜中山, 等. 应用GPS数据和Slepian基函数反演川云渝地区陆地水储量变化[J]. 地球物理学报, 2021, 64(4): 1167-1180. CHENG Shuai, YUAN Linguo, JIANG Zhongshan, et al. Investigating terrestrial water storage change in Sichuan, Yunnan and Chongqing using Slepian basis functions[J]. Chinese Journal of Geophysics, 2021, 64(4): 1167-1180. |
| [13] |
JIANG Zhongshan, HSU Y J, YUAN Linguo, et al. Estimation of daily hydrological mass changes using continuous GNSS measurements in mainland China[J]. Journal of Hydrology, 2021, 598: 126349. DOI:10.1016/j.jhydrol.2021.126349 |
| [14] |
HAN S C, RAZEGHI S M. GPS recovery of daily hydrologic and atmospheric mass variation: a methodology and results from the Australian continent[J]. Journal of Geophysical Research: Solid Earth, 2017, 122(11): 9328-9343. DOI:10.1002/2017JB014603 |
| [15] |
韩建成, 陈石, 卢红艳, 等. 基于Slepian方法和地面重力观测确定时变重力场模型: 以2011—2013年华北地区数据为例[J]. 地球物理学报, 2021, 64(5): 1542-1557. HAN Jiancheng, CHEN Shi, LU Hongyan, et al. Time-variable gravity field determination using Slepian functions and terrestrial measurements: a case study in North China with data from 2011 to 2013[J]. Chinese Journal of Geophysics, 2021, 64(5): 1542-1557. |
| [16] |
沈迎春, 闫昊明, 彭鹏, 等. 质量负荷引起地表形变的格林函数和球谐函数方法对比研究[J]. 武汉大学学报(信息科学版), 2017, 42(7): 1008-1014. SHEN Yingchun, YAN Haoming, PENG Peng, et al. Comparative study of Green's function and spherical harmonic function methods on surface deformation caused by mass loading[J]. Geomatics and Information Science of Wuhan University, 2017, 42(7): 1008-1014. |
| [17] |
孙和平. 大气重力格林函数[J]. 科学通报, 1997, 42(15): 1640-1646. SUN Heping. Green's function of atmospheric gravity[J]. Chinese Science Bulletin, 1997, 42(15): 1640-1646. DOI:10.3321/j.issn:0023-074X.1997.15.017 |
| [18] |
WAHR J, KHAN S A, VAN DAM T, et al. The use of GPS horizontals for loading studies, with applications to northern California and southeast Greenland[J]. Journal of Geophysical Research: Solid Earth, 2013, 118(4): 1795-1806. DOI:10.1002/jgrb.50104 |
| [19] |
归庆明, 黄维彬, 张建军. 抗差泛岭估计[J]. 测绘学报, 1998, 27(3): 211-216. GUI Qingming, HUANG Weibin, ZHANG Jianjun. Robust universal ridge estimation[J]. Acta Geodaetica et Cartographic Sinica, 1998, 27(3): 211-216. |
| [20] |
TIKHONOV A N, ARSENIN V Y. Solutions of ill-posed problems[M]. Washington DC: Halsted Press, 1977.
|
| [21] |
LONGMAN I M. A Green's function for determining the deformation of the Earth under surface mass loads: 2. Computations and numerical results[J]. Journal of Geophysical Research, 1963, 68(2): 485-496. DOI:10.1029/JZ068i002p00485 |
| [22] |
王振杰, 欧吉坤. 用L-曲线法确定岭估计中的岭参数[J]. 武汉大学学报(信息科学版), 2004, 29(3): 235-238. WANG Zhenjie, OU Jikun. Determining the ridge parameter in a ridge estimation using L-curve method[J]. Geomatics and Information Science of Wuhan University, 2004, 29(3): 235-238. |
| [23] |
胡明城. 现代大地测量学的理论及其应用[M]. 北京: 测绘出版社, 2003: 362-384. HU Mingcheng. The theory and the application of contemporary geodesy[M]. Beijing: Surveying and Mapping Press, 2003: 362-384. |
| [24] |
HOBSON E W. The theory of spherical and ellipsoidal harmonics[M]. New York: Chelsea Publishing Company, 1955.
|
| [25] |
BATES A P, KHALID Z, KENNEDY R A. Slepian spatial-spectral concentration problem on the sphere: analytical formulation for limited colatitude-longitude spatial region[J]. IEEE Transactions on Signal Processing, 2017, 65(6): 1527-1537. DOI:10.1109/TSP.2016.2646668 |
| [26] |
SIMONS F J, DAHLEN F A. Spherical Slepian functions and the polar gap in geodesy[J]. Geophysical Journal International, 2006, 166(3): 1039-1061. DOI:10.1111/j.1365-246X.2006.03065.x |
| [27] |
FOK H S, LIU Yongxin. An improved GPS-inferred seasonal terrestrial water storage using terrain-corrected vertical crustal displacements constrained by GRACE[J]. Remote Sensing, 2019, 11(12): 1433. DOI:10.3390/rs11121433 |
| [28] |
ARGUS D F, FU Yuning, LANDERER F W. Seasonal variation in total water storage in California inferred from GPS observations of vertical land motion[J]. Geophysical Research Letters, 2014, 41(6): 1971-1980. DOI:10.1002/2014GL059570 |



