2. 华中科技大学地球物理研究所, 湖北 武汉 430074;
3. 华北水利水电大学测绘与地理信息学院, 河南 郑州 450045
2. Institute of Geophysics, Huazhong University of Science and Technology, Wuhan 430074, China;
3. School of Surveying, Mapping and Geographic Information, North China University of Water Resources and Electric Power, Zhengzhou 450045, China
时变重力场综合反映了地球表层与内部空间物质的运移规律,研究地球重力场随时间的变化,既是大地测量学的核心课题之一,也是人类研究自然灾害的重要手段。利用卫星重力手段监测时变重力场的研究可追溯到20世纪60年代,文献[1]提出高低卫星跟踪卫星模式,文献[2]提出低低卫星跟踪卫星模式理论,卫星跟踪卫星理论的相继提出为后续研究重力卫星奠定了坚实的理论基础。21世纪以来,CHAMP(challenging minisate-llite payload)、GRACE(gravity recovery and climate experiment)、GRACE Follow-On(gravity recovery and climate experiment follow-on)和GOCE(gravity field and steady-state ocean circulation explorer)卫星的成功实施,使得卫星重力进入新时代,也为时变重力场建模及应用提供了重要的数据基础。
国内外研究人员利用卫星时变重力场模型开展了大量的应用研究工作,取得了丰硕的研究成果,主要包括全球或区域水储量变化、冰盖质量变化、海平面变化、地震监测等[3-13]。文献[3]使用GRACE时变重力场模型研究了中国黑河流域地下水变化,结果表明卫星监测结果与实测结果有很好的一致性。文献[4]采用6种不同的时变重力场模型估算长江流域水储量变化,成功监测到了长江流域发生的干旱事件。文献[9]利用GRACE数据分析了长江流域水储量季节性的变化特征,发现长江流域水储量变化的周年振幅可达3.4 cm。文献[10]利用GRACE时变重力场数据,研究了中国及周边地区的水储量变化。文献[11]采用GRACE月尺度重力场模型,估算全球陆地水储量变化,揭示了陆地水储量的季节性变化与长期性变化。文献[12]采用GRACE重力场模型计算中国水储量,并联合实测数据研究了中国地区的干旱事件。文献[13]联合GPS与GRACE数据探测中国西南地区的干旱,揭示了GPS数据在干旱检测中的可靠性与优势。
GRACE重力卫星能够实时监测地球重力场变化,提供全球高精度时变重力场信息,而如何从卫星数据中精确提取重力场信号一直是卫星重力研究的热点与难点。目前,除了CSR(Center of Space Research)、JPL(Jet Propulsion Laboratory)、GFZ(German Research Centre for Geosciences)官方机构最新发布的RL06产品[14],国内外多家机构也陆续公布了自主研制的时变重力场模型。国际时变重力场模型联合解算组织COST-G联合AIUB(Astronomical Institute, University of Bern)、GRGS(Groupe de Research en Geodesie Spatial)、GFZ与ITSG(Institute of Geodesy at Graz University of Technology)等机构的解算优势[15],发布了GRACE、GRACE-FO及Swarm的联合解算模型,使得时变重力场模型的精度得到进一步提升;华中科技大学也基于改进的动力法解算,发布了HUST-Grace2020时变重力场模型[16]。本文将首先对比最新发布的HUST-Grace2020模型与COST-G模型、CSR RL06模型、ITSG-Grace2018模型和Tongji-Grace2018模型,评估HUST-Grace2020估算中国大陆区域陆地水储量变化的能力,并在此基础上研究中国大陆典型流域的水储量变化特征。
1 研究区概况我国地处北半球欧亚大陆东部,太平洋的西部,幅员辽阔且地形复杂。我国土地资源和水资源呈现相反的空间散布趋势,这种特征加剧了我国水资源短缺的矛盾。由于我国具有特殊的季风气候,区域降水年际变动较大,在时间上表现为雨热同期的特点,降水多表现为夏秋季多,冬春季少,易成春旱夏涝。因此,及时掌握我国水储量的变化和水资源分布的时间特征与空间规律,对水资源的持续利用具有指导性意义。根据我国大陆区域河流湖泊的分布特点,研究区划分为15个区域[17](图 1),每个区域的具体信息见表 1。
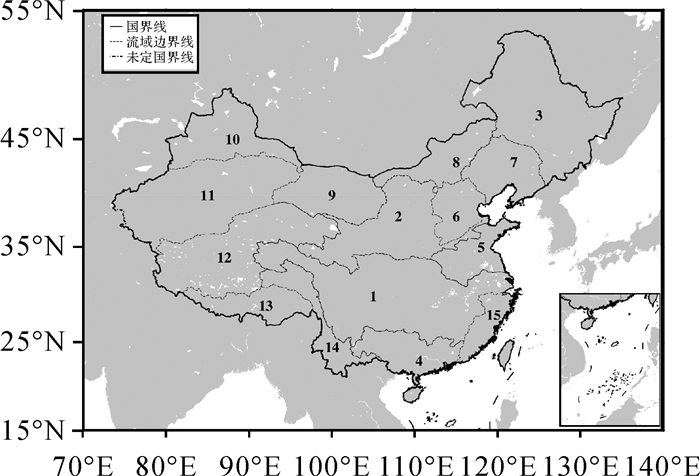
|
| 图 1 研究区划分 Fig. 1 The study area division |
| 编号 | 区域名称 | 流域面积/(×105 km2) | 子流域数量 |
| 1 | 长江流域 | 17.7 | 7 |
| 2 | 黄河流域 | 8.4 | 5 |
| 3 | 松花江流域 | 9.3 | 3 |
| 4 | 珠江流域 | 5.4 | 2 |
| 5 | 淮河流域 | 3.3 | 2 |
| 6 | 海河流域 | 2.7 | 2 |
| 7 | 辽滦流域 | 3.7 | 2 |
| 8 | 内蒙古 | 3.1 | 1 |
| 9 | 河西 | 4.4 | 1 |
| 10 | 准格尔盆地 | 4.8 | 3 |
| 11 | 塔里木盆地 | 11.1 | 4 |
| 12 | 西藏 | 10.5 | 4 |
| 13 | 雅鲁藏布江 | 6.5 | 3 |
| 14 | 澜沧江 | 3.8 | 2 |
| 15 | 东南海岸 | 2.5 | 1 |
2 数据处理方法
大地水准面的变化ΔN反映了地球质量迁移,这种变化能够通过球谐系数的变化ΔClm、ΔSlm表现出来。引起大地水准面变化的物质密度变化为Δρ(r, θ, λ),对其进行径向积分可以得到单位面积上质量的改变量Δσ(θ, λ)。令等效水高(equivalent water height,EWH)的变化量为ΔH,且有ΔH=Δσ/ρw,则等效水高表示的地表质量变化[18]可表示为
 (1)
(1)
式中,a表示地球的平均半径;ρave为地球的平均密度;ρw=1000 kg/m3为水体的密度;l与m分别表示球谐系数的阶数与次数;θ、λ分别表示该点的地心余纬与地心经度;ΔClm、ΔSlm为球谐系数的变化;kl为负荷勒夫数;Plm为完全规格化勒让德缔合(Legendre)函数。
GRACE时变重力场模型存在高频误差和高频噪声[19],直接使用式(1)估算的等效水高在空域内呈现为明显的南北条带误差。为了削弱南北条带误差与高频噪声的影响,国内外学者相继提出了高斯滤波[20]、扇形滤波[21]和去相关滤波[22]等滤波方法。本文采用300 km高斯滤波与P3M6去相关滤波的组合滤波方法[3],其中组合滤波处理后的EWH计算公式为
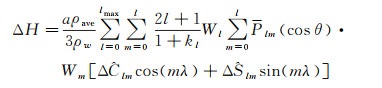 (2)
(2)
式中,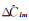
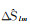
 (3)
(3)
进行去相关滤波处理之后,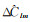
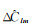
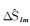
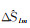
经过上述处理得到全球各个格网点等效水高值,结合不同流域的边界数据,按照流域面积进行加权平均,进而计算出各个流域的平均水储量变化,计算公式为
 (4)
(4)
本文采用华中科技大学发布的HUST-Grace2020模型、COST-G发布的联合解算模型、CSR发布的RL06重力场模型、ITSG发布的ITSG-Grace2018模型,以及同济大学发布的Tongji-Grace2018模型计算中国区域水储量的变化。5种重力场模型的时间范围均为2003年1月—2016年7月,其中HUST-Grace2020(截断至60阶次和90阶次)、ITSG-Grace2018(截断至60阶次和90阶次)和Tongji-Grace2018(截断至90阶次)为147个月,有16个月份数据缺失;COST-G(截断至90阶次)和CSR RL06(截断至60阶次)为148个月,有15个月份数据缺失。在等效水高计算过程中,将SLR的C20项替换掉GRACE的C20[23],加回C10、C11与S11项[24-25],并扣除研究时间范围内球谐系数的平均值。
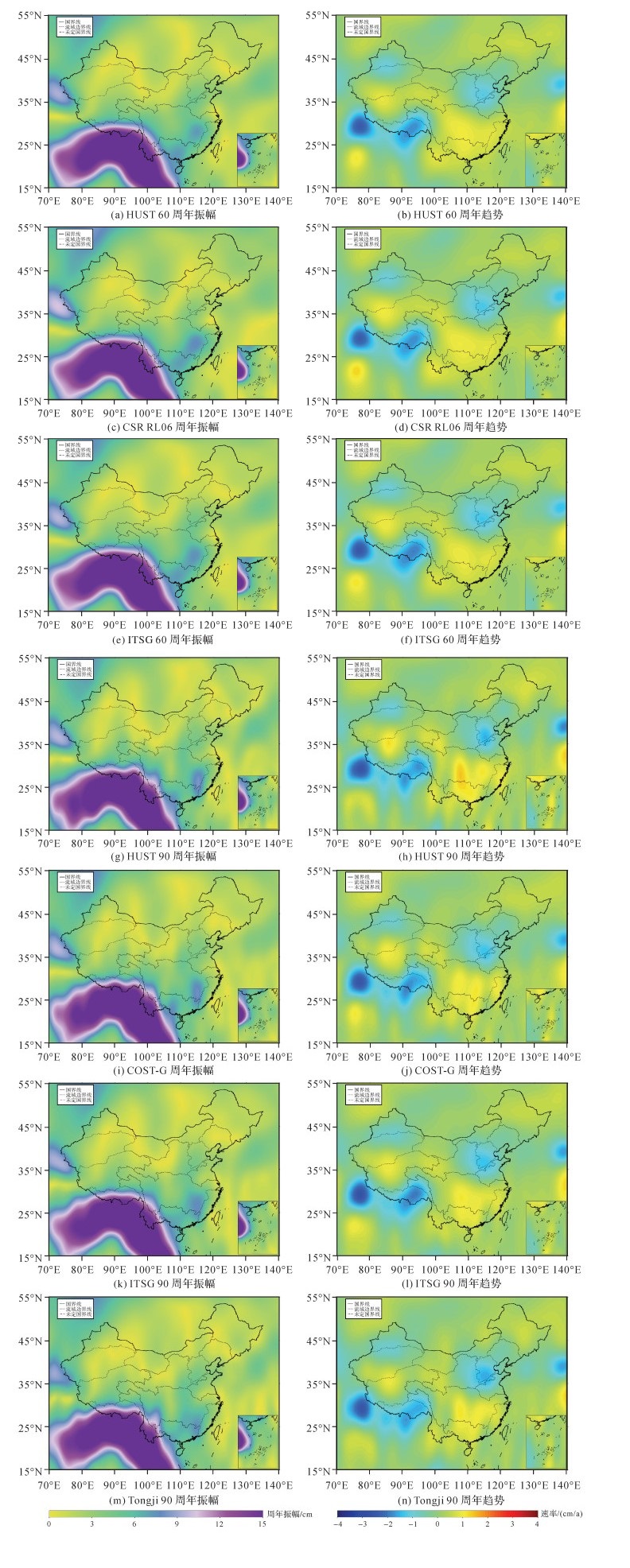
3 结果与分析 3.1 中国大陆水储量变化的总体规律采用HUST-Grace2020 60阶(HUST 60)、CSR RL06 60阶(CSR RL06)、ITSG-Grace2018 60阶(ITSG 60)、HUST-Grace2020 90阶(HUST 90)、COST-G 90阶(COST-G)、ITSG-Grace2018 90阶(ITSG 90)和Tongji-Grace2018 90阶(Tongji 90)重力场模型分别计算了2003年1月—2016年7月中国区域水储量变化,并估算了中国区域的周年趋势与周年振幅(图 2)。
|
| 图 2 2003—2017年中国大陆水储量变化周年振幅与周年趋势 Fig. 2 The annual amplitude and yearly trend of TWS variations from 2003 to 2017 in Chinese mainland |
由图 2可知,5种模型反演结果具有很好的一致性:截断至60阶次时,HUST-Grace2020模型与ITSG-Grace2018模型的估算结果一致性高,相关系数达到0.999且均方根误差为0.136 cm;截断至90阶次时,HUST-Grace2020模型与COST-G模型的估算结果一致性高,相关系数达到0.998且均方根误差为0.204 cm;不同截断阶次的结果在空间分布特征上较为一致,由于高频噪声的影响,截断至90阶次的结果仍存在部分条带误差。在此基础上,分析了我国大陆区域水储量变化的总体变化规律:①我国东南地区及西南边界具有较大的周年振幅(图 2(a)、(c)、(e)、(g)、(i)、(k)、(m))。②我国大陆区域的水储量在各个流域表现为不同的变化趋势(图 2(b)、(d)、(f)、(h)、(j)、(l)、(n))。长江流域中南部、珠江流域、东南沿海、澜沧江南部、塔里木盆地南部、西藏流域北部、松花江流域的陆地水储量呈现增加趋势,而黄河流域东部、海河流域、淮河流域北部、辽滦流域、准格尔盆地与塔里木盆地交界处、西南地区的雅鲁藏布江的陆地水储量呈现递减趋势。
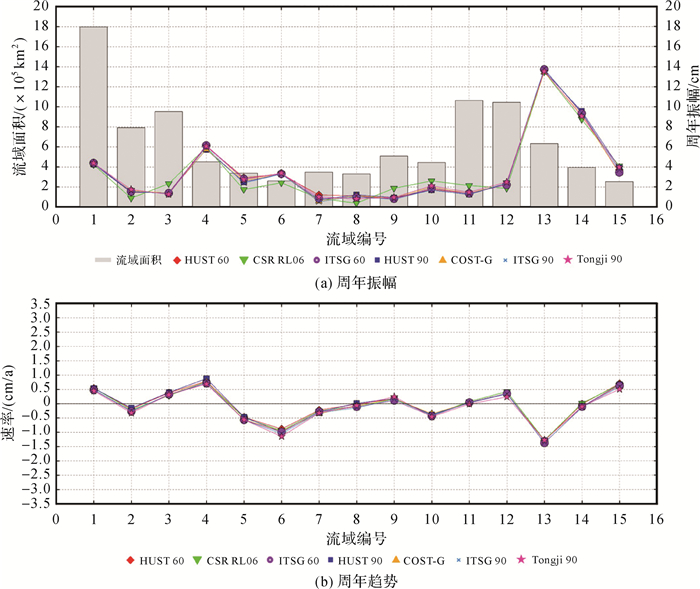
为进一步评估流域尺度上5种模型的结果,本文估算了不同流域水储量变化的周年振幅、半周年振幅、周年相位、半周年相位、周年趋势等特征信息,结果如图 3和表 2所示。结果表明:①5种GRACE产品计算出的各流域水储量变化趋势相互吻合,不同产品反演出的流域水储量变化幅度基本一致。②雅鲁藏布江水储量振幅最大,可达13.75 cm,这与该流域水资源丰富、冰川众多有关;变化幅度较小的流域为辽滦流域、内蒙古、河西与塔里木流域,这些地区普遍位于我国北部,且大部分处在我国西北内陆部分,常年降雨量少,水资源无法得到及时补充。
|
| 图 3 2003—2017年中国大陆各个流域水储量变化振幅与趋势 Fig. 3 The annual amplitude and trend of TWS variations in Chinese mainland basins from 2003 to 2017 |
| 流域编号 | HUST 60 | CSR RL06 | ITSG 60 | HUST 90 | COST-G | ITSG 90 | Tongji 90 | |||||||||||||
| 振幅/cm | 速率/(cm/a) | 振幅/cm | 速率/(cm/a) | 振幅/cm | 速率/(cm/a) | 振幅/cm | 速率/(cm/a) | 振幅/cm | 速率/(cm/a) | 振幅/cm | 速率/(cm/a) | 振幅/cm | 速率/(cm/a) | |||||||
| 1 | 4.30 | 0.54 | 4.23 | 0.54 | 4.40 | 0.48 | 4.28 | 0.54 | 4.26 | 0.49 | 4.31 | 0.49 | 4.38 | 0.45 | ||||||
| 2 | 1.47 | -0.18 | 0.89 | -0.22 | 1.56 | -0.27 | 1.49 | -0.15 | 1.63 | -0.28 | 1.57 | -0.25 | 1.75 | -0.32 | ||||||
| 3 | 1.42 | 0.38 | 2.33 | 0.29 | 1.38 | 0.33 | 1.39 | 0.39 | 1.41 | 0.32 | 1.36 | 0.31 | 1.26 | 0.31 | ||||||
| 4 | 6.09 | 0.78 | 5.97 | 0.75 | 6.15 | 0.71 | 5.74 | 0.88 | 5.75 | 0.77 | 5.96 | 0.75 | 6.06 | 0.69 | ||||||
| 5 | 2.93 | -0.47 | 1.74 | -0.49 | 2.81 | -0.55 | 2.49 | -0.47 | 2.63 | -0.56 | 2.38 | -0.57 | 2.75 | -0.56 | ||||||
| 6 | 3.27 | -0.88 | 2.42 | -0.94 | 3.31 | -0.99 | 3.29 | -0.99 | 3.34 | -0.95 | 3.29 | -1.05 | 3.38 | -1.14 | ||||||
| 7 | 1.21 | -0.22 | 0.87 | -0.25 | 0.85 | -0.28 | 0.69 | -0.28 | 0.57 | -0.35 | 0.53 | -0.32 | 1.01 | -0.32 | ||||||
| 8 | 1.11 | -0.01 | 0.37 | -0.09 | 0.97 | -0.11 | 1.22 | 0.01 | 1.14 | -0.08 | 1.07 | -0.15 | 0.82 | -0.06 | ||||||
| 9 | 0.82 | 0.17 | 1.87 | 0.16 | 0.83 | 0.11 | 0.94 | 0.18 | 0.92 | 0.17 | 0.76 | 0.15 | 0.95 | 0.25 | ||||||
| 10 | 1.77 | -0.40 | 2.60 | -0.40 | 1.88 | -0.43 | 1.69 | -0.38 | 1.99 | -0.35 | 1.70 | -0.41 | 2.11 | -0.46 | ||||||
| 11 | 1.37 | 0.02 | 2.14 | 0.08 | 1.36 | 0.04 | 1.25 | 0.05 | 1.37 | 0.04 | 1.28 | 0.03 | 1.48 | -0.01 | ||||||
| 12 | 2.31 | 0.35 | 1.87 | 0.42 | 2.21 | 0.35 | 2.36 | 0.36 | 2.36 | 0.34 | 2.39 | 0.34 | 2.49 | 0.24 | ||||||
| 13 | 13.75 | -1.30 | 13.50 | -1.27 | 13.74 | -1.37 | 13.56 | -1.28 | 13.46 | -1.28 | 13.79 | -1.36 | 13.54 | -1.27 | ||||||
| 14 | 9.37 | -0.01 | 8.75 | 0.01 | 9.35 | -0.11 | 9.57 | -0.10 | 9.18 | -0.11 | 9.44 | -0.13 | 9.05 | -0.10 | ||||||
| 15 | 3.71 | 0.70 | 4.11 | 0.67 | 3.45 | 0.63 | 3.93 | 0.68 | 3.39 | 0.66 | 3.68 | 0.60 | 3.97 | 0.51 | ||||||
对不同产品得出的周年振幅项与周年趋势项求相关系数与均方根误差,结果如表 3—表 6所示。其中,不同产品之间的周年振幅相关系数达0.98以上,而周年趋势的相关系数均为0.99以上。不同产品间的周年趋势均方根误差基本都在0.1 cm/a以下,但周年振幅均方根误差最小为0.136 cm。综合分析周年振幅与周年趋势的统计结果,发现HUST-Grace2020 60阶模型与ITSG-Grace2018 60阶模型一致性最好,HUST-Grace2020 90阶模型与COST-G 90阶模型的一致性最好。由于COST-G与ITSG-Grace2018模型具有较高的解算精度,而HUST-Grace2020模型与它们的一致性也是最好的,因此可以证明HUST-Grace2020模型能够很好地评估中国大陆区域水储量的变化。
| 模型 | HUST 60 | CSR RL06 | ITSG 60 | HUST 90 | COST-G | ITSG 90 | Tongji 90 |
| HUST 60 | 1 | 0.980 | 0.999 | 0.998 | 0.998 | 0.998 | 0.998 |
| CSR RL06 | 0.980 | 1 | 0.981 | 0.981 | 0.981 | 0.982 | 0.983 |
| ITSG 60 | 0.999 | 0.981 | 1 | 0.998 | 0.999 | 0.999 | 0.999 |
| HUST 90 | 0.998 | 0.981 | 0.998 | 1 | 0.999 | 0.999 | 0.998 |
| COST-G | 0.998 | 0.981 | 0.999 | 0.999 | 1 | 0.999 | 0.998 |
| ITSG 90 | 0.998 | 0.982 | 0.999 | 0.999 | 0.999 | 1 | 0.998 |
| Tongji 90 | 0.998 | 0.983 | 0.999 | 0.998 | 0.998 | 0.998 | 1 |
| 模型 | HUST 60 | CSR RL06 | ITSG 60 | HUST 90 | COST-G | ITSG 90 | Tongji 90 |
| HUST 60 | 1 | 0.997 | 0.998 | 0.997 | 0.996 | 0.996 | 0.990 |
| CSR RL06 | 0.997 | 1 | 0.998 | 0.994 | 0.996 | 0.998 | 0.990 |
| ITSG 60 | 0.998 | 0.998 | 1 | 0.997 | 0.997 | 0.999 | 0.991 |
| HUST 90 | 0.997 | 0.994 | 0.997 | 1 | 0.997 | 0.998 | 0.993 |
| COST-G | 0.996 | 0.996 | 0.997 | 0.997 | 1 | 0.998 | 0.992 |
| ITSG 90 | 0.996 | 0.998 | 0.999 | 0.998 | 0.998 | 1 | 0.994 |
| Tongji 90 | 0.990 | 0.990 | 0.991 | 0.993 | 0.992 | 0.994 | 1 |
| 模型 | HUST 60 | CSR RL06 | ITSG 60 | HUST 90 | COST-G | ITSG 90 | Tongji 90 |
| HUST 60 | 0 | 0.691 | 0.136 | 0.226 | 0.249 | 0.235 | 0.212 |
| CSR RL06 | 0.691 | 0 | 0.678 | 0.674 | 0.662 | 0.682 | 0.638 |
| ITSG 60 | 0.136 | 0.678 | 0 | 0.227 | 0.179 | 0.966 | 0.212 |
| HUST 90 | 0.226 | 0.674 | 0.227 | 0 | 0.204 | 0.138 | 0.265 |
| COST-G | 0.249 | 0.662 | 0.179 | 0.204 | 0 | 0.183 | 0.240 |
| ITSG 90 | 0.235 | 0.682 | 0.966 | 0.138 | 0.183 | 0 | 0.264 |
| Tongji 90 | 0.212 | 0.638 | 0.212 | 0.240 | 0.240 | 0.264 | 0 |
| 模型 | HUST 60 | CSR RL06 | ITSG 60 | HUST 90 | COST-G | ITSG 90 | Tongji 90 |
| HUST 60 | 0 | 0.047 | 0.071 | 0.050 | 0.066 | 0.086 | 0.115 |
| CSR RL06 | 0.047 | 0 | 0.059 | 0.065 | 0.056 | 0.070 | 0.104 |
| ITSG 60 | 0.071 | 0.059 | 0 | 0.077 | 0.045 | 0.030 | 0.078 |
| HUST 90 | 0.050 | 0.065 | 0.077 | 0 | 0.064 | 0.079 | 0.108 |
| COST-G | 0.066 | 0.056 | 0.045 | 0.064 | 0 | 0.046 | 0.082 |
| ITSG 90 | 0.086 | 0.070 | 0.030 | 0.079 | 0.046 | 0 | 0.067 |
| Tongji 90 | 0.115 | 0.104 | 0.078 | 0.108 | 0.082 | 0.067 | 0 |
以截断至60阶次HUST-Grace2020的计算结果为基础,总结了中国大陆区域水储量的变化特征:①长江流域、松花江流域、珠江流域、河西、西藏、东南沿海地区呈现增加趋势,黄淮海地区、辽滦流域、准格尔流域、雅鲁藏布江呈减少趋势;②珠江流域水储量增加速度最快,可达0.78 cm/a,其中珠江流域北部受到三峡水库蓄水的影响,水储量增长速度较快,而珠江流域西部地区降水较少,水储量将近处于持平状态,该结果与文献[26]反演出的珠江流域水储量增速3~5 mm/a一致;③雅鲁藏布江存在严重的水储量减少信号,下降速率可达到-1.30 cm/a;④位于华北地区的黄河、淮河与海河流域水储量也处于亏损状态,亏损速率分别为-0.18、-0.47、-0.88 cm/a,其原因可能与近些年这些地区地下水过度开采有关,该结果与文献[27]反演出的华北地区等效水高变化率为-1.0~-0.5 cm/a相符。
3.2 流域尺度的水储量变化规律为研究流域尺度的水储量季节性变化特征,本文选取2006年与2010年两个特征年份,采用HUST-Grace2020 60阶模型估算了中国大陆区域不同季节的等效水高,结果如图 4所示。

|
| 图 4 2006年与2010年等效水高 Fig. 4 EWH in 2006 and 2010 |
12月、1月及2月属于冬季,由图 4(a)与(b)可知,2005年冬季黄淮海地区及新疆北部水储量为盈余状态,主要与该年份的降水增多有关[28-29],但长江流域、珠江流域、东北地区与西南地区均处于亏损状态;而2009年冬季表现为全国大部分地区处于水储量亏损状态。3—5月属于春季,由图 4(c)和(d)可知,2006年与2010年中国东南沿海区域、东北地区的松花江流域与辽滦流域的水储量均呈现盈余状态,而西南地区、西藏、珠江流域西部在春季仍然表现为亏损状态,这是由于季风气候在春季还未到达大陆内部,存在降水滞后。6—8月属于夏季,由图 4(e)可知,2006年夏季长江流域的部分区域出现水储量亏损,说明该流域存在干旱事件。由图 4(f)可知,2010年夏季长江中下游、珠江流域、黄河上游等地区水储量均表现为盈余状态。9—11月属于秋季,由图 4(g)可知,我国中部及西南边界地区水储量呈现盈余状态,其余地区水量表现为亏损状态;由图 4(h)可知,全国大部分地区在2010年秋季水量仍处于盈余状态,尤其是我国中东部以及东南沿海地区。
综上,我国大陆区域的水储量变化表现为显著的季节性特征,南方比北方的季节性特征更为显著。受到太平洋气流的影响,我国夏秋两季多雨,容易出现洪涝灾害事件,春冬两季降雨相对较少,容易出现干旱事件。
3.3 典型流域的水文事件长江流域与黄河流域作为我国两大流域,及时掌握其水储量变化,评估发生的水文事件,对水资源的持续利用具有指导性意义。本文分别利用5种模型计算了长江流域与黄河流域的水储量随时间变化序列,结果如图 5(a)和图 6(a)所示。特别地,为了分析典型流域的水文事件,从原始时间序列中剔除了长期趋势、周年、半周年等季节性信号,得到典型流域水储量变化的非季节性信息[30],结果如图 5(b)和图 6(b)所示。由于不同机构重力场模型的解算方法存在差异,且随着模型阶数增加高频误差增大,再加上GRACE卫星在不同时期的观测精度不同,得到的时间序列结果在部分月份差异较大,因此本文统一采用HUST-Grace2020截断至60阶模型的反演结果分析典型流域的水文事件。

|
| 图 5 2003—2017年长江流域时间序列 Fig. 5 Time series of the Yangtze River Basin from 2003 to 2017 |

|
| 图 6 2003—2017年黄河流域时间序列 Fig. 6 Time series of the Yellow River Basin from 2003 to 2017 |
为了定量分析不同机构计算的长江流域水储量时间序列,本文计算了不同产品间时间序列的相关系数与均方根误差,结果如表 7—表 8所示。通过分析表 7—表 8可知,HUST-Grace2020模型计算的长江流域水储量变化与ITSG-Grace2018和COST-G产品结果一致性最好,其中HUST 60阶模型与ITSG 60阶模型相关系数和均方根误差分别为0.983与0.797 cm,HUST 90阶模型与COST-G 90阶模型相关系数和均方根误差分别为0.985与0.752 cm,因此HUST-Grace2020模型可用于研究该流域的典型水文事件。由图 5(a)可知,长江流域在2006年与2011年出现谷值;结合去除季节性信号后的图 5(b)可知,2006年该流域水储量变化幅度最大。根据等效水高结果分析长江流域水储量变化,2006年夏秋季节该流域水储量减少;而该流域在2011年从春季开始减少,7月时出现小幅度回升,但随即又减少,直到10月才开始回升。通过上述分析可知,长江流域在2006年与2011年发生极端干旱事件。图 5中2010年与2016年出现水储量峰值,表明这两年长江流域发生洪水事件。根据《长江流域及西南诸河水资源公报》[31]发现:2006年8月长江流域入海量极低,远低于史上最干旱的1978年入海量,2011年3月起长江流域各支流水位处于历史最低标准;2010年长江流域受到降雨影响水位达到近20年的最大值,2016年长江中下游地区发生特大洪水。本文得到的长江流域干旱洪水年份结果与文献[32]研究结果基本一致。
| 模型 | HUST 60 | CSR RL06 | ITSG 60 | HUST 90 | COST-G | ITSG 90 | Tongji 90 |
| HUST 60 | 1 | 0.975 | 0.983 | 0.995 | 0.983 | 0.982 | 0.966 |
| CSR RL06 | 0.975 | 1 | 0.970 | 0.971 | 0.968 | 0.970 | 0.955 |
| ITSG 60 | 0.983 | 0.970 | 1 | 0.978 | 0.989 | 0.998 | 0.978 |
| HUST 90 | 0.995 | 0.971 | 0.978 | 1 | 0.985 | 0.979 | 0.964 |
| COST-G | 0.983 | 0.968 | 0.989 | 0.985 | 1 | 0.993 | 0.984 |
| ITSG 90 | 0.982 | 0.970 | 0.979 | 0.979 | 0.993 | 1 | 0.981 |
| Tongji 90 | 0.966 | 0.955 | 0.964 | 0.984 | 0.984 | 0.981 | 1 |
| 模型 | HUST 60 | CSR RL06 | ITSG 60 | HUST 90 | COST-G | ITSG 90 | Tongji 90 |
| HUST 60 | 0 | 0.963 | 0.797 | 1.277 | 0.434 | 0.800 | 1.106 |
| CSR RL06 | 0.963 | 0 | 1.030 | 1.038 | 1.061 | 1.026 | 1.277 |
| ITSG 60 | 0.797 | 1.030 | 0 | 0.906 | 0.624 | 0.260 | 0.874 |
| HUST 90 | 1.277 | 1.03 | 0.906 | 0 | 0.752 | 0.873 | 1.146 |
| COST-G | 0.434 | 1.061 | 0.624 | 0.752 | 0 | 0.480 | 0.743 |
| ITSG 90 | 0.800 | 1.026 | 0.260 | 0.873 | 0.480 | 0 | 0.823 |
| Tongji 90 | 1.106 | 1.277 | 0.874 | 1.146 | 0.743 | 0.823 | 0 |
由图 6可知,各个机构模型计算结果的一致性高,且黄河流域水储量变化波动幅度小。为了定量分析不同机构计算的黄河流域水储量时间序列,计算的不同产品间时间序列相关系数与均方根误差如表 9—表 10所示。由表 9—表 10可知,HUST-Grace2020模型计算的黄河流域水储量变化与CSR RL06和COST-G产品结果一致性最好,其中HUST 60阶模型与CSR RL06模型相关系数和均方根误差分别为0.893与0.974 cm,HUST 90阶模型与COST-G 90阶模型相关系数和均方根误差分别为0.882和1.175 cm。由图 6可知,2003年黄河流域水储量变化出现谷值,其中3月的等效水高为-4.97 cm;2013年7月黄河流域出现水储量峰值且该月的等效水高为4.01 cm,由此说明2003年黄河流域发生极端干旱事件,2013年发生洪水事件。《黄河水资源公报》[33]显示:2002年黄河流域花园口水文站径流比平均径流少了约52%,该年是黄河流域有史以来最干旱的一年,旱情持续至第二年春,因此导致2003年黄河流域出现水储量谷值;而2013年黄河中上游多次发生暴雨,部分监测站出现建站以来最高水位。本文计算结果与水文资料相符。需要特别指出的是,图 6(a)与图 6(b)中显示黄河流域在2004年9月出现水储量出现峰值,该峰值并不是洪水事件信号,而是与GRACE星下点轨迹过于稀疏有关。
| 模型 | HUST 60 | CSR RL06 | ITSG 60 | HUST 90 | COST-G | ITSG 90 | Tongji 90 |
| HUST 60 | 1 | 0.893 | 0.896 | 0.891 | 0.881 | 0.870 | 0.796 |
| CSR RL06 | 0.893 | 1 | 0.831 | 0.811 | 0.869 | 0.864 | 0.803 |
| ITSG 60 | 0.896 | 0.831 | 1 | 0.831 | 0.932 | 0.978 | 0.866 |
| HUST 90 | 0.891 | 0.811 | 0.831 | 1 | 0.882 | 0.868 | 0.838 |
| COST-G | 0.881 | 0.869 | 0.932 | 0.882 | 1 | 0.960 | 0.928 |
| ITSG 90 | 0.870 | 0.864 | 0.978 | 0.868 | 0.960 | 1 | 0.898 |
| Tongji 90 | 0.796 | 0.803 | 0.866 | 0.838 | 0.928 | 0.898 | 1 |
| 模型 | HUST 60 | CSR RL06 | ITSG 60 | HUST 90 | COST-G | ITSG 90 | Tongji 90 |
| HUST 60 | 0 | 0.974 | 1.046 | 1.055 | 1.169 | 1.177 | 1.727 |
| CSR RL06 | 0.974 | 0 | 1.107 | 1.351 | 1.244 | 1.205 | 1.730 |
| ITSG 60 | 1.046 | 1.107 | 0 | 1.355 | 0.896 | 0.498 | 1.428 |
| HUST 90 | 1.055 | 1.351 | 1.355 | 0 | 1.175 | 1.205 | 1.553 |
| COST-G | 1.169 | 1.244 | 0.896 | 1.175 | 0 | 0.694 | 1.073 |
| ITSG 90 | 1.177 | 1.205 | 0.498 | 1.205 | 0.694 | 0 | 1.266 |
| Tongji 90 | 1.727 | 1.730 | 1.428 | 1.073 | 1.073 | 1.266 | 0 |
4 总结
本文利用HUST-Grace2020时变重力场模型计算中国大陆区域陆地水储量变化。研究结果表明:①HUST-Grace2020模型计算的结果与COST-G、ITSG、Tongji模型的结果具有极高的相关性,证明了HUST-Grace2020具有估算中国大陆区域陆地水储量变化的能力。②不同流域的水储量变化特征不同。长江流域、珠江流域、雅鲁藏布江及澜沧江有较大的周年振幅。长江流域、松花江流域、珠江流域、河西、西藏与东南沿海地区水储量呈现增加趋势,黄淮海地区、辽滦流域、准格尔流域与雅鲁藏布江水储量呈现递减趋势,其余流域水储量基本维持平衡。③中国大陆地区陆地水储量变化具有显著的季节性特征:夏秋季水储量盈余,冬春季水储量匮乏。④以中国典型流域——长江流域与黄河流域为例,研究了HUST-Grace2020模型监测洪水干旱事件的能力。结果表明:HUST-Grace2020模型可以探测到长江流域在2006年与2011年发生极端干旱事件,2010年与2016年发生洪水事件;黄河流域在2003年出现极端干旱事件,2013年出现洪水事件。
本文仅计算了2003年1月—2016年7月的中国大陆区域陆地水储量变化,未来考虑结合GRACE-FO模型及数据重构技术,计算时间跨度更长的陆地水储量变化。此外,现阶段COST-G联合解算模型仅纳入了欧洲机构[15],而本文计算结果表明:我国重力场解算机构具备同等的重力场反演能力,也具备服务于COST-G组织的能力,未来可为解算更高精度的时变重力场模型贡献中国力量[34]。
| [1] |
BAKER R M. Orbit determination from range and range-rate data[C]//Proceedings of 1960 Semi-Annual Meeting of the American Rocket Society. Los Angeles: ARS, 1960: 1220-1260.
|
| [2] |
WOLFF M. Direct measurements of the Earth's gravitational potential using a satellite pair[J]. Journal of Geophysical Research, 1969, 74(22): 5295-5300. DOI:10.1029/JB074i022p05295 |
| [3] |
罗志才, 李琼, 钟波. 利用GRACE时变重力场反演黑河流域水储量变化[J]. 测绘学报, 2012, 41(5): 676-681. LUO Zhicai, LI Qiong, ZHONG Bo. Water storage variations in Heihe River basin recovered from GRACE temporal gravity field[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 676-681. |
| [4] |
王杰龙, 陈义. 利用GRACE时变重力场数据监测长江流域干旱[J]. 大地测量与地球动力学, 2021, 41(2): 196-200. WANG Jielong, CHEN Yi. Drought detection over Yangtze River basin from GRACE time-variable gravity data[J]. Journal of Geodesy and Geodynamics, 2021, 41(2): 196-200. |
| [5] |
WU Yunlong, ZHAO Qian, ZHANG Bao, et al. Characterizing the seasonal crustal motion in Tianshan area using GPS, GRACE and surface loading models[J]. Remote Sensing, 2017, 9(12): 1303. DOI:10.3390/rs9121303 |
| [6] |
王正涛, 超能芳. 利用SWARM卫星高低跟踪探测格陵兰岛时变重力信号[J]. 地球物理学报, 2014, 57(10): 3117-3128. WANG Zhengtao, CHAO Nengfang. Time-variable gravity signal in Greenland revealed by SWARM high-low satellite-to-satellite tracking[J]. Chinese Journal of Geophysics, 2014, 57(10): 3117-3128. DOI:10.6038/cjg20141003 |
| [7] |
姜磊, 李德庆, 徐志萍, 等. 芦山Ms 7.0地震震前GRACE卫星时变重力场特征研究[J]. 地震学报, 2014, 36(1): 84-94, 158. JIANG Lei, LI Deqing, XU Zhiping, et al. Characteristics of gravity field before the Lushan Ms 7.0 earthquake based on time variable gravity data from GRACE satellite[J]. Acta Seismologica Sinica, 2014, 36(1): 84-94, 158. DOI:10.3969/j.issn.0253-3782.2014.01.007 |
| [8] |
邹正波, 李辉, 吴云龙, 等. 尼泊尔M8.1地震震前卫星重力场时变特征[J]. 大地测量与地球动力学, 2015, 35(4): 547-551. ZOU Zhengbo, LI Hui, WU Yunlong, et al. Characteristics of satellite time-variable gravity field before M8.1 Nepal earthquake[J]. Journal of Geodesy and Geodynamics, 2015, 35(4): 547-551. |
| [9] |
胡小工, 陈剑利, 周永宏, 等. 利用GRACE空间重力测量监测长江流域水储量的季节性变化[J]. 中国科学(D辑: 地球科学), 2006, 36(3): 225-232. HU Xiaogong, CHEN Jianli, ZHOU Yonghong, et al. Monitoring the seasonal variation of water reserves in the Yangtze River basin by GRACE space gravity survey[J]. Science in China (Series D: Earth Sciences), 2006, 36(3): 225-232. |
| [10] |
邢乐林, 李辉, 刘冬至, 等. 利用GRACE时变重力场监测中国及其周边地区的水储量月变化[J]. 大地测量与地球动力学, 2007, 27(4): 35-37, 56. XING Lelin, LI Hui, LIU Dongzhi, et al. Monthly water distribution in China and its adjacent area from time-variable gravity field of GRACE[J]. Journal of Geodesy and Geodynamics, 2007, 27(4): 35-37, 56. |
| [11] |
苏晓莉, 平劲松, 黄倩, 等. 重力卫星检测到的全球陆地水储量变化[J]. 中国科学院上海天文台年刊, 2009(1): 14-21. SU Xiaoli, PING Jinsong, HUANG Qian, et al. The subterranean water time variation in global area by GRACE mission[J]. Annals of Shanghai Astronomical Observatory Chinese Academy of Sciences, 2009(1): 14-21. |
| [12] |
刘任莉, 李建成, 褚永海. 利用GRACE地球重力场模型研究中国西南区域水储量变化[J]. 大地测量与地球动力学, 2012, 32(2): 39-43. LIU Renli, LI Jiancheng, CHU Yonghai. Research on variation of water storage in southwest China by use of GRACE gravity field model[J]. Journal of Geodesy and Geodynamics, 2012, 32(2): 39-43. |
| [13] |
YAO Chaolong, LUO Zhicai, HU Yueming, et al. Detecting droughts in southwest China from GPS vertical position displacements[J]. Journal of Geodesy and Geoinformation Science, 2020, 3(2): 114. |
| [14] |
王正涛, 姜卫平, 晁定波. 卫星跟踪卫星测量确定地球重力场的理论和方法[M]. 武汉: 武汉大学出版社, 2011: 152-153. WANG Zhengtao, JIANG Weiping, CHAO Dingbo. Theory and method of determining the gravity field of the Earth by satellite tracking satellite measurement[M]. Wuhan: Wuhan University Press, 2011: 152-153. |
| [15] |
MEYER U, JEAN Y, KVAS A, et al. Combination of GRACE monthly gravity fields on the normal equation level[J]. Journal of Geodesy, 2019, 93(9): 1645-1658. DOI:10.1007/s00190-019-01274-6 |
| [16] |
ZHOU Hao, ZHOU Zebing, LUO Zhicai. A new hybrid processing strategy to improve temporal gravity field solution[J]. Journal of Geophysical Research: Solid Earth, 2019, 124(8): 9415-9432. DOI:10.1029/2019JB017752 |
| [17] |
YI Shuang, WANG Qiuyu, SUN Wenke. Basin mass dynamic changes in China from GRACE based on a multibasin inversion method[J]. Journal of Geophysical Research: Solid Earth, 2016, 121(5): 3782-3803. DOI:10.1002/2015JB012608 |
| [18] |
JEKELI C. Alternative methods to smooth the Earth's gravity field[R]. Columbus: Ohio State University, 1981.
|
| [19] |
周新, 邢乐林, 邹正波, 等. GRACE时变重力场的高斯平滑研究[J]. 大地测量与地球动力学, 2008, 28(3): 41-45. ZHOU Xin, XING Lelin, ZOU Zhengbo, et al. Study on Gaussian smoothing of grace temporal gravity variation[J]. Journal of Geodesy and Geodynamics, 2008, 28(3): 41-45. |
| [20] |
HAN S C, SHUM C K, JEKELI C, et al. Non-isotropic filtering of GRACE temporal gravity for geophysical signal enhancement[J]. Geophysical Journal International, 2005, 163(1): 18-25. DOI:10.1111/j.1365-246X.2005.02756.x |
| [21] |
ZHANG Z, CHAO B F, LU Y, et al. An effective filtering for GRACE time-variable gravity: fan filter[J]. Geophysical Research Letters, 2009, 36(17): L17311. |
| [22] |
SWENSON S, WAHR J. Post-processing removal of correlated errors in GRACE data[J]. Geophysical Research Letters, 2006, 33(8): L08402. |
| [23] |
CHENG M K, TAPLEY B D, RIES J C. Deceleration in the Earth's oblateness[J]. Journal of Geophysical Research: Solid Earth, 2013, 118(2): 740-747. DOI:10.1002/jgrb.50058 |
| [24] |
SWENSON S, CHAMBERS D, WAHR J. Estimating geocenter variations from a combination of GRACE and ocean model output[J]. Journal of Geophysical Research: Solid Earth, 2008, 113(B8): B08410. |
| [25] |
SUN Y, RIVA R, DITMAR P. Optimizing estimates of annual variations and trends in geocenter motion and J2 from a combination of GRACE data and geophysical models[J]. Journal of Geophysical Research: Solid Earth, 2016, 121(11): 8352-8370. DOI:10.1002/2016JB013073 |
| [26] |
陈智伟, 张兴福, 冉将军, 等. 利用新版GRACE时变模型反演珠江流域陆地水储量变化[J]. 大地测量与地球动力学, 2020, 40(3): 305-310. CHEN Zhiwei, ZHANG Xingfu, RAN Jiangjun, et al. Terrestrial water storage changes in Pearl River region derived from the latest release temporal gravity field models[J]. Journal of Geodesy and Geodynamics, 2020, 40(3): 305-310. |
| [27] |
叶叔华, 苏晓莉, 平劲松, 等. 基于GRACE卫星测量得到的中国及其周边地区陆地水量变化[J]. 吉林大学学报(地球科学版), 2011, 41(5): 1580-1586. YE Shuhua, SU Xiaoli, PING Jinsong, et al. Land water storage variations in China and adjacent areas revealed by the GRACE gravity mission[J]. Journal of Jilin University (Earth Science Edition), 2011, 41(5): 1580-1586. |
| [28] |
束美珍, 杨传国, 李玉龙, 等. 黄淮海地区2003—2014年GRACE水储量时空变化[J]. 南水北调与水利科技, 2018, 16(1): 83-88. SHU Meizhen, YANG Chuanguo, LI Yulong, et al. Temporal and spatial variation of water storage in Huang-Huai-Hai area during 2003—2014 based on GRACE satellite data[J]. South-to-North Water Transfers and Water Science & Technology, 2018, 16(1): 83-88. |
| [29] |
曹艳萍, 南卓铜, 程国栋. GRACE重力卫星监测新疆干旱特征[J]. 干旱区资源与环境, 2015, 29(8): 87-92. CAO Yanping, NAN Zhuotong, CHENG Guodong. GRACE gravity satellite monitoring of drought characteristics in Xinjiang[J]. Journal of Arid Land Resources and Environment, 2015, 29(8): 87-92. |
| [30] |
RAN J, DITMAR P, KLEES R, et al. Statistically optimal estimation of Greenland Ice Sheet mass variations from GRACE monthly solutions using an improved mascon approach[J]. Journal of Geodesy, 2018, 92(3): 299-319. DOI:10.1007/s00190-017-1063-5 |
| [31] |
水利部长江水利委员会. 长江流域及西南诸河水资源公报[EB/OL]. [2022-08-11]. http://cjw.gov.cn/zwzc/bmgb/szygb/. Changjiang Water Resources Commission of the Ministry of Water Resources. Yangtze River basin and southwest rivers water resources bulletin[EB/OL]. [2022-08-11]. http://cjw.gov.cn/zwzc/bmgb/szygb/. |
| [32] |
禤键豪, 陈智伟, 张兴福, 等. 联合GRACE与GRACE-FO反演2002—2020年长江流域陆地水储量变化[J]. 大地测量与地球动力学, 2021, 41(9): 961-966, 972. XUAN Jianhao, CHEN Zhiwei, ZHANG Xingfu, et al. Combining GRACE and GRACE-FO to derive terrestrial water storage changes in the Yangtze River basin from 2002 to 2020[J]. Journal of Geodesy and Geodynamics, 2021, 41(9): 961-966, 972. |
| [33] |
水利部黄河水利委员会. 黄河水资源公报[EB/OL]. [2022-08-11]. http://www.yrcc.gov.cn/zwzc/gzgb/gb/szygb/. Yellow River Conservancy Commission of the Ministry of Water Resources. Yellow River water resources bulletin[EB/OL]. [2022-08-11]. http://www.yrcc.gov.cn/zwzc/gzgb/gb/szygb/. |
| [34] |
MEYER U, LASSER M, JÄGGI A, et al. Combination service for time-variable gravity fields (COST-G): operational GRACE-FO combination and validation of Chinese GRACE time-series[EB/OL]. [2022-10-18]. https://ui.adsabs.harvard.edu/abs/2021EGUGA..23.2416M/abstract.
|



