2. 国防科技大学电子科学学院, 湖南 长沙 410073;
3. 北京化工大学软物质科学与工程高精尖创新中心, 北京 100029
2. College of Electronic Science, National University of Defense Technology, Changsha 410073, China;
3. Beijing Advanced Innovation Center for Soft Matter Science and Engineering, Beijing University of Chemical Technology, Beijing 100029, China
极化目标分解是解释极化合成孔径雷达(polarimetric synthetic aperture radar, PolSAR)数据散射机制的典型方法,在PolSAR图像解译中具有重要意义[1]。近年来,大量目标分解算法被提出,并在PolSAR数据应用中有良好的应用前景,如城市建筑区域提取[2-4]、自然灾害评估[5]、农作物估产、森林参数反演[6-7]及极化图像分类[8-10]等。当前极化目标分解方法主要分为两大类:基于物理模型的分解方法,以及基于特征值特征向量的分解方法。基于物理模型的分解方法由于其简单、准确且易于实现的优点,已经成为PolSAR非相干目标分解的主流方法之一。
基于物理模型的非相干目标分解方法的起源是文献[11]提出的三分量分解方法(freeman Durden decomposition, FDD)。文献[12]引入了可以解释lm(T23)的螺旋散射分量到FDD中,同时也提出了正弦和余弦分布的偶极子云模型来改进FDD的体散射模型,形成了Yamaguchi四分量分解(Yamaguchi original four-component decomposi-tion, Y4O)。
近20年来,大多数的基于模型的极化目标分解方法都是在FDD和Y4O的基础上发展起来的。部分方法通过数学优化的方法以得到更加精细化的模型以追求更精确的散射解释。文献[13]对极化相干矩阵进行方位角补偿来最小化交叉极化分量,形成了Y4R(Yamaguchi four-component decomposition with rotation)算法以改善体散射过估问题。文献[14]考虑FDD所提出的体散射模型不能完全描述实际复杂地物的随机散射过程,根据极化熵理论,引入了一种描述完全随机散射过程的体散射模型,实现了四分量分解方法。文献[15]考虑极化SAR方位向与农作物种植行向不一致时,入射电磁波到地表、农作物的二次散射与一般二次散射的区别,建立了有取向的二面角散射模型。文献[16]提出了一种酉变换,称为螺旋角补偿,在经过方位角补偿和螺旋角补偿后,极化相干矩阵的T23项变为零。文献[17]在假设表面散射和偶次散射为反射对称的前提下,采用非负特征值分解的方法,对体散射功率进行限制以消除负功率。文献[18]从散射模型与极化相干矩阵自适应匹配的角度出发,提出了一种自适应优化的三分量分解方法以解决负功率和散射机制模糊的问题。文献[19]通过分离偶次散射模型和表面散射模型的方位角,使散射模型更一般化,同时采用非线性最小二乘代替传统的求解过程。文献[20]通过研究散射模型的极化对称性,包括反射对称性、旋转对称性和方位对称性,提出了3种基于极化对称性的新散射模型。
除此之外,许多研究倾向于引入新的更为复杂的散射模型。文献[21]通过引入与正交极化散射分量相关的线散射模型,提出了一种五分量极化目标分解方法,可以更好地描述城市中人造建筑的复杂线状散射。受文献[21]中五分量分解思想的启发,文献[22]进一步构建了交叉散射模型,强调了交叉极化散射分量,特别是由大方位角建筑引起的交叉极化散射分量,有利于大方位角建筑物区域的散射提取。文献[23]提出了复合偶极子模型,解释了螺旋散射模型可能的复合偶极子形式,并提出了±45°定向偶极子模型以及±45°定向四分之一波模型,解释了极化相干矩阵中T13的实部和虚部,形成了6SD(Singh six-component scattering decomposition)算法。在此基础上,同样是通过复合偶极子模型,文献[24]提出了新的复合偶极子相干矩阵,以解释T23的实部,并且取消了极化方位角补偿,形成了7SD(Singh seven-component scattering decomposition)算法。在文献[22]提出的交叉散射模型的基础上,文献[25]通过合理分配斜向建筑引起的共极化和交叉极化散射功率,提出了一种斜向二面体散射模型,将6SD扩展为七分量分解。文献[26]在7SD的基础上,利用组合偶极子的方式引入两个散射分量分别对T12实部和虚部解释,提出了九分量分解方法。
上述基于模型的分解方法能够直观有效地解释大多数地物目标极化散射机制,但是目前该领域仍然存在一些问题。一方面,虽然通过采用极化方位角补偿,引入带有交叉极化散射项的散射分量,以及通过其他数学方法优化现有散射模型等方法已经有效地改善了体散射的高估问题,但是大方位角城市建筑区域仍然存在体散射高估和散射机制模糊的问题。文献[19]提出极化方位角补偿处理并不能总是保证偶次散射和表面散射分量同时旋转回零方位角,这说明采用对整个极化相干矩阵进行旋转的方法所建立的散射模型并不能准确地描述地物真实的散射过程。特别是在大方位角城市建筑区域,偶次散射模型与表面散射模型的极化方位角差异巨大,这也就造成了这些区域分解结果与实际散射机制不一致的情况。另一方面,在建立各散射分量模型后,许多学者会将分解过程视为纯粹的数学解算过程,而忽略了物理规律上的限制。例如在早期的分解方法中会出现负功率的现象。虽然之后的算法通常会加入功率限制来直接避免负功率的出现,然而如果未在分解过程中就将系统噪声等物理规律纳入考虑的范畴,计算过程中往往可能导致奇异解,由此得到的分解结果将不再稳定可靠。
为解决上述问题,本文提出一种基于模型的六分量目标分解方法。首先,不同于Y4R等方法采用极化方位角补偿的策略,本文分别分析每个散射分量的旋转不变性,对旋转变化的散射模型,包括偶次散射模型、偶极子模型和四分之一波模型,分别引入不同的极化方位角以描述其方位角,通过这种方式优化后的散射模型更加一般化,能够更准确地描述地物实际的散射过程。然后,本文采用理想平面散射代替Bragg表面散射作为表面散射模型,采用理想的二面角散射器作为偶次散射模型,使得这两个散射分量在解算过程中不再直接联系,同时简化后的表面散射模型和偶次散射模型中T12项为零,极化相干矩阵的T12、T13的实部和虚部由引入极化方位角的广义偶极子模型和广义四分之一波模型解释,总体而言,降低了各个散射分量之间的耦合性,同时整个极化相干矩阵的9个元素被完全利用。最后,在求解各散射分量的功率的过程中,利用T22+T33具有旋转不变性,将T22与T33视为一体计算,避免极化方位角估计得不准确导致的解算误差,同时求解过程也避免了三角函数及除法的参与,分解结果更加稳定可靠。利用GF-3和UAV SAR全极化数据与其他分解方法进行对比试验,试验结果表明,本文方法能够在保证森林植被、海洋水体等自然区域的主导散射正确提取的情况下,有效地改善城市建筑特别是大方位角建筑区域的体散射高估问题,总体分解结果更为符合实际地物散射过程。
1 极化方位角旋转极化SAR系统测量得到极化散射矩阵S,它包含了散射体的信息
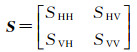 (1)
(1)
式中,下标H和V分别表示水平和垂直极化,SHV代表垂直发射水平接收,假设系统遵循互易原理,交叉极化分量相等,即SHV=SVH,对应的极化相干矩阵〈T〉将降维为3×3。将地面上的散射体视为矢量,当散射体在垂直于雷达视线的平面上绕雷达入射方向逆时针旋转角度θ时,该旋转可以等价于:目标不动,雷达视线顺时针转动角度θ,即坐标系HV顺时针转动角度θ。旋转后的极化散射矩阵S(θ)与S有以下关系
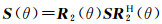 (2)
(2)
式中,旋转矩阵R2(θ)为
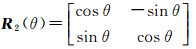 (3)
(3)
对应的极化相干矩阵〈T〉经过旋转后,将变为
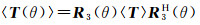 (4)
(4)
式中,旋转矩阵R3(θ)为
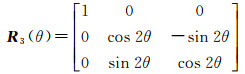 (5)
(5)
易知,为了最小化交叉极化分量的极化方位角补偿方法,是该旋转过程的反过程,极化方位角为θ的S(θ)和〈T(θ)〉经过反向旋转可得到极化方位角为零的S和〈T〉,即
 (6)
(6)
对于多视PolSAR数据,文献[23]提出了基于模型的六分量分解(6SD),认为一个相干矩阵由6种散射分量组成:表面散射、偶次散射、螺旋散射、体散射、±45°定向偶极子及±45°定向四分之一波模型。为了降低体散射高估,其在分解之前对相干矩阵进行了极化方位角补偿。而文献[19]提出极化方位角补偿处理并不能总是保证偶次散射和表面散射分量同时旋转回零方位角,受此启发,本文分别引入了3个极化方位角来描述偶次散射模型、偶极子模型及四分之一波模型,在引入极化方位角后,广义偶极子模型和广义四分之一波模型能够同时解释T12和T13的实部和虚部。为降低分解过程中未知变量的数量,同时有效地解耦表面散射模型和偶次散射模型,本文对表面散射和偶次散射进行了简化处理,Bragg表面散射退化为理想的平面散射,偶次散射退化为理想的二面角散射器[27]。最后,为保证体散射模型的旋转不变性,体散射模型采用经典的均匀分布模型,螺旋散射则采用文献[12]提出的模型。本文所采用的各散射模型如下文所述。
2.1 表面散射模型常用的表面散射模型由粗糙表面的Bragg表面散射现象来表示[27],其极化散射矩阵为
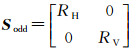 (7)
(7)
对应的相干矩阵为
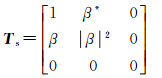 (8)
(8)
式中,β=(RH-RV)/(RH+RV),且β≤1。当RH=RV时,β=0,Bragg表面散射退化为理想平面散射[27],β的物理意义可以看作是粗糙表面对H和V通道极化波反射的差异性度量,此差异性本文将使用旋转偶极子模型表征,由此,表面散射模型简化为
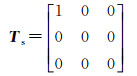 (9)
(9)
简化后的表面散射模型具有旋转不变特性
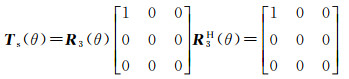 (10)
(10)
通常,偶次散射分量由二面角反射器建模[27],当反射器的表面由不同介电材料构成时,可得到以下的散射矩阵
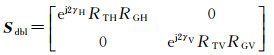 (11)
(11)
式中,下标T和G分别代表垂直面和水平面。通过加入传播因子ej2γH和ej2γV,使得模型更加一般化,其中复系数γH和γV表示任何传播衰减和相变效应,其对应的极化相干矩阵为
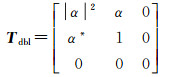 (12)
(12)
式中,α=(RTHRGH+ejϕRTVRGV)/(RTHRGH-ejϕRTVRGV),并且ϕ=2γV-2γH,α是一个复系数,且α≤1。在垂直面和水平面的介电材料近似一致时,偶次散射退化为理想的二面角散射器[27],其不改变水平极化,且使垂直极化方向相反,即散射矩阵有如下的形式
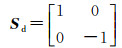 (13)
(13)
对应的极化相干矩阵为
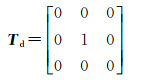 (14)
(14)
显然,二面角散射不具有旋转不变性,且多个文献中提到旋转的二面角将带来显著的交叉散射功率[15, 19-20, 22],本文引入极化方位角θd,其中θd∈-π/2, π/2,来描述二面角绕雷达视线方向旋转的角度,得到改进的偶次散射模型为
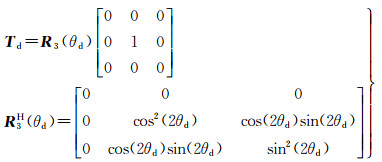 (15)
(15)
比较式(10)和式(15)可知,本文采用的表面散射和偶次散射模型之间不再相互耦合,表面散射分量的功率来自极化相干矩阵的T11,而偶次散射分量的功率来自T22和T33。表面散射模型具有旋转不变性,而改进的偶次散射模型更加强调由于二面角绕雷达视线方向旋转所引起的模型改变,这种改进能够在建模的过程中就有效地解耦这两种散射分量。
由式(15)可知,随着极化方位角θd的变化,偶次散射模型的功率在T22和T33之间转移,当θd=±π/4时,偶次散射模型的功率完全集中于T33,这种改进的偶次散射模型能够更准确地描述极化方位角非零的二面角散射过程。实际的试验数据表明,与小方位角建筑区域相比,大方位角建筑区域的极化相干矩阵中交叉散射项T33更大,本文所提出的偶次散射模型能够有效地描述这种现象,而Y4R等多数分解方法的体散射分量完全由T33决定,这也就导致了体散射高估问题的发生。
2.3 广义偶极子模型水平偶极子的极化散射矩阵为
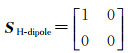 (16)
(16)
对应的Pauli散射矢量为
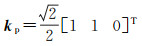 (17)
(17)
其对应的相干矩阵为
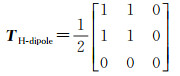 (18)
(18)
同理,垂直偶极子散射模型为
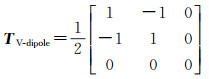 (19)
(19)
粗糙表面的散射矩阵可以分解为RH=RV的表面散射与水平偶极子或垂直偶极子的组合,水平偶极子和垂直偶极子可以看作是描述表面散射中粗糙表面对H和V通道电磁波反射强度的差异性。显然,偶极子散射模型不具有旋转不变性,因此引入极化方位角θod,其中下标od表示带方向的偶极子(oriented dipole), 且θod∈-π/2, π/2,来描述绕雷达视线方向旋转θod角度的偶极子,由式(4)可知,一个水平偶极子经过旋转之后,能得到以下的相干散射矩阵
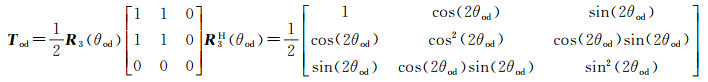 (20)
(20)
式(20)描述的广义偶极子模型较6SD中的±45°定向偶极子模型更具一般性:一方面,在描述自然界中的定向偶极子体,如房屋的棱、铁路与桥梁等拥有锐利的边缘的地物[28],±45°定向偶极子模型仅能描述方位角为±45°的散射体,而广义偶极子模型并未限定方位角因此更具一般性;另一方面,广义偶极子模型还表征了粗糙表面对H和V通道电磁波反射强度的差异性,这是±45°定向偶极子模型所不具备的性质。最后,±45°定向偶极子模型仅解释了T13的实部,而广义偶极子模型解释了T12和T13的实部。
2.4 广义四分之一波模型根据6SD中提及的复合偶极子模型,假设两个正交的偶极子的间距d为λ/8或3λ/8,如图 1所示,这种复合偶极子的散射矩阵模型可以表征为
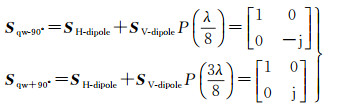 (21)
(21)
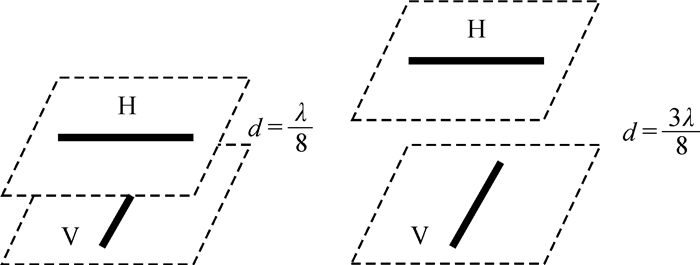
|
| 图 1 四分之一波反射器偶极子构型 Fig. 1 Dipole configurations quarter-wave reflector |
这种四分之一波反射器模型对应的极化相干矩阵分别为
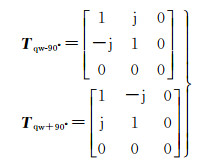 (22)
(22)
上述的复合偶极子模型显然不具备旋转不变性,因此,对-90°相位的四分之一波模型引入极化方位角θq,其中,下标q表示四分之一波(quarter wave)反射器,且θq∈-π/2, π/2,以描述复合偶极子绕雷达视线方向旋转的情形,得到极化相干矩阵为
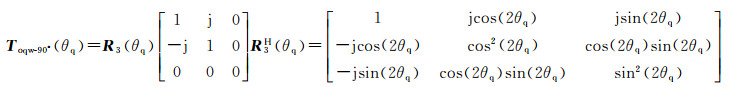 (23)
(23)
当θq=±π/2时,容易发现,-90°相位的四分之一波模型与+90°模型的四分之一模型等价
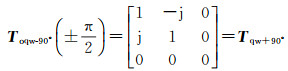 (24)
(24)
因此,广义四分之一波模型可以仅由-90°相位的四分之一波模型旋转而统一描述
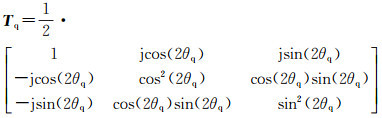 (25)
(25)
广义四分之一波模型较6SD提出的±45°定向四分之一波模型更具一般性:一方面,在描述自然界中的正交偶极子体[28],广义四分之一波模型不再限制复合偶极子的方位角;另一方面,广义四分之一波模型是偶次散射的一种特殊情况,可以描述偶次散射模型中两个散射面的差异性。最后,±45°定向四分之一波模型仅解释了极化相干矩阵T13的虚部,而广义四分之一波模型解释了极化相干矩阵T12和T13的虚部。
2.5 体散射模型和螺旋散射模型为保证体散射模型的旋转不变性,且降低由于体散射模型不同导致分解结果的差异,本文的体散射模型采用经典的FDD体散射模型,该模型假设偶极子在-π, π的范围内均匀分布,因此具有旋转不变性
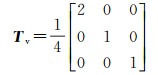 (26)
(26)
螺旋散射首次由Y4O引入[12],其相干矩阵为
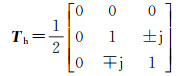 (27)
(27)
易知,该相干矩阵具有旋转不变性
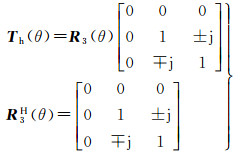 (28)
(28)
本文将极化相干矩阵分解为体散射分量、表面散射分量、螺旋散射分量、改进的偶次散射分量、广义偶极子分量及广义四分之一波分量6部分,这些散射分量在上一节给出了详细推导过程,具体如式(9)、式(15)、式(20)、式(25)—式(27)所示,至此本文提出的分解框架可以表示成如下形式
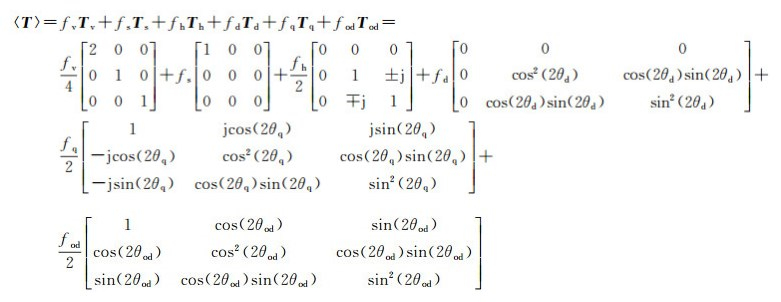 (29)
(29)
式中,待确定的系数一共有9个:fv、fs、fh、fd、θd、fq、θq、fod、θod,同时得到了9个方程
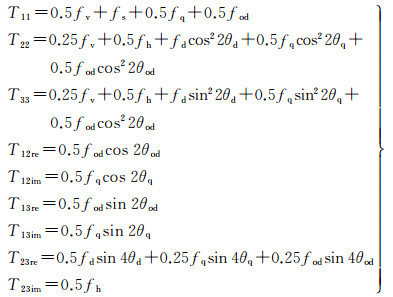 (30)
(30)
由式(30)容易解得fh、fq、θq、fod、θod
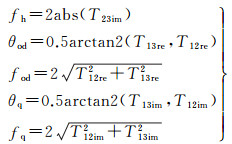 (31)
(31)
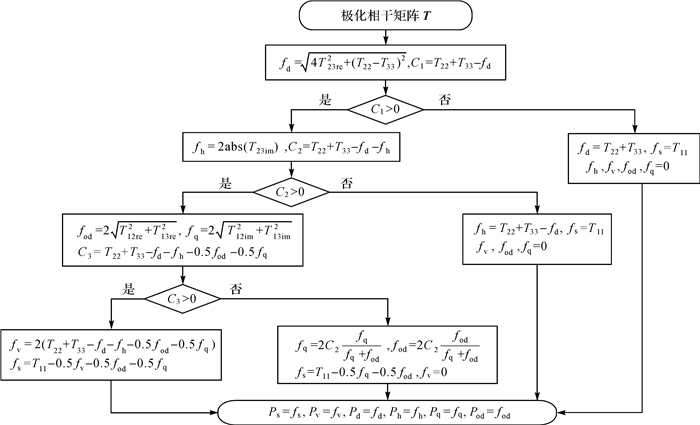
若使用式(31)直接求解得到fh、fq、θq、fod、θod,将可能使T′=T-fiTi(i=h, od, q)的主对角线元素为负[20],此时T′不再是一个具有物理意义的极化相干矩阵。为了避免这种情况的出现,本文每次计算出的分量功率被设定为最大可能值,并利用T22+T33的剩余功率确定该分量功率是否可以达到最大值,具体如图 2所示。
|
| 图 2 本文提出的极化相干矩阵六分量分解方法 Fig. 2 Proposed six-component decomposition method of polarization coherence matrix |
为首先提取出偶次散射分量,假设fq, fod为小量,得到偶次散射分量最大值为
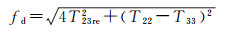 (32)
(32)
由于偶次散射分量fd不应超过T22+T33,根据剩余能量C1=T22+T33-fd的正负,进入第一个分支判断,以确定fd的值。并且螺旋散射分量最大值为
 (33)
(33)
同样地,偶次散射分量与螺旋散射分量之和fd+fh不应超过T22+T33,因此根据C2=T22+T33-fd-fh的正负以确定fh的值。并根据式(31)分别得到fq, fod最大值分别为
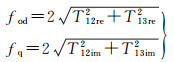 (34)
(34)
与前文相同,利用判别条件C3=T22+T33-fd-fh-0.5fod-0.5fq防止求解出的分量能量超过T22与T33之和,从而确定fq、fod的值。最后,fv可以根据T22+T33的剩余功率求得,fs的值可以根据T11的剩余功率求得,整个6分量分解过程结束。
容易发现,有别于其他分解方法,本文在对各分量功率进行分解的过程中,将T22与T33视为一体计算,这种处理方法能够有效地避免极化方位角估计的不准确导致的解算误差。由式(4)可知,经过旋转后的极化相干矩阵的元素之间有以下关系
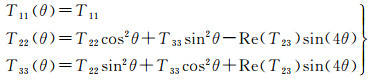 (35)
(35)
由式(35)可以发现以下规律:极化相干矩阵的总功率T11+T22+T33具有旋转不变性;极化相干矩阵的T11具有旋转不变性;随着极化方位角的变化,功率在T22与T33之间转移,但是T22+T33作为一个整体具有旋转不变性。利用这些规律,将T22与T33作为整体考虑,极化方位角将并不直接代入计算过程中,而是直接被消元,计算得到的各分量功率更加稳定。由于极化方位角在计算的时候被消元,因此本文后续不再针对这3个极化方位角的计算结果进行详细的分析。
本文方法的另一个优势是分解过程中不存在除一个小量的计算,这一点在多数分解方法中往往被忽视。例如,在FDD算法中,求解参数α和β采用除法计算,这导致求解出两个参数可能不满足0≤α≤1, 0≤β≤1这一建模时的假设;在Y4R算法中,在T11≈2T33时,使用除法求解出来的表面散射和二次散射功率将不稳定,而试验过程中发现除了森林区域之外,45°城市建筑区域中也存在T11≈2T33的情况,由此导致Y4R方法对大方位角城市建筑区域的散射机制描述并不准确,与Y4R一脉相承的6SD与7SD等方法存在相同的情况;其他的算法,如文献[21]提出的MCSM方法,文献[22]提出的交叉散射模型等,在分解的过程中都存在除法操作,且这些算法都未考虑由于系统噪声导致除数为小量时的特殊处理。本文方法在分量功率解算过程中,一旦某个分量功率被求解出来,则将该分量从相干矩阵的主对角线中减去,在这个过程中,始终保证主对角线元素非负,同时整个过程没有除一个小量的计算,因此分解结果不会产生异常解,得到的结果更加可靠。
4 试验和分析 4.1 GF-3全极化数据试验结果本节首先采用成像位置位于美国加利福尼亚州旧金山湾的GF-3 C波段全极化SAR数据以验证所提分解方法的性能。该数据采集时间为2017年9月,其方位向和距离向分辨率为8 m,图像大小为2529×7173像素,地物类型主要包括海洋水体、不同方位角的城区建筑物和森林区域等典型地物,利用Y4R[13]、6SD[23]和7SD[24]作为对比方法,试验结果如图 3所示,其中红色表示偶次散射分量,绿色表示体散射分量,蓝色表示表面散射分量。为更清晰直观地验证本文分解方法的有效性,截取并放大图 3(d)中方框区域E,该区域由方向多样的建筑物群落及少量的植被区域构成,建筑物方向大多与雷达视线方向不平行。图 4显示了区域E在4种算法下的分解结果以及对应的光学卫星图像,容易发现,相比于其他3种方法的分解结果,本文方法的分解结果中城市建筑区域体散射分量剧烈减弱,偶次散射得到显著增强,由此可见,在城市建筑区域本文方法对于偶次散射分量的提取比其他3种分解方法更加充分,能够有效地改善这些区域体散射高估的问题。

|
| 图 3 不同方法在旧金山湾地区高分3号C波段全极化数据极化分解伪彩色图 Fig. 3 Polarization decomposition pseudo-color image of GF-3 C-band full-polarization data in San Francisco Bay Area by different methods |

|
| 图 4 区域E 4种分解方法结果对比与该区域光学卫星图像 Fig. 4 Comparison of the results of the four decomposition methods of region E and the optical satellite images of the region |
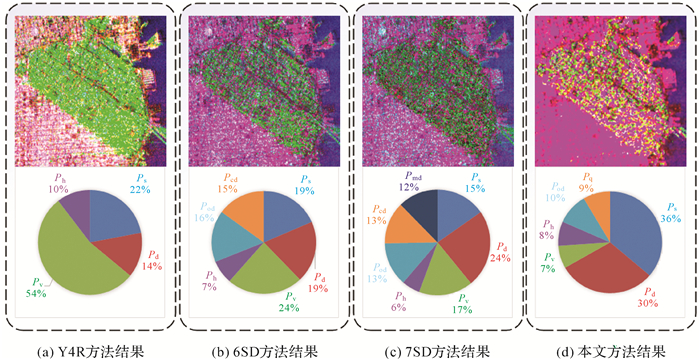
为定量的验证本文分解方法性能,选取了如图 3(d)圆圈圈出的4块典型地物区域:丘陵地形上的植被区域A;海洋水体区域B;小方位角城市建筑区域C;大方位角城市建筑区域D,并在每个区域提取出一个80×80的小块统计各分量比例。区域B、C和D的统计结果分别见表 1—表 3,图 5显示了大方位角城市建筑区域A的分解结果放大图及各分量占比饼状图。
| 散射分量功率 | Y4R | 6SD | 7SD | 本文方法 |
| Ps | 30.97 | 25.04 | 21.12 | 22.55 |
| Pd | 10.96 | 18.12 | 17.11 | 9.16 |
| Pv | 47.70 | 30.93 | 34.90 | 37.11 |
| Ph | 10.36 | 6.50 | 5.35 | 4.87 |
| Pod | - | 9.79 | 7.92 | 13.09 |
| Pq/Pcd | - | 9.62 | 8.23 | 13.22 |
| Pmd | - | - | 5.37 | - |
| 散射分量功率 | Y4R | 6SD | 7SD | 本文方法 |
| Ps | 98.42 | 97.23 | 98.58 | 97.76 |
| Pd | 0.75 | 0.72 | 0.38 | 1.38 |
| Pv | 0.55 | 0.89 | 1.04 | 0 |
| Ph | 0.28 | 0.39 | 0 | 0.12 |
| Pod | - | 0.39 | 0 | 0.38 |
| Pq/Pcd | - | 0.39 | 0 | 0.37 |
| Pmd | - | - | 0 | - |
| 散射分量功率 | Y4R | 6SD | 7SD | 本文方法 |
| Ps | 55.73 | 52.52 | 51.69 | 53.70 |
| Pd | 40.64 | 42.63 | 42.24 | 41.17 |
| Pv | 2.95 | 3.16 | 3.85 | 0.03 |
| Ph | 0.68 | 0.66 | 0.49 | 1.71 |
| Pod | - | 0.46 | 0.27 | 2.24 |
| Pq/Pcd | - | 0.57 | 0.33 | 1.15 |
| Pmd | - | - | 1.14 | - |
|
| 图 5 大方位角城市建筑区域分解结果及对应分量饼状图 Fig. 5 Decomposition results of urban building areas with large orientation angles and pie chart of corresponding components |
由表 1可知,对于丘陵地形上的植被区域A,本文方法的体散射分量占比高于6SD和7SD方法,说明本文方法对植被区域的体散射提取更加充分,由图 3可知,在植被区域本文方法的结果图中绿色分量比6SD和7SD更强。表 2展示了4种方法在海洋水体区域B的分解结果,4种方法的分解结果基本相同,表面散射占据绝对主导,结果符合水体区域散射过程。小方位角城市建筑区域的分解结果见表 3,4种方法的分解结果几乎一致,主导散射来自于建筑物墙壁与地表构成的偶次散射及来自地表或屋顶的表面散射,由于统计的小块中并没有树木,因此体散射功率占比都很低,需要指出的是,本文方法的体散射占比仅为0.03%,优于其他3种方法。
图 5显示了图 3(d)中圆圈圈出的区域D的分解结果放大图及其各分量占比饼状图。容易发现,从左往右,体散射分量占比依次降低,本文方法的体散射占比由7SD中的17%降低至7%,降低幅度为59%,有效地解决了大方位角建筑区域体散射高估的问题。同时,增强了对该区域主导散射即表面散射和偶次散射的提取,表面散射和偶次散射之和由7SD中的39%提升至66%,提升幅度为69%。同时还容易发现,在其他3种方法的分解结果中,Y4R的体散射被高估为主导散射,而6SD和7SD方法的分解结果中各种散射分量的占比接近,主导散射类型模糊,而本文方法能清楚地分辨出主导散射为偶次散射和表面散射,因此本文方法对实际地物散射特征的提取更加准确,结果更符合该地区的实际散射特征。
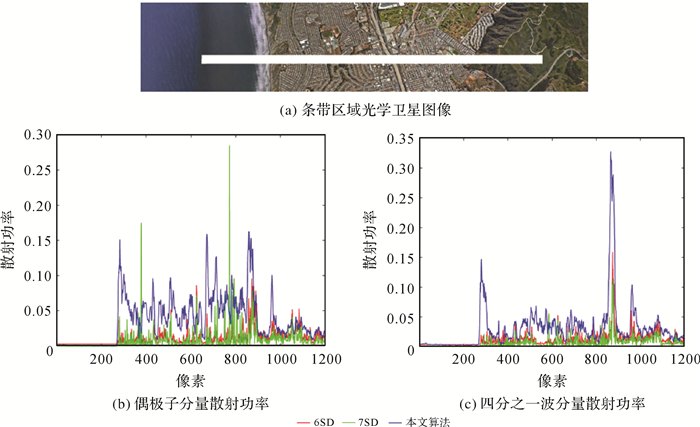
为了比较6SD、7SD与本文所提出的广义偶极子模型和广义四分之一波模型的性能,在如图 3(d)的中部选取了一个40×1200像素的条带,该条带从左到右的地物依次为海洋水体、方向各异的建筑物群落及树木植被,图 6给出了该条带区域3种方法的偶极子分量和四分之一波分量的变化情况。由图 6(b)可知,本文提出的广义偶极子散射分量多出现于城市建筑物区域,并明显高于其他两种方法,这证明了前文提到的广义偶极子模型能够描述自然界中如房屋的棱、铁路或桥梁等含有锐利边缘的地物,而树木枝干也有可能产生这种散射,因此植被区域也含有一定的广义偶极子功率。由图 6(c)可知,本文所提出的广义四分之一波散射分量的散射功率明显高于其他两种方法,由文献[28]可知,两个正交的偶极子能够产生四分之一波散射分量,由于本文所提出的改进模型不再限制正交偶极子对的方向,因此本文方法能够更加充分的提取该分量。
|
| 图 6 偶极子分量和四分之一波分量在条带区域的分布 Fig. 6 Distribution of dipole and quarter wave components in the band region |
4.2 UAV SAR全极化数据试验结果
不失一般性,本文采用成像位置位于美国路易斯安那州南部新奥尔良市的UAV SARL波段全极化数据验证本文方法,该数据采集时间为2015年5月,其方位向分辨率为7.3 m,距离向分辨率为6.7 m,图像尺寸为3300×19 051像素,地物类型主要包括不同方位角的城市建筑群、海洋水体及植被区域。由于图像尺寸较大,本文首先选取数据中包含不同方位角城市建筑群的部分(3300×1500像素)进行试验,以验证本文方法对于不同方位角城市建筑区域体散射高估问题的改善效果,数据在Y4R、6SD、7SD及本文方法下的分解结果如图 7所示,其中红色表示偶次散射分量,绿色表示体散射分量,蓝色表示表面散射分量,可以发现本文方法对偶次散射的提取最为充分,对大方位角城市建筑区域体散射高估问题的改善十分明显。选取如图 7(e)圈出的3个城市建筑区域进行定量分析,容易发现由A到C方位角大小依次增加,各区域散射分量占比见表 4—表 6。

|
| 图 7 不同方法在UAV SARL波段全极化数据上的分解结果 Fig. 7 Decomposition results of different methods on UAV SAR L-band fully polarized data |
| 散射分量功率 | Y4R | 6SD | 7SD | 本文方法 |
| Ps | 30.27 | 29.15 | 29.81 | 38.70 |
| Pd | 60.22 | 63.05 | 62.05 | 51.47 |
| Pv | 7.59 | 3.17 | 3.41 | 0.30 |
| Ph | 1.93 | 1.18 | 1.32 | 2.93 |
| Pod | - | 0.94 | 0.70 | 4.47 |
| Pq/Pcd | - | 2.50 | 1.71 | 2.11 |
| Pmd | - | - | 1.00 | - |
| 散射分量功率 | Y4R | 6SD | 7SD | 本文方法 |
| Ps | 29.92 | 29.79 | 30.56 | 37.06 |
| Pd | 56.62 | 59.72 | 57.64 | 49.14 |
| Pv | 10.87 | 4.20 | 4.63 | 0.66 |
| Ph | 2.59 | 2.40 | 1.30 | 3.68 |
| Pod | - | 1.61 | 1.22 | 6.07 |
| Pq/Pcd | - | 2.27 | 1.34 | 3.39 |
| Pmd | - | - | 3.32 | - |
| 散射分量功率 | Y4R | 6SD | 7SD | 本文方法 |
| Ps | 36.48 | 36.49 | 35.05 | 37.65 |
| Pd | 32.52 | 36.75 | 33.48 | 32.28 |
| Pv | 26.16 | 16.05 | 19.94 | 6.68 |
| Ph | 4.85 | 4.00 | 2.52 | 5.58 |
| Pod | - | 3.26 | 2.25 | 10.44 |
| Pq/Pcd | - | 3.44 | 2.25 | 7.36 |
| Pmd | - | - | 4.50 | - |
由表 4—表 6可知,随着方位角的增加,4种方法的偶次散射分量占比都有所降低,而体散射分量占比则大幅度提高,而本文方法的体散射占比在4种方法中是最低的,特别是在体散射明显出现高估的C区域,较之6SD方法的16.05%,本文体散射分量占比仅为6.68%,降低幅度为58%,这说明本文方法有效地改善了由于方位角增加引起的体散射高估问题。同时还可以发现,随着方位角的增加,本文提出的广义偶极子散射分量和广义四分之一波散射分量幅度明显增加,而6SD和7SD提升幅度很小,这表示本文所提出的这两种改进的散射模型,能更好地描述大方向角城市建筑区域的散射特征。
为验证本文方法能够在解决大方位角建筑区域的体散射高估问题的同时,能够有效地保持森林区域的体散射分量的提取,本文还对该数据的另一森林区域(800×800像素)进行了定量分析,试验结果如图 8所示,其中红色表示偶次散射分量,绿色表示体散射分量,蓝色表示表面散射分量,选取如图 8(e)中白色矩形框框出的区域作定量分析,结果见表 7,可以发现在4种方法中,本文方法体散射分量占比高于6SD和7SD方法,说明本文方法能够充分地提取森林植被区域的主导散射分量,分解结果符合该区域实际的散射过程。

|
| 图 8 不同方法在UAV SARL波段植被区域上的分解结果 Fig. 8 Decomposition results of different methods on UAV SAR L-band vegetation region data |
| 散射分量功率 | Y4R | 6SD | 7SD | 本文方法 |
| Ps | 31.19 | 34.64 | 36.84 | 27.92 |
| Pd | 22.72 | 27.37 | 26.46 | 23.59 |
| Pv | 43.25 | 26.91 | 23.21 | 30.29 |
| Ph | 2.84 | 2.75 | 2.57 | 1.44 |
| Pod | - | 4.48 | 4.47 | 12.24 |
| Pq/Pcd | - | 3.85 | 3.62 | 4.50 |
| Pmd | - | - | 2.83 | - |
5 结束语
本文提出了一种改进的基于模型的六分量极化目标分解方法。本文首先对极化相干矩阵以及极化方位角的定义进行了介绍,然后分析了对整个极化相干矩阵进行极化方位角补偿的方式,不能使所有散射分量同时旋转回零方位角,因此引入了3个独立极化方位角对偶次散射模型、偶极子模型和四分之一波模型分别描述,得到了更一般的广义偶极子模型、广义四分之一波模型及改进的偶极子模型。本文对表面散射模型和偶次散射模型进行了简化和改进,简化改进后的表面散射模型具有旋转不变性,而偶次散射模型更加强调由于二面角绕雷达视线方向旋转所引起的模型改变,实现了表面散射模型和偶次散射模型数学上的解耦,同时减少了未知参数的数量。本文所采用的6个模型共9个自由度,完全利用了极化相干矩阵的9个元素,更好地利用了极化相干矩阵的信息。通过分析极化相干矩阵主对角线元素的旋转不变性,并利用该性质避免了极化方位角参与计算,一定程度解耦了各散射分量,同时分析了求解过程中由于除法引起解的不稳定,并在设计分解方法的时候有效地规避了该问题,因此所得到的解更加稳定可靠。利用GF-3和UAV SAR全极化数据进行试验,试验结果表明,较现有的分解方法,本文方法有效降低了城市建筑特别是大方位角建筑区域的体散射高估现象,增强了建筑区域的主导散射即表面散射和偶次散射的提取,同时也能够保证森林植被、海洋水体等自然区域的主导散射正常提取,总体分解结果更为符合实际地物散射过程。
| [1] |
张腊梅, 段宝龙, 邹斌. 极化SAR图像目标分解方法的研究进展[J]. 电子与信息学报, 2016, 38(12): 3289-3297. ZHANG Lamei, DUAN Baolong, ZOU Bin. Research development on target decomposition method of polarimetric SAR image[J]. Journal of Electronics & Information Technology, 2016, 38(12): 3289-3297. |
| [2] |
XIANG Deliang, TANG Tao, HU Canbin, et al. Built-up area extraction from PolSAR imagery with model-based decomposition and polarimetric coherence[J]. Remote Sensing, 2016, 8(8): 685. DOI:10.3390/rs8080685 |
| [3] |
XIANG Deliang, BAN Yifang, SU Yi. The cross-scattering component of polarimetric SAR in urban areas and its application to model-based scattering decomposition[J]. International Journal of Remote Sensing, 2016, 37(16): 3729-3752. DOI:10.1080/01431161.2016.1201235 |
| [4] |
刘修国, 姜萍, 陈启浩, 等. 利用改进三分量分解与Wishart分类的极化SAR图像建筑提取方法[J]. 测绘学报, 2015, 44(2): 206-213. LIU Xiuguo, JIANG Ping, CHEN Qihao, et al. Buildings extraction from polarimetric SAR image using improved three-component decomposition and wishart classification[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(2): 206-213. |
| [5] |
CHEN Siwei, SATO M. Tsunami damage investigation of built-up areas using multitemporal spaceborne full polarimetric SAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(4): 1985-1997. DOI:10.1109/TGRS.2012.2210050 |
| [6] |
ANTROPOV O, RAUSTE Y, HAME T. Volume scattering modeling in PolSAR decompositions: study of ALOS PALSAR data over boreal forest[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10): 3838-3848. DOI:10.1109/TGRS.2011.2138146 |
| [7] |
付海强, 汪长城, 朱建军, 等. Neumann分解理论在极化SAR植被分类中的应用[J]. 武汉大学学报(信息科学版), 2015, 40(5): 607-611. FU Haiqiang, WANG Changcheng, ZHU Jianjun, et al. A polarimetric classification method based on Neumann decomposition[J]. Geomatics and Information Science of Wuhan University, 2015, 40(5): 607-611. |
| [8] |
张斌, 杨然, 谢兴, 等. 利用极化目标分解和WMRF的全极化SAR图像分类方法[J]. 武汉大学学报(信息科学版), 2011, 36(3): 297-300. ZHANG Bin, YANG Ran, XIE Xing, et al. Classification of fully polarimetric SAR image based on polarimetric target decomposition and wishart Markov random field[J]. Geomatics and Information Science of Wuhan University, 2011, 36(3): 297-300. |
| [9] |
郎丰铠, 杨杰, 赵伶俐, 等. 基于Freeman散射熵和各向异性度的极化SAR影像分类算法研究[J]. 测绘学报, 2012, 41(4): 556-562. LANG Fengkai, YANG Jie, ZHAO Lingli, et al. Polarimetric SAR data classification with freeman entropy and anisotropy analysis[J]. Acta Geodaeticaet Cartographica Sinica, 2012, 41(4): 556-562. |
| [10] |
ZHAO Yi, JIANG Mi, MA Zhangfeng. Integration of SAR polarimetric features and multi-spectral data for object-based land cover classification[J]. Journal of Geodesy and Geoinformation Science, 2019, 2(4): 64-72. |
| [11] |
FREEMAN A, DURDEN S L. A three-component scattering model for polarimetric SAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(3): 963-973. DOI:10.1109/36.673687 |
| [12] |
YAMAGUCHI Y, MORIYAMA T, ISHIDO M, et al. Four-component scattering model for polarimetric SAR image decomposition[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(8): 1699-1706. DOI:10.1109/TGRS.2005.852084 |
| [13] |
YAMAGUCHI Y, SATO A, BOERNER W M, et al. Four-component scattering power decomposition with rotation of coherency matrix[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(6): 2251-2258. DOI:10.1109/TGRS.2010.2099124 |
| [14] |
殷君君, 安文韬, 杨健, 等. 一种改进的极化SAR图像四成分分解方法[J]. 信息与电子工程, 2011, 9(2): 127-132. YIN Junjun, AN Wentao, YANG Jian, et al. A modified four-component model-based scattering decomposition method of polarimetric SAR images[J]. Information and Electronic Engineering, 2011, 9(2): 127-132. |
| [15] |
闫剑, 李洋, 尹嫱, 等. 引入有取向二面角散射的Freeman-Durden分解[J]. 雷达学报, 2014, 3(5): 574-582. YAN Jian, LI Yang, YIN Qiang, et al. Freeman-durden decomposition with oriented dihedralscattering[J]. Journal of Radars, 2014, 3(5): 574-582. |
| [16] |
AN Wentao, XIE Chunhua, LIN Mingsen. A three-component decomposition algorithm for polarimetric SAR with the helix angle compensation[C]//Proceedings of 2016 IEEE International Geoscience and Remote Sensing Symposium. Beijing: IEEE, 2016: 7501-7504.
|
| [17] |
VAN ZYL J J, ARII M, KIM Y. Model-based decomposition of polarimetric SAR covariance matrices constrained for nonnegative eigenvalues[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(9): 3452-3459. DOI:10.1109/TGRS.2011.2128325 |
| [18] |
蔡永俊, 张祥坤, 姜景山. 极化SAR自适应三分量分解方法[J]. 测绘学报, 2016, 45(9): 1089-1095. CAI Yongjun, ZHANG Xiangkun, JIANG Jingshan. Adaptive three-component decomposition approach for polarimetric SAR data[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(9): 1089-1095. DOI:10.11947/j.AGCS.2016.20150533 |
| [19] |
CHEN Siwei, WANG Xuesong, XIAO Shunping, et al. General polarimetric model-based decomposition for coherency matrix[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(3): 1843-1855. DOI:10.1109/TGRS.2013.2255615 |
| [20] |
AN Wentao, LIN Mingsen. An incoherent decomposition algorithm based on polarimetric symmetry for multilook polarimetric SAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(4): 2383-2397. DOI:10.1109/TGRS.2019.2948683 |
| [21] |
ZHANG Lamei, ZOU Bin, CAI Hongjun, et al. Multiple-component scattering model for polarimetric SAR image decomposition[J]. IEEE Geoscience and Remote Sensing Letters, 2008, 5(4): 603-607. DOI:10.1109/LGRS.2008.2000795 |
| [22] |
XIANG Deliang, BAN Yifang, SU Yi. Model-based decomposition with cross scattering for polarimetric SAR urban areas[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(12): 2496-2500. DOI:10.1109/LGRS.2015.2487450 |
| [23] |
SINGH G, YAMAGUCHI Y. Model-based six-component scattering matrix power decomposition[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(10): 5687-5704. DOI:10.1109/TGRS.2018.2824322 |
| [24] |
SINGH G, MALIK R, MOHANTY S, et al. Seven-component scattering power decomposition of PolSAR coherency matrix[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(11): 8371-8382. DOI:10.1109/TGRS.2019.2920762 |
| [25] |
FAN Hui, QUAN Sinong, DAI Dahai, et al. Seven-component model-based decomposition for PolSAR data with sophisticated scattering models[J]. Remote Sensing, 2019, 11(23): 2802. DOI:10.3390/rs11232802 |
| [26] |
MALIK R, SINGH G, MOHANTY S, et al. Nine component scattering power decomposition of PolSAR data[C]//Proceedings of 2021 European Conference on Synthetic Aperture Radar. [S. l. ]: VDE, 2021: 1-3.
|
| [27] |
LEE J S, POTTIER E. Polarimetric radar imaging: from basics to applications[M]. Boca Raton: CRC Press, 2017: 92-98, 200-213.
|
| [28] |
SINGH G, MOHANTY S, YAMAZAKI Y, et al. Physical scattering interpretation of PolSAR coherency matrix by using compound scattering phenomenon[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(4): 2541-2556. DOI:10.1109/TGRS.2019.2952240 |



