2. 中国地质大学(武汉)地质探测与评估教育部重点实验室, 湖北 武汉 430074;
3. 武汉大学卫星导航定位技术研究中心, 湖北 武汉 430079
2. Key Laboratory of Geological Survey and Evaluation of Ministry Education, China University of Geosciences, Wuhan 430074, China;
3. GNSS Research Center, Wuhan University, Wuhan 430079, China
20多年来,中国大陆构造环境监测网络(Crustal Movement Observation Network of China, CMONOC, 简称“陆态网”)测站累积了大量的GNSS观测文件,通过GNSS精密数据处理,得到测站长时期的坐标时间序列,为大地测量学、地球动力学等学科的研究提供了有效的数据保障[1-3]。GNSS坐标时间序列一般包含了由地壳运动造成的长期线性变化,同时也包含各类空间尺度的地球物理效应(如大气、水文、潮汐等)导致的非线性变化,主要表现为测站位置的季节性震荡。此外,测站位置还包含了由于地震、火山活动等构造运动,以及仪器更换等因素引起的阶跃和震后形变。另外,GNSS坐标时间序列还可能含有因数据处理模型建模不完善或错误建模导致的虚假(非线性)变化。
近20年来,国内外学者开展了众多非线性形变来源的研究工作[4-6]。研究表明,通过建立地表负载模型(surface loading model, SLM),并计算GNSS测站位置的弹性形变位移序列,可以有效研究测站位置处的地球物理影响机制。目前,地表负载模型最理想情况下能够解释约50%的测站垂向周年振幅,水平方向则不到20%[7-8]。除了环境负载,GNSS测站还受到热膨胀效应的影响,表现出一种周期性温度变化引起的天线观测墩及其所在基岩的热弹性形变,也被认为是GNSS坐标时间序列非线性信号的来源之一[9-10]。除此之外,区域性的地球物理因素也会导致GNSS测站产生非线性形变。例如,区域内地下水、石油等的开采、地表强降水[11]、高原冻土周期性冻结与消融[12]等。研究表明,我国的GNSS坐标时间序列在水平方向主要以线性运动为主[13-14],而高程方向则表现为明显的季节性振荡,且不同测站的振荡特性并不相同。对于坐标高程分量中的季节性信号,常将其视为年周期信号及其整数阶谐波分量的组合[15-16],并用最小二乘、最大似然估计(maximum likelihood estimation, MLE)等方法估计出常数振幅和相位。这种参数化的谐波模型对于平稳序列是合适的,而对于非平稳的测站,年际间的测站环境变化及其响应存在差异时,不变的振幅和相位就不再适合描述测站的运动特征,这时就需要将季节性信号的振幅和相位视为随时间变化的。
目前,GNSS坐标时间序列分析中常用的时变信号提取方法有小波分解(wavelet decomposition, WD)和经验模态分解(empirical mode decomposition, EMD)[17-19]。研究表明,WD的效果受小波基的选择及分解层数的影响较大,当依靠经验选择不当时,容易使结果出现偏差[20]。相对而言,EMD按照数据自身的时间尺度特征将信号分解为不同的本征模态函数(intrinsic mode functions, IMF),是一种自适应的方法。自文献[21]提出至今,已在大地测量各类数据处理中有了广泛的应用[22-24]。然而研究表明,对于较为复杂的信号,EMD分解过程中往往会出现模态混叠现象[25],造成不同的模态在同一个IMF分量中共存或相同的模态分成了多个频率相近的模态,因而无法根据时间特征尺度有效区分不同模态。
为解决模态混叠问题,文献[26]提出了变分模态分解(variational mode decomposition, VMD),该方法也是一种自适应信号处理方法,该方法假设每个IMF分量是具有不同中心频率的有限带宽,为使得每个IMF的估计带宽之和最小,通过转换解决变分问题,将各IMF解调到相应的基频带,最终提取各个IMF及相应的中心频率。自VMD方法提出以来,在机械故障检测[27-29]、电力负荷预测[30-31]及语音去噪[32-33]等领域广泛应用。但是,变分模态分解的模态个数目前一般是经验值,同时鲜有学者将其应用在GNSS坐标时间序列分析之中[34]。
考虑到CMONOC测站遍布我国大陆,测站所在地的地形地貌、气候、土壤及水文条件等地理环境因素差异巨大,VMD方法在提取测站时变信号中的有效性和普适性需要进行全面分析。本文将利用VMD和MLE两种方法探测CMONOC测站高程时间序列中的时变信号,验证VMD在GNSS坐标时间序列时变信号提取中的效果,这对于更加真实地反映我国GNSS测站的运动特征,进而研究引起测站运动的地球物理起源具有十分重要的意义。
1 理论方法 1.1 GNSS坐标时间序列分析方法GNSS测站坐标时间序列的函数模型表示为[16]
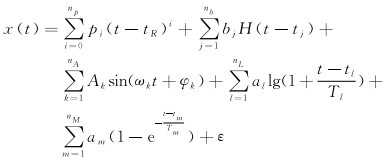 (1)
(1)
式中,x(t)表示GNSS测站坐标时间序列;等式右边第1项表示多项式,系数和阶次为pi和i,对于大多数测站,一阶线性项是由地壳板块运动引起的;第2项表示阶跃,是指测站坐标时序中的突变,H表示Heaviside阶梯函数,bj和tj表示阶跃的大小和发生的时刻;第3项代表周期信号,Ak、ωk和φk分别表示第k个周期信号的振幅、角频率和初相,nA指周期信号的数目;第4、5项用于描述测站的震后形变位移,al、Tl和tl表示对数函数的振幅、弛豫时间和震后形变开始时刻,am、Tm和tm表示指数函数的振幅、弛豫时间和震后形变开始时刻,ε为拟合残差。
在CMONOC测站的数据预处理过程中,已剔除了含有明显阶跃信号和震后形变的测站,因此式(1)中第2、4、5项的影响可暂不予考虑。在常规处理中,多项式项的阶数采用常用的一阶项,而在各类周期信号中,周年和半周年信号最为显著,因此式(1)可简化为
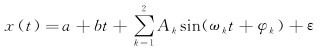 (2)
(2)
式中,a为线性项的截距;b表示线性速度。
1.2 最大似然估计法设单站、单分量GNSS坐标时间序列满足
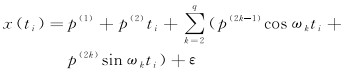 (3)
(3)
式中,p(1)、p(2)分别表示测站的初始坐标和线性速率;q-1为周期信号的数量;p(2k-1)、p(2k)为调和函数的系数,表示周期信号的振幅;ε表示拟合残差。矩阵形式表示为
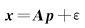 (4)
(4)
若仅考虑周年和半周年信号,则q=3。矩阵x、A和p的具体形式表示为
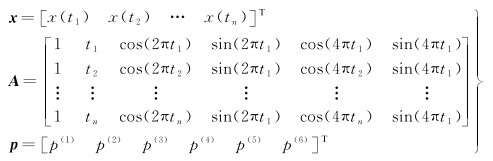 (5)
(5)
假设式(4)中的坐标残差ε是由白噪声α和有色噪声β(t)的线性组合
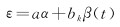 (6)
(6)
式中,系数a、bk分别表示白噪声和有色噪声的振幅大小。通过最小二乘估计法可得到最小二乘解为
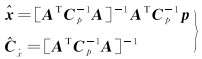 (7)
(7)
协方差矩阵Cp可以表达若干随机噪声过程,如白噪声、可变白噪声、闪烁噪声、随机游走噪声、幂律噪声、一阶高斯马尔可夫噪声,以及它们之间的各类组合。对不同的噪声模型组合,Cp可以表示为不同形式。通过调整Cp使得似然函数取得最大值,即可得到与该时间序列最相近的噪声模型。假设观测值服从高斯正态分布,极大似然函数可表示为
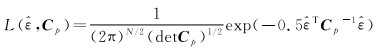 (8)
(8)
式中,det是矩阵的行列式;N为GNSS坐标时间序列的历元数目。按照MLE原理,通过选择不同的噪声模型,使得残差
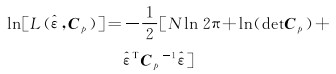 (9)
(9)
MLE可以处理非均匀采样,以及数据缺失较多的时间序列,而且可以同时估计测站的线性速度、周期项、阶跃及噪声振幅等参数。
1.3 变分模态分解不同于EMD方法,在VMD方法中定义IMF为一个调幅调频信号uk(t),其表达式为
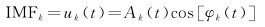 (10)
(10)
式中,Ak(t)为瞬时幅值;φk(t)为瞬时相位,对其求导得瞬时频率ωk(t)
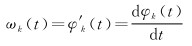 (11)
(11)
VMD算法将变分问题描述为在约束条件为各IMF之和等于输入信号x下寻求k个IMF,使得所有IMF的估计带宽之和最小。具体构造步骤如下。
(1) 对每个分量uk(t)进行Hilbert变换,得到单侧频谱
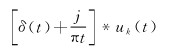 (12)
(12)
(2) 通过加入指数项调整各IMF的中心频率,将各IMF的频谱调制到相应的基频带
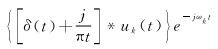 (13)
(13)
(3) 计算上述解调信号梯度的L2范数,估计出各IMF的带宽,假定将原始信号x(t)分解为N个IMF分量,则对应的约束变分模型表达式为
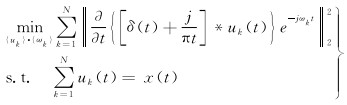 (14)
(14)
式中,∂/∂t表示求偏导;δ(t)为冲激函数;*表示卷积运算;uk={u1, u2, …, uN}代表原始信号x(t)分解得到的N个IMF分量;ωk={ω1, ω2, …, ωN}表示各IMF分量的中心频率。
为求取约束变分模型的最优解,VMD方法通过引入拉格朗日乘子λ(t)和二次惩罚因子α,将待求解的约束性变分问题转变为非约束性变分问题。增广拉格朗日表达式为
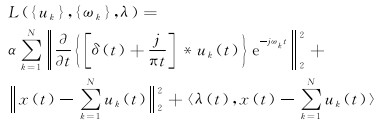 (15)
(15)
式中,〈·〉表示点积运算,各模态分量uk和对应的中心频率ωk采用乘法算子交替方向法求解[35]。
IMF分量个数k的确定在VMD方法中十分重要,k值过小导致模态欠分解,即重构信号的分量个数不足,会影响后续重构过程的精度;k值过大会导致模态重复或产生额外的噪声。在机械故障诊断的应用中,一般选择VMD分量的个数为3~8,利用中心频率观察法确定。首先分别设置k值为3~8依次进行试验,估计不同k值时每个分量的中心频率,标记第一次出现中心频率相近的k值,则确定k-1为分解模态个数。
1.4 时变信号的提取精度为了说明VMD方法提取GNSS坐标时间序列中时变信号的精度,使用RMSE改进率进行判定
 (16)
(16)
式中,RMSEimprove为RMSE的改进率;RMSEreduct1为VMD方法的RMSE减小率;RMSEreduct2为参数化方法求得的RMSE减小率;x表示原始序列;ε表示MLE方法得到的残差序列,与式(2)中含义一致;ξ表示VMD方法得到的残差序列,其中RMSE表达式为
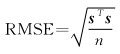 (17)
(17)
式中,s为坐标序列列向量;n为序列的历元数目。RMSEimprove体现了VMD方法相对于MLE方法在降低原始信号RMSE值的有效性方面的差异,值越大,改进效果越好。
除了上述定义的RMSE改进率,还可以利用原始序列x(t)与重构序列
(1) 原始序列与重构序列之间的相关系数ρ表示为
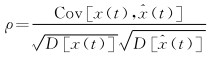 (18)
(18)
式中,Cov[x(t), 



(2) 信噪比SNR的计算公式表示为
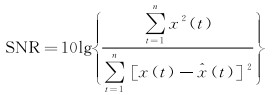 (19)
(19)
SNR主要是体现噪声信号在原始信号中的比重,其值越大,降噪效果越好。
1.5 陆态网高程时间序列本文使用的GNSS坐标时序数据由中国地震局(China Earthquake Administration, CEA)提供,包括所有CMONOC测站的原始的(raw)和去趋势项的(detrend)GNSS坐标时间序列,时间跨度为1999—2019年。中国地震局采用GAMIT/GLOBK10.4软件[38]对所有CMONOC基准站进行了统一解算,得到了基准站的单日松弛解结果,然后经过七参数相似变换将松弛解转换至ITRF参考框架中[30],具体的数据处理策略及说明参考 ftp://ftp.cgps.ac.cn/doc/processing_manual.pdf。GNSS坐标时间序列通常包含了一定量的异常值,以及由于地震或设备更换引起的坐标阶跃,因此应先采用一系列的预处理手段获取相对干净的坐标时间序列。首先,剔除形式误差在水平分量(北向、东向)大于10 mm,同时在高程分量大于20 mm的历元。然后,采用CEA识别出的阶跃值来校正测站坐标时间序列,计算方法是将完整的时间序列在阶跃时刻分为前后两段分别进行函数拟合,前后两段序列在阶跃时刻的估计值之差即为阶跃值。对于某些无法识别的不明原因的阶跃,有必要对测站逐一检查,以避免未扣除的阶跃信号对测站长期趋势和周期项参数估值的不利影响。此外,有些测站还表现出了异常的非线性形变。如果这种异常非线性信号产生的原因是已知的,并且异常仅持续了较短的时间,就简单地剔除测站的异常时间段;如果异常未知并持续时间较长,则删除该站,在下一步的计算分析中不予考虑。在完成数据预处理并删除有效时间跨度少于3 a的测站或存在未知的异常非线性形变的测站之后,剩下的243个CMONOC测站是本文研究的对象。
2 结果与分析在利用VMD对目标信号进行分解的过程中,IMF分量个数的选择至关重要。因此,需要首先讨论IMF分量个数的选取,在此基础上,对IMF分量进行重构,分析VMD方法相较于MLE方法在提取测站时变信号精度方面的差异。对于一些指标的极大、极小值对应的测站,有必要单独进行研究分析。
2.1 IMF分量个数的确定考虑到GNSS测站位置受到多种因素的影响,不仅包含来自卫星端、传播路径、接收端的定位误差,也包含了环境负载效应、热膨胀效应及测站位置相关的局部地球物理因素等。影响GNSS测站位置的信号源众多且存在相互耦合的情况,因此,本文选择VMD分量的个数为3~10,另外惩罚因子α采用默认值1000。确定IMF分量个数一般选择中心频率观察法,具体步骤为:首先,分别设置k=3、4、5、6、7、8、9、10进行试验;然后,估计不同k值时每个分量的中心频率,标记第1次出现中心频率相近的k值;最后,确定k-1为分解模态个数。以测站TJWQ(天津武清)为例,不同k值下(3~10)的中心频率见表 1,单位:次每年(cpy)。
| 模态个数 | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | IMF6 | IMF7 | IMF8 | IMF9 | IMF10 |
| 3 | 0.010 | 99.458 | 164.095 | |||||||
| 4 | 0.010 | 58.860 | 119.457 | 156.694 | ||||||
| 5 | 0.010 | 47.404 | 84.722 | 119.139 | 156.609 | |||||
| 6 | 0.009 | 1.193 | 22.429 | 60.676 | 103.836 | 148.248 | ||||
| 7 | 0.009 | 1.133 | 14.770 | 43.668 | 75.256 | 110.229 | 163.679 | |||
| 8 | 0.009 | 1.188 | 26.701 | 59.203 | 93.111 | 126.408 | 152.657 | 174.474 | ||
| 9 | 0.009 | 1.170 | 26.438 | 55.256 | 80.145 | 108.088 | 133.850 | 156.655 | 174.460 | |
| 10 | 0.009 | 1.147 | 22.718 | 46.826 | 69.606 | 95.628 | 121.705 | 140.696 | 159.550 | 175.375 |
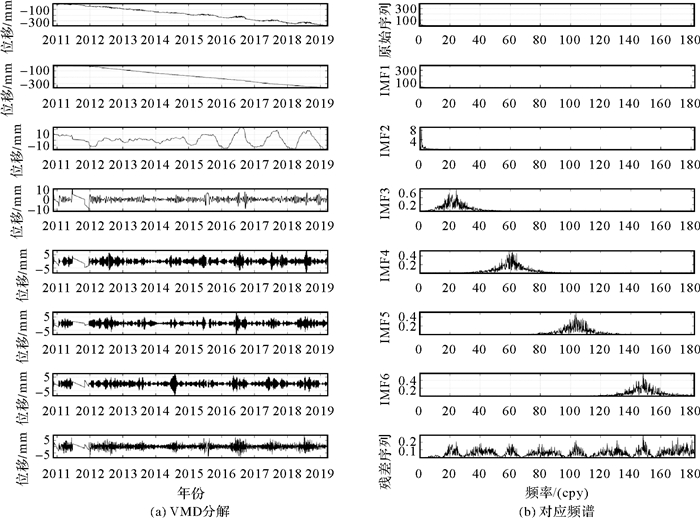
可以看出,对于k值取3~10的过程中,没有出现中心频率相近的模态,因此从避免出现模态混叠的角度看,取IMF分量个数取10是可行的;然而,对于IMF2(主要表现为测站季节性信号),频率约为1 cpy,而k≤5时,并没有出现该频率的模态;k=6时,第一次出现该模态,因此当顾及实际信号的季节性特征,且分解模态数尽可能少的原则,测站TJWQ应该取的模态个数为6。k=6时,该站原始序列、各IMF分量、残差序列及相应的频谱如图 1所示。
|
| 图 1 测站TJWQ高程序列、IMF分量、残差序列及相应的频谱 Fig. 1 Height time series, IMF components, residual series and corresponding power spectrum of station TJWQ |
可以看出,信号分量从IMF1到IMF6由低频到高频变化,IMF1包含了测站的长期线性项,IMF2则反映了测站的季节性运动特征,IMF3—IMF6表示频率更高、频谱强度更弱的某种信号。当选择IMF1和IMF2之和作为重构信号,根据式(16)计算出的RMSE改进率为1.6%。所以,相对于最大似然估计法,VMD具有更优越的减弱测站高程时间序列非线性形变的性能。可见,VMD对复杂信号的处理能力,能够将多分量信号一次性分解成多个单分量调幅调频信号,是一种高效的处理非线性信号的工具。然而,VMD算法本身也存在一些不足之处。对于不同测站,受到的地球物理信号源的影响不同,VMD分解层数也不同。对于CMONOC测站而言,对所有测站逐一使用中心频率观察法进行参数确定任务量较大。同时对于惩罚因子本文采用了常用值,并未给予过多讨论分析。因此,后续研究还需要针对具体测站进行VMD分解层数和惩罚因子的确定,计划采用鲸鱼优化算法(whale optimization algorithm, WOA)自适应确定IMF分量个数。
2.2 CMONOC测站时变信号提取精度VMD分解过程中,IMF分量个数一般选择为3~8。信号重构时选择的IMF分量越多,越能还原出原始信号,与原始信号的相似性就越强,相较于最大似然估计法的RMSE改进率越大,但同时重构信号的组成也会越复杂。因此选择合适的IMF分量至关重要。本节将从RMSE改进率、相关系数和信噪比这3个方面分析VMD方法提取CMONOC测站高程时变信号的精度,重构分量的个数选择3个。
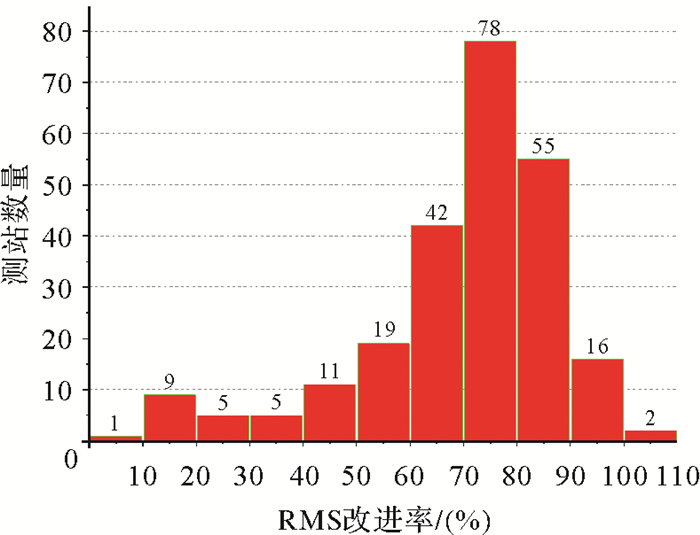
2.2.1 RMSE改进率利用式(9),计算得到VMD方法相对于MLE方法的RMSE改进率,CMONOC测站的RMSE改进率的空间分布与分布直方图如图 2、图 3所示。全部243个测站的RMSE改进率均为正值,表明VMD方法有助于所有测站提取时变信号,减弱高程时间序列中的非线性形变。全部测站RMSE改进率的均值为69.8%,RMSE改进率在60%以上的测站数为193个,占比79.4%,超过100%的测站有2个,分别是YONG(104.6%)和GXBH(100.2%),最低的测站是TJWQ(7.8%)。这些测站将在2.3节中详细分析。RMSE改进率并无明显的地理分布特征。

|
| 图 2 CMONOC测站RMSE改进率空间分布 Fig. 2 Spatial distribution of RMSE improvement rate at CMONOC stations |
|
| 图 3 RMSE改进率分布直方图 Fig. 3 Distribution histogram of RMSE improvement rates |
2.2.2 相关系数
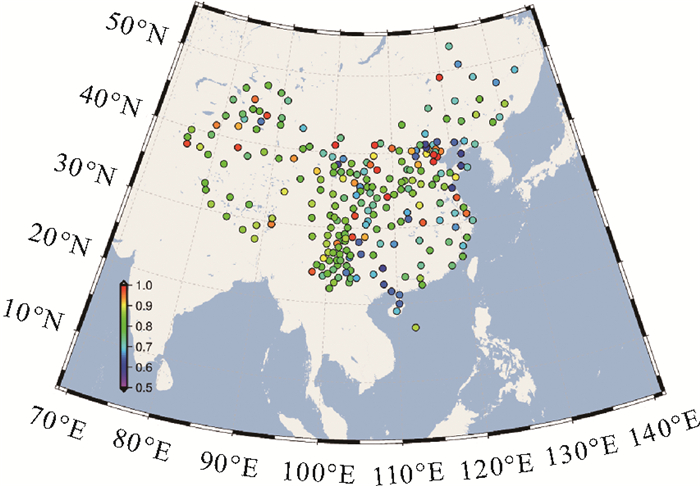
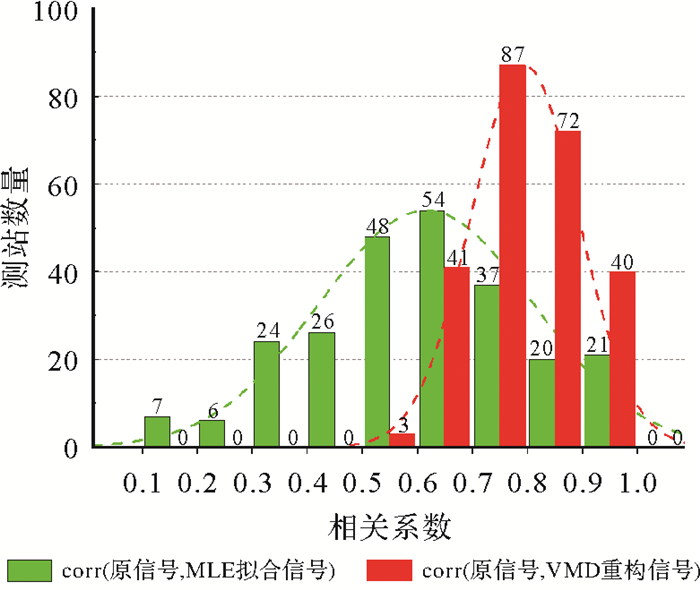
利用式(10),计算得到VMD提取出的重构信号与原始信号之间的相关系数,选取前3个IMF分量进行信号重构时,原始信号与重构信号之间的相关系数达0.99~1,表明原始信号与重构信号的相似度极强,测站的时变信号能够通过VMD方法完美地提取出来。由于所有IMF分量之和即为原始信号,因此重构信号包含的IMF越多,其与原始信号之间的相关性越强。若只选取IMF1进行信号重构时,重构信号与原始信号之间的相关系数降低,此时相关系数超过0.9的测站数为40个。图 4表示CMONOC测站的VMD重构信号与原始信号之间的相关系数,可以看出,这些测站较为均匀地分布在我国大陆,并未表现出明显的地理分布特征。位于天津、河北等沿海地区的测站相关系数较高。相对于VMD方法,MLE方法得到的拟合信号与原始信号之间的相关系数明显较低,全部测站相关系数的均值为0.62,两种方法得到的相关系数分布直方图如图 5所示。
|
| 图 4 CMONOC测站VMD重构信号与原始信号的相关系数空间分布 Fig. 4 Spatial distribution of correlation coefficients between reconstructed signals derived from VMD method and original signals at CMONOC stations |
|
| 图 5 相关系数分布直方图 Fig. 5 Distribution histogram of correlation coefficients |
2.2.3 信噪比
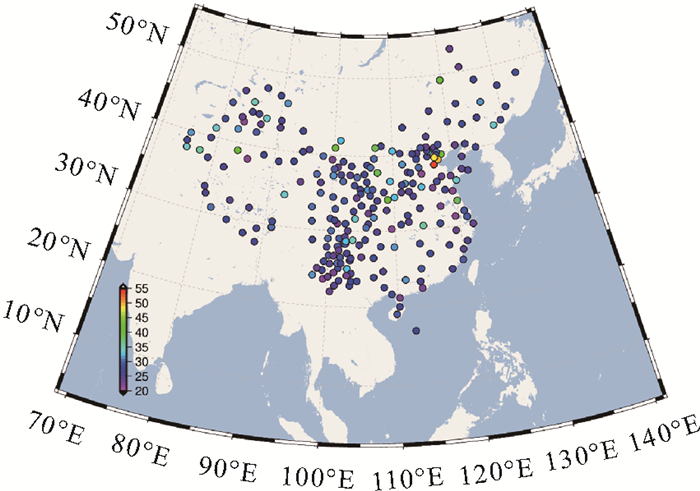
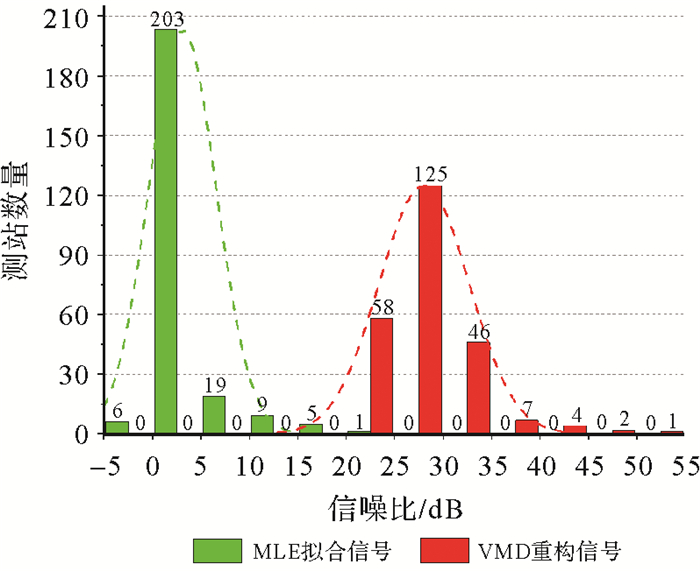
利用式(11),计算得到VMD方法相对于MLE方法的信噪比,信噪比的空间分布与分布直方图如图 6、图 7所示。由式(11)可知,原始信号的信噪比均为0,经过VMD提取出时变信号以后,信噪比提高,全部243个测站的信噪比均值为28.0 dB,有7个测站的信噪比达到40 dB以上,其中信噪比最大的测站是HECX(53.8%)。相对于VMD方法,MLE方法得到的拟合信号的信噪比较低,全部测站的信噪比均值仅为3.1 dB。
|
| 图 6 CMONOC测站VMD方法信噪比空间分布 Fig. 6 Spatial distribution of SNR derived from VMD method at CMONOC stations |
|
| 图 7 信噪比分布直方图 Fig. 7 Distribution histogram of SNR |
2.3 特殊测站分析
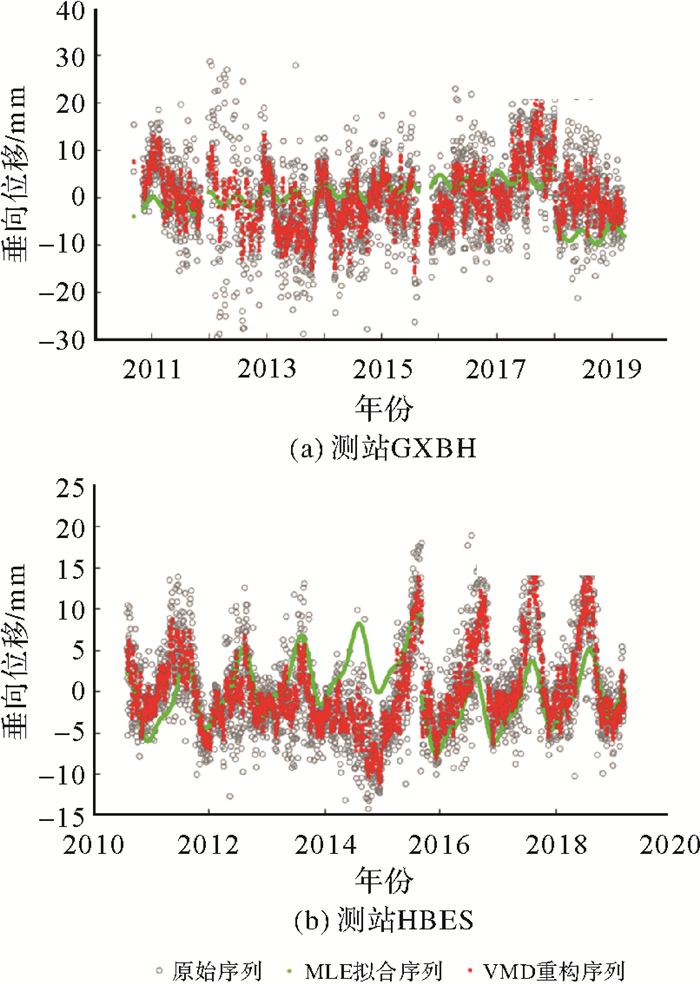
上节提到,全部CMONOC测站中有18个测站的RMSE改进率大于90%,其中测站GXBH、HBES的RMSE改进率分别为100.2%和91.9%,它们的原始信号、MLE拟合信号与VMD重构信号如图 8所示。
|
| 图 8 RMSE改进率大于90%的2个CMONOC测站 Fig. 8 Two CMONOC stations with RMSE improvement rates greater than 90% |
测站GXBH(广西北海)经过VMD方法提取时变信号,RMSE改进率达100.2%。从原始序列可以看出,该站并未表现出明显的季节性信号,即整年周期运动,因此基于“周年+半周年”假设的MLE方法得到的拟合序列并未出现年度振荡(绿点),拟合效果不佳。相对而言,VMD方法首先将原始信号分解为不同中心频率的IMF分量,然后选取前3个IMF分量进行信号重构,重构序列能够较好拟合出原始序列中的高频信号。
测站HBES(湖北恩施)RMSE改进率为91.9%。从原始序列(灰点)可以看出,该测站在2014—2015年间出现一段异于其他年份的下沉现象,VMD方法得到的重构序列可以较好反映这一情况,而MLE方法得到固定的周年振幅和相位,与该时间段内的实际位置变化差异较大。因此,通过VMD方法的分解与重构过程,测站非线性形变可以得到较好的提取。
GNSS坐标时间序列的预处理是一项重要的工作,然而在测站数目众多时,阶跃信号的准确探测和识别会变得相当复杂。对于已知原因的阶跃信号,可以根据地震或仪器更换发生时刻估算阶跃值的大小,进而对原始序列进行改正;对于原因未知或发生时刻难以确定的阶跃信号,目前最有效的方法仍然是人工目视检查[40],但不可避免会出现遗漏情况。
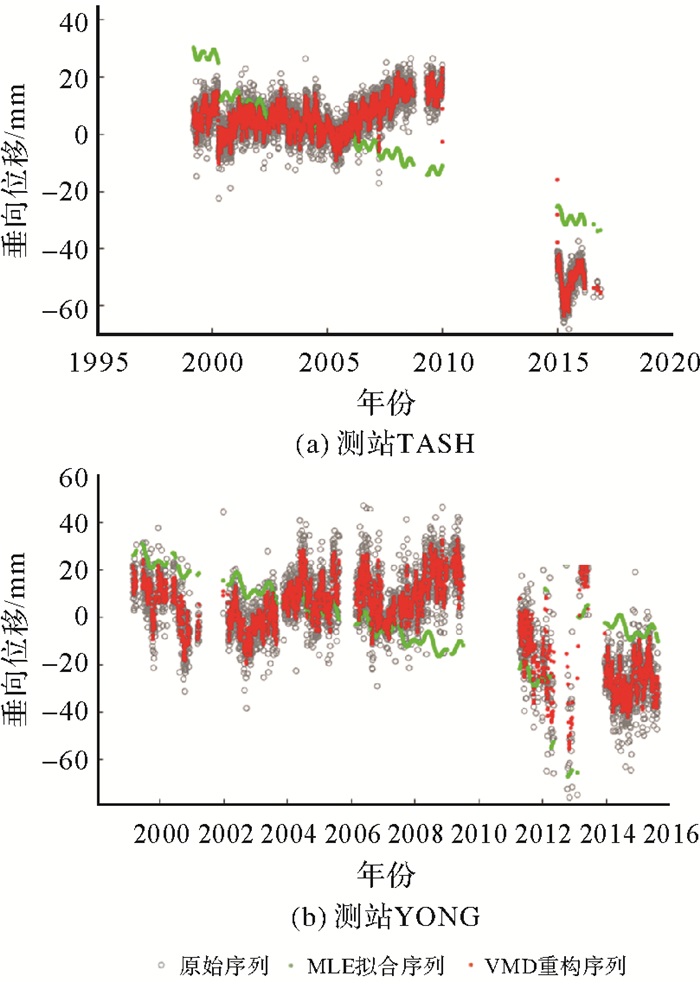
如图 9所示,测站TASH位于新疆塔什库尔干塔吉克自治县,该测站存在较长时间的数据缺失和较大的阶跃,当遗漏该阶跃信号时,MLE方法会错误估计原始序列,而VMD方法仍然能够较准确地得到反映测站实际变化的重构序列,因而使得RMSE改进率达到79.8%。同样地,位于南海永兴岛的测站YONG,存在较长时间的数据缺失和阶跃现象,MLE方法不能较好反映原始序列中的高频信号,使得RMSE改进率在所有CMONOC测站中最大,达到了104.6%。
|
| 图 9 存在阶跃信号的2个CMONOC测站 Fig. 9 Two CMONOC stations with offset signal |
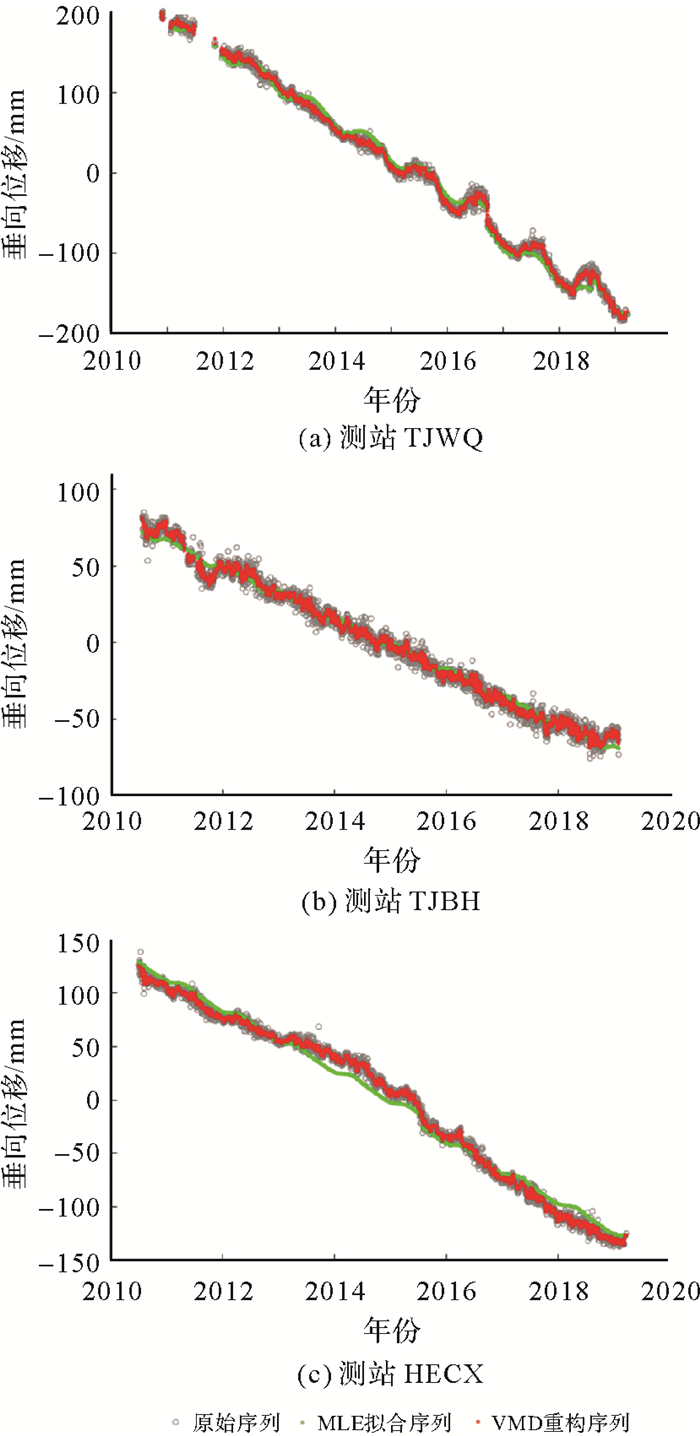
全部CMONOC测站中,有10个测站的RMSE改进率低于20%,其中最低的3个测站为TJWQ(7.8%)、TJBH(11.6%)和HECX(11.7%),它们的原始信号、拟合信号与重构信号分别如图 10所示。分析发现,这些测站均存在显著的趋势项。
|
| 图 10 RMSE改进率小于20%的3个CMONOC测站 Fig. 10 Three CMONOC stations with RMSE improvement rates smaller than 20% |
测站TJWQ(天津武清)由于近十年来华北平原地区地下水开采严重,导致地下水位逐年下降,目前该地区已成为世界上最大的地下水漏斗区[41-43],该测站位于漏斗中心区域。可以发现,该测站地下水下降造成了地表位置的逐年下降,2011—2014年,测站位置呈线性下降,而2014—2019年,测站位置在每年约6、7月出现明显的回升。对于这种整体呈线性趋势的原始序列,MLE方法与VMD方法均能够较好提取出测站中的线性项,相对而言,VMD能够更多地顾及测站的年度时变信号,因此RMSE改进率为7.8%。测站TJBH(天津滨海)、HECX(河北沧县)与测站TJWQ情况是一致的,其中HECX的信噪比在全部CMONOC测站中最大。
3 结语针对现有参数化方法不能有效拟合GNSS高程时间序列,以及一些非参数化方法(WD、EMD)在信号分解中存在的自适应性较差、模态混叠等缺点,本文将VMD方法应用于中国CMONOC测站高程时间序列的分析中,得出以下结论。
(1) 相对于MLE方法,VMD方法全部测站的RMSE改进率为正值,全部测站RMSE改进率的均值为69.8%,该方法有助于GNSS测站提取时变信号,减弱高程时间序列中的非线性形变,验证了VMD方法在CMONOC测站高程时间序列时变信号提取中的有效性。
(2) 当重构分量个数取3时,VMD方法得到的重构序列与原始序列之间的相关系数在全部CMONOC测站的均值近似为1,比MLE方法的相应结果提高了0.38;VMD方法得到的重构序列的信噪比在全部测站的均值为28.04 dB,比MLE方法的相应结果提高了24.9 dB。
(3) 虽然VMD方法具有较好的自适应性,但是IMF分量个数仍然与具体的每一个测站有关,当分解个数和重构分量选取恰当时,VMD方法在GNSS高程时间序列中的应用效果可进一步提高。
| [1] |
WANG Wei, QIAO Xuejun, WANG Dijin, et al. Spatiotemporal noise in GPS position time-series from Crustal Movement Observation Network of China[J]. Geophysical Journal International, 2019, 216(3): 1560-1577. DOI:10.1093/gji/ggy506 |
| [2] |
WU Shuguang, NIE Guigen, MENG Xiaolin, et al. Application of an annual phase-augmented clustering approach to annual detection of vertical GPS station deformation[J]. GPS Solutions, 2020, 25(1): 1-13. |
| [3] |
YAO Chaolong, LUO Zhicai, HU Yueming, et al. Detecting droughts in southwest China from GPS vertical position displacements[J]. Journal of Geodesy and Geoinformation Science, 2020, 3(2): 114. |
| [4] |
VAN DAM T, ALTAMIMI Z, COLLILIEUX X, et al. Topographically induced height errors in predicted atmospheric loading effects[J]. Journal of Geophysical Research: Solid Earth, 2010, 115(B7): B07415. |
| [5] |
JIANG Weiping, LI Zhao, VAN DAM T, et al. Comparative analysis of different environmental loading methods and their impacts on the GPS height time series[J]. Journal of Geodesy, 2013, 87(7): 687-703. DOI:10.1007/s00190-013-0642-3 |
| [6] |
CHANARD K, FLEITOUT L, CALAIS E, et al. Toward a global horizontal and vertical elastic load deformation model derived from GRACE and GNSS station position time series[J]. Journal of Geophysical Research: Solid Earth, 2018, 123(4): 3225-3237. DOI:10.1002/2017JB015245 |
| [7] |
YAN Haoming, CHEN Wu, ZHU Yaozhong, et al. Contributions of thermal expansion of monuments and nearby bedrock to observed GPS height changes[J]. Geophysical Research Letters, 2009, 36(13): L13301. |
| [8] |
XU Xueqing, DONG Danan, FANG Ming, et al. Contributions of thermoelastic deformation to seasonal variations in GPS station position[J]. GPS Solutions, 2017, 21(3): 1265-1274. DOI:10.1007/s10291-017-0609-6 |
| [9] |
KING M A, WILLIAMS S D P. Apparent stability of GPS monumentation from short-baseline time series[J]. Journal of Geophysical Research: Solid Earth, 2009, 114(B10): B10403. |
| [10] |
HILL E M, DAVIS J L, ELÓSEGUI P, et al. Characterization of site-specific GPS errors using a short-baseline network of braced monuments at Yucca Mountain, southern Nevada[J]. Journal of Geophysical Research: Solid Earth, 2009, 114(B11): B11402. |
| [11] |
NAHMANI S, BOCK O, BOUIN M N, et al. Hydrological deformation induced by the West African Monsoon: comparison of GPS, GRACE and loading models[J]. Journal of Geophysical Research: Solid Earth, 2012, 117(B5): B05409. |
| [12] |
YANG Kun, QIN Jun, ZHAO Long, et al. A multiscale soil moisture and freeze-thaw monitoring network on the third pole[J]. Bulletin of the American Meteorological Society, 2013, 94(12): 1907-1916. DOI:10.1175/BAMS-D-12-00203.1 |
| [13] |
姜卫平, 王锴华, 李昭, 等. GNSS坐标时间序列分析理论与方法及展望[J]. 武汉大学学报(信息科学版), 2018, 43(12): 2112-2123. JIANG Weiping, WANG Kaihua, LI Zhao, et al. Prospect and theory of GNSS coordinate time series analysis[J]. Geomatics and Information Science of Wuhan University, 2018, 43(12): 2112-2123. |
| [14] |
王敏, 沈正康. 中国大陆现今构造变形: 三十年的GPS观测与研究[J]. 中国地震, 2020, 36(4): 660-683. WANG Min, SHEN Zhengkang. Present-day tectonic deformation in continental China: thirty years of GPS observation and research[J]. Earthquake Research in China, 2020, 36(4): 660-683. |
| [15] |
姜卫平, 李昭, 刘鸿飞, 等. 中国区域IGS基准站坐标时间序列非线性变化的成因分析[J]. 地球物理学报, 2013, 56(7): 2228-2237. JIANG Weiping, LI Zhao, LIU Hongfei, et al. Cause analysis of the non-linear variation of the IGS reference station coordinate time series inside China[J]. Chinese Journal of Geophysics, 2013, 56(7): 2228-2237. |
| [16] |
BEVIS M, BROWN A. Trajectory models and reference frames for crustal motion geodesy[J]. Journal of Geodesy, 2014, 88(3): 283-311. DOI:10.1007/s00190-013-0685-5 |
| [17] |
张恒璟, 程鹏飞. 基于经验模式分解的CORS站高程时间序列分析[J]. 大地测量与地球动力学, 2012, 32(3): 129-134. ZHANG Hengjing, CHENG Pengfei. Analysis on time series of two cors stations ' height based on EMD[J]. Journal of Geodesy and Geodynamics, 2012, 32(3): 129-134. |
| [18] |
张恒璟, 程鹏飞. 基于EEMD的GPS高程时间序列噪声识别与提取[J]. 大地测量与地球动力学, 2014, 34(2): 79-83. ZHANG Hengjing, CHENG Pengfei. Noise recognition and extraction of GPS height time series based on EMD[J]. Journal of Geodesy and Geodynamics, 2014, 34(2): 79-83. |
| [19] |
贾瑞生, 赵同彬, 孙红梅, 等. 基于经验模态分解及独立成分分析的微震信号降噪方法[J]. 地球物理学报, 2015, 58(3): 1013-1023. JIA Ruisheng, ZHAO Tongbin, SUN Hongmei, et al. Micro-seismic signal denoising method based on empirical mode decomposition and independent component analysis[J]. Chinese Journal of Geophysics, 2015, 58(3): 1013-1023. |
| [20] |
戴前伟, 丁浩, 张华, 等. 基于变分模态分解和奇异谱分析的GPR信号去噪[J]. 吉林大学学报(地球科学版), 2022, 52(3): 701-712. DAI Qianwei, DING Hao, ZHANG Hua, et al. Noise reduction method of GPR signal based on VMD-SSA[J]. Journal of Jilin University (Earth Science Edition), 2022, 52(3): 701-712. |
| [21] |
HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[C]//Proceedings of 1998 Royal Society of London Series A: Mathematical, Physical and Engineering Sciences, London: the Royal Society Publishing, 1998, 454(1971): 903-995.
|
| [22] |
穆大鹏, 闫昊明. 全球平均海平面上升的瞬时速率[J]. 地球物理学报, 2018, 61(12): 4758-4766. MU Dapeng, YAN Haoming. The instantaneous rate of global mean sea level rise[J]. Chinese Journal of Geophysics, 2018, 61(12): 4758-4766. |
| [23] |
张双成, 李振宇, 何月帆, 等. GNSS高程时间序列周期项的经验模态分解提取[J]. 测绘科学, 2018, 43(8): 80-84, 96. ZHANG Shuangcheng, LI Zhenyu, HE Yuefan, et al. Extracting of periodic component of GNSS vertical time series using EMD[J]. Science of Surveying and Mapping, 2018, 43(8): 80-84, 96. |
| [24] |
刘希康, 丁志峰, 李媛, 等. EMD在GNSS时间序列周期项处理中的应用[J]. 武汉大学学报(信息科学版), 2023, 48(1): 135-145. LIU Xikang, DING Zhifeng, LI Yuan, et al. Application of EMD to GNSS time series periodic term processing[J]. Geomatics and Information Science of Wuhan University, 2023, 48(1): 135-145. |
| [25] |
鲁铁定, 钱文龙, 贺小星, 等. 一种削弱信噪混叠的EMD降噪方法[J]. 大地测量与地球动力学, 2020, 40(2): 111-116. LU Tieding, QIAN Wenlong, HE Xiaoxing, et al. An EMD noise reduction method for reducing signal noise aliasing[J]. Journal of Geodesy and Geodynamics, 2020, 40(2): 111-116. |
| [26] |
DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544. DOI:10.1109/TSP.2013.2288675 |
| [27] |
刘长良, 武英杰, 甄成刚. 基于变分模态分解和模糊C均值聚类的滚动轴承故障诊断[J]. 中国电机工程学报, 2015, 35(13): 3358-3365. LIU Changliang, WU Yingjie, ZHEN Chenggang. Rolling bearing fault diagnosis based on variational mode decomposition and fuzzy C means clustering[J]. Proceedings of the CSEE, 2015, 35(13): 3358-3365. |
| [28] |
吕中亮. 基于变分模态分解与优化多核支持向量机的旋转机械早期故障诊断方法研究[D]. 重庆: 重庆大学, 2016. LV Zhongliang. Research on incipient fault diagnosis methods for rotating machinery based on VMD and optimized MSVM[D]. Chongqing: Chongqing University, 2016. |
| [29] |
丁承君, 冯玉伯, 王曼娜. 基于变分模态分解与深度卷积神经网络的滚动轴承故障诊断[J]. 振动与冲击, 2021, 40(2): 287-296. DING Chengjun, FENG Yubo, WANG Manna. Rolling bearing fault diagnosis using variational mode decomposition and deep convolutional neural network[J]. Journal of Vibration and Shock, 2021, 40(2): 287-296. |
| [30] |
王煜尘, 窦银科, 孟润泉. 基于模糊C均值聚类-变分模态分解和群智能优化的多核神经网络短期负荷预测模型[J]. 高电压技术, 2022, 48(4): 1308-1319. WANG Yuchen, DOU Yinke, MENG Runquan. Forecasting model for multicore neural network short-term load based on fuzzy C-mean clustering-variational modal decomposition and chaotic swarm intelligence optimization[J]. High Voltage Engineering, 2022, 48(4): 1308-1319. |
| [31] |
叶剑华, 曹旌, 杨理, 等. 基于变分模态分解和多模型融合的用户级综合能源系统超短期负荷预测[J]. 电网技术, 2022, 46(7): 2610-2622. YE Jianhua, CAO Jing, YANG Li, et al. Ultra short-term load forecasting of user level integrated energy system based on variational mode decomposition and multi-model fusion[J]. Power System Technology, 2022, 46(7): 2610-2622. |
| [32] |
陆振宇, 卢亚敏, 夏志巍, 等. 基于变分模态分解和小波分析的语音信号去噪方法[J]. 现代电子技术, 2018, 41(13): 47-51. LU Zhenyu, LU Yamin, XIA Zhiwei, et al. Speech signal denoising method based on VMD and wavelet analysis[J]. Modern Electronics Technique, 2018, 41(13): 47-51. |
| [33] |
李宏, 李定文, 朱海琦, 等. 一种优化的VMD算法及其在语音信号去噪中的应用[J]. 吉林大学学报(理学版), 2021, 59(5): 1219-1227. LI Hong, LI Dingwen, ZHU Haiqi, et al. An optimized VMD algorithm and its application in speech signal denoising[J]. Journal of Jilin University (Science Edition), 2021, 59(5): 1219-1227. |
| [34] |
陈祥, 杨志强, 田镇, 等. GA-VMD与多尺度排列熵结合的GNSS坐标时序降噪方法[J]. 武汉大学学报(信息科学版), 2023, 48(9): 1425-1434. CHEN Xiang, YANG Zhiqiang, TIAN Zhen, et al. Denoising method for GNSS time series based on GA-VMD and multi-scale permutation entropy[J]. Geomatics and Information Science of Wuhan University, 2023, 48(9): 1425-1434. |
| [35] |
MAJUMDER I, DASH P K, BISOI R. Variational mode decomposition based low rank robust kernel extreme learning machine for solar irradiation forecasting[J]. Energy Conversion and Management, 2018, 171: 787-806. DOI:10.1016/j.enconman.2018.06.021 |
| [36] |
朱建军, 章浙涛, 匡翠林, 等. 一种可靠的小波去噪质量评价指标[J]. 武汉大学学报(信息科学版), 2015, 40(5): 688-694. ZHU Jianjun, ZHANG Zhetao, KUANG Cuilin, et al. A reliable evaluation indicator of wavelet denoising[J]. Geomatics and Information Science of Wuhan University, 2015, 40(5): 688-694. |
| [37] |
杨兵, 杨志强, 田镇, 等. 联合EMD-HD和小波分解的GNSS坐标时间序列降噪分析[J]. 测绘学报, 2022, 51(9): 1881-1889. YANG Bing, YANG Zhiqiang, TIAN Zhen, et al. Denoising analysis of GNSS coordinate time series by combining EMD-HD and wavelet decomposition[J]. Acta Geodaetica et Cartographica Sinica, 2022, 51(9): 1881-1889. DOI:10.11947/j.AGCS.2022.20210175 |
| [38] |
HERRING R, KING W, MCCLUSKY S. GAMIT/GLOBK reference manuals, release 10.4[R]. Cambridge: MIT Technical Reports, 2010.
|
| [39] |
REBISCHUNG P, GRIFFITHS J, RAY J, et al. IGS08: the IGS realization of ITRF2008[J]. GPS Solutions, 2012, 16(4): 483-494. DOI:10.1007/s10291-011-0248-2 |
| [40] |
GAZEAUX J, WILLIAMS S, KING M, et al. Detecting offsets in GPS time series: first results from the detection of offsets in GPS experiment[J]. Journal of Geophysical Research: Solid Earth, 2013, 118(5): 2397-2407. DOI:10.1002/jgrb.50152 |
| [41] |
FENG W, ZHONG M, LEMOINE J, et al. Evaluation of groundwater depletion in North China using the Gravity Recovery and Climate Experiment (GRACE) data and ground‐based measurements[J]. Water Resources Research, 2013, 49: 2110-2118. DOI:10.1002/wrcr.20192 |
| [42] |
HUANG Zhiyong, PAN Yun, GONG Huili, et al. Subregional-scale groundwater depletion detected by GRACE for both shallow and deep aquifers in North China Plain[J]. Geophysical Research Letters, 2015, 42(6): 1791-1799. DOI:10.1002/2014GL062498 |
| [43] |
GONG Huili, PAN Yun, ZHENG Longqun, et al. Long-term groundwater storage changes and land subsidence development in the North China Plain (1971—2015)[J]. Hydrogeology Journal, 2018, 26(5): 1417-1427. DOI:10.1007/s10040-018-1768-4 |



