2. 地理信息工程国家重点实验室, 陕西 西安 710054;
3. 国家卫星海洋应用中心, 北京 100081;
4. 中国科学院精密测量科学与技术创新研究院, 湖北 武汉 430077
2. State Key Laboratory of Geo-Information Engineering, Xi'an 710054, China;
3. National Satellite Ocean Application Service, Beijing 100081, China;
4. Innovation Academy for Precision Measurement Science and Technology, Chinese Academy of Sciences, Wuhan 430077, China
海洋重力是海洋环境信息的重要组成部分,精确的构建海洋重力模型在地球重力场建模[1]、海底地形反演[2]、地质构造探测[3]及水下匹配导航[4]等方面具有重要的意义。目前,获取海洋重力数据的手段主要有基于海洋重力仪的观测(包括船载、机载及固定海底的重力仪观测等)、重力卫星观测和卫星测高反演技术等[5-6]。基于海洋重力仪的观测主要获取航迹线上的高精度重力数据,在获取全球或大范围的海洋重力数据时效率较低,并且受地缘政治因素的限制,重力卫星观测和卫星测高技术不受观测条件的限制能够高效地获取全球海洋重力数据[7-8]。由于重力卫星观测主要获取中长波重力信号,而卫星测高反演技术能够获取中短波重力信号,因此卫星测高技术对于反演全球海洋重力场具有独特的优势[9-11]。
自20世纪70年代测高任务执行以来,测高数据在海洋重力异常反演方面就展现了巨大的应用潜力[12-14]。随着卫星测高技术和测高任务的发展,测高数据质量和数据量都得到了极大提升[15-16],相应的海洋重力异常模型反演精度相比早期的模型也得到了极大改善[17-18]。然而,目前卫星测高反演海洋重力异常主要是利用沿轨的相邻观测数据,而跨轨观测数据由于兼顾轨迹覆盖密度存在长时间间隔引起的海面时变误差,导致跨轨方向的观测数据并不能充分利用[19-20]。考虑到卫星运行轨道通常设计为南北向(已有测高任务的轨道倾角通常要≥66°),由沿轨数据解算的垂线偏差南北分量和东西分量精度并不均衡,极大地限制了海洋重力异常反演精度的进一步改善[21-22]。此外,大多数测高数据主要由雷达信号测量,在靠近陆地、岛屿的复杂海域,雷达信号极易受到非同质反射面的干扰[23-24],导致海面高观测的数据质量和数据量明显降低,从而也影响了复杂海域海洋重力异常模型的反演精度[25-26]。
ICESat-2[27]是由美国国家航空航天局(NASA)于2018年9月15日成功发射的第二代激光测高卫星,轨道倾角为92°,通过搭载先进地形激光测高系统(advanced topographic laser altimeter, ATLAS),能够同时获取3对激光束(每对激光束包括强波束-弱波束)观测数据,且相邻波束对的地面轨间距仅为3.3 km。因此,在利用沿轨数据的同时,还能基于多个波束解算跨轨方向的数据,提高东西方向上数据的有效利用,从而改善海洋重力异常反演精度。此外,ICESat-2海面高的光斑直径相比于雷达测高脉冲足迹由千米量级减小至17 m,ICESat-2测高数据能够有效弥补雷达测高数据在复杂海域的缺失[28]。ICESat-2获取的海面高数据在局部的海面地形、垂线偏差解算和海面高异常变化观测等方面的应用已得到了有效评价[29-31],而对于已发布的全球海洋重力异常模型还罕有利用ICESat-2测高数据。基于此,本文呈现了ICESat-2集成沿轨和跨轨数据的海洋重力场反演方法,并对ICESat-2反演的全球海洋重力异常模型的精度进行了分析评估,旨在为未来的宽刈幅测高数据和国产双星跟飞模式的测高数据处理提供理论指导。
1 数据与处理 1.1 ICESat-2数据本文主要采用ICESat-2 Level-3A的ATL12海面高程产品[32],该产品中的海面高主要是由Level 2A的全球定位光子数据产品ATL03导出的。由于ATL03提供了来自海面、海底和大气等全部返回的光子数据,该产品也被广泛用于近海水深反演。而本文使用的海面高信息首先根据置信度参数对ATL03中的原始光子数据进行粗去噪,基于光子点密度分布可分离出具有代表性的海面光子数据;然后通过累积8000个海面光子数据或者沿轨7 km范围内的海面光子数据来获得平均的海面高。因此,本文使用的海面高信息是有效顾及了ICESat-2光子计数激光的海水穿透性。
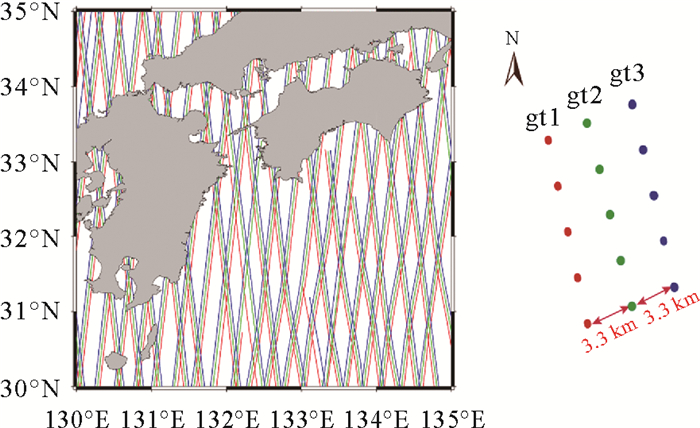
ATL12产品中提供了3对波束(每对为强波束-弱波束)的海面高观测数据,海面高已进行了必要的地球物理校正、大气延迟改正和海况偏差校正等, 该产品可通过NASA的Earthdata获取(https://search.earthdata.nasa.gov/)。在海洋区域,ATL12的弱波束数据只有少量的数据量,因此本次试验主要基于3个强波束(gt1、gt2、gt3)的观测数据反演海洋重力异常模型。本文中使用的观测数据时间范围为2018年10月至2022年10月(cycle001-cycle017),一个周期(cycle011)的地面轨迹如图 1所示,3个波束在沿轨方向的相邻观测点平均地面距离分别为2.6、2.8和2.6 km。
|
| 图 1 ICESat-2 3个强波束的地面轨迹 Fig. 1 ICESat-2 ground track of three strong beams |
1.2 船载重力数据
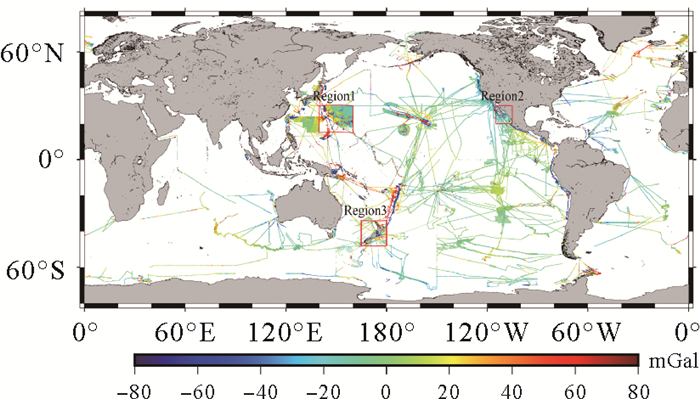
为了评估测高反演海洋重力异常模型的精度,本文通过美国国家环境信息中心(NCEI)获取了全球船载重力异常数据。考虑到导航精度对于船载重力观测精度的影响,只获取了20世纪90年代以后的观测数据。由于NCEI提供的船载重力数据是收集的不同机构不同时间观测的重力数据,本文对船载重力数据进行了再处理。首先,对每条航线采用3倍中误差剔除了与参考重力场EGM2008存在异常的船载重力数据;然后,采用二次多项式对每条航线的船载重力数据进行了校正[33-34]。全球船载重力数据剔除率约为2.9%,总计剩余点7 012 812个(486航次),如图 2所示。
|
| 图 2 全球船载重力异常数据(NCEI, 1990年之后) Fig. 2 Global Shipborne gravity anomalies from NCEI after 1990s |
此外,本文还通过自然资源部第二海洋研究所(简称“海洋二所”)获取了中国南海局部海域的船载重力异常数据。总计有12航次的13 288个点。全球船载重力和南海局部区域的船载重力异常与地球重力参考场EGM2008差异的统计结果见表 1。
| 船载重力 | 最大值 | 最小值 | 平均值 | 标准差 | 均方根误差 |
| 全球海域 | 99.62 | -96.35 | -0.15 | 6.27 | 6.27 |
| 南海局部海域 | 16.63 | -14.02 | 0.02 | 2.96 | 2.96 |
1.3 全球重力场模型
为了分析ICESat-2测高数据反演的海洋重力异常模型,本文获取了国际常用的全球海洋重力异常模型,包括美国斯克里普斯海洋研究所(SIO)发布的Sandwell and Smith(S & S)系列[35]和丹麦科技大学DTU系列模型[17],截至2023年4月发布的最新版本分别为V32.1和DTU17。同时还获取了由山东科技大学发布的全球海洋重力异常模型SDUST2021GRA[18]。这些模型都是基于多源测高数据构建的1′×1′格网数据,都还未使用ICESat-2测高数据,各个模型信息见表 2。
| 全球海洋重力异常模型 | 参考重力场 | 纬度覆盖范围 | 主要测高数据 |
| DTU17 | EGM2008 | 90°S—90°N | Topex/Poseidon, Jason-1/2/3, ERS-1/2, Envisat, Cryosat-2 (LRM/SAR), SARAL/AltiKa |
| SIO V32.1 | EGM2008 | 80°S—80°N | Topex/Poseidon, Jason-1/2/3, ERS-2, Envisat, Cryosat-2 (LRM/SAR), SARAL/AltiKa, Sentinel-3A/3B |
| SDUST2021 GRA | XGM2019e | 80°S—80°N | Topex/Poseidon, Jason-1/2/3, Envisat, Cryosat-2 (LRM), SARAL/AltiKa, HY-2A |
此外,根据国际全球海洋重力异常建模常采用的参考重力场,在本文试验中也采用地球重力场模型EGM2008(球谐系数展开至2160阶和2159次)[36]作为参考重力场。本文通过国际全球地球模型中心(ICGEM, http://icgem.gfz-potsdam.de)获取了该模型参考阶次为2160的1′×1′格网重力异常数据。
2 多波束激光数据反演重力异常方法 2.1 常规沿轨数据反演方法基于卫星测高数据的海洋重力异常反演,通常由海面高数据解算沿轨大地水准面高梯度作为重要的输入参数。为了从沿轨海面高数据中解算大地水准面高,从沿轨海面高数据中减去相应观测点上由全球稳态海面地形模型MDT-CNES-CLS18[37]获取的结果。在海洋重力异常反演过程中,为了有效利用海面高数据解算短波长的重力信号,通常采用移去恢复技术,从沿轨海面高数据解算大地水准面高的基础上,移除参考大地水准面高模型获取剩余大地水准面高,利用沿轨剩余大地水准面高梯度反演短波长重力异常信号,进而再恢复参考地球重力场的中长波信号,获得卫星测高反演的海洋重力异常模型。基于沿轨海面高数据解算剩余大地水准面高梯度的公式为
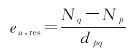 (1)
(1)
式中,eα, res为p和q位置中心点的剩余大地水准面高梯度;α为方位角;Np和Nq分别是p点和q点的剩余大地水准面高,主要是通过沿轨海面高减去稳态海面地形和参考大地水准面高模型获取的结果;dpq是两点的球面距离。
基于剩余的大地水准面高梯度,采用最小二乘配置法(LSC)解算格网垂线偏差,LSC公式为
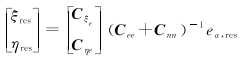 (2)
(2)
式中,ξres和ηres分别是剩余垂线偏差的子午分量和卯酉分量;Cξe(或Cηe)是剩余子午分量(或卯酉分量)和大地水准面高梯度的互协方差矩阵;Cee是大地水准面高梯度的方差矩阵;Cnn是大地水准面高梯度的噪声方差矩阵。
在采用最小二乘配置法时,需要确定各波束数据的海面高梯度观测误差。依据误差传播定律,当忽略两点间的距离误差时,海面高梯度的观测误差可表示为
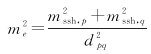 (3)
(3)
式中,me为海面高梯度中误差,用于确定Cnn;mssh, p和mssh, q分别为p点和q点的海面高中误差。
基于格网垂线偏差,进而利用逆Vening-Meinesz公式反演海洋重力异常
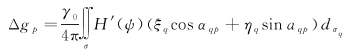 (4)
(4)
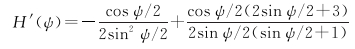 (5)
(5)
式中,γ0是正常重力;H′(ψ)是采用的核函数[38];dσq是单位球面积分单元。
在使用逆Vening-Meinesz公式计算重力异常时,积分区域包含计算点会导致核函数奇异,称为内圈带效应。常采用的内圈带区域重力异常计算公式为
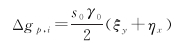 (6)
(6)
式中,ξy和ηx是通过沿轨大地水准面高梯度数值微分得到的垂线偏差子午分量和卯酉分量;s0为内圈带大小
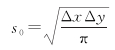 (7)
(7)
式中,Δx和Δy是格网垂线偏差的间隔。
2.2 集成沿轨和跨轨数据反演方法ICESat-2不仅能够获得沿轨方向的海面高梯度,还能依据3个强波束的观测数据解算跨轨方向的海面高梯度。集成沿轨和跨轨数据反演方法与沿轨数据反演方法的主要差别是跨轨海面高梯度的确定,以及沿轨海面高梯度和跨轨海面高梯度的融合,因此本节主要描述这两方面的内容。
由于ICESat-2 3个波束的观测并不是完全同步的,需要确定不同波束上用于解算跨轨方向的海面高观测值;如果不确定相应的海面高观测值,则基于两个波束上的海面高观测值可以解算多个方向的海面高梯度,但大多数的海面高梯度的方位角偏离跨轨方向。基于ICESat-2 3个波束数据解算跨轨海面高梯度的处理策略为:①从3个沿波束数据中选择观测数据量最少的一条波束数据作为参考数据;②基于参考波束数据的观测时间,在时间阈值的约束下确定另一条波束上是否存在某一时间阈值范围内的观测数据,以确保解算跨轨海面高梯度的方位角更偏向于东西方向;③如果两个波束上存在时间阈值范围内的海面高观测数据,则利用两个波束上时间间隔最短的海面高解算跨轨海面高梯度,如果不存在,则该参考点被剔除不能用于跨轨海面高梯度的计算。处理策略的公式可表示为
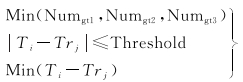 (8)
(8)
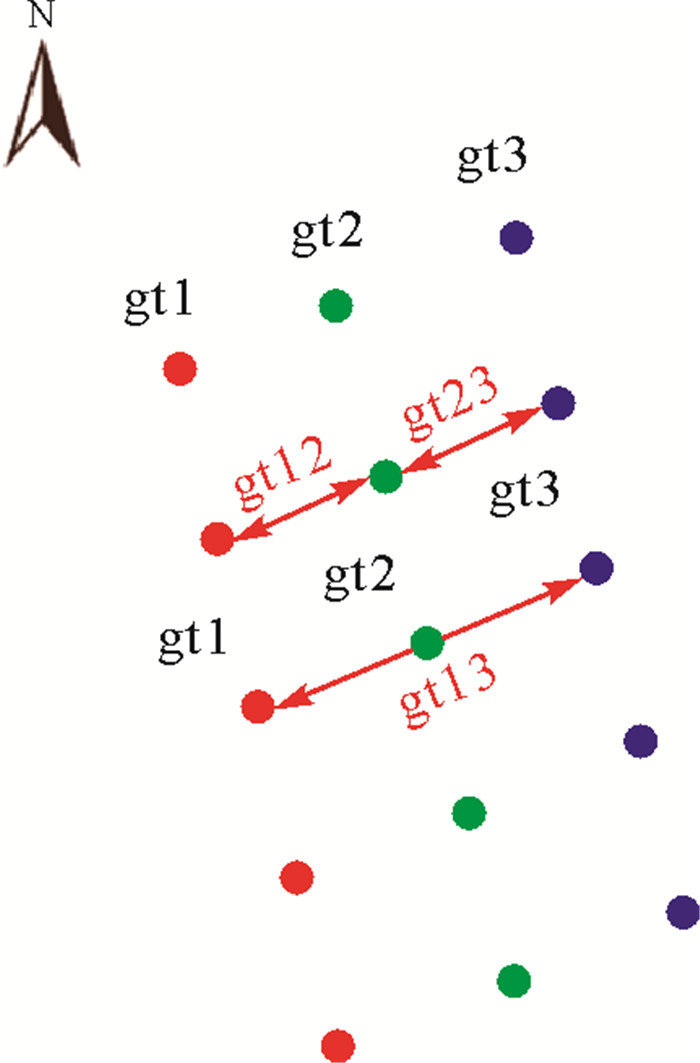
式中,Numgt1、Numgt2、Numgt3分别为3个波束的数据量;Trj为参考轨迹的第j个观测点的观测时间;Ti为另一条轨迹的第i个观测点的观测时间;Threshold为时间阈值,本文试验中为1 s。由任意两个波束数据解算的跨轨海面高梯度命名为gt12、gt23、gt13,确定沿轨和跨轨海面高梯度的示意如图 3所示。
|
| 图 3 沿轨和跨轨数据解算海面高梯度 Fig. 3 Determining sea surface height gradients from along-track data and cross-track data |
在获得跨轨海面高梯度后,需要融合沿轨海面高梯度。LSC是一种常用的数据融合方法,沿轨和跨轨海面高梯度融合的关键在于确定噪声方差矩阵Cnn。对于沿轨海面高梯度的观测误差主要是基于每个波束相邻的海面高观测误差确定的,而对于跨轨海面高梯度的观测误差可通过相应波束上的海面高观测误差确定。
基于沿轨数据和跨轨数据解算的格网垂线偏差,然后利用逆Vening-Meinesz公式反演海洋重力异常。
3 结果与分析 3.1 沿轨数据反演模型结果为了确定ICESat-2测高数据质量,本文统计了从2018年10月至2022年10月3个强波束观测数据的海面高交叉不符值,以及与全球平均海平面模型MSS_CNES_CLS2015的差异。在计算海面高交叉点不符值时,考虑到两个轨迹的观测时间间隔:如果时间间隔较短,则交叉点数量较少;如果时间间隔较长,则海面高时变会对交叉点不符值造成影响。本文基于30 d间隔范围内观测数据确定交叉点不符值,在局部区域(120°E—140°E, 20°N—40°N)的统计结果见表 3。由表 3可知,ICESat-2 3个波束的海面高数据质量是可靠的。此外,本文还统计了1′×1′范围内海面高的平均数量,约为1.01个,因而从测高数据质量和测高数据量方面表明ICESat-2能够用于反演格网为1′×1′的海洋重力异常模型。
| 统计值 | ICESat-2波束 | 最大值 | 最小值 | 平均值 | 标准差 | 均方根误差 |
| 海面高交叉点不符值(交叉点个数) | gt1(1669) | 0.385 | -0.391 | 0.002 | 0.117 | 0.117 |
| gt2(1451) | 0.411 | -0.411 | 0.002 | 0.109 | 0.109 | |
| gt3(1640) | 0.431 | -0.421 | 0.004 | 0.119 | 0.119 | |
| 与MSS_CNES_CLS2015模型的差异 | gt1 | 0.444 | -0.468 | 0.005 | 0.122 | 0.122 |
| gt2 | 0.430 | -0.479 | 0.008 | 0.128 | 0.128 | |
| gt3 | 0.459 | -0.486 | 0.002 | 0.128 | 0.128 |
在采用最小二乘配置法时,需要确定采用数据的窗口长度。不同球面距离窗口长度范围内测高数据反演的局部海洋重力异常(120°E—140°E, 20°N—40°N)与船载重力差异的均方根误差(RMS)见表 4。考虑到反演海洋重力场反演的精度及窗口长度范围越大耗时越多,本文试验中采用窗口长度为0.6°范围内的测高数据解算格网垂线偏差。进而本文基于3个波束的沿轨海面高数据反演了1′×1′的全球海洋重力异常模型(80°S—80°N),命名为IS2Gra_alo模型。由于沿轨数据反演的模型与集成沿轨和跨轨数据反演的模型图像很难区分,本文只绘制了集成沿轨和跨轨数据反演的全球海洋重力异常模型。
| 窗口长度范围/(°) | RMS/mGal |
| 0.2 | 5.63 |
| 0.4 | 5.57 |
| 0.6 | 5.55 |
| 0.8 | 5.54 |
| 1.0 | 5.54 |
为了评估模型的精度,本文统计了IS2Gra_alo模型与全球船载重力的差异,模型数据内插到船载重力位置重力差异的统计结果见表 5。在全球范围内,IS2Gra_alo模型与船载重力异常差异的RMS为5.70 mGal,在中低纬度海域RMS较低,而在高纬度海域其RMS较高,这可能与测高数据质量有关。进而本文统计了在中低纬度局部区域(120°E—140°E,20°N—40°N)和高纬度局部区域(180°E—160°W,80°S—60°S)的海面高交叉点不符值,其RMS分别为0.116、0.127 m。此外,IS2Gra_alo模型与全球海洋重力异常模型差异的RMS约为3 mGal(表 6)。通过对比NCEI全球船载重力数据和已发布的全球海洋重力异常模型,验证了基于ICESat-2 3个强波束数据反演海洋重力异常模型的可靠性,表明ICESat-2能够为高精度、高分辨率的海洋重力异常反演提供新轨迹的观测数据。
| 区域 | 全球海洋重力异常模型 | 最大值 | 最小值 | 平均值 | 标准差 | 均方根误差 |
| 全球海域(80°S—80°N) | DTU17 | 99.25 | -71.85 | -0.13 | 5.42 | 5.42 |
| SDUST2021GRA | 99.12 | -68.45 | -0.11 | 5.19 | 5.19 | |
| SIO V32.1 | 77.17 | -86.24 | -0.10 | 5.18 | 5.18 | |
| IS2Gra_alo | 97.98 | -67.65 | -0.10 | 5.70 | 5.70 | |
| IS2Gra_alo_acr | 96.38 | -67.31 | -0.08 | 5.54 | 5.54 | |
| 高纬度海域(80°S—60°S, 60°N—80°N) | DTU17 | 99.46 | -71.85 | -0.25 | 9.82 | 9.82 |
| SDUST2021GRA | 99.12 | -68.45 | -0.26 | 9.72 | 9.73 | |
| SIO V32.1 | 77.17 | -76.54 | -0.21 | 9.53 | 9.54 | |
| IS2Gra_alo | 97.98 | -66.85 | -0.10 | 9.95 | 9.95 | |
| IS2Gra_alo_acr | 96.38 | -65.70 | -0.13 | 9.89 | 9.89 | |
| 中低纬度海域(60°S—60°N) | DTU17 | 78.44 | -71.85 | -0.12 | 4.89 | 4.89 |
| SDUST2021GRA | 64.14 | -65.57 | -0.10 | 4.63 | 4.63 | |
| SIO V32.1 | 76.25 | -86.23 | -0.06 | 4.65 | 4.65 | |
| IS2Gra_alo | 65.25 | -67.65 | -0.09 | 5.21 | 5.21 | |
| IS2Gra_alo_acr | 66.24 | -67.31 | -0.08 | 5.03 | 5.03 |
| ICESat-2海洋重力异常模型 | DTU17 | SDUST2021GRA | SIO V32.1 | |||||
| 平均值 | 均方根误差 | 平均值 | 均方根误差 | 平均值 | 均方根误差 | |||
| IS2Gra_alo | 0.00 | 2.50 | 0.00 | 2.63 | 0.08 | 3.35 | ||
| IS2Gra_alo_acr | 0.00 | 2.30 | 0.00 | 2.46 | 0.08 | 3.25 | ||
3.2 集成沿轨和跨轨数据反演模型结果
基于3个沿轨和gt13跨轨数据解算的海面高梯度也反演了1′×1′的全球海洋重力异常模型,命名为IS2Gra_alo_acr模型(https://doi.org/10.5281/zenodo.8378225),如图 4所示。对于跨轨数据组合的选择,主要呈现在第4部分的讨论中。在本节主要评估IS2Gra_alo_acr模型精度和相对于沿轨数据模型IS2Gra_alo的差异。

|
| 图 4 集成ICESat-2沿轨和跨轨数据反演的全球海洋重力异常模型(IS2Gra_alo_acr) Fig. 4 ICESat-2 global marine gravity anomaly model (IS2Gra_alo_acr) recovered from along-track and cross-track altimeter data |
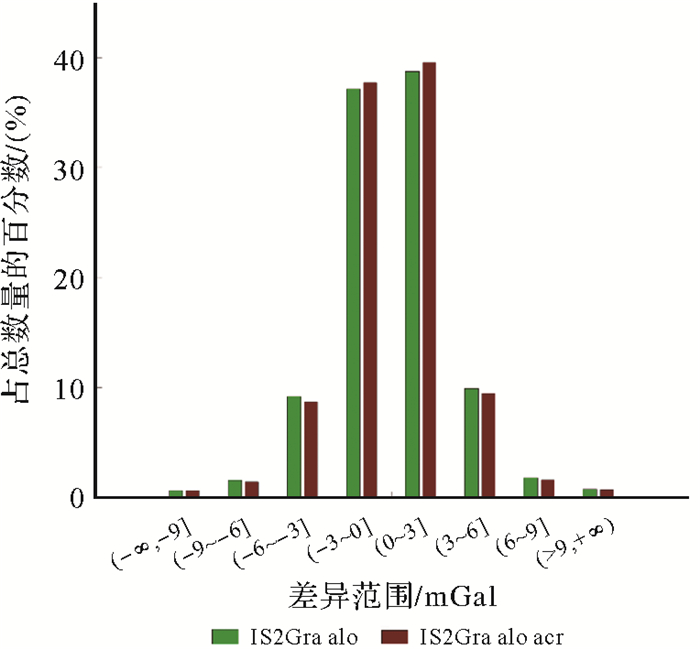
IS2Gra_alo_acr模型与全球船载重力差异的统计结果见表 5,其RMS为5.54 mGal,相比由IS2Gra_alo模型获取的RMS减少了0.16 mGal。在高纬度和中低纬度海域,IS2Gra_alo_acr模型的RMS都要优于IS2Gra_alo模型的结果。此外,本文也统计了IS2Gra_alo_acr与全球海洋重力异常模型的差异,其统计结果见表 6。IS2Gra_alo_acr与全球海洋重力异常模型差异的RMS相比IS2Gra_alo模型的结果至少减少了0.10 mGal。IS2Gra_alo_acr、IS2Gra_alo模型与SIO V32.1模型差异的分布直方图如图 5所示,IS2Gra_alo_acr与SIO V32.1的差异主要集中在-3~3 mGal,其数据量占总数据量的78%,优于IS2Gra_alo模型的结果(75%)。以上研究结果表明通过补充跨轨海面高梯度数据能够有效提高海洋重力异常反演的精度。
|
| 图 5 ICESat-2全球海洋重力异常模型与SIO V32.1差异的分布直方图 Fig. 5 Histograms of difference between ICESat-2 gravity anomaly models and SIO V32.1 |
考虑到全球可公开获取的船载重力数据质量稍差,本文又对比了中国南海局部海域少量高质量的船载重力数据,见表 7。全球海洋重力异常模型与船载重力异常差异的RMS约为2.30 mGal,而基于ICESat-2测高数据反演海洋重力异常模型的RMS约为2.72 mGal,明显优于对比NCEI全球船载重力异常的结果,进一步验证了ICESat-2测高数据反演海洋重力异常模型的可靠性。此外,由IS2Gra_alo_acr模型获取的RMS相对于IS2Gra_alo模型改善了0.10 mGal,这与全球海洋重力异常的评估基本是一致的。
| 海洋重力异常模型 | 最大值 | 最小值 | 平均值 | 标准差 | 均方根误差 |
| SIO V32.1 | 15.83 | -12.43 | -0.09 | 2.28 | 2.28 |
| SDUST2021 | 17.64 | -12.69 | -0.07 | 2.32 | 2.32 |
| DTU17 | 18.17 | -13.36 | 0.04 | 2.37 | 2.37 |
| IS2Gra_alo | 18.23 | -12.65 | -0.10 | 2.82 | 2.82 |
| IS2Gra_alo_acr | 18.08 | -12.52 | -0.10 | 2.72 | 2.72 |
为了进一步分析IS2Gra_alo与IS2Gra_alo_acr模型在不同海域的差异,本文又选择了3个局部海域进行对比分析,如图 1所示。由表 8可知,不同局部区域IS2Gra_alo_acr模型相对于IS2Gra_alo模型分别改善了0.12、0.18、0.08 mGal,在不同地区有着不同程度的改善,这可能主要与局部海洋表面状况、局部海洋重力特征有关,因此ICESat-2测高数据对于局部区域海洋重力场精度的改善仍有待进一步的研究。
| 局部区域 | ICESat-2海洋重力异常模型 | 最大值 | 最小值 | 平均值 | 标准差 | 均方根误差 |
| Region1 | IS2Gra_alo | 46.00 | -28.98 | 0.07 | 3.94 | 3.94 |
| IS2Gra_alo_acr | 45.92 | -29.88 | 0.06 | 3.82 | 3.82 | |
| Region2 | IS2Gra_alo | 49.85 | -46.95 | -0.18 | 5.83 | 5.83 |
| IS2Gra_alo_acr | 49.17 | -45.35 | -0.15 | 5.65 | 5.65 | |
| Region3 | IS2Gra_alo | 48.83 | -49.68 | -0.32 | 6.90 | 6.91 |
| IS2Gra_alo_acr | 47.68 | -49.92 | -0.33 | 6.82 | 6.83 |
4 讨论
ICESat-2能够同时获得3个强波束的观测数据,任意两个波束数据组合都能解算跨轨海面高梯度,为了选择较优的跨轨数据组合,本文给出了4种组合方案:gt12、gt23、gt12/gt23、gt13,并联合3个沿轨数据反演海洋重力异常。不同跨轨数据联合沿轨数据反演的局部海域海洋重力异常(120°E—140°E,20°N—40°N)与船载重力差异的统计结果见表 9。
| 海洋重力异常模型 | 最大值 | 最小值 | 平均值 | 标准差 | 均方根误差 |
| gt1+gt2+gt3 | 50.81 | -48.59 | -0.10 | 5.55 | 5.55 |
| gt12+gt1+gt2+gt3 | 50.35 | -48.08 | -0.10 | 5.60 | 5.60 |
| gt23+gt1+gt2+gt3 | 54.92 | -54.98 | -0.06 | 5.91 | 5.91 |
| gt12+gt23+gt1+gt2+gt3 | 49.77 | -49.87 | -0.08 | 5.83 | 5.83 |
| gt13+gt1+gt2+gt3 | 50.02 | -47.68 | -0.06 | 5.44 | 5.44 |
在沿轨数据的基础上,通过补充gt13跨轨海面高梯度有效提高了海洋重力异常反演的精度,而补充gt12或者gt23跨轨海面高梯度并没有明显改善沿轨数据反演海洋重力异常的精度。对此本文进行了原因分析,gt1、gt2、gt3 3个强波束海面高交叉点不符值的RMS分别为0.117、0.109及0.119 m,中间波束gt2测高数据的精度略高,但总体上3个波束的观测数据质量基本一致。
本文又统计了沿轨和跨轨海面高梯度的差异,见表 10。gt13跨轨海面高梯度与参考场大地水准面高梯度差异的标准差(standard deviation, STD)基本与沿轨海面高梯度的结果一致,而gt12或gt23跨轨海面高梯度的STD与沿轨海面高梯度的结果有明显偏差,这表明在沿轨海面高梯度的基础上,补充数据质量较差的跨轨海面高梯度可能会降低海洋重力异常模型反演的精度。在认为3个强波束观测数据质量一致的情况下,gt13与gt12或者gt23解算海面高梯度的差异主要体现在采用不同距离下的海面高数据。gt12或gt23的地面轨间距只有3.3 km,而gt13的地面轨间距为6.6 km,较小的轨间距可能影响了解算的跨轨海面高梯度质量。
| 参数 | gt1 | gt2 | gt3 | gt12 | gt23 | gt13 |
| 数据量 | 538, 699 | 416, 801 | 502, 096 | 397, 456 | 351, 986 | 400, 853 |
| 标准差/(″) | 2.43 | 2.91 | 2.45 | 3.16 | 3.29 | 2.54 |
为了利用相邻波束上较长距离的观测数据解算海面高梯度,本文又探讨了与沿轨方向夹角为45°和135°方向数据联合沿轨数据反演海洋重力异常模型的精度。首先,基于时间阈值(2 s)的约束确定跨轨观测数据上相应的海面高;然后,基于时间阈值范围内的跨轨观测数据确定与沿轨方向夹角约为45°和135°的海面高梯度联合3个沿轨海面高梯度反演海洋重力异常,确定45°/135°方向海面高梯度与沿轨海面高梯度的示意如图 6所示。由表 11可知,集成gt1245/135(或者gt2345/135)数据相比集成gt12数据(或者gt23数据)反演的海洋重力异常精度略有提升,但总体上仍要略低于集成gt13跨轨数据和沿轨数据反演海洋重力异常的结果。因此,本文主要集成gt13跨轨海面高梯度和沿轨海面高梯度反演全球海洋重力异常模型。

|
| 图 6 确定45°/135°方向海面高梯度与沿轨海面高梯度的示意 Fig. 6 The schematic diagram of determining sea surface height gradients from along-track data and cross-track data with a direction of 45°/135° |
| ICESat-2重力异常模型 | 最大值 | 最小值 | 平均值 | 标准差 | 均方根 |
| gt1245/135+gt1+gt2+gt3 | 50.79 | -47.15 | -0.03 | 5.31 | 5.58 |
| gt2345/135+gt1+gt2+gt3 | 48.62 | -48.73 | -0.09 | 5.32 | 5.88 |
| gt1245/135+gt2345/135+ gt1+gt2+gt3 | 49.24 | -48.22 | -0.04 | 5.18 | 5.80 |
| gt1345/135+gt1+gt2+gt3 | 50.87 | -49.75 | -0.05 | 5.45 | 5.45 |
5 结论
测高任务的发展为卫星测高反演海洋重力场提供了新颖的观测数据。新型激光测高ICESat-2能够同时获得3对激光光束的观测数据,在利用沿轨数据的同时还能利用跨轨数据反演海洋重力异常,为进一步优化海洋重力异常模型提供了可能。本文首先给出了集成沿轨和跨轨海面高梯度反演海洋重力异常的处理策略,进而又分别利用沿轨数据和集成数据反演了全球海洋重力异常模型(IS2Gra_alo和IS2Gra_alo_acr)。通过对比全球船载重力数据和全球海洋重力异常模型,验证了ICESat-2激光测高数据反演海洋重力异常的可靠性,ICESat-2激光测高数据能够和雷达测高数据一样用于高精度高分辨率的海洋重力异常模型反演。
集成沿轨数据和跨轨数据反演的全球海洋重力异常模型IS2Gra_alo_acr与全球船载重力差异的RMS为5.54 mGal,相比沿轨数据模型IS2Gra_alo的精度提高了0.16 mGal,IS2Gra_alo_acr与已发布的全球海洋重力异常模型(DTU17、SDUST2021GRA、SIO V32.1)差异的RMS分别为2.30、2.46和3.25 mGal,相比IS2Gra_alo的精度至少提高了0.10 mGal,研究结果表明通过补充跨轨数据能够有效提高沿轨数据反演海洋重力异常的精度。本文通过探讨不同波束观测数据组合解算跨轨海面高梯度对海洋重力异常反演精度的影响,确定了集成两侧跨波束(gt13)数据相比集成相邻波束数据对沿轨数据反演结果的改善效果更明显。此外,本文还探讨了采用不同方向的跨轨海面高梯度数据对海洋重力异常反演精度的影响,对于相邻波束观测数据采用45°/135°方向的跨轨海面高梯度能够有效提高反演海洋重力异常模型的精度,但总体上集成两侧跨轨数据与沿轨数据反演的海洋重力异常模型较优。
本文通过探讨不同跨轨数据组合,以及解算不同方向的海面高梯度数据对海洋重力异常反演精度的影响,为未来SWOT宽刈幅测高数据和我国自主双星跟飞测高数据反演海洋重力异常模型提供了理论指导。此外,本文反演的全球海洋重力异常模型主要是基于ICESat-2单一测高数据,为了获得高精度高分辨率的全球海洋重力异常模型(1~2 mGal)仍需要联合多源测高数据。
致谢: 感谢Earthdata提供的ICESat-2激光测高数据;感谢美国国家环境信息中心(NCEI)提供的全球船载重力异常数据。
| [1] |
ZINGERLE P, PAIL R, GRUBER T, et al. The combined global gravity field model XGM2019e[J]. Journal of Geodesy, 2020, 94(7): 66. DOI:10.1007/s00190-020-01398-0 |
| [2] |
XU Chuang, LI Jinbo, JIAN Guangyu, et al. An adaptive nonlinear iterative method for predicting seafloor topography from altimetry-derived gravity data[J]. Journal of Geophysical Research: Solid Earth, 2023, 128(1): e2022JB025692. DOI:10.1029/2022JB025692 |
| [3] |
HWANG C, CHANG E T Y. Seafloor secretsr evealed[J]. Science, 2014, 346: 32-33. DOI:10.1126/science.1260459 |
| [4] |
李晓平, 周贤高, 宫京. 重力匹配导航要素影响机理建模与试验验证[J]. 中国惯性技术学报, 2021, 29(6): 777-781, 787. LI Xiaoping, ZHOU Xiangao, GONG Jing. Factor influencing mechanism modeling and test validation of gravity map matching navigation[J]. Journal of Chinese Inertial Technology, 2021, 29(6): 777-781, 787. |
| [5] |
李杨, 郭金运, 孙玉, 等. 联合时变重力数据与测高数据反演全球海平面变化及其分量贡献[J]. 测绘学报, 2022, 51(8): 1768-1778. LI Yang, GUO Jinyun, SUN Yu, et al. Inversion of global sea level change and its component contributions by combining time-varying gravity data and altimetry data[J]. Acta Geodaetica et Cartographica Sinica, 2022, 51(8): 1768-1778. DOI:10.11947/j.AGCS.2022.20210169 |
| [6] |
GREEN C M, FLETCHER K M U, CHEYNEY S, et al. Satellite gravity-enhancements from new satellites and new altimeter technology[J]. Geophysical Prospecting, 2019, 67(6): 1611-1619. DOI:10.1111/1365-2478.12697 |
| [7] |
SANDWELL D T, MULLER R D, SMITH W H F, et al. New global marine gravity model from CryoSat-2 and Jason-1 reveals buried tectonic structure[J]. Science, 2014, 346(6205): 65-67. DOI:10.1126/science.1258213 |
| [8] |
SCHWABE J, SCHEINERT M. Regional geoid of the Weddell Sea, Antarctica, from heterogeneous ground-based gravity data[J]. Journal of Geodesy, 2014, 88(9): 821-838. DOI:10.1007/s00190-014-0724-x |
| [9] |
ZHANG Shengjun, ABULAITIJIANG A, ANDERSEN O B, et al. Comparison and evaluation of high-resolution marine gravity recovery via sea surface heights or sea surface slopes[J]. Journal of Geodesy, 2021, 95(6): 66. DOI:10.1007/s00190-021-01506-8 |
| [10] |
JIN Taoyong, ZHOU Mao, ZHANG Huan, et al. Analysis of vertical deflections determined from one cycle of simulated SWOT wide-swath altimeter data[J]. Journal of Geodesy, 2022, 96(4): 30. DOI:10.1007/s00190-022-01619-8 |
| [11] |
孙中苗, 管斌, 翟振和, 等. 海洋卫星测高及其反演全球海洋重力场和海底地形模型研究进展[J]. 测绘学报, 2022, 51(6): 923-934. SUN Zhongmiao, GUAN Bin, ZHAI Zhenhe, et al. Research progress of ocean satellite altimetry and its recovery of global marine gravity field and seafloor topography model[J]. Acta Geodaetica et Cartographica Sinica, 2022, 51(6): 923-934. DOI:10.11947/j.AGCS.2022.20220069 |
| [12] |
ANDERSEN O B, KNUDSEN P. Global marine gravity field from the ERS-1 and Geosat geodetic mission altimetry[J]. Journal of Geophysical Research: Oceans, 1998, 103(C4): 8129-8137. DOI:10.1029/97JC02198 |
| [13] |
郭金运, 朱风顺, 刘新, 等. 基于卫星测高的孟加拉湾海洋时变重力研究[J]. 华中科技大学学报(自然科学版), 2023, 51(3): 85-91, 99. GUO Jinyun, ZHU Fengshun, LIU Xin, et al. Time-varying marine gravity of Bay of Bengal derived from CryoSat-2 altimetry data[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2023, 51(3): 85-91, 99. |
| [14] |
FAN Diao, LI Shanshan, MENG Shuyu, et al. Bathymetric prediction from multi-source satellite altimetry gravity data[J]. Journal of Geodesy and Geoinformation Science, 2019, 2(1): 49-58. |
| [15] |
GUAN Bin, SUN Zhongmiao, LIU Xiaogang, et al. Feasibility analysis of performance validation for satellite altimeters using tide gauge and deep-ocean bottom pressure recorder[J]. Journal of Geodesy and Geoinformation Science, 2020, 3(1): 102-109. |
| [16] |
LI Zhen, GUO Jinyun, JI Bing, et al. A review of marine gravity field recovery from satellite altimetry[J]. Remote Sensing, 2022, 14(19): 4790. DOI:10.3390/rs14194790 |
| [17] |
ANDERSEN O B, KNUDSEN P. The DTU17 global marine gravity field: first validation results[C]//Proceedings of 2019 International Association of Geodesy Symposia. Cham: Springer International Publishing, 2019: 83-87.
|
| [18] |
ZHU Chengcheng, GUO Jinyun, YUAN Jiajia, et al. SDUST2021GRA: global marine gravity anomaly model recovered from Ka-band and Ku-band satellite altimeter data[J]. Earth System Science Data, 2022, 14(10): 4589-4606. DOI:10.5194/essd-14-4589-2022 |
| [19] |
ABDALLA S, KOLAHCHI A A, ABLAIN M, et al. Altimetry for the future: building on 25 years of progress[J]. Advances in Space Research, 2021, 68(2): 319-363. DOI:10.1016/j.asr.2021.01.022 |
| [20] |
WAN Xiaoyun, HAO Ruijie, JIA Yongjun, et al. Global marine gravity anomalies from multi-satellite altimeter data[J]. Earth, Planets and Space, 2022, 74(1): 165. DOI:10.1186/s40623-022-01720-4 |
| [21] |
孙和平, 孙文科, 申文斌, 等. 地球重力场及其地学应用研究进展: 2020中国地球科学联合学术年会专题综述[J]. 地球科学进展, 2021, 36(5): 445-460. SUN Heping, SUN Wenke, SHEN Wenbin, et al. Research progress of earth's gravity field and its application in geosciences: a summary of annual meeting of Chinese Geoscience Union in 2020[J]. Advances in Earth Science, 2021, 36(5): 445-460. |
| [22] |
YU Daocheng, HWANG C, ANDERSEN O B, et al. Gravity recovery from SWOT altimetry using geoid height and geoid gradient[J]. Remote Sensing of Environment, 2021, 265: 112650. DOI:10.1016/j.rse.2021.112650 |
| [23] |
GUO Jinyun, LUO Hongxin, ZHU Chengcheng, et al. Accuracy comparison of marine gravity derived from HY-2A/GM and CryoSat-2 altimetry data: a case study in the Gulf of Mexico[J]. Geophysical Journal International, 2022, 230(2): 1267-1279. DOI:10.1093/gji/ggac114 |
| [24] |
WU Yihao, WANG Junjie, ABULAITIJIANG A, et al. Local enhancement of marine gravity field over the spratly islands by combining satellite SAR altimeter-derived gravity data[J]. Remote Sensing, 2022, 14(3): 474. DOI:10.3390/rs14030474 |
| [25] |
PASSARO M, ROSE S K, ANDERSEN O B, et al. ALES+: adapting a homogenous ocean retracker for satellite altimetry to sea ice leads, coastal and inland waters[J]. Remote Sensing of Environment, 2018, 211: 456-471. DOI:10.1016/j.rse.2018.02.074 |
| [26] |
ABULAITIJIANG A, ANDERSEN O B, BARZAGHI R, et al. Coastal marine gravity modelling from satellite altimetry-case study in the Mediterranean[J]. Journal of Geodetic Science, 2021, 11(1): 29-37. DOI:10.1515/jogs-2020-0200 |
| [27] |
MARKUS T, NEUMANN T, MARTINO A, et al. The ice, cloud, and land Elevation Satellite-2 (ICESat-2): science requirements, concept, and implementation[J]. Remote Sensing of Environment, 2017, 190: 260-273. DOI:10.1016/j.rse.2016.12.029 |
| [28] |
BUZZANGA B, HEIJKOOP E, HAMLINGTON B D, et al. An assessment of regional ICESat-2 sea-level trends[J]. Geophysical Research Letters, 2021, 48(9): e92327. |
| [29] |
YU Yao, SANDWELL D T, GILLE S T, et al. Assessment of ICESat-2 for the recovery of ocean topography[J]. Geophysical Journal International, 2021, 226(1): 456-467. DOI:10.1093/gji/ggab084 |
| [30] |
CHE Defu, LI Hang, ZHANG Shengjun, et al. Calculation of deflection of vertical and gravity anomalies over the South China Sea derived from ICESat-2 data[J]. Frontiers in Earth Science, 2021, 9: 379. |
| [31] |
LIU Xin, HUI Guihua, GUO Jinyun, et al. Inversion of deflection of the vertical in the South China Sea using ICESat-2 sea surface height data[J]. Remote Sensing, 2022, 15(1): 30. DOI:10.3390/rs15010030 |
| [32] |
MORISON J H, HANCOCK D, DICKINSON J, et al. ATLAS/ICESat-2 L3A ocean surface height, Version 5. [EB/OL]. [2022-11-12]. https://doi.org/10.5067/ATLAS/ATL12.005.
|
| [33] |
ZHU Chengcheng, GUO Jinyun, GAO Jinyao, et al. Marine gravity determined from multi-satellite GM/ERM altimeter data over the South China Sea: SCSGA V1.0[J]. Journal of Geodesy, 2020, 94(5): 50. DOI:10.1007/s00190-020-01378-4 |
| [34] |
郭金运, 张鸿飞, 李真, 等. 基于多源船载重力异常数据的联合再处理——以墨西哥湾为例[J/OL]. 武汉大学学报(信息科学版), 1-23. [2022-11-12]. https://doi.org/10.13203/j.whugis20230088. GUO Jinyun, ZHANG H, LI Z, et al. Joint reprocessing of shipborne gravity anomalies based on multi-sources: a case study of Gulf of Mexico[J/OL]. Geomatics and Information Science of Wuhan University, 1-23. [2022-11-12]. https://doi.org/10.13203/j.whugis20230088. |
| [35] |
SANDWELL D T, HARPER H, TOZER B, et al. Gravity field recovery from geodetic altimeter missions[J]. Advances in Space Research, 2021, 68(2): 1059-1072. DOI:10.1016/j.asr.2019.09.011 |
| [36] |
PAVLIS N K, HOLMES S A, KENYON S C, et al. The development and evaluation of the Earth Gravitational Model 2008 (EGM 2008)[J]. Journal of Geophysical Research: Solid Earth, 2012, 117(B4): B04406. |
| [37] |
MULET S, RIO M H, ETIENNE H, et al. The new CNES-CLS18 global mean dynamic topography[J]. Ocean Science, 2021, 17(3): 789-808. DOI:10.5194/os-17-789-2021 |
| [38] |
HWANG C, HSU H Y, JANG R J. Global mean sea surface and marine gravity anomaly from multi-satellite altimetry: applications of deflection-geoid and inverse Vening Meinesz formulae[J]. Journal of Geodesy, 2002, 76(8): 407-418. DOI:10.1007/s00190-002-0265-6 |



