2. 武汉引力与固体潮国家野外科学观测研究站, 湖北 武汉 430071;
3. 武汉大学测绘学院, 湖北 武汉 430079;
4. 湖南省测绘科技研究所, 湖南 长沙 410007
2. Wuhan Gravitation and Solid Earth Tides National Observation and Research Station, Wuhan 430071, China;
3. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
4. Hunan Institute of Surveying, Mapping Sciences and Technology, Changsha 410007, China
海洋重力异常是地球重力场模型构建、海底地形反演、海洋资源勘探、冰川学等地球学科及应用研究的重要数据。海洋重力仪可以直接获取海洋重力异常,但测量成本较高,测量周期较长且重复性差,无法在短时间内获取大空间范围的海洋重力场信息,因此单纯依靠传统海洋实测数据恢复全球海域高精度高分辨率重力场是十分困难的。卫星测高技术可以实现对全球范围内海面高的全天候、连续准确探测,其效率和覆盖范围是传统海洋重力测量无法比拟的,已经成为获取海洋重力异常信息的主要数据源。
1985年大地测量卫星GeoSat(Geodetic Satellite)发射,海洋重力场反演得到了快速发展[1]。ERS-1/2、T/P(Topex/Poseidon)、Jason-1/2/3、GFO(GeoSat Follow-on)、EnviSat(environmental Satellite)、ICEsat(ice、cloud and land elevation satellite)及CryoSat-2(cryosphere satellite)等任务实施后,多个高精度、高分辨率的全球海洋重力异常模型相继发布[2-9],其中比较有代表性的模型有两组,分别是丹麦技术大学(Technical University of Denmark,DTU)Andersen课题组研发的DTU系列模型和美国加利福尼亚大学圣迭戈分校斯克里普斯海洋研究所(Scripps institution of Oceanography,SIO)Sandwell课题组研发的S&S(Sandwell & Smith)系列模型。2010年以后,DTU和SIO分别持续更新发布了多个空间分辨率1′×1′的全球海洋重力场模型,其中,DTU模型有DTU10、DTU13、DTU15和DTU17等,SIO模型有V19.1、V20.1、V22.1、V23.1等,最新版本为V32.1。
目前,全球海洋重力异常模型精度评价主要集中在采用船载重力实测数据进行外部检核或者模型互检两个方面[10-12]。本文利用球面小波对DTU10、DTU17和V32.1等模型进行多尺度分析,探究各尺度下模型间的差异,并从模型构建所采用的方法、数据和模型等多个角度深入探讨了引起差异的原因;在球面小波多尺度分解结果上,基于小波多尺度信号对应的空间分辨率和异常体场源深度信息,对传统径向基函数方法进行了改进,实现了不同深度情况下基于径向基函数的多尺度分析。
1 模型及方法介绍 1.1 模型介绍本文使用的模型有DTU10、DTU17和SIO V32.1,各模型基本情况见表 1。
| 模型名称 | 发布年份 | 所用数据及时间范围 | 覆盖范围 |
| DTU10 | 2010 | Geosat、ERS-1、T/P、ERS-2、GFO、Jason-1、Envisat、ICESat | 90°S—90°N |
| DTU17 | 2017 | T/P、ERS-2、GFO、Jason-1、Envisat、ICESat、Cryosat-2、SARAL/Altika | 90°S—90°N |
| S&S V32.1 | 2022 | Geosat、ERS-1、T/P、ERS-2、GFO、Jason-1、Envisat、Jason-2、Cryosat-2、SARAL/Altika、Sentinel-3A/B | 80°S—80°N |
DTU10是在DNSC08(采用了ERS-1、GEOSAT、ICESAT、T/P、JASON-1、ERS-2、GFO ERM及Envisat等卫星测高数据)的基础上,对所有ERS-2和Envisat数据进行重跟踪得到的,所利用的海潮模型为GOT4.7(Goddard Ocean tide),分辨率为0.5°×0.5°。
DTU17模型构建时采用海潮模型FES2014,分辨率为0.125°×0.125°。与DTU10相比,DTU17模型增加了Cryosat-2、Jason-1/GM和SARAL/Altika观测数据,主要提高了海岸、北极地区重力场精度,以及重力场短波(10~15 km)的精度[13]。其中,DTU17模型使用了更多的GM测高数据,但相对后续GM任务卫星,Geosat/GM、ERS-1精度不高,故DTU17模型构建时未采用Geosat/GM和ERS-1的数据。
SIO V32.1模型解算采用了SARAL、CryoSat-2、Jason-1/2、Sentinel-3A/B、Envisat和其他卫星测高数据,与DTU17模型不同的是使用了更长时间段的Cryosat-2、Jason-1/GM和SARAL/Altika等卫星观测数据,增加了Jason-2、Sentinel-3A/B观测值;对Jason-1/2、Envisat、Altika、Cryosat LRM(low resolution mode)进行了波形重跟踪,将有效波高significant wave height, SWH平滑滤波器的长波由45 km降低至30 km,降低了波长大于30 km信号的噪声水平,减小了陆海边缘效应。
除了模型构建所用数据源不同外,构建方法也不同,DTU采用海洋大地水准面高通过逆Stokes公式来计算重力异常,而SIO则采用了逆Vening-Meinesz公式利用垂线偏差求解重力异常[2, 14]。
1.2 球面小波多尺度分析方法DOG球面小波在空间域和频率域都有较好的局部化特性,在GPS速度场、重力场多尺度分析中具有较好效果[15-16],故本文选择DOG球面小波函数来进行多尺度分析
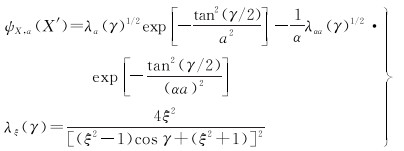 (1)
(1)
式中, X为球面小波的中心极,X∈S2(球面);a=2-q,其中,q为尺度,取整数;γ为极X(λ, φ)和球面点X′(λ′, φ′)之间的夹角;(λ, φ)和(λ′, φ′)为点的经纬度;α>1,用于调节函数形状;λξ为参数方程。
利用球面小波函数表达重力信号,需要建立球面小波框架,可以通过对小波函数中心极的位置和尺度进行离散化得到。基于正二十面体进行球面三角剖分,可得到不同尺度下的球面格网,进而得到一系列离散化的球面格点,以此来建立小波框架。将q=1, 2, 3,…,qmax时剖分得到的球面格点作为不同尺度下球面小波的中心极,得到与qmax对应的球面小波框架F
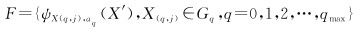 (2)
(2)
式中,ψ为DOG球面小波函数;X(q, j)为球面小波的中心极;aq=2-q,q为尺度;j为格网点序号;Gq为球面格网点。
设地球平均半径r=6371 km,不同尺度对应的空间分辨率见表 2[17]。
| 尺度 | 空间分辨率 | |
| q | aq | |
| 0 | 20 | 9 167.1 km |
| 1 | 2-1 | 5 260.7 km |
| 2 | 2-2 | 2 747.3 km |
| 3 | 2-3 | 1 389.9 km |
| 4 | 2-4 | 697.0 km |
| 5 | 2-5 | 348.8 km |
| 6 | 2-6 | 174.4 km |
| 7 | 2-7 | 87.2 km |
| 8 | 2-8 | 43.6 km |
| 9 | 2-9 | 21.8 km |
| 10 | 2-10 | 10.9 km |
1.3 球面径向基函数多尺度分析方法
设σR是半径为R的Bjerhammar球球面,ExtσR、IntσR分别代表球外、球内空间。在空间中有两点,z为测站位置向量,位于Bjerhammar球外;y为球面径向基函数中心点的位置向量,位于Bjerhammar球内,定义球面径向基函数为[18-19]
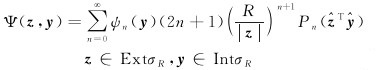 (3)
(3)
式中,ψn(y)为Legendre系数,决定了球面径向基函数的类型;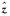
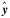
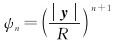 (4)
(4)
定义dt=R-|y|为球面径向基函数的深度,该参数与球面径向基函数的频谱带宽共同定义了球面径向基函数的空间带宽。空间带宽常定义为球面径向基函数最大值的一半,且假设空间带宽仅由一个参数p所决定,即球面径向基函数低于Bjerhammar球的深度。
基函数的深度和网络设计对建模的精度有很大的影响。由于Reuter格网具有全球均匀分布的特点,故常将球面径向基函数中心点置于Reuter格网的节点上,且文献[18]指出球面径向基函数之间的平均间隔应大于数据分辨率的两倍,通常以此作为Reuter格网分辨率的设置依据,并采用广义交叉验证(generalized cross-validation, GCV)技术通过迭代获得基函数深度与空间分辨率的最优组合。
传统球面径向基函数的深度和空间分辨率均是固定值、单一值,而本文对该方法进行了改进,尝试实现基于球面径向基函数的不同深度、不同空间分辨率的多尺度分析。
1.4 等效场源深度反演方法径向对数功率谱分析是地球物理领域反演等效场源深度的常用方法。在极坐标下,重力异常功率谱满足以下公式[20-21]
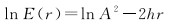 (5)
(5)
式中,ln E(r)为重力异常的径向对数功率谱;A为尺寸系数;h为场源埋深;r为波数。由式(5)可知,ln E(r)与波数r呈线性关系,斜率为-2h,故场源等效埋深为
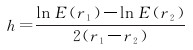 (6)
(6)
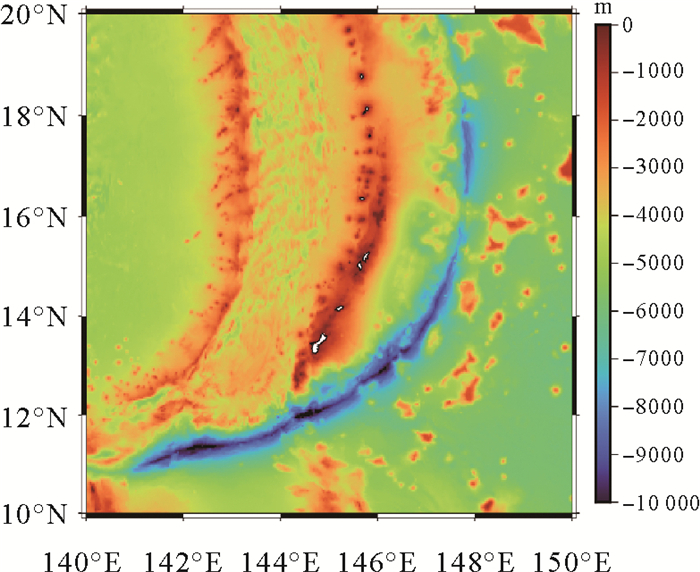
本文以马里亚纳海沟区域(140°E—150°E,10°N—20°N)作为试验区域,马里亚纳海沟是世界第一大海沟,被誉为地球的“第四极”,海底地形复杂,有沉没山脉、深海平原、湾谷及丘陵等,除关岛、罗塔岛、天宁岛、塞班岛等马里亚纳群岛外,其余均为海域,如图 1所示,图 1基于SRTM15+全球地形产品绘制,该地形产品利用船载测深数据和卫星测高深度反演数据获得[22],由Open Topography于2021年发布。
|
| 图 1 研究区域地形 Fig. 1 Topography of the research area |
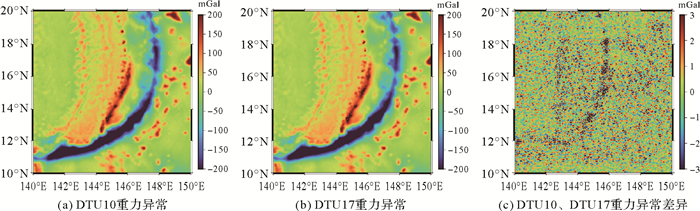
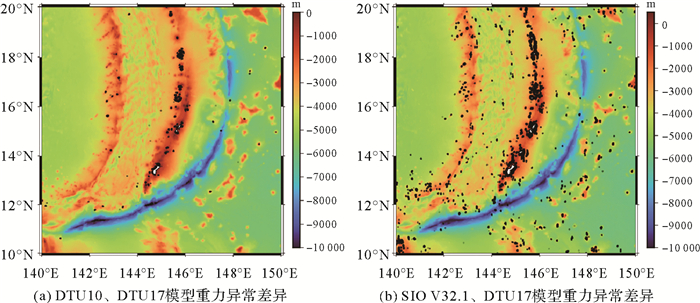
马里亚纳海沟区域重力异常变化明显(图 2),分布与地形呈现相关性,在复杂构造区域变化剧烈,在海底山脉区域重力异常为正值,在海沟区域,重力异常为负值。
|
| 图 2 DTU10、DTU17模型重力异常及差异 Fig. 2 Gravity anomaly and the difference between DTU10 and DTU17 |
需要特别说明的是,利用球面小波进行多尺度分析时通常选择一参考模型计算残差,并对残差进行多尺度分析,但计算残差的过程会将部分波段的信号移去,无法完全体现重力异常模型不同尺度下信号的特点,所以本文直接对DTU10、DTU17、SIO V32.1重力异常模型进行多尺度分析。
2.1 DTU模型分析结果DTU10、DTU17重力异常间差异不大,标准差约为1.30 mGal,较大的差异主要集中在海底山脉、海沟附近(图 2(c)),经统计,62%以上集中在±1 mGal以内,97%以上集中在±3 mGal以内。超过±5 mGal的仅占0.32%,其中,约20%的点位零星分布在海底山脉、海沟、海山地区,其他约80%的点位集中在关岛、罗塔岛、天宁岛、塞班岛、阿纳塔汉岛等马里亚纳群岛附近,具体分布情况如图 5(a)所示。
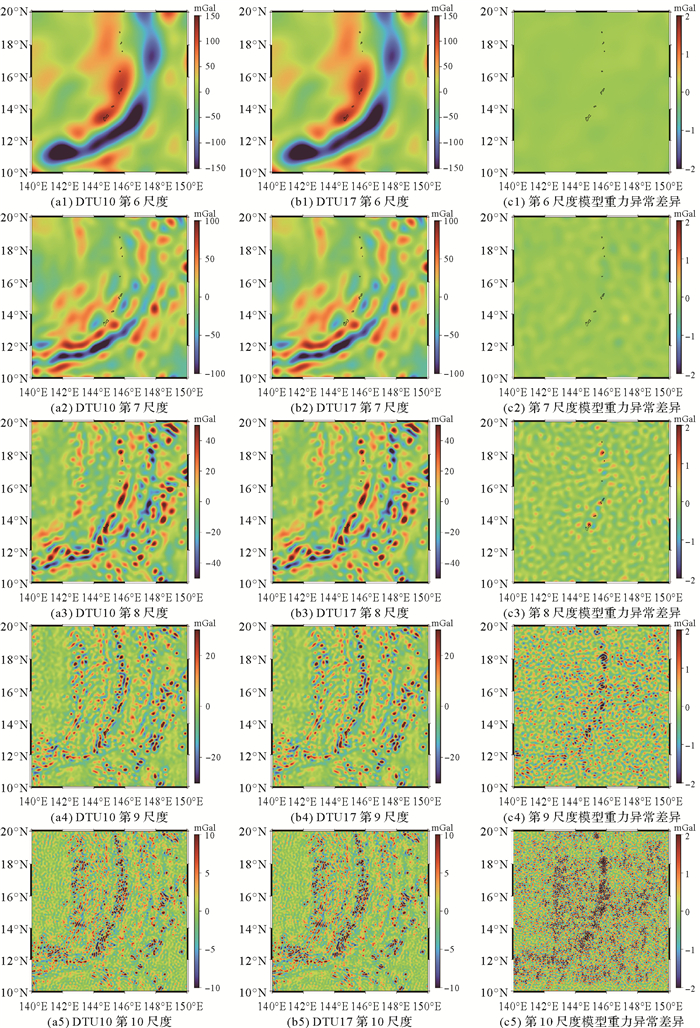
图 3(a)、(b)分别显示了DTU10、DTU17模型重力异常球面小波多尺度(q=6,7,8,9,10)分析结果,随着尺度的变小,重力异常分量的空间分辨率变高(由174.4 km增大到10.9 km,详见表 2),所反映的地球内部质量异常细节信息变多。第6、7两个尺度提取的是海沟、大的海山、丘陵等较大地质体的信号,是模型重力异常的主要信号源;第8尺度反映的是空间分辨率在43.6~87.2 km之间的地质体产生的重力异常信号,主要集中在马里亚纳群岛、马里亚纳海沟,以及马里亚纳海沟西南方向的海山附近;第9、10尺度反映了更多的细节信号,由空间分辨率高于43.6 km的更小场源物质产生,场源同样分布在马里亚纳群岛、马里亚纳海沟和海沟西南区域。
|
| 图 3 DTU10、DTU17模型重力异常球面小波多尺度分析结果 Fig. 3 Multi-scale analysis of DOG spherical wavelet for DTU10 and DTU17 gravity anomaly |
图 3(c)图反映了各尺度DTU10、DTU17重力异常分量的差异。随着尺度变小,差异增大,与DTU17模型增强重力场短波(10~15 km)的精度[13]一致,差异主要集中在小尺度第10和9,标准差分别为1.94、1.23 mGal,而第6、7、8尺度差异较小,最大标准差仅为0.23 mGal。因Cryosat-2、Jason-1/GM数据在赤道处的地面轨迹间距均达7 km,可以认为这两类数据的加入是产生第10尺度重力异常分量差异的主要原因;海潮模型分辨率由0.5°×0.5°提升至0.125°×0.125°,是引起第9尺度分量差异的主要因素;而SARAL/Altika观测数据在赤道处的地面轨迹间距约为80 km,对DTU17模型精度提升作用相对较小。
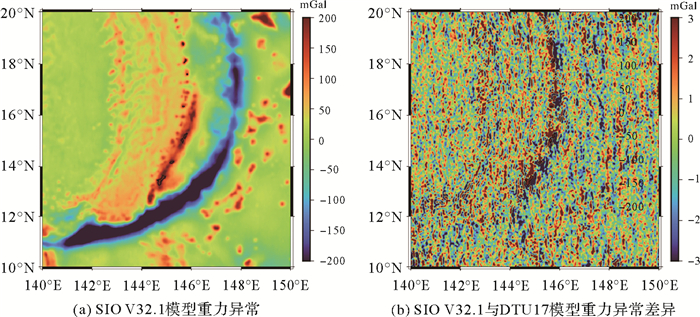
2.2 SIO模型分析结果SIO系列模型在2010年后发布的版本众多,但在本文中,只对最新的V32.1版本进行多尺度分析。该模型与DTU17模型差异的90%集中在±3 mGal以内(图 4),标准差约为2.15 mGal,大于DTU10和DTU17模型之间的差异。
|
| 图 4 SIO V32.1模型重力异常及与DTU17重力异常的差异 Fig. 4 Gravity anomaly of SIO V32.1 and the difference between SIO V32.1 and DTU17 |
SIO V32.1、DTU17重力异常差异值超过±5 mGal的约占3.01%,是DTU10和DTU17重力异常差异超过±5 mGal的10倍,具体分布情况如图 5(b)所示,与图 5(a)类似,大部分点位集中在马里亚纳群岛。
|
| 图 5 重力异常值差异超过±5 mGal的点位分布情况 Fig. 5 Distribution of these points, gravity anomaly difference of which more than ±5 mGal |
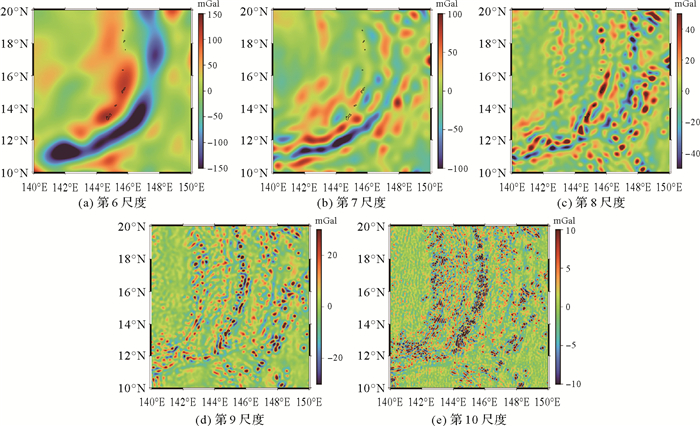
SIO V32.1重力异常模型DOG球面小波多尺度分析结果见图 6,与DTU模型分析结果类似,随着尺度变小,各分量信号对应的空间分辨率变高,细节信息更多,反映出更多体积更小或埋深更浅的地质体的信号。
|
| 图 6 SIO V32.1重力异常模型球面小波多尺度分析结果 Fig. 6 Multi-scale analysis of DOG spherical wavelet for SIO V32.1 gravity anomaly model |
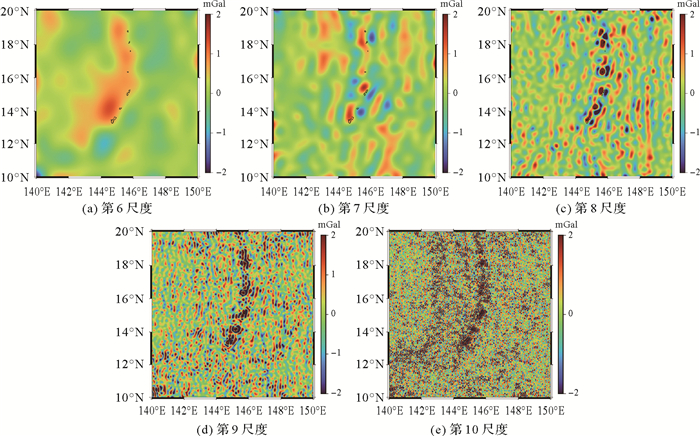
图 7(a)—(e)分别显示了SIO V32.1模型各尺度重力异常分量与DTU17模型各分量的差异。与DTU10、DTU17各尺度重力异常差异类似的是,随着尺度变小,差异增大(表 3);而不同点在于,第9、10尺度下SIO V32.1与DTU17重力异常分量的差异相对较小,第6~8尺度下SIO V32.1与DTU17重力异常分量差异相对较大(第6~8尺度下SIO V32.1与DTU17重力异常分量差异的标准差分别为0.34、0.41、0.62 mGal,而DTU10与DTU17重力异常分量差异的标准差分别为0.05、0.09、0.23 mGal)。这说明与DTU10、DTU17重力异常差异主要集中在第9、10尺度不同,SIO V32.1、DTU17模型的差异体现在各个尺度中,分析其原因有:①解算方法的差异,DTU10、DTU17模型解算方法一致,采用海洋大地水准面高通过逆Stokes公式计算重力异常,而SIO则采用逆Vening-Meinesz公式利用垂线偏差求解重力异常;②观测数据的贡献,与DTU17模型相比,SIO V32.1模型使用了更长时间段的Cryosat-2、Jason-1/GM和SARAL/Altika等卫星观测数据,增加了Jason-2、Sentinel-3A/B观测值,而这些数据提高了对空间分辨率为7、80、104和315 km信号的探测能力,进而影响了相应尺度的重力异常信号;③波形重跟踪的影响,SIO V32.1模型构建时对Jason-1/2、Envisat、Altika、Cryosat LRM进行了波形重跟踪,将有效波高(SWH)平滑滤波器的长波由45 km降低至30 km,降低了波长大于30 km的SWH的噪声水平,减小陆海边缘效应的同时,影响了第7、8尺度下两模型的差异。
|
| 图 7 SIO V32.1与DTU17各尺度重力异常分量的差值 Fig. 7 Gravity anomaly difference of different scales between SIO V32.1 and DTU10 |
| 尺度 | 最小值 | 最大值 | 平均值 | 标准差 |
| 6 | -1.94 | 1.33 | 0.12 | 0.34 |
| 7 | -1.70 | 1.77 | 0.02 | 0.41 |
| 8 | -4.59 | 8.22 | 0.01 | 0.62 |
| 9 | -11.899 | 19.03 | 0.01 | 0.96 |
| 10 | -26.63 | 44.75 | 0 | 1.50 |
2.3 基于径向基函数的多尺度分析结果
文献[18]指出球面径向基函数之间的平均间隔应大于数据分辨率的两倍,因此设置Reuter格网的分辨率为2′×2′。在确定球面径向基函数中心点的水平位置后,设置深度的上限为20 km,下限为80 km,步长为5 km,采用GCV技术确定球面径向基函数的最优深度为50 km。利用Poisson核球面径向基函数对DTU17模型重力异常进行建模,结果如图 8所示,建模残差主要在±1 mGal以内(标准差为1.27 mGal,见表 4),较大值分布较为集中,在马里亚纳群岛、海底山附近。
|
| 图 8 DTU17模型重力异常基于RBF的重构结果 Fig. 8 Reconstruction of DTU17 based on RBF |
| 方法 | 最小值 | 最大值 | 平均值 | 标准差 |
| 多尺度建模 | -7.61 | 11.65 | 0.000 | 1.18 |
| GCV方法建模 | -10.42 | 9.06 | 0.000 | 1.27 |
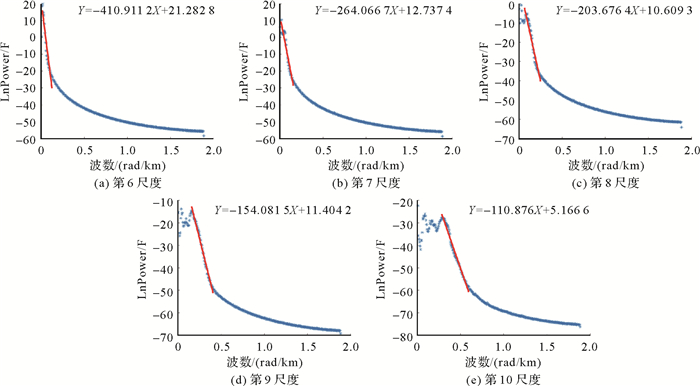
利用径向对数功率谱分析方法(式(5)—式(6))反演DTU17模型第6~10尺度重力异常对应的场源深度(图 9),分别约为205.46、132.03、101.84、77.04和55.44 km。
|
| 图 9 DTU17模型重力异常各尺度深度反演结果 Fig. 9 Inverse result of depth for different scales of DTU17 gravity anomaly model |
利用DTU17重力异常模型不同尺度反演的深度值和对应的空间分辨率(表 2)构建径向基函数,并以此实现基于径向基函数的DTU17模型重力异常多尺度分析,具体过程如下。
步骤(1):将第6尺度重力异常作为观测值,以该尺度所支持的空间分辨率174.4 km确定Reuter格网分布,基于径向对数功率谱分析反演得到第6尺度信号所对应的地质体埋深,求解该层Poisson核球面径向基函数系数的最小二乘解,并计算该层每个格网点上的重力异常。
步骤(2):从DTU17模型重力异常中扣除步骤(1)计算的重力异常,并将残余重力异常作为第2层(即132 km深度处)Poisson核球面径向基函数的观测值进行逼近。
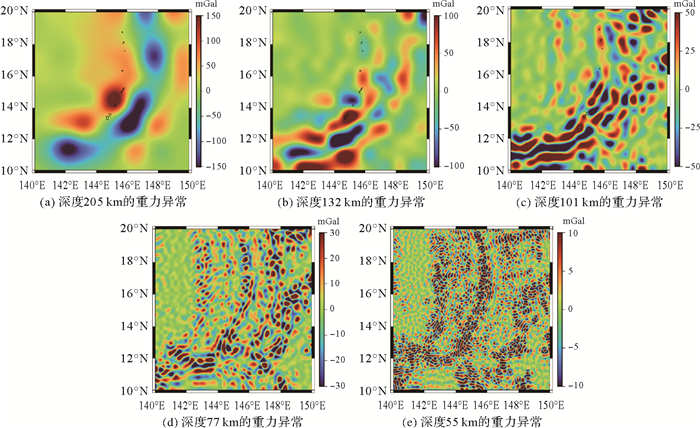
步骤(3):重复上述步骤,直至计算完不同深度处的重力异常,各层的建模结果如图 10(a)—(e)所示,DTU17模型重构效果如图 11(a)所示。
|
| 图 10 基于不同深度RBF的重力异常多尺度分析 Fig. 10 The multi-scale analysis of gravity anomaly base on the RBF in the different depth |
|
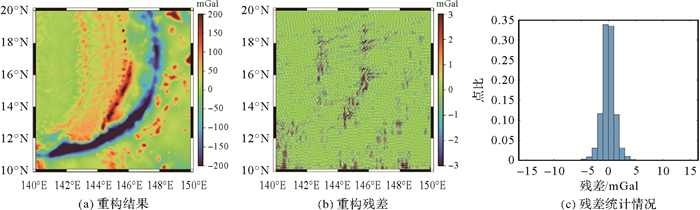
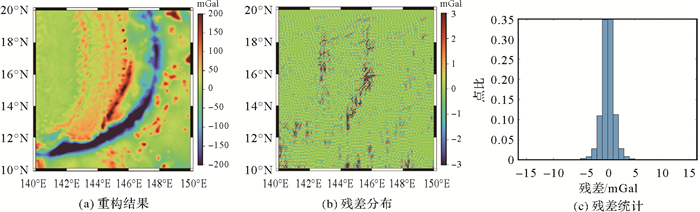
| 图 11 重力异常RBF多尺度重构结果及残差 Fig. 11 Multi-scale reconstruction and residual of gravity anomaly based on RBF |
为评估顾及不同深度、不同分辨率情况下径向基函数的重力异常多尺度分析效果,将各深度的信号叠加获得DTU17重构重力异常,计算重构残差,残差较小,标准差为1.18 mGal(表 4),略优于单一深度情况下径向基函数建模精度。
3 结论与展望球面小波具有良好的局部性和多尺度分析能力,可以提取不同空间分辨率下的地球重力场的信息。本文选取马里亚纳海沟这一典型区域,分别基于DOG球面小波函数对分辨率为1′×1′的DTU10、DTU17及SIO V32.1模型进行了多尺度分析,并尝试利用不同尺度下重力异常信号的空间分辨率和地质体深度信息实现基于径向基函数的多尺度分析,结果表明:
(1) DOG球面小波函数可以实现对重力异常的多尺度分析,同尺度下重力异常的差异可反映出不同观测数据的贡献。随着尺度减小,模型间差异增大。DTU10、DTU17模型的差异主要体现在第9、10尺度,标准差分别为1.23、1.94 mGal,主要差异分布在海岸、海沟及海底山区域,经分析发现,FES2014海潮模型分辨率的提高,Cryosat-2和Jason-1/GM观测数据的加入分别是引起第9、10尺度信号差异的主要原因;在解算方法、观测数据及重跟踪的影响下,SIO V32.1、DTU17模型间的差异与DTU10、DTU17模型差异不同,体现在第6—10各个尺度分量中,且第6尺度时,差异约为0.34 mGal,第10尺度时,差异约为1.50 mGal。
(2) 以DTU17重力异常模型为例,验证了不同深度、不同空间分辨率径向基函数多尺度分析的能力。在球面小波函数多尺度分析结果基础上,基于各尺度的空间分辨率确定Reuter格网分布,利用径向对数功率谱分析方法反演了各尺度信号对应的场源深度,以此构建径向基函数,实现深度由深到浅、空间分辨率由低到高的基于径向基函数的重力异常多尺度分析,重构精度较高,标准差为1.18 mGal,略优于单一深度情况下径向基函数建模效果,且可以解决该方法使用中通过迭代确定基函数的深度和网络设计的问题。
(3) 联合球面小波函数和径向基函数,如何充分顾及不同数据的分辨率及其频谱信息,提高不同重力数据之间的融合精度还有待进一步研究。
致谢: 感谢DTU、SIO提供的重力异常模型。
| [1] |
MARKS K M. Resolution of the Scripps/NOAA marine gravity field from satellite altimetry[J]. Geophysical Research Letters, 1996, 23(16): 2069-2072. DOI:10.1029/96GL02059 |
| [2] |
SANDWELL D T, SMITH W H F. Marine gravity anomaly from Geosat and ERS 1 satellite altimetry[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B5): 10039-10054. DOI:10.1029/96JB03223 |
| [3] |
ANDERSEN O B, KNUDSEN P. Global marine gravity field from the ERS-1 and Geosat geodetic mission altimetry[J]. Journal of Geophysical Research: Oceans, 1998, 103(C4): 8129-8137. DOI:10.1029/97JC02198 |
| [4] |
HWANG C, KAO E C, PARSONS B. Global derivation of marine gravity anomalies from Seasat, Geosat, ERS-1 and TOPEX/POSEIDON altimeter data[J]. Geophysical Journal International, 1998, 134(2): 449-459. DOI:10.1111/j.1365-246X.1998.tb07139.x |
| [5] |
张胜军, 李建成, 孔祥雪. 基于Laplace方程的垂线偏差法反演全球海域重力异常[J]. 测绘学报, 2020, 49(4): 452-460. ZHANG Shengjun, LI Jiancheng, KONG Xiangxue. Inversion of global marine gravity anomalies with vertical deflection method deduced from Laplace equation[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(4): 452-460. DOI:10.11947/j.AGCS.2020.20190108 |
| [6] |
ZHU Chengcheng, GUO Jinyun, YUAN Jiajia, et al. SDUST2021GRA: global marine gravity anomaly model recovered from Ka-band and Ku-band satellite altimeter data[J]. Earth System Science Data, 2022, 14(10): 4589-4606. DOI:10.5194/essd-14-4589-2022 |
| [7] |
WAN Xiaoyun, HAO Ruijie, JIA Yongjun, et al. Global marine gravity anomalies from multi-satellite altimeter data[J]. Earth, Planets and Space, 2022, 74: 165. DOI:10.1186/s40623-022-01720-4 |
| [8] |
孙中苗, 管斌, 翟振和, 等. 海洋卫星测高及其反演全球海洋重力场和海底地形模型研究进展[J]. 测绘学报, 2022, 51(6): 923-934. SUN Zhongmiao, GUAN Bin, ZHAI Zhenhe, et al. Research progress of ocean satellite altimetry and its recovery of global marine gravity field and seafloor topography model[J]. Acta Geodaetica et Cartographica Sinica, 2022, 51(6): 923-934. DOI:10.11947/j.AGCS.2022.20220069 |
| [9] |
GUO Jinyun, HWANG Cheinway, DENG Xiaoli. Application of satellite altimetry in marine geodesy and geophysics[J]. Frontiers in Earth Science, 2022, 10: 910562. DOI:10.3389/feart.2022.910562 |
| [10] |
SANDWELL D T, GARCIA E S, SOOFI K A, et al. Toward 1-mGal accuracy in global marine gravity from CryoSat-2, Envisat, and Jason-1[J]. The Leading Edge, 2013, 32(8): 892-899. DOI:10.1190/tle32080892.1 |
| [11] |
LI Qianqian, BAO Lifeng, WANG Yong. Accuracy evaluation of altimeter-derived gravity field models in offshore and coastal regions of China[J]. Frontiers in Earth Science, 2021, 9: 649. |
| [12] |
CHAO Nengfang, WANG Shuai, OUYANG Guichong, et al. An improved triple collocation-based integration of multiple gravity anomaly grids from satellite altimetry: contribution of ICESat-2[J]. Remote Sensing of Environment, 2023, 292: 113582. DOI:10.1016/j.rse.2023.113582 |
| [13] |
ANDERSEN O B, KNUDSEN P. The DTU17 global marine gravity field: first validation results[C]//Proceedings of 2019 International Review Workshop on Satellite Altimetry Cal/Val Activities and Applications. Cham: Springer International Publishing, 2019: 83-87.
|
| [14] |
ANDERSEN O B, KNUDSEN P, BERRY P A M. The DNSC08GRA global marine gravity field from double retracked satellite altimetry[J]. Journal of Geodesy, 2010, 84(3): 191-199. DOI:10.1007/s00190-009-0355-9 |
| [15] |
程鹏飞, 文汉江, 孙罗庆, 等. 中国大陆GPS速度场的球面小波模型及多尺度特征分析[J]. 测绘学报, 2015, 44(10): 1063-1070. CHENG Pengfei, WEN Hanjiang, SUN Luoqing, et al. The spherical wavelet model and multiscale analysis of characteristics of GPS velocity fields in China's mainland[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(10): 1063-1070. DOI:10.11947/j.AGCS.2015.20140141 |
| [16] |
蔺文奇, 文汉江, 刘焕玲, 等. 局部重力异常的球面小波多尺度信号分析[J]. 测绘科学, 2022, 47(3): 9-15. LIN Wenqi, WEN Hanjiang, LIU Huanling, et al. Spherical wavelet multiscale signal analysis of regional gravity anomaly[J]. Science of Surveying and Mapping, 2022, 47(3): 9-15. |
| [17] |
TAPE C, MUSÉ P, SIMONS M, et al. Multiscale estimation of GPS velocity fields[J]. Geophysical Journal International, 2009, 179(2): 945-971. DOI:10.1111/j.1365-246X.2009.04337.x |
| [18] |
KLEES R, TENZER R, PRUTKIN I, et al. A data-driven approach to local gravity field modelling using spherical radial basis functions[J]. Journal of Geodesy, 2008, 82(8): 457-471. DOI:10.1007/s00190-007-0196-3 |
| [19] |
TENZER R, KLEES R. The choice of the spherical radial basis functions in local gravity field modeling[J]. Studia Geophysica et Geodaetica, 2008, 52(3): 287-304. DOI:10.1007/s11200-008-0022-2 |
| [20] |
XU Ya, HAO Tianyao, LI Zhiwei, et al. Regional gravity anomaly separation using wavelet transform and spectrum analysis[J]. Journal of Geophysics and Engineering, 2009, 6(3): 279-287. DOI:10.1088/1742-2132/6/3/007 |
| [21] |
汤井田, 杨磊, 任政勇, 等. 基于小波细节信息的重力源参数估算[J]. 地球物理学进展, 2019, 34(6): 2320-2327. TANG Jingtian, YANG Lei, REN Zhengyong, et al. Gravity source parameters estimation based on wavelet details information[J]. Progress in Geophysics, 2019, 34(6): 2320-2327. |
| [22] |
TOZER B, SANDWELL D T, SMITH W H F, et al. Global bathymetry and topography at 15ArcSec: SRTM15+[J]. Earth and Space Science, 2019, 6(10): 1847-1864. DOI:10.1029/2019EA000658 |



