随着GNSS在诸如民用航空、自动驾驶、智慧城市等应用领域的扩展,其完好性监测也逐渐受到国内外学者的关注。GNSS完好性监测评估了GNSS导航定位系统提供信息的可信度,包括在系统无法用于导航时向用户发出警告的能力[1-2]。GNSS完好性监测技术起源于民航领域,目前,有3种符合国际民航组织(International Civil Aviation Organization, ICAO)标准的标准化增强系统能够提供GNSS系统的完好性服务。这3种系统分别是:地基增强系统[3](ground based augmentation system, GBAS)、星基增强系统[4](satellite based augmentation system, SBAS)和机载增强系统[5](airborne based augmentation system, ABAS)。ABAS中的接收机自主完好性监测(receiver autonomous integrity monitoring, RAIM)是一项经典技术。RAIM仅依赖于GNSS系统进行定位,利用冗余的GNSS观测量进行完好性监测。它的服务范围包括辅助导航的航路和终端区飞行阶段,以及水平导航的进近阶段。随着各国GNSS基础设施的不断完善和用户需求的不断发展,美国联邦航空局(Federal Aviation Administration, FAA)提出了高级接收机自主完好性监测(advanced RAIM, ARAIM)作为传统RAIM的技术升级,以满足垂直导航性能LPV-200的需求。这一技术充分利用了当前GNSS系统多频多星座的特性,并结合地面监测站提供的完好性支持信息(integrity support message, ISM)来提供服务[6-8]。
GNSS完好性监测依赖于准确的函数模型和随机模型。随机模型的准确构建相比于函数模型更加困难,因为难以精确确定观测值的方差-协方差矩阵以合理描述观测值的随机特性[9-10]。ARAIM的随机模型通常由3部分组成,包括卫星端(卫星星历与钟差)、信号传播端(电离层与对流层延迟),以及接收机端(码噪声与多路径)的噪声项。其中,接收机端噪声项的随机模型通常使用RTCA在最低运行性能规范(minimum operational performance standards, MOPS)中推荐的常系数高度角模型,只能反映民航飞行环境下符合民航特定标准的GNSS接收机噪声特性[11]。然而,在不同应用场景中,接收机软、硬件和应用环境通常不符合ARAIM标准规范,且存在显著的多样性,若仍采用固化的常系数随机模型,难以保证ARAIM算法的有效性。因此,ARAIM算法若想扩展至其他应用,首要需研究随机模型的自适应精化方法。当存在足够多的先验观测信息时,可利用方差分量估计(variance component estimation, VCE)构建更符合观测值噪声特性的随机模型。方差分量估计方法众多,包括最小范数二次无偏估计(minimum norm quadratic unbiased estimator, MINQUE)、最小二乘方差分量估计(least-squares variance component estimation, LS-VCE)等[10, 12-15]。其中,LS-VCE将函数模型和随机模型通过最小二乘估计准则统一处理,操作简单灵活,实用性强[12, 16]。
本文基于LS-VCE提出了一种ARAIM接收机噪声项随机模型精化的方法。通过随机模型可靠性检验确定了随机模型精化所需的数据集及结果的准确性。对比了随机模型精化前后ARAIM的效果,进一步验证随机模型精化对于在不同应用下提升ARAIM完好性监测能力的必要性。使用了GRACE-FO C星2019年12月2日至2019年12月17日的星载GNSS观测数据进行验证。GRACE(Gravity Recovery and Climate Experiment)系列卫星由美国国家航空航天局(National Aeronautics and Space Administration, NASA)与德国航空中心(German Aerospace Center, DLR)共同发射,是通过精确地测量地球重力场从而研究地球的水资源、地质及气候的低轨卫星之一[17]。试验数据分为后处理部分(前12 d)及预报部分(后4 d)。试验的大致流程为:①利用后处理部分的数据基于LS-VCE进行接收机项随机模型精化得到GRACE-FO星载GNSS接收机的高度角模型并通过可靠性检验选择合适的拟合数据集。②分别使用精化前后的随机模型对拟合数据集及预报数据集进行ARAIM算法验证,并评估随机模型精化前后ARAIM的效果。
1 原理 1.1 最小二乘方差分量估计基本原理线性方差-协方差分量模型如下
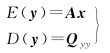 (1)
(1)
其中
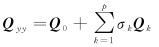 (2)
(2)
式中,E(·)和D(·)分别表示期望和方差符号;x是待估参数;Qyy是观测值的方差-协方差矩阵;Q0为方差-协方差分量矩阵中已知的部分;σk(k=1, 2, …, p)是Qyy中的矩阵元素;Qk为方差-协方差分量的定位矩阵,功能在于确定矩阵中要计算的方差所处的位置。
由加权最小二乘准则得到参数估值,以及观测值的改正数为
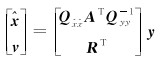 (3)
(3)
由误差传播定律可得,参数估值和改正数的数学期望和方差-协方差矩阵为
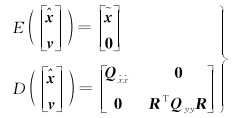 (4)
(4)
式中,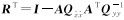
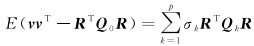 (5)
(5)
式中,左侧期望算子内的矩阵为对称方阵,此矩阵方程由r2个标量观测方程组成,r为多余观测量个数,将等式两边取半向量化算子vh(·),可得LS-VCE的线性模型为
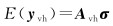 (6)
(6)
式中,yvh=vh(vvT-RTQ0R);Avh=[vh(RTQ1R), vh(RTQ2R), …, vh(RTQpR)];σ=[σ1, σ2, …, σp]T。
式(6)的加权最小二乘估值为
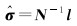 (7)
(7)
式中,N=AvhTWvhAvh;l=AvhTWvhyvh。在LS-VCE理论中,权矩阵Wvh有不同的取法,本文将使用其中一种特殊的权矩阵[18]
 (8)
(8)
式中,D为复制矩阵,作用是将半向量算子转化为向量算子;Wy为观测值的权矩阵Qyy-1;⊗为克罗内克积。由向量、半向量化算子,克罗内克积和矩阵的迹的性质,vh(S)=D+ vec(S),tr(UVST)=vec(T)T(ST⊗U)vec(VT)可知,此时N、l矩阵中的元素为
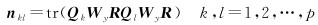 (9)
(9)
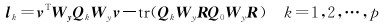 (10)
(10)
式中,k、l分别为矩阵元素所在的行数和列数,则可以求得方差-协方差分量。
1.2 随机模型精化及可靠性检验影响完好性监测可用性和有效性的关键在于随机模型的准确度。完好性监测中故障探测与排除的核心是构造符合实际情况的检验统计量,而这些检验统计量对随机模型十分敏感,所以构建准确的随机模型是有效进行故障探测与排除的前提[9, 19]。此外,为了评估随机模型精化的效果与合理性,需对随机模型精化的结果进行可靠性检验[20]。
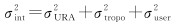 (11)
(11)
式中,σURA2为卫星星历和钟差误差的方差;σtropo2为残余对流层延迟误差的方差;σuser2为接收机噪声的方差。由于使用了无电离层组合消除了电离层一阶项的影响,所以在随机模型中忽略了电离层项。
卫星端误差σURA2,包括卫星轨道标准差σorbit和钟差标准差σclk,表达式为
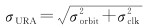 (12)
(12)
由于民用航空ARAIM使用的是广播星历[22],所以在应用精密星历时需要重新定义其随机模型,表 1为IGS官方公布的各种轨道和钟差产品的精度[23],若使用其某一类的产品,卫星端的标准差可由表 1对应得到。
| 产品 | 类型 | 精度 |
| 最终 | 轨道/钟差 | ~2 cm/~75 ps; 20 ps |
| 快速 | 轨道/钟差 | ~2.5 cm/~75 ps; 25 ps |
| 超快速(观测部分) | 轨道/钟差 | ~3 cm/~150 ps; 50 ps |
| 超快速(预测部分) | 轨道/钟差 | ~5 cm/~3 ns; 1500 ps |
| 实时 | 轨道/钟差 | ~5 cm/~300 ps; 120 ps |
对于对流层延迟项σtropo2,在ARAIM用户基准算法中,经模型改正后的残余对流层延迟误差的标准差建模为
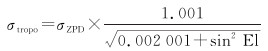 (13)
(13)
式中,σZPD为天顶方向的残余对流层误差的标准差;El为卫星高度角;分式部分为投影函数[24]。由于GRACE-FO卫星的轨道高度约为500 km[17],处于对流层的上方,所以可以忽略对流层的影响。
对于接收机噪声项σuser2,针对民航飞行应用,通常在ARAIM中使用常系数高度角模型
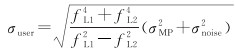 (14)
(14)
式中,fL1和fL2分别为L1频段和L2频段的频率;σMP为多路径误差;σnoise为接收机噪声误差,具体形式为
 (15)
(15)
然而,在不同环境的定位应用中,高度角模型必须重新定义以提高监测异常观测值的能力。本文利用LS-VCE得到的方差对式(16)高度角模型[25]中的系数a、b进行拟合,以获得精化的接收机端随机模型
 (16)
(16)
随机模型的可靠性可以通过检验样本组与预设概率密度函数的匹配程度来评估[20]。本文构造了基于位置参数解向量及其估计方差-协方差阵的统计量T
 (17)
(17)
式中,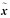
 (18)
(18)
式中,hbinCount为概率分布直方图的组数;ycentor, i代表概率分布直方图中每组的概率;ychi2, i代表每组组距中点对应的χ2(3)的概率密度函数值。ind指标越小,代表统计量T越符合χ2(3)。
1.3 完好性监测 1.3.1 故障探测与排除故障探测与排除是完好性监测的重要任务之一[26],在ARAIM用户基准算法中,故障探测与排除的方法采用解分离的方式。解分离的核心思想是通过剔除故障卫星后进行容错子集定位解算,然后对容错子集解与无故障全集解的差值进行连续性风险检验,如果此检验量超过阈值,则代表该子集的是一个出现故障的子集,未包含在子集解算的卫星存在故障,需要进行排除。具体算法步骤如下:
(1) 无故障全集与容错子集定位。由最小二乘准则得到的定位解的参数估计值为
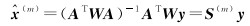 (19)
(19)
式中, m为故障子集的索引,当m=0时,解算结果为无故障全集定位解;设计矩阵A为一个雅可比矩阵,矩阵大小为Nsat×(3+Nconst),Nsat为参与定位解算的卫星数量,Nconst为参与定位解算的星座数量;y为伪距的残差,权矩阵W的定义如下
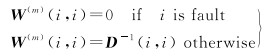 (20)
(20)
即将第m个故障子集中的故障卫星的权值置零,D为随机模型的方差协方差矩阵。
(2) 解分离检验。使用每个容错子集的定位解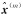
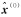
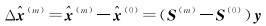 (21)
(21)
并计算其方差可得
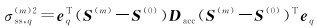 (22)
(22)
式中,q∈{1, 2, 3},分别代表 3个方向的分量;eq为一维向量,其中第q个元素为1,其余为0。通过解分离检验量的方差,可以计算检验阈值
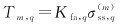 (23)
(23)
式中,Kfa, q由连续性风险概率得出,每个故障子集都被分配了连续性风险概率,而这些子集的连续性风险概率又被分配到了3个方向上,其定义式为
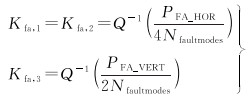 (24)
(24)
式中,PFA_HOR与PFA_VERT为ARAIM用户基准算法中定义的水平及垂直连续性风险概率,大小分别为9×10-8和3.9×10-6[11];Nfaultmodes为故障模式的数量;Q(·)为标准正态分布概率密度函数。容错子集是否存在异常的检验方式如下
 (25)
(25)
每一个容错子集的定位解和无故障全集定位解构成的距离检验量都需要在3个方向进行检验且3个方向的检验都通过时,才可以认为该故障子集无故障,否则该故障子集发生了故障,其对应的故障卫星需要被排除。
1.3.2 保护级计算在实际应用中,真实定位误差不可知,因此需计算保护级以衡量超过报警限值的完好性风险。其中,报警限值指系统不发出警报时允许的真实定位误差的上界;完好性风险指真实定位误差超过报警限值的概率[5]。保护级通常在位置域分解为水平保护级和垂直保护级,并分别进行计算。其中,水平保护级表示给定完好性风险下水平位置误差的边界;类似地,垂直保护级代表垂直位置误差的边界,其计算公式如下
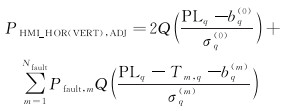 (26)
(26)
 (27)
(27)
式中,PHMI_HOR(VERT), ADJ为先验水平(垂直)完好性风险,其数值由具体应用领域的规范给出。在ARAIM用户基准算法中,水平完好性风险通常取10-8,垂直完好性风险通常取9×10-8[11]。q=1,2表示水平分量下标标识,q=3表示垂直分量下标标识;PLq为保护级分量;bq(m)为卫星标称偏差在定位域的投影;σq(m)为定位解的标准差;Pfault, m为m阶故障发生的概率;PHMI为总的完好性风险;PHMIHOR(VERT)为水平(垂直)方向上分配的完好性风险,Psat not monitored和Pconst not monitored分别为卫星和星座未监测风险概率。垂直保护级和水平保护级分别表示为
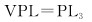 (28)
(28)
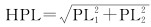 (29)
(29)
式(26)中未知参数为待求解的保护级分量PLq,可利用数值计算二分法求解。若当前历元的水平保护级大于水平报警限值或垂直保护级大于垂直报警限值时,完好性监测系统将被宣布为不可用;当系统声明可用,且定位误差超过保护级但未超过报警限值时,即发生误导信息(misleading information, MI)事件;当系统声明可用,且定位误差超过报警限值时,即发生危险误导信息(hazardously misleading information, HMI)事件。
2 试验本文试验选取GRACE-FO C星2019年12月2日至2019年12月17日的实测数据(包含星载GPS接收机的观测数据,GRACE-FO卫星精密轨道的数据),使用IGS分析中心给出的事后精密星历和钟差产品计算GNSS卫星的精密轨道和钟差,使用双频无电离层组合消除电离层延迟的一次项的影响,忽略对流层延迟的影响。试验数据分为后处理部分(前12 d)及预报部分(后4 d)。
由于忽略了对流层延迟的影响,式(11)中σtropo2=0。式(2)中的Q0为卫星端的误差,即将σURA2作为LS-VCE中的已知部分,估计接收机端误差项的方差。由于方差分量估计利用多余观测量信息估计方差,因此可将后处理部分的GRACE-FO卫星精密轨道的数据作为参考值代入方程,以减少未知参数,从而提升方差分量估计的准确性(上述做法并不会影响预报部分数据完好性监测的实时性)。将错误估计产生的小于等于0的方差剔除,再利用高度角模型将标准差与高度角进行拟合,参与拟合的历元满足3个方向的定位误差皆小于3倍标准差的准则,最终得到高度角模型的系数值。
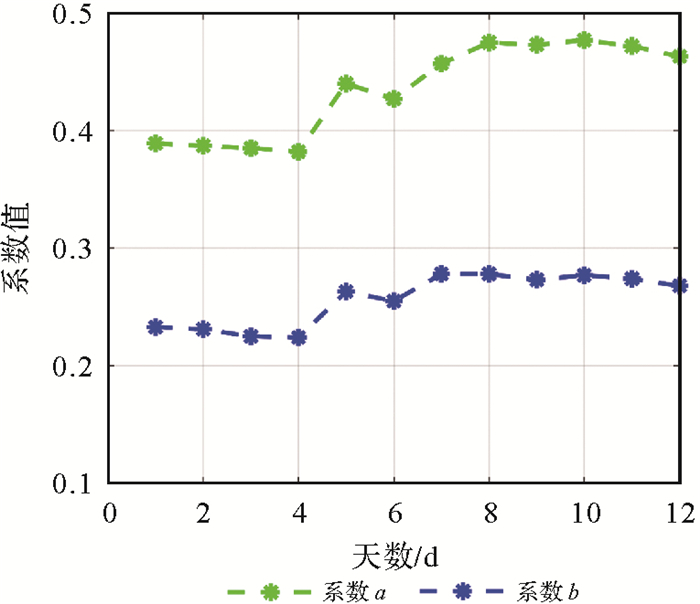
图 1展示了依据式(16)的高度角模型系数拟合结果,横轴的天数表示根据前i天后处理数据得到的结果,其中i∈{1, 2, …, 12}。可以发现,系数a、b呈现大致相同的变化规律,前1 d至前7 d变化波动较大,在前8 d后趋于稳定。这是由于数据量少会使拟合效果不稳定,当数据量大时拟合系数便会趋于稳定。表 2列出了系数a、b的具体值。为了确定合适的拟合数据样本量,分别对上述随机模型精化结果进行随机模型可靠性检验,统计结果如表 2所示。由表 2可知,前10 d的ind指标最小,表明统计量T更加符合自由度为3的卡方分布。所以选择前10 d的后处理数据作为拟合数据集使用相应的高度角模型系数。
|
| 图 1 高度角模型拟合系数 Fig. 1 LS-VCE fitting curve |
| 后处理数据天数/d | LS-VCE拟合系数值 | ind | |
| a | b | ||
| 1 | 0.389 | 0.233 | 3.43 |
| 2 | 0.387 | 0.231 | 3.38 |
| 3 | 0.385 | 0.225 | 3.28 |
| 4 | 0.382 | 0.224 | 3.32 |
| 5 | 0.440 | 0.263 | 2.28 |
| 6 | 0.427 | 0.255 | 2.48 |
| 7 | 0.457 | 0.278 | 2.00 |
| 8 | 0.475 | 0.278 | 1.53 |
| 9 | 0.473 | 0.273 | 1.46 |
| 10 | 0.477 | 0.277 | 1.43 |
| 11 | 0.472 | 0.274 | 1.49 |
| 12 | 0.463 | 0.268 | 1.60 |
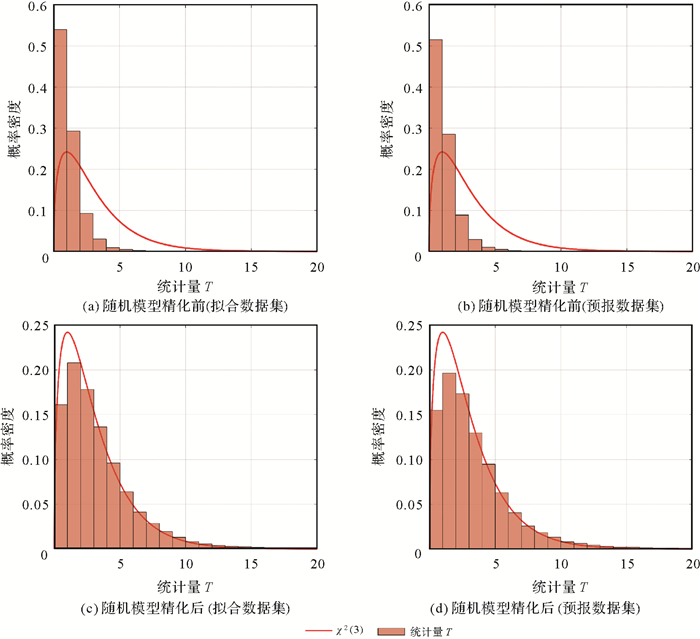
图 2显示了拟合数据集(图 2(a)、图 2(c))与预报数据集(图 2(b)、图 2(d))的随机模型可靠性检验的结果。其中柱状体是统计量T的概率分布直方图,红色曲线为自由度为3的卡方分布的概率密度函数曲线。图 2(a)—图 2(b)显示,在随机模型精化之前,柱状体的分布和预设的概率密度函数曲线具有较大偏差,统计量T的ind指标为8.25(拟合数据集)和7.77(预报数据集)。此时,统计量T与χ2(3)的概率密度函数匹配程度较低。图 2(c)—图 2(d),经过LS-VCE精化随机模型后与χ2(3)的概率密度函数匹配程度显著提高,其ind指标分别为1.43(拟合数据集)和1.66(预报数据集)。由式(17)可知,统计量T受定位误差及其方差阵的影响。随机模型精化前,统计量T分布在左侧,表明精化前的方差协方差矩阵定义过于保守,精化后的随机模型更加准确地反映了观测噪声水平,而且拟合数据集和预测数据集均有这样的趋势,验证了随机模型精化的有效性。
|
| 图 2 随机模型精化前后统计量T的概率分布 Fig. 2 Probability distribution of T before and after stochastic model refinement |
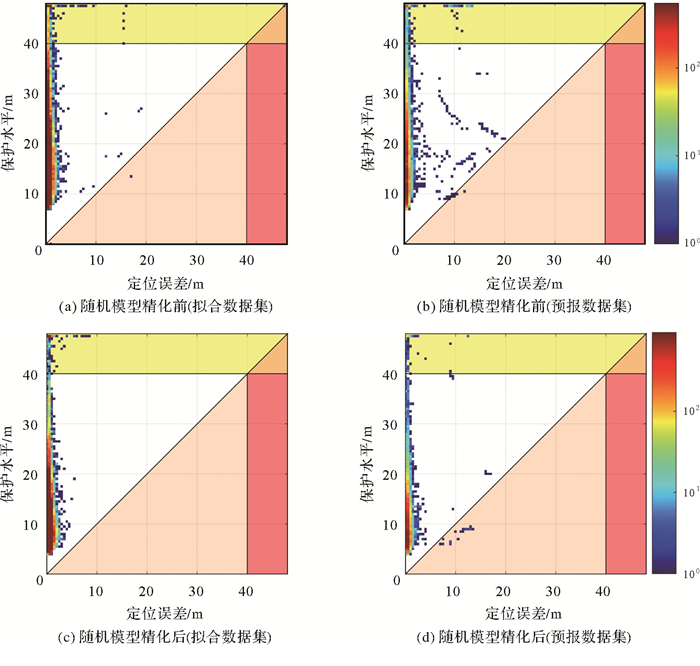
图 3展示了随机模型精化前后的水平保护级与水平定位误差绘制的斯坦福图。斯坦福图用于解释和说明大多数完好性事件及其关系,以及评估定位系统性能。在斯坦福图中,每个历元的定位误差和保护级在图中绘制为一个点,横轴为定位误差,纵轴为保护级,水平分量和垂直分量分别单独绘制。斯坦福图可以快速查看是否发生了完好性事件,正常定位区域(白色)和发生MI事件区域(粉色)由对角线分隔,红色区域表示发生HMI事件,而且斯坦福图还可以评估系统的可用性,由纵坐标大于报警限值的区域(黄色、橙色)表示。图中的颜色条代表散点的集中程度。为了评估随机模型精化对完好性可用性及各种完好性事件发生概率的影响,本文暂且将水平与垂直告警门限分别设置为40 m与35 m[11]。表 3列出了随机模型精化前后的各项指标,包括平均保护级、系统可用性、MI事件发生历元数和HMI事件发生历元数。通过对比图 3(a)、图 3(b)和图 3(c)、图 3(d)的黄色区域散点可以看出,无论是拟合数据集或是预报数据集,在随机模型精化后完好性监测系统不可用的历元散点明显减少。对于整体散点的分布在随机模型精化后都呈现向下集中的趋势,这表明随机模型精化后保护级总体降低,系统可用性显著升高。表 3进一步显示,随机模型精化后的拟合数据集与预报数据集的平均水平保护级分别降低了7.78和7.68 m,而平均垂直保护级分别降低了6.39和6.24 m,完好性监测系统可用性分别提升了4.6%和5.3%。上述结果表明,随机模型精化可以有效降低水平与垂直保护级,提高完好性监测系统的可用性。
|
| 图 3 随机模型精化前后的水平斯坦福图 Fig. 3 Horizontal Stanford diagram before and after stochastic model refinement |
| 数据集 | 随机模型精化前 | 随机模型精化后 | |||||||||
| 平均HPL/m | 平均VPL/m | 可用性/(%) | MI事件历元数 | HMI事件历元数 | 平均HPL/m | 平均VPL/m | 可用性/(%) | MI事件历元数 | HMI事件历元数 | ||
| 拟合数据集 | 18.70 | 15.69 | 93.6 | 6 | 0 | 10.92 | 9.30 | 98.2 | 132 | 0 | |
| 预报数据集 | 10.92 | 15.53 | 93.3 | 63 | 0 | 10.94 | 9.29 | 98.6 | 84 | 0 | |
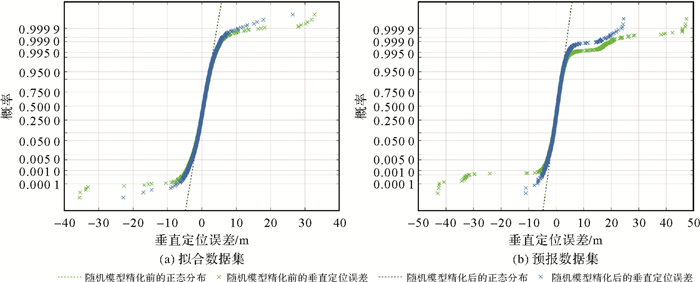
图 4展示了随机模型精化前后垂直定位误差分布的概率图,图中蓝色散点和绿色散点分别代表随机模型精化前后。虚线为正态分布概率图,散点越靠近虚线分布,说明此组数据越符合正态分布。表 4列出了随机模型精化前后解分离故障探测与排除后的均方根误差(root mean square error, RMSE)及图 4中0.990 0、0.999 0及0.999 9的概率下对应的定位误差。由图 4可以看出,拟合数据集和预报数据集都呈现出相同的规律:相比于绿色散点,蓝色散点的分布更靠近虚线,而且离群值明显较少。表 4显示,随机模型精化后,拟合数据集在0.990 0、0.999 0及0.999 9的概率下的定位误差分别降低了0.05、2.63和19.84 m;预报数据集在0.990 0、0.999 0及0.999 9的概率下的定位误差分别降低了1.93、27.22和22.70 m。上述分析表明,随机模型精化对于整体的数据解算精度提升有限,但可以显著降低小概率条件下的极端定位误差。这表明随机模型精化有效提升了ARAIM解分离故障探测与排除的能力。
|
| 图 4 随机模型精化前后垂直定位误差分布的概率图 Fig. 4 Vertical position error probability plot before and after stochastic model refinement |
| 数据集 | 随机模型精化前 | 随机模型精化后 | |||||||
| RMSE | 0.990 0概率下 | 0.999 0概率下 | 0.999 9概率下 | RMSE | 0.990 0概率下 | 0.999 0概率下 | 0.999 9概率下 | ||
| 拟合数据集 | 1.35 | 4.03 | 6.61 | 33.08 | 1.27 | 3.98 | 6.18 | 13.24 | |
| 预报数据集 | 2.07 | 6.32 | 31.61 | 47.03 | 1.43 | 4.39 | 19.12 | 24.33 | |
由图 3、图 4和表 4的结果可知,随机模型精化可以提升ARAIM的完好性监测能力,从而使ARAIM算法适用于更多领域。一方面,随机模型精化可以有效降低保护级从而提升系统完好性监测的可用性;另一方面,随机模型精化可以提升ARAIM解分离故障探测与排除的能力,降低小概率条件下的极端定位误差。
3 结论ARAIM的两个主要任务是故障探测与排除,以及计算保护级判断系统可用性。为了将只满足民航特殊规范的ARAIM算法推广应用至更多领域,需对其接收机噪声项随机模型进行自适应精化,使之能够准确描述各类型GNSS接收机的噪声特性。本文基于LS-VCE提出了一种ARAIM随机模型精化方法,并选取GRACE-FO C星2019年12月2日至2019年12月17日的实测数据进行验证,结果表明:
(1) 随机模型精化可有效降低ARAIM保护级进而提升ARAIM可用性。在随机模型精化后,拟合数据集和预报数据集的平均水平保护级分别降低了7.78和7.68 m,平均垂直保护级分别降低了6.39和6.24 m,ARAIM可用性分别提升了4.6%和5.3%。
(2) 随机模型精化可提升ARAIM解分离故障探测与排除的有效性。随机模型精化后,拟合数据集和预报数据集的RMSE虽然并未发生显著变化,但是在99.99%概率下的定位误差分别下降了19.84和22.70 m。总之,随机模型精化是将ARAIM扩展至其他应用领域的必要步骤。一方面,随机模型精化可以提升ARAIM的故障探测与排除能力,降低小概率条件下的极端定位误差;另一方面,随机模型精化可有效降低保护级,从而提升系统的可用性。
| [1] |
牛飞. GNSS完好性增强理论与方法研究[D]. 郑州: 信息工程大学, 2008. NIU Fei. Theory and technique on GNSS integrity augment[D]. Zhengzhou: Information Engineering University, 2008. |
| [2] |
苏先礼. GNSS完好性监测体系及辅助性能增强技术研究[D]. 上海: 上海交通大学, 2013. SU Xianli. The research on GNSS integrity monitoring theory and assisted performance enhancement technique[D]. Shanghai: Shanghai Jiao Tong University, 2013. |
| [3] |
JIANG Yiping, MILNER C, MACABIAU C. Code carrier divergence monitoring for dual-frequency GBAS[J]. GPS Solutions, 2017, 21(2): 769-781. DOI:10.1007/s10291-016-0567-4 |
| [4] |
刘慧芹. 广域差分GPS完好性监测研究[D]. 上海: 同济大学, 2007. LIU Huiqin. The research on integrity of wide area differential GPS system[D]. Shanghai: Tongji University, 2007. |
| [5] |
ZHU Ni, MARAIS J, BETAILLE D, et al. GNSS position integrity in urban environments: a review of literature[J]. IEEE Transactions on Intelligent Transportation Systems, 2018, 19(9): 2762-2778. DOI:10.1109/TITS.2017.2766768 |
| [6] |
董開琳. GPS/BDS ARAIM适航测试技术研究[D]. 天津: 中国民航大学, 2020. DONG Kailin. Research on GPS/BDS ARAIM airworthiness test technology[D]. Tianjin: Civil Aviation University of China, 2020. |
| [7] |
罗思龙. GNSS用户级完好性监测算法理论、性能评估及优化研究[D]. 西安: 长安大学, 2019. LUO Silong. Research on theory, performance assessment and optimization of GNSS user-based integrity monitoring algorithm[D]. Xi'an: Changan University, 2019. |
| [8] |
孟骞. 北斗导航接收机信号捕获及完好性监测关键技术研究[D]. 南京: 南京航空航天大学, 2018. MENG Qian. Research on BeiDou navigation receiver signal acquisition and integrity monitoring[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2018. |
| [9] |
LI Bofeng, LOU Lizhi, SHEN Yunzhong. GNSS elevation-dependent stochastic modeling and its impacts on the statistic testing[J]. Journal of Surveying Engineering, 2016, 142(2): 04015012-1-04015012-7. |
| [10] |
LI Bofeng, SHEN Yunzhong, LOU Lizhi. Efficient estimation of variance and covariance components: a case study for GPS stochastic model evaluation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(1): 203-210. DOI:10.1109/TGRS.2010.2054100 |
| [11] |
BLANCH J, WALKER T, ENGE P, et al. Baseline advanced RAIM user algorithm and possible improvements[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(1): 713-732. DOI:10.1109/TAES.2014.130739 |
| [12] |
RAO C R. Estimation of variance and covariance components—MINQUE theory[J]. Journal of Multivariate Analysis, 1971, 1(3): 257-275. DOI:10.1016/0047-259X(71)90001-7 |
| [13] |
赵俊, 郭建锋. 方差分量估计的通用公式[J]. 武汉大学学报(信息科学版), 2013, 38(5): 580-583, 588. ZHAO Jun, GUO Jianfeng. An universal formula of variance component estimation[J]. Geomatics and Information Science of Wuhan University, 2013, 38(5): 580-583, 588. |
| [14] |
AMIRI-SIMKOOEI A R, TEUNISSEN P J G, TIBERIUS C C J M. Application of least-squares variance component estimation to GPS observables[J]. Journal of Surveying Engineering, 2009, 135(4): 149-160. DOI:10.1061/(ASCE)0733-9453(2009)135:4(149) |
| [15] |
鲁铁定, 徐华卿, 贺小星, 等. 等价条件闭合差最小范数分量的GNSS坐标时间序列噪声估计[J]. 武汉大学学报(信息科学版), 2023, 48(8): 1331-1339. LU Tieding, XU Huaqing, HE Xiaoxing, et al. GNSS coordinate time series noise estimation based on minimum norm component of closure error under equivalent conditions[J]. Geomatics and Information Science of Wuhan University, 2023, 48(8): 1331-1339. |
| [16] |
AMIRI-SIMKOOEI A R, ZANGENEH-NEJAD F, ASGARI J. Least-squares variance component estimation applied to GPS geometry-based observation model[J]. Journal of Surveying Engineering, 2013, 139(4): 176-187. DOI:10.1061/(ASCE)SU.1943-5428.0000107 |
| [17] |
许厚泽. 卫星重力研究: 21世纪大地测量研究的新热点[J]. 测绘科学, 2001, 26(3): 1-3. XU Houze. Satellite gravity missions-new hotpoint in geodesy[J]. Science of Surveying and Mapping, 2001, 26(3): 1-3. |
| [18] |
TEUNISSEN P J G, AMIRI-SIMKOOEI A R. Least-squares variance component estimation[J]. Journal of Geodesy, 2008, 82(2): 65-82. DOI:10.1007/s00190-007-0157-x |
| [19] |
LI Bofeng. Stochastic modeling of triple-frequency BeiDou signals: estimation, assessment and impact analysis[J]. Journal of Geodesy, 2016, 90(7): 593-610. DOI:10.1007/s00190-016-0896-7 |
| [20] |
BORKO A, EVEN-TZUR G. Stochastic model reliability in GNSS baseline solution[J]. Journal of Geodesy, 2021, 95(2): 20. DOI:10.1007/s00190-021-01472-1 |
| [21] |
ZHANG Yabin, WANG Li, FAN Lihong, et al. MHSS ARAIM algorithm combined with gross error detection[J]. Journal of Geodesy and Geoinformation Science, 2020, 3(1): 36-44. |
| [22] |
WALTER T, BLANCH J. Characterization of GNSS clock and ephemeris errors to support ARAIM[C]//Proceedings of 2015 ION Pacific PNT Meeting. Honolulu: ION, 2015: 920-931.
|
| [23] |
孙楠, 杨玲, 喻杨康. ARAIM随机模型精化对完好性监测可用性的影响分析[C]//第十三届中国卫星导航年会论文集——S03卫星导航系统与增强. 北京: 中国卫星导航系统管理办公室学术交流中心, 2022. SUN Nan, YANG Ling, YU Yangkang. Analysis of the impact of ARAM stochastic model refinement on the availability of integrity monitoring[C]//Proceedings of the 13th China Satellite Navigation Conference-S03 Satellite Navigation System and Enhancement. Beijing: Academic Exchange Center of China Satellite Navigation System Management Office, 2022. |
| [24] |
YANG Ling, WANG Jinfang, LI Haojun, et al. Global assessment of the GNSS single point positioning biases produced by the residual tropospheric delay[J]. Remote Sensing, 2021, 13(6): 1202. DOI:10.3390/rs13061202 |
| [25] |
ZHANG Baocheng, HOU Pengyu, LIU Teng, et al. A single-receiver geometry-free approach to stochastic modeling of multi-frequency GNSS observables[J]. Journal of Geodesy, 2020, 94(4): 37. DOI:10.1007/s00190-020-01366-8 |
| [26] |
EL-MOWAFY A. On detection of observation faults in the observation and position domains for positioning of intelligent transport systems[J]. Journal of Geodesy, 2019, 93(10): 2109-2122. DOI:10.1007/s00190-019-01306-1 |


