2. 自然资源部大地测量数据处理中心,陕西 西安 710054;
3. 中国地质调查局自然资源航空物探遥感中心,北京 100083
2. Geodetic Data Processing Centre of Ministry of Natural Resources, Xi'an 710054, China;
3. China Aero Geophysical Survey and Remote Sensing Center for Natural Resources, Beijing 100083, China
2019—2020年期间,我国完成2020珠峰高程测量,与尼泊尔合作确定了基于国际高程参考系统的最新珠峰雪面正高,并于2021年12月8日共同宣布。中国和尼泊尔有各自国家的法定高程基准,为实现共同宣布唯一珠峰高程,双方决定:根据2015年国际大地测量协会关于国际高程参考系统定义和实现的决议[1],在珠峰地区实现国际高程参考系统,作为珠峰高程的起算基准。因此,建立基于国际高程参考系统的高精度珠峰区域大地水准面模型、精密确定珠峰峰顶大地水准面差距,是2020珠峰高程测量的关键问题。
大地水准面确定需要区域内密集分布的重力数据,珠峰及周边地区是世界最高海拔区域,地形地貌复杂险峻,严寒缺氧、人迹罕至,大部分区域无法开展地面重力测量,特别是珠峰邻近区域,地形和重力场变化剧烈,几乎是地面重力数据空白,严重制约了珠峰区域大地水准面模型的精度。为解决重力数据稀少/空白问题,此次珠峰测量首次在珠峰区域开展高精度航空重力测量,并首次采集珠峰峰顶地面重力数据,这为构建高精度珠峰区域大地水准面模型奠定了数据基础。
珠峰及周边地区具备地面和航空重力数据可供使用,两类数据具有不同的空间分布、信号频谱和误差特性,揭示不同波段(或频谱)的地球重力场信息。航空重力数据主要贡献中短波重力场信息,地面重力数据则主要反映短波信号。如何实现航空和地面重力数据优化融合处理是高精度重力大地水准面确定的难点问题[2-8]。
目前联合航空和地面重力数据解算大地水准面的方法主要分为3类:
第一类方法是先将航空重力数据从飞行高度处向下延拓至地面或大地水准面,与地面重力数据融合得到格网平均重力异常,再利用Stokes积分或最小二乘配置计算大地水准面[5, 9-12]。该方法是两步法,需要对航空重力数据进行两次处理,每一次处理都会引入边界效应,造成数据资源浪费,并且数据联合时未按照每种类型数据的频谱和误差特性配权。
第二类方法是最小二乘配置。该方法可一步联合航空和地面重力数据解算大地水准面[10, 13],其优点是能够同时容纳不同类型和空间分布的重力数据求解扰动位及其泛函。最小二乘配置涉及高阶协方差矩阵组建和大型矩阵求逆计算,对于大范围区域,计算工作量庞大,这一缺陷制约了该方法的普遍应用。
第三类方法是谱组合法[14-15]。该方法从重力场参量之间的解析关系出发,将重力场参量按阶作谱分解,依据最小二乘原理确定各类数据的谱权,按谱权由各类数据通过大地测量积分解析关系求解重力场参量,可一步联合航空和地面重力数据解算大地水准面。谱组合引入谱权,考虑了不同类型数据之间频谱重叠的情况,积分求解避免了大型矩阵求逆计算,计算效率高。谱组合法的关键在于合理确定各类重力数据的谱权,即准确估计各类重力数据的误差阶方差[6, 16]。
本文利用谱组合方法联合航空和地面重力数据建立珠峰区域重力似大地水准面模型,并确定基于国际高程参考系统的珠峰峰顶大地水准面差距,在珠峰地区实现国际高程参考系统。
1 数学模型基于国际高程参考系统的珠峰峰顶大地水准面差距N为
 (1)
(1)
式中,ζ为峰顶高程异常,由珠峰区域重力似大地水准面模型插值计算得到;Δ为高程异常转换为大地水准面差距的改正项;N0为基于国际高程参考系统的大地水准面差距零阶项。
1.1 谱组合方法珠峰地区重复覆盖有地面和航空重力数据,可利用谱组合方法联合地面和航空重力数据建立珠峰区域重力似大地水准面模型。区域内某点的高程异常可分解为地面和航空重力数据贡献2个部分
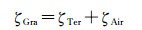 (2)
(2)
式中,ζGra为高程异常;ζTer为地面重力数据的高程异常贡献;ζAir为航空重力数据的高程异常贡献。
采用移去-计算-恢复技术,优选地球重力场模型作为参考重力场,利用残余地形模型(RTM)方法由高分辨率数字高程模型(DEM)计算高频重力地形效应[17],地面和航空重力数据的高程异常贡献可进一步分解,则式(2)改写为
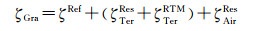 (3)
(3)
式中, ζRef为利用参考重力场模型计算的参考高程异常;ζTerRes为由残余地面重力异常ΔgTerRes(如式(6)所示)计算的残余高程异常;ζTerRTM为地面重力异常RTM地形效应对应的高程异常;ζAirRes为由残余航空重力扰动(式(11))计算的残余高程异常。
利用Molodensky解析延拓法将残余地面重力异常ΔgTerRes从地面解析延拓至点水准面后[18],采用带谱权的Stokes积分计算地面重力数据贡献的残余高程异常ζTerRes
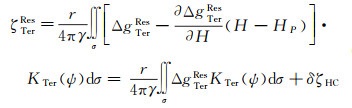 (4)
(4)
式中,r为计算点地心距离;HP和H分别为计算点和流动点的地形高度;δζHC表示高程异常的解析延拓改正项;KTer(ψ)为带谱权的Stokes核函数,写为
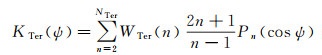 (5)
(5)
式中,ψ为计算点与流动点的球面角距;NTer为地面重力异常格网对应的最大展开阶数;WTer(n)为第n阶地面重力谱权。
式(4)中的残余地面重力异常ΔgTerRes按照式(6)计算
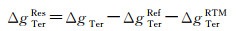 (6)
(6)
式中,ΔgTer为地面重力异常;ΔgTerRef为由参考重力场模型计算的参考地面重力异常;ΔgTerRTM为采用RTM方法由高分辨率DEM计算的地面重力异常高频地形效应。
式(4)中的高程异常解析延拓改正项δζHC为
 (7)
(7)
式中,残余重力异常的垂直梯度按照式(8)计算[18]
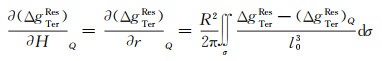 (8)
(8)
式中,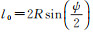
与地面重力测量不同,航空重力测量采用差分GPS动态定位测定空中测线采样点的大地坐标,获取的重力观测值为重力扰动。式(3)中航空重力数据贡献的残余高程异常ζAirRes可利用带谱权的广义Hotine积分由残余航空重力扰动计算
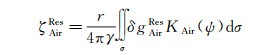 (9)
(9)
式中,KAir(ψ)为带谱权的广义Hotine核函数,写为
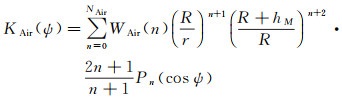 (10)
(10)
式中,hM为平均飞行高度(大地高);NAir为航空重力数据对应的最大展开阶数;WAir(n)为第n阶航空重力谱权。
式(9)中的残余航空重力扰动δgAirRes按照式(11)计算
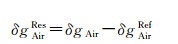 (11)
(11)
式中,δgAir为平均高度面的航空重力扰动,航空重力数据采集时飞机的实际飞行高度与平均飞行高度一般控制在±50m以内,可采用一阶Taylor级数展开将采样点处的重力扰动精确归算至平均高度面。δgAirRef为由参考重力场模型计算的参考航空重力扰动。
利用由高分辨率DEM计算的重力高频地形效应,结合地面重力谱权,式(3)中的RTM高程异常ζTerRTM为
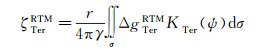 (12)
(12)
谱组合方法的关键在于合理确定各类重力数据的相对谱权,这需要各类重力数据的误差信息。地面和航空重力数据互为独立观测,误差阶协方差可设为零,在确定谱权时只需要考虑各自的误差阶方差信息[14-15]。地面重力数据的谱权WTer(n)和航空重力数据的谱权WAir(n)按照式(13)—式(15)计算
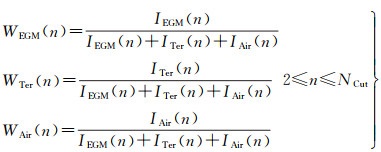 (13)
(13)
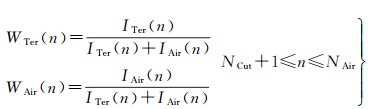 (14)
(14)
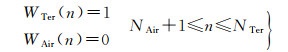 (15)
(15)
式中,IEGM(n)、ITer(n)和IAir(n)分别为参考重力场模型、地面和航空重力数据的误差阶方差的倒数
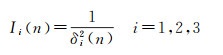 (16)
(16)
式中,δi2(n)为各类数据的误差阶方差。
由式(13)—式(16)可知,谱权确定问题转化为各类重力数据的误差阶方差估计问题。本文采用一种直接从测量数据本身出发估计其误差和误差阶方差的方法,可称为数据驱动法,其基本思想是:在低阶部分(如NCut=200阶以下),以参考重力场模型作为基准,将地面和航空重力数据与参考重力场模型进行对比,利用球谐分析进行谱分解估计地面和航空重力数据的长波误差及低阶误差阶方差;在中、高阶部分(如NCut=200阶以上),使用舍一交叉验证方法(leave-out-one cross validation, LOOCV),直接由地面和航空重力数据本身估计其中、短波误差和中、高阶误差阶方差。数据驱动法的优势在于不需要重力数据的先验误差信息,获取的误差阶方差和谱权与实际重力数据达到最佳符合。关于数据驱动的误差阶方差估计方法,详细论述见文献[6]。
1.2 高程异常—大地水准面差距转换改正项因珠峰地区属于特大山区,地形和重力场起伏大,应采用顾及地形质量影响的严密公式(式(17))计算高程异常—大地水准面差距转换改正项[19]
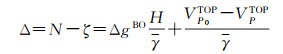 (17)
(17)
式中,N为大地水准面差距;ζ为高程异常;γ为椭球面点至似地形表面点之间的平均正常重力;VPTOP为地形质量在待求点产生的引力位;VP0TOP为地形质量在大地水准面上投影点产生的引力位。ΔgBO为精细布格重力异常,计算公式为
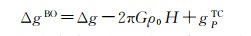 (18)
(18)
式中,Δg为珠峰峰顶的重力异常;H为地形高度;G为万有引力常数;ρ0为平均地壳密度;gPTC为地形改正。以上计算需要用到珠峰峰顶的重力值和珠峰区域高分辨率DEM数据。
1.3 基于国际高程参考系统的大地水准面差距零阶项大地水准面差距零阶项N0的计算涉及高程基准的定义和选取。我国高程以1985国家高程基准(黄海多年平均海平面)作为高程起算面,尼泊尔法定高程则从印度洋孟加拉湾平均海平面起算。为确定中尼均认可的珠峰高程基准,双方决定:根据国际大地测量协会2015年发布的关于国际高程参考系统定义和实现的官方决议[1],采用国际高程参考系统定义的重力位值W0[20-21]和GRS80参考椭球[22],确定基于国际高程参考系统的珠峰峰顶大地水准面差距,作为国际高程参考系统中珠峰正高的起算基准。因此,大地水准面差距零阶项N0的计算公式为[18, 23]
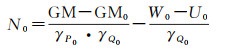 (19)
(19)
式中,GM=3.986004415×1014m3s-2,为地心引力常数;GM0=3.986005×1014m3s-2,为GRS80椭球的地心引力常数;W0=62636853.4m2s-2,为国际高程参考系统定义的重力位值;U0=62636860.850m2s-2,为GRS80椭球的正常重力位值;r为大地水准面上相应点的地心距离;γ为椭球面上相应点的正常重力值。
2 数据处理与分析 2.1 珠峰区域和数据情况建立珠峰地区的高精度大地水准面模型是精确测定珠峰高程的关键所在,这需要密集、均匀分布的高精度重力数据。在珠峰及周边区域(25°N—32°N、83°E—91°E)已有8022点历史地面重力数据,但点位分布很不均匀,特别是在珠峰及邻近区域地面重力点十分稀少。2020年5月1日—2020年6月11日期间,在珠峰地区成功开展航空重力测量,有效解决了该区域的重力数据稀少/空白问题。
航空重力测量使用航空地质一号(空中国王350ER型飞机),从拉萨贡嘎机场起降,地面架设3个GNSS基准站,同机搭载GT-2A型航空重力仪和DGA-01型国产航空重力仪,平均飞行速度441.7km/h,平均飞行高度10249m(大地高),共采集了东西向数据测线39条,南北向检验测线9条,形成264个交叉点,测线间距5km,在珠峰邻近区域数据测线间距加密为2.5km,测线总长度5635.2km,覆盖面积1.27万km2,数据采样率2Hz,共获取83803个数据点。选取同架次、同测线观测数据进行比较,GT-2A型和DGA-01型航空重力仪的内符合精度达0.34mGal,具有良好的一致性,最终采用GT-2A型航空重力仪的数据。航空重力数据处理采用GT-2A随机软件,经100s卡尔曼测线滤波处理和交叉点平差(调平)后,测线网交叉点差值RMS为1.1mGal。利用GNSS差分动态定位测定空中数据点的大地坐标,测线观测值为重力扰动。利用CG-5型相对重力仪,采用往返重复观测方式与国家重力基本点联测,获取飞机停机坪上航空重力仪正下方点位的绝对重力值,测量精度±7μGal。珠峰地区航空重力测线网如图 1所示,其中黑色线表示航空重力测线,红色点表示GNSS水准点,紫色矩形框表示似大地水准面模型范围,底图采用SRTM地形数据绘制。

|
| 注:蓝色三角形代表珠峰。 图 1 珠峰地区航空重力测线网与GNSS水准并置点 Fig. 1 Airborne gravity survey lines and GNSS leveling points in the region of Mount Qomolangma |
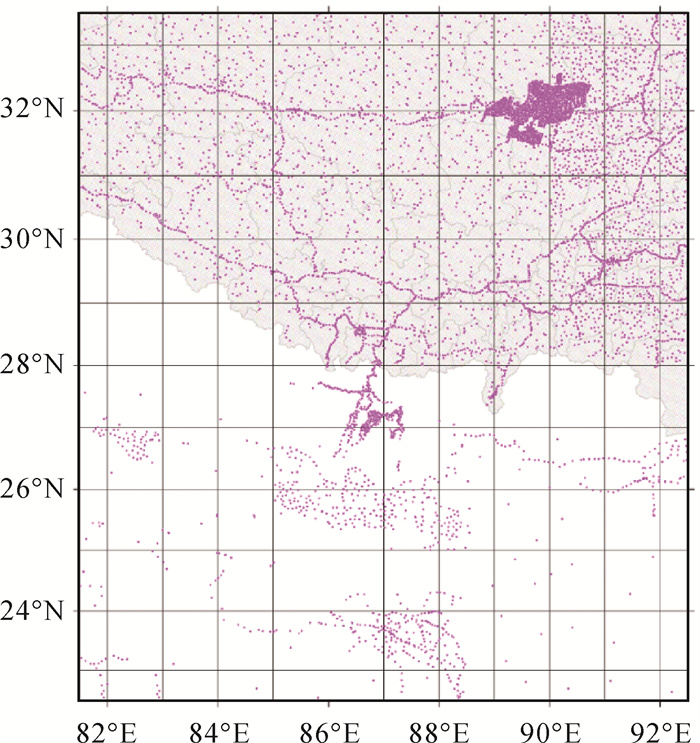
利用国产Z400型相对重力仪,在世界上首次获取了珠峰峰顶重力观测值。2005年珠峰高程测量时重力测量推进到海拔高度7790m,通过推算得到峰顶重力值[24-26]。此次获取的峰顶实测重力值,有助于提升高程异常—大地水准面差距转换改正项的计算精度[19]。此外,在珠峰邻近区域拓展了4条新路线,结合水准路线和登山路线,使用CG-6型相对重力仪共新测了210点地面重力数据,重力值精度优于±39.5μGal,结合该区域已有8022点地面重力数据,共有8232点地面重力数据可供使用。所有地面重力数据均统一到2000国家重力基本网,在进行粗差剔除时,没有发现粗差点。珠峰及周边区域地面重力数据空间分布如图 2所示。
|
| 图 2 珠峰及周边区域地面重力数据 Fig. 2 Terrestrial gravity data in the region of Mount Qomolangma |
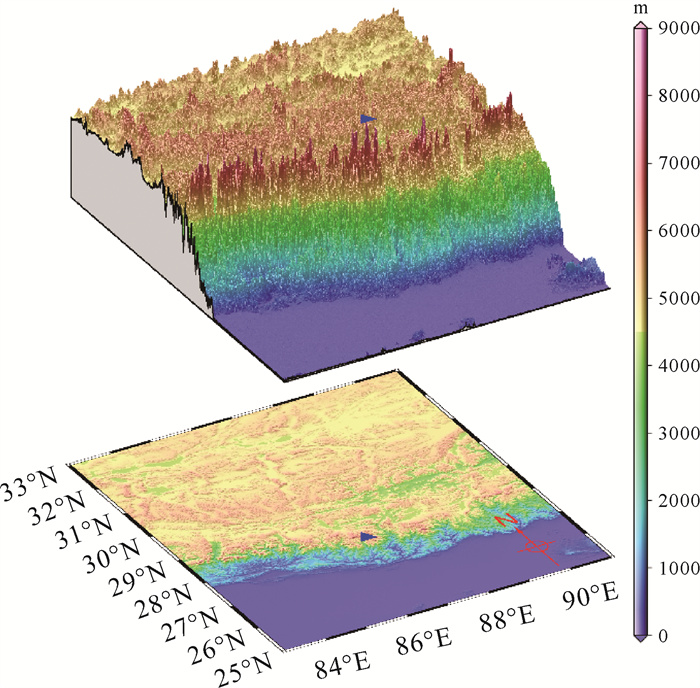
高分辨率DEM数据采用3″×3″ SRTM数据[27],覆盖范围为25°N—32°N、83°E—91°E,基于SRTM数据的珠峰及周边区域地形起伏如图 3所示。
|
| 注:蓝色三角形代表珠峰。 图 3 珠峰及周边区域SRTM地形起伏 Fig. 3 SRTM topography in the region of Mount Qomolangma |
设立由61个点组成的珠峰局部GNSS控制网,每点开展GNSS观测1~2个时段,时段长度约8~14h,各点大地高的平均精度为3.5mm。这61个点是GNSS水准并置点,结合水准测量获取各点的正常高,相对于起算点(国家一等水准点“日喀则基岩点北”)的高程中误差为0.1~1.84mm,由此得到61个GNSS水准点的高程异常,用于珠峰地区重力似大地水准面模型精度检核。61个GNSS水准并置点空间分布如图 1所示。
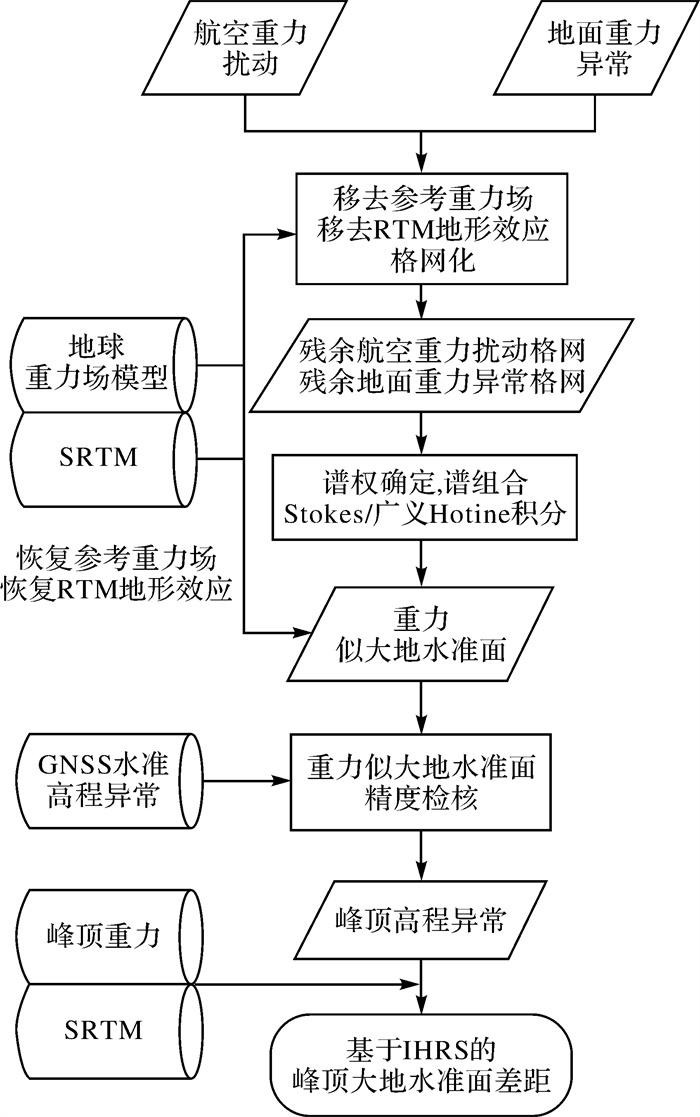
2.2 计算方案利用谱组合方法联合航空重力扰动和地面重力异常数据计算珠峰地区重力似大地水准面,进而确定基于国际高程参考系统的峰顶大地水准面差距,计算方案如图 4所示。重力似大地水准面模型覆盖范围为27.75°N—28.9°N、86.4°E—87.7°E,空间分辨率1′×1′。计算中采用Molodensky解析延拓法及基于地球重力场模型和RTM的移去-计算-恢复技术。对比分析地球重力场模型EGM2008[28]、EIGEN6-C4[29]和XGM2019[30],优选合适的参考重力场模型及其截断阶数。利用3″×3″ SRTM数据计算地面重力异常高频地形效应。重力数据格网化采用反距离加权插值方法,分别得到1′×1′残余航空重力扰动格网和2′×2′残余地面重力异常格网。以61个GNSS水准并置点的高程异常为基准值,对重力似大地水准面模型进行精度测试分析,优选合适的Stokes和Hotine积分球冠半径。利用珠峰地区重力似大地水准面模型,顾及高差改正内插计算得到峰顶高程异常,根据严密公式(式(17))施加高程异常—大地水准面差距转换改正,结合基于国际高程参考系统的大地水准面零阶项(式(19)),最终确定基于国际高程参考系统的珠峰峰顶大地水准面差距。
|
| 图 4 珠峰地区重力似大地水准面和峰顶大地水准面差距计算方案 Fig. 4 Computation scheme for gravimetric quasigeoid in the region of Mount Qomolangma and geoid undulation at the summit |
2.3 航空和地面重力数据的谱权确定
由式(5)和式(10)可知,在谱组合中引入各类重力数据的谱权,实质上是按照阶数对Stokes、Hotine积分核函数进行修改,实现对航空和地面重力数据对应高程异常贡献的调节,以获得最优的似大地水准面结果。根据式(13)—式(16),谱权确定有赖于各类重力数据误差阶方差的准确估计,采用基于数据驱动的误差和误差阶方差估计方法[6],在低阶部分(2~200阶),以参考重力场模型(2~200阶)作为基准,分别将航空重力扰动、地面重力异常与参考重力场模型值作差得到残余航空重力扰动和残余地面重力异常,并插值形成格网。在珠峰区域以外的格网点,采用参考重力场模型值(≥201阶)填充,形成全球范围的残余空中重力扰动格网和残余地面重力异常格网,进行球谐分析得到表征重力数据长波误差的200阶球谐系数,再分别计算得到航空和地面重力数据在2~200阶的误差阶方差。在中、高阶部分(≥201阶),采用LOOCV方法,欲估计某点的重力误差,先舍弃该待求点,利用该点周围多个点的重力观测值内插得到待求点的重力内插值,将内插值与观测值之差作为重力数据的中、短波误差估值。分别获得所有航空和地面重力数据点的误差估值后,插值形成5′×5′的误差格网,由误差格网推算误差协方差函数,进而分别计算出航空和地面重力数据在201~2160阶的误差阶方差。至此,笔者获取了航空和地面重力数据在2~2160阶的误差阶方差,即可按照式(13)—式(16)确定相应的谱权。
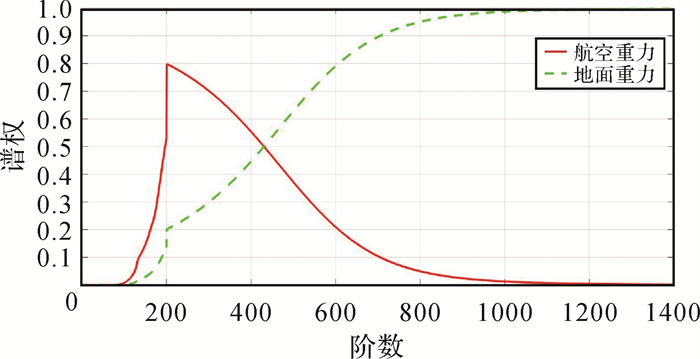
图 5为珠峰区域航空和地面重力数据的谱权。由图 5可以看出,航空重力数据的贡献谱段集中在140~700阶之间,航空重力谱权大约从120阶开始快速上升,在200阶左右达到顶点,最大谱权达0.8,随后逐渐下降。200阶以上航空和地面重力谱权之和为1,两者是此降彼升的关系,航空重力数据的贡献越小,地面重力数据的贡献则越大,1000阶以上航空重力数据的贡献基本可忽略不计,谱组合主要是来自地面重力数据的贡献。
|
| 图 5 航空与地面重力数据的谱权 Fig. 5 Spectral weights of airborne and terrestrial gravity data |
2.4 参考重力场模型和球冠积分半径的测试分析
由于航空和地面重力数据覆盖范围有限,需利用参考重力场模型作为区域以外重力场信息的贡献,具体实现采用移去-计算-恢复技术。选取不同的地球重力场模型作为参考场、同一个模型选取不同的截断阶数,会得出不同的重力似大地水准面结果,有必要对不同参考重力场模型和模型截断阶数进行测试分析。选择地球重力场模型EGM2008、EIGEN6-C4和XGM2019作为参考重力场的备选,3个模型均展开至2190阶,利用珠峰地区61点GNSS水准高程异常数据对模型进行精度评价。表 1列出了由3个重力场模型计算的高程异常与61点GNSS水准高程异常之间的差值统计信息。由表 1可以看出,在珠峰地区,EIGEN-6C4模型精度最高,XGM2019模型次之,EGM2008模型最差。EIGEN-6C4模型和XGM2019模型分别由不同机构研制,采用的数据和方法不尽相同,两者最大的区别是XGM2019模型利用DEM正演建模技术推算高频重力异常(719阶以上)[30],这可能是XGM2019模型精度稍低于EIGEN-6C4模型的原因。因此,选定EIGEN-6C4模型作为重力似大地水准面计算的参考重力场模型。
| 地球重力场模型 | 最小值 | 最大值 | 平均值 | 标准差 |
| EGM2008 | -0.757 | 0.633 | 0.111 | 0.279 |
| EIGEN-6C4 | 0.095 | 0.625 | 0.434 | 0.126 |
| XGM2019 | -0.228 | 0.691 | 0.319 | 0.162 |
再测试参考重力场模型的截断阶数,表 2为EIGEN-6C4模型截取至不同阶数时、联合航空和地面重力数据解算的重力似大地水准面与61点GNSS水准高程异常的差值统计信息。结果表明,参考重力场模型EIGEN-6C4截取至1080阶时的结果是最优的,精度达3.8cm。若截取阶数偏高,会削弱区域内实测重力数据的贡献,导致重力似大地水准面难以达到最佳精度。若截取阶数偏低,区域外重力场截断误差增大,导致结果精度偏低。
| EIGEN-6C4模型截断阶数 | 最小值 | 最大值 | 平均值 | 标准差 |
| 2190 | 0.086 | 0.369 | 0.284 | 0.044 |
| 1080 | 0.148 | 0.333 | 0.270 | 0.038 |
| 720 | 0.284 | 0.481 | 0.370 | 0.045 |
| 360 | 0.175 | 0.394 | 0.291 | 0.047 |
根据式(4)和式(9)可知,优选合适的Stokes和Hotine积分球冠半径,对获取最佳的重力似大地水准面模型也是至关重要的。表 3为选取不同球冠积分半径时、联合航空和地面重力数据解算的重力似大地水准面与61点GNSS水准高程异常的差值统计信息。结果显示,当球冠积分半径取1°,重力似大地水准面模型精度最高。
| 球冠积分半径/(°) | 最小值 | 最大值 | 平均值 | 标准差 |
| 0.50 | 0.041 | 0.301 | 0.209 | 0.064 |
| 0.75 | 0.095 | 0.326 | 0.242 | 0.048 |
| 1.00 | 0.148 | 0.333 | 0.270 | 0.038 |
| 1.25 | 0.135 | 0.344 | 0.281 | 0.039 |
| 1.50 | 0.128 | 0.333 | 0.272 | 0.039 |
| 2.00 | 0.107 | 0.312 | 0.250 | 0.040 |
2.5 重力似大地水准面模型精度评估
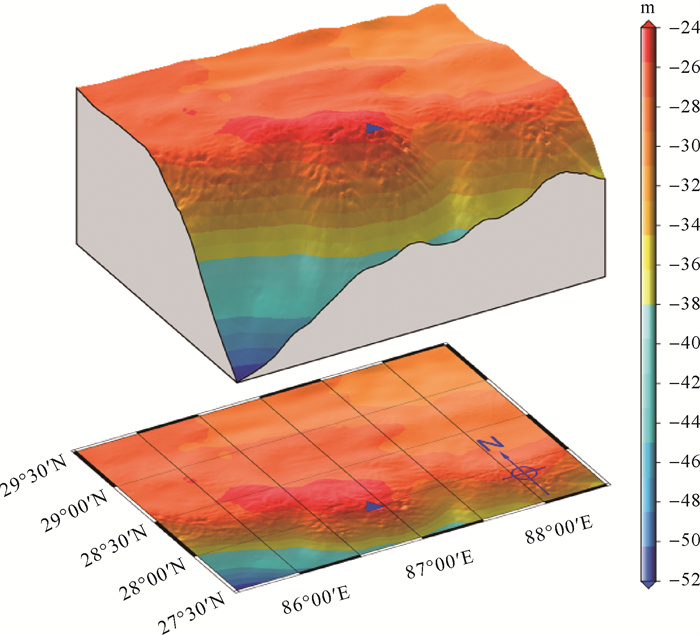
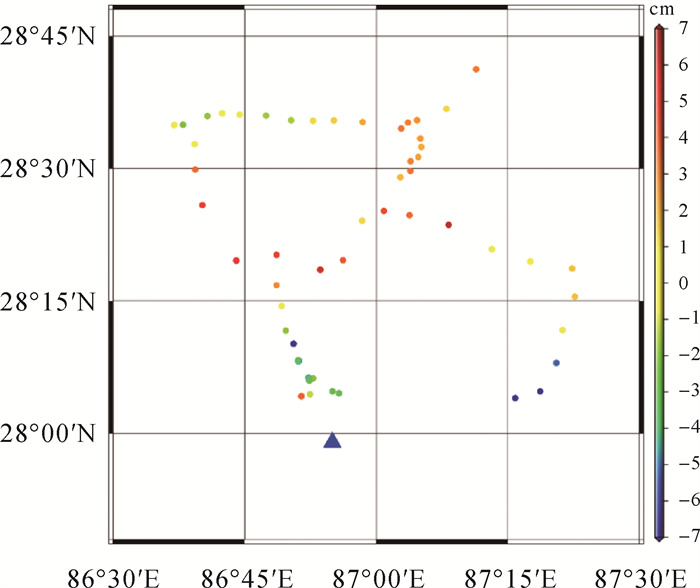
根据以上重力似大地水准面模型与GNSS水准高程异常的比较分析结果,选定参考重力场模型为EIGEN-6C4,并截取至1080阶,Stokes和Hotine积分球冠半径选定为1°。利用谱组合方法联合航空和地面重力数据解算得到重力似大地水准面模型(图 6),经61点GNSS水准高程异常检核,模型精度达到3.8cm。图 7为该模型与61点GNSS水准高程异常的差值(已扣除平均值)。
|
| 注:蓝色三角形代表珠峰。 图 6 联合航空和地面重力数据构建的重力似大地水准面模型 Fig. 6 Gravimetric quasigeoid model computed from the combination of airborne and terrestrial gravity data |
|
| 注:蓝色三角形代表珠峰。 图 7 重力似大地水准面模型与GNSS水准高程异常的差值 Fig. 7 Differences between gravimetric quasigeoid model and GNSS leveling measured height anomalies |
将谱组合方法称为方案1,本文还采用了另外两种计算方案进行对比分析。方案2是利用EIGEN-6C4模型和地面重力异常数据,不使用航空重力数据,采用基于移去-计算-恢复的Molodensky方法计算重力似大地水准面[18, 26]。在Molodensky级数解公式中以地形改正项代替Molodensky级数解重力一阶改正项。利用移去-恢复技术由均衡重力异常计算得到格网平均重力异常,均衡改正计算选择爱黎-海斯卡宁模型,均衡深度选34km。
方案3是利用基于快速傅里叶变换(FFT)的泊松积分法将航空重力异常数据向下延拓至地面,与地面重力异常数据融合形成格网平均重力异常后,结合EIGEN-6C4模型,采用基于移去-计算-恢复的Molodensky方法计算重力似大地水准面。
利用珠峰地区61点GNSS水准高程异常数据对重力似大地水准面模型进行精度评估,基于3种方案的重力似大地水准面模型相对于GNSS水准高程异常的差值统计信息见表 4。结果表明,与单独利用地面重力数据相比,加入航空重力数据能够显著提高重力似大地水准面模型的精度,方案1和方案3的提升幅度分别为51.3%和38.5%。方案1的结果要优于方案3,这主要归功于谱组合方法不需要对航空重力数据进行显式的向下延拓处理,而是一步联合航空和地面重力数据计算似大地水准面。方案3则是两步法,需要将航空重力数据向下延拓、再与地面重力数据融合后进行积分计算,航空重力数据的利用率显然低于方案1。
| 计算方案 | 最小值 | 最大值 | 平均值 | 标准差 |
| 方案1(航空+地面) | 0.148 | 0.333 | 0.270 | 0.038 |
| 方案2(地面) | -0.129 | 0.270 | 0.169 | 0.078 |
| 方案3(航空+地面) | 0.166 | 0.371 | 0.314 | 0.048 |
表 4中的平均差值代表珠峰区域重力似大地水准面(不含零阶项)与我国1985国家高程基准的垂直偏差。根据笔者和相关学者的研究结果,重力似大地水准面(不含零阶项)与1985国家高程基准之间的垂直偏差介于28~35cm[31-34]。加入航空重力数据后,平均差值分别从16.9cm增大为27cm(方案1)和31.4cm(方案3),体现了航空重力数据对重力似大地水准面的贡献,使之更为接近真实值。
2.6 基于国际高程参考系统的峰顶大地水准面差距确定 2.6.1 顾及高差改正的峰顶高程异常插值计算珠峰峰顶高程异常可由重力似大地水准面模型经样条插值或双线性插值得到。珠峰地区地形起伏剧烈,由模型内插计算峰顶高程异常不同于其他地区,应考虑高程变化对内插高程异常的影响,并进行相应的高差改正。
似大地水准面模型的格网计算点是由计算者选定、用于表示地表的特定DEM确定。设在似大地水准面模型计算时用1′×1′ DEM代表地表格网计算点,若某地面点P的高程为h,由1′×1′ DEM内插得到该点在DEM面上对应点P0的高程为h0,由对应的1′×1′似大地水准面模型内插得到点P在DEM面上对应点P0的高程异常为ζ0,则P点的实际高程异常ζ为
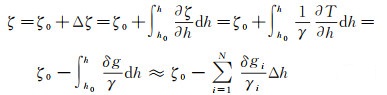 (20)
(20)
计算式(20)时,将点P0至点P的高差分为N=100个等分高差段Δh,δgi和γi为每个高差段中点Pi的重力扰动和正常重力,δgi由式(21)计算
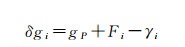 (21)
(21)
式中,gP为点P的重力值;Fi为点P沿垂线到点Pi的空间改正。
珠峰地区重力似大地水准面计算时采用1′×1′ DEM作为地表计算点格网。利用峰顶点实际正高及其在1′×1′ DEM地形面上投影点的正高,结合峰顶实测重力值,根据式(21)计算得到峰顶内插高程异常的高差改正Δζ=-0.05m。
为检核高差改正计算的正确性,根据珠峰峰顶精确三维坐标,利用谱组合方法联合航空和地面重力数据,直接单点积分计算得到峰顶高程异常。对比峰顶高程异常的单点积分结果与顾及高差改正的模型内插结果,两者仅相差0.9cm,这证明了高差改正的必要性和正确性。
2.6.2 基于国际高程参考系统的峰顶大地水准面差距计算利用方案1构建的重力似大地水准面模型,经样条插值和高差改正得到峰顶高程异常ζ。根据式(17)和式(18),利用珠峰峰顶实测重力值和3″×3″ SRTM数据计算得到峰顶高程异常转换为大地水准面差距的改正项Δ=-1.302m。根据式(19),采用国际高程参考系统定义的重力位值,选定GRS80参考椭球,计算得到大地水准面差距零阶项N0=-0.177m,最终按照式(1)计算得到基于国际高程参考系统的峰顶大地水准面差距。采用基于方案3的重力似大地水准面模型计算得到峰顶大地水准面差距,与方案1所得峰顶大地水准面差距结果仅相差3.6cm。
3 结论2020珠峰高程测量,成功获取珠峰峰顶及周边区域1.27万km2的航空重力数据,测线网平均精度达1.1mGal,有效填补了珠峰地区重力数据空白。联合航空和地面重力数据,建立了珠峰区域1′×1′高精度重力似大地水准面模型,基于国际高程参考系统定义的重力位值W0和GRS80参考椭球,确定了国际高程参考系统中的珠峰峰顶大地水准面差距,为中国和尼泊尔合作确定基于国际高程参考系统的珠峰正高提供了高精度基准。
基于谱组合理论和数据驱动的谱权确定方法,联合航空和地面重力数据解算的重力似大地水准面模型,经61个GNSS水准并置点的高程异常检核,模型精度达3.8cm。加入航空重力数据能有效填充地面重力数据空白,谱组合中航空重力数据的贡献谱段集中在140~700阶。与单独利用地面重力数据相比,航空重力数据使得重力似大地水准面模型精度提升了51.3%(3.8cm VS 7.8cm)。
珠峰地区地形极端崎岖、重力场变化剧烈,利用重力似大地水准面模型计算珠峰峰顶大地水准面差距时,有必要采用顾及高差改正的内插方法和顾及地形质量影响的高程异常—大地水准面差距转换改正公式,结合此次采集的峰顶地面重力数据,以确保峰顶大地水准面差距的计算精度。
国际大地测量协会2015年发布了国际高程参考系统的定义,并于2019年提出了建立国际高程参考框架(IHRF)的远景目标[35]。2020珠峰高程测量成功在珠峰地区实现了国际高程参考系统,可为建立国际高程参考框架提供重要参考。现阶段,我国及全球范围仍存在较大范围地面重力数据空白区域,已有重力数据的精度和现势性也亟须提升、更新。开展大规模航空重力测量,获取均匀分布的高精度重力数据,进一步发展多种类型重力数据融合处理的理论和方法,对于厘米级精度重力大地水准面模型构建和全球高程基准统一具有重要价值。
致谢: 特此向为2020珠峰高程测量作出贡献的专家学者、测绘队员和登山队员表示衷心的感谢。
| [1] |
INTERNATIONAL ASSOCIATION OF GEODESY. IAG resolutions adopted by the IAG council at the XXVIth IUGG general assembly[EB/OL]. [2015-6-22]. https://office.iag-aig.org/iag-and-iugg-resolutions.
|
| [2] |
WANG Y M, SALEH J, ROMAN D. The US gravimetric geoid of 2009 (USGG2009): model development and evaluation[J]. Journal of Geodesy, 2012, 86(3): 165-180. DOI:10.1007/s00190-011-0506-7 |
| [3] |
李建成. 最新中国陆地数字高程基准模型: 重力似大地水准面CNGG2011[J]. 测绘学报, 2012, 41(5): 651-660. LI Jiancheng. The recent Chinese terrestrial digital height datum model: gravimetric quasi-geoid CNGG2011[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 651-660. |
| [4] |
SMITH D A, HOLMES S A, LI X P, et al. Confirming regional 1cm differential geoid accuracy from airborne gravimetry: the geoid slope validation survey of 2011[J]. Journal of Geodesy, 2013, 87(10-12): 885-907. DOI:10.1007/s00190-013-0653-0 |
| [5] |
JEKELI C, YANG H J, KWON J H. Geoid determination in South Korea from a combination of terrestrial and airborne gravity anomaly data[J]. Journal of the Korean Society of Surveying, Geodesy, Photogrammetry and Cartography, 2013, 31(6-2): 567-576. |
| [6] |
JIANG T, WANG Y M. On the spectral combination of satellite gravity model, terrestrial and airborne gravity data for local gravimetric geoid computation[J]. Journal of Geodesy, 2016, 90(12): 1405-1418. DOI:10.1007/s00190-016-0932-7 |
| [7] |
WANG Y M, BECKER C, MADER G, et al. The geoid slope validation survey 2014 and GRAV-D airborne gravity enhanced geoid comparison results in Iowa[J]. Journal of Geodesy, 2017, 91(10): 1261-1276. DOI:10.1007/s00190-017-1022-1 |
| [8] |
ZHANG C Y, DANG Y M, JIANG T, et al. Heterogeneous gravity data fusion and gravimetric quasigeoid computation in the coastal area of China[J]. Marine Geodesy, 2017, 40(2-3): 142-159. DOI:10.1080/01490419.2017.1282899 |
| [9] |
NOVÁK P, HECK B. Downward continuation and geoid determination based on band-limited airborne gravity data[J]. Journal of Geodesy, 2002, 76(5): 269-278. DOI:10.1007/s00190-002-0252-y |
| [10] |
HWANG C, HSIAO Y S, SHIH H C, et al. Geodetic and geophysical results from a Taiwan airborne gravity survey: data reduction and accuracy assessment[J]. Journal of Geophysical Research Solid Earth, 2007, 112: B04407. |
| [11] |
FORSBERG R, SAHRUM S, ALSHAMSI A, et al. Coastal geoid improvement using airborne gravimetric data in the United Arab Emirates[J]. International Journal of Physical Sciences, 2012, 7(45): 6012-6023. |
| [12] |
孙中苗, 翟振和, 肖云. 渤海湾航空重力及其在海域大地水准面精化中的应用[J]. 测绘学报, 2014, 43(11): 1101-1108. SUN Zhongmiao, ZHAI Zhenhe, XIAO Yun. Airborne gravimetry in Bohai bay and its role on the refining of the regional marine geoid[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(11): 1101-1108. |
| [13] |
TSCHERNING C C, RAPP R H. Closed covariance expressions for gravity anomalies, geoid undulations, and deflections of the vertical implied by anomaly degree variance models[R]. Columbus, Ohio: Ohio State University, 1974.
|
| [14] |
WENZEL H G. Geoid computation by least-squares spectral combination using intergral kernels[C]//Proceedings of 1982 General IAG Meeting. Tokyo, Japan: [s. n. ], 1982: 438-453.
|
| [15] |
SJOBERG L. Least squares combination of satellite and terrestrial data in physical geodesy[J]. Annales Geophysicae, 1981, 37(1): 25-30. |
| [16] |
DENKER H, BARRIOT J P, BARZAGHI R, et al. The development of the European gravimetric geoid model EGG07[C]//Proceedings of 2009 Observing Our Changing Earth. Berlin, Germany: Springer, 2009: 177-185.
|
| [17] |
FORSBERG R. A study of terrain reductions, density anomalies and geophysical inversion methods in gravity field modelling[R]. Columbus, Ohio: Ohio State University, 1984.
|
| [18] |
HOFMANN W B, MORITZ H. Physical geodesy[M]. Austria: Springer, 2005.
|
| [19] |
FLURY J, RUMMEL R. On the geoid-quasigeoid separation in mountain areas[J]. Journal of Geodesy, 2009, 83: 829-847. DOI:10.1007/s00190-009-0302-9 |
| [20] |
IHDE J, SANCHEZ L, BARZAGHI R, et al. Definition and proposed realization of the international height reference system (IHRS)[J]. Surveys in Geophysics, 2017, 38(3): 549-570. DOI:10.1007/s10712-017-9409-3 |
| [21] |
SANCHEZ L, SIDERIS M G. Vertical datum unification for the international height reference system (IHRS)[J]. Geophysical Journal International, 2017, 209(2): 570-586. |
| [22] |
MORITZ H. Geodetic reference system 1980[J]. Journal of Geodesy, 2000, 74: 128-133. DOI:10.1007/s001900050278 |
| [23] |
SANCHEZ L, GREN J, HUANG J L, et al. Strategy for the realisation of the international height reference system (IHRS)[J/OL]. [2021-11-15]. https://doi.org/10.1007/s00190-021-01481-0
|
| [24] |
陈俊勇, 张燕平, 岳建利, 等. 2005珠峰高程测定[J]. 测绘学报, 2006, 35(1): 1-3. CHEN Junyong, ZHANG Yanping, YUE Jianli, et al. 2005 height determination of Qomolangma Feng[J]. Acta Geodaetica et Cartographica, 2006, 35(1): 1-3. DOI:10.3321/j.issn:1001-1595.2006.01.001 |
| [25] |
陈俊勇, 岳建利, 郭春喜, 等. 2005珠峰高程测定的技术进展[J]. 中国科学(D辑, 地球科学), 2006, 36(3): 280-286. CHEN Junyong, YUE Jianli, GUO Chunxi, et al. Technical progress of 2005 height determination of Qomolangma peak[J]. Science in China Series D: Earth Science, 2006, 36(3): 280-286. |
| [26] |
郭春喜, 宁津生, 陈俊勇, 等. 珠峰地区似大地水准面精化与珠峰顶正高的确定[J]. 地球物理学报, 2008, 51(1): 101-107. GUO Chunxi, NING Jinsheng, CHEN Junyong, et al. Improvement of regional quasi-geoid in Qomolangma (Mt. Everest) and determination of orthometric elevation[J]. Chinese Journal of Geophysics, 2008, 51(1): 101-107. |
| [27] |
FARR T G, ROSEN P, CARO E, et al. The shuttle radar topography mission[J]. Reviews of Geophysics, 2007, 45(2): RG2004. DOI:10.1029/2005RG000183 |
| [28] |
PAVLIS N K, HOLMES S A, KENYON S, et al. The development and evaluation of the Earth gravitational model 2008 (EGM2008)[J]. Journal of Geophysical Research Solid Earth, 2012, 117: B04406. |
| [29] |
FÖRSTE C, BRUINSMA S, FLECHTNER, et al. A new release of EIGEN-6C[C]//Proceedings of 2012 AGU Fall Meeting. San Francisco, U.S. : [s. n. ], 2012.
|
| [30] |
ZINGERLE P, PAIL R, GRUBER T, et al. The combined global gravity field model XGM2019e[J]. Journal of Geodesy, 2020, 94(7): 419-432. |
| [31] |
郭海荣, 焦文海, 杨元喜. 1985国家高程基准与全球似大地水准面之间的系统差及其分布规律[J]. 测绘学报, 2004, 33(2): 100-104. GUO Hairong, JIAO Wenhai, YANG Yuanxi. The systematic difference and its distribution between the 1985 national height datum and the global quasigeoid[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(2): 100-104. |
| [32] |
翟振和, 魏子卿, 吴富梅, 等. 利用EGM2008位模型计算中国高程基准与大地水准面间的垂直偏差[J]. 大地测量与地球动力学, 2011, 31(4): 116-118. ZHAI Zhenhe, WEI Ziqing, WU Fumei, et al. Computation of vertical deviation of Chinese height datum from geoid by using EGM2008 model[J]. Journal of Geodesy and Geodynamics, 2011, 31(4): 116-118. |
| [33] |
许厚泽. 全球高程系统的统一问题[J]. 测绘学报, 2017, 46(8): 939-944. XU Houze. Global unification problem of the height system[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(8): 939-944. DOI:10.11947/j.AGCS.2017.20170406 |
| [34] |
赫林, 李建成, 褚永海. 1985国家高程基准与全球高程基准之间的垂直偏差[J]. 测绘学报, 2016, 45(7): 768-774. HE Lin, LI Jiancheng, CHU Yonghai. The vertical shift between 1985 national height datum and global vertical datum[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(7): 768-774. DOI:10.119471/j.AGCS.2016.20160029 |
| [35] |
International Association of Geodesy. IAG resolutions adopted by the IAG council at the XXVⅡth IUGG general assembly[EB/OL]. [2019-07-08]. https://office.iag-aig.org/iag-and-iugg-resolutions.
|



