北斗导航卫星系统(BeiDou navigation satellite system,BDS)是全球首个全星座播发三频观测数据的卫星导航定位系统,三频数据改善了观测值的冗余度,有利于提升载波相位整周模糊度解算的性能和效率[1-2]。BDS高精度实时动态(real-time kinematic,RTK)定位使用载波相位观测值,定位时通过观测值差分来削弱观测误差的影响,但随着测站距离的增加,与空间相关的观测误差将影响整周模糊度的准确确定[3],载波相位整周模糊度解算方面的研究成果较多,集中在空间相关误差残余下整周模糊度快速、准确固定上[4-6]。空间相关误差中时空变化复杂的电离层延迟误差是影响模糊度固定最主要的因素[7],通常采用无电离层组合消除影响,但使用无电离层组合会带来3个问题:①伪距和相位观测值独立进行电离层参数的消除,两类观测值之间通过电离层延迟误差约束的关系消失;②独立进行无电离层组合时假定两类观测值不是同一个电离层延迟误差参数,理论上不严密;③组合观测值放大了的噪声。同时对于双频以上的观测数据,无电离层组合方式的选择和各组合之间的相关关系等都增加了参数解算的复杂性[8]。非组合方法将每个频率观测信息作为独立观测信号,观测模型统一简单,同时电离层的先验信息和时空约束信息以约束形式引入参数估计中,改进电离层延迟误差的模型化,增强未知参数解算的强度[9-10]。利用非组合观测模型进行参数估计具有许多优势,但是电离层误差无法消除,成为非组合观测模型中需要重点考虑的误差。
利用非组合观测模型进行长基线(测站间距大于100 km)RTK定位时,电离层误差以未知参数的形式进行估计,而随着模型中估计参数的增加,方程的强度变弱,将增加整周模糊度的解算难度[11-12]。利用全球电离层格网地图(global ionospheric map,GIM)、参考站网的NRTK或者PPP-RTK解算的电离层先验信息,可对电离层延迟参数进行先验值约束,加快模糊度收敛速度,先验方差的设置是决定电离层约束效果的关键[13]。电离层权重模型(ionosphere weighted model,IWM)将双差电离层先验值设为零,通过调整先验值的方差进行合理的约束,方差值被表示为与基线长度有关的经验公式或经验值[14-15]。电离层先验值约束需要依赖于外部提供的电离层值,电离层权重模型中先验值的方差确定是其中的关键问题,目前尚无科学确定先验值方差的方法,而电离层在时间和空间上的变化有较好的、可获得的统计特性,对电离层参数时间和空间的合理约束能显著提升模糊度解算的性能[16]。对电离层误差空间相关性的研究主要集中在电离层延迟误差的建模、电离层区域误差改正上,在对附加的电离层参数进行约束时常将电离层描述为与经纬度相关的线性函数,通过估计多项式的系数对电离层误差进行空间约束[17-18]。电离层时间相关性的约束主要采用随机游走过程来表示电离层变化,文献[19]将电离层延迟的随机部分估计为随机游走,通过多个测站的实测电离层延迟的统计分析来建模确定随机游走中的方差。文献[20]对电离层随机部分的变异函数进行相应的更新建模来确定其先验方差。电离层通常会受到短期内不平稳波动的影响,采用经验值和先验方差无法真实有效地反映电离层的变化情况,需要进一步去研究能适应电离层快速变化特性的方差值确定方法。
由于电离层的快速变化和影响因素复杂,建立电离层时间相关性的经验模型十分困难[21]。通过原始载波相位观测值的线性关系可以得到电离层观测值,来反映电离层误差的变化,电离层时间上的变化通常被描述为随机游走,功率谱密度决定了随机游走的过程,因此功率谱密度决定了电离层误差的时变特性,描述了电离层时间上的变化。本文提出一种根据电离层观测值来确定功率谱密度的方法。电离层观测值中包含观测噪声,在差分时间间隔较小时噪声将淹没电离层本身的变化,得到反映电离层时变特性的功率谱密度的关键是电离层观测值中噪声的削弱。本文通过Vondrak平滑方法进行电离层观测值的最佳平滑,使得平滑后的观测值在削弱噪声的同时反映电离层的变化,通过去噪后的电离层观测值计算功率谱密度,不再需要经验公式和先验电离层时间约束值,而是考虑电离层实时特性确定随机游走功率谱密度,是一种简单实用的电离层随机游走方差值确定方法。
1 BDS三频长距离RTK定位方法 1.1 三频观测值RTK定位模型BDS载波相位观测值L(以m为单位)和伪距观测值P在观测时刻t时的站间差分观测方程为
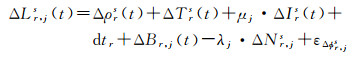 (1)
(1)
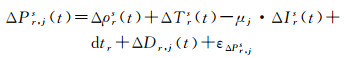 (2)
(2)
式中,Δ表示站间差;r表示接收机;s表示卫星;j为观测值频率;ρ是卫星到接收机的几何距离;T为对流层延迟;I为第一频率的电离层延迟且μj=f12/fj2,fj表示第j个频率;λj=c/fj为载波相位波长;c为光速;dtr是测站间差分后的接收机钟差;Br, j和Dr, j是测站间差分后的相位和伪距的接收机硬件延迟;Nr, js是以周为单位的整周模糊度,吸收了接收机的初始相位偏差;εϕr, js和εPr, js分别为载波相位和伪距的观测噪声。
由式(1)、式(2)可得载波相位观测值和伪距观测值的双差观测方程为
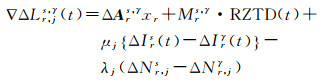 (3)
(3)
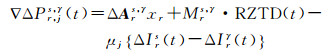 (4)
(4)
式中,∇表示星间差运算符;A为线性化后的用户坐标xr的系数矩阵;M为相对天顶对流层延迟误差RZTD的投影函数。上标γ、s分别表示星间差中的基准卫星及其他卫星,本文选择高度角最高的卫星作为基准卫星,其他符号的含义与式(1)、式(2)相同。式(3)、式(4)的未知参数包含每一颗卫星的电离层延迟误差和整周模糊度参数,未将基准卫星的参数与其他参数合并。这种处理方法避免了星间差分过程中基准卫星变化的问题,数据处理更加简单高效,只需要在后续的解算过程中添加电离层与整周模糊度基准约束即可。电离层延迟误差参数的非差形式,有利于对单颗卫星斜路径的电离层延迟误差进行约束。观测方程的矩阵形式为
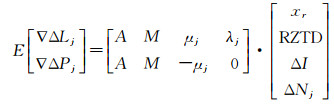 (5)
(5)
式中,E(·)表示期望,本文中观测值的随机模型采用了高度角定权的策略
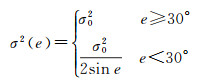 (6)
(6)
式中,σ0为观测值标准差;e为以角度为单位的卫星高度角;σ为卫星信号传播路径方向观测值标准差。文中非差B1、B2、B3载波相位观测值的标准差设为0.003 m,非差P1、P2、P3伪距观测值的标准差设为0.3 m[22]。通过高度角e可得到观测值的先验方差-协方阵。若由原始非差观测值转为双差观测值存在转换矩阵T,则通过该转换矩阵可以得到双差观测值的方差-协方差阵,转换公式为
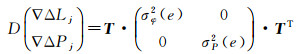 (7)
(7)
式中,D(·)表示方差,通过式(7)得到双差观测值的方差-协方差阵。
1.2 大气参数的时变特性约束方法长基线RTK定位模型中包含了大气延迟未知参数,如何处理每个观测历元都出现的大气延迟参数是关键问题之一。若在每个观测历元独立的估计大气延迟参数,过多的参数将使方程产生秩亏。认为大气延迟参数保持不变的单参数处理法或多参数方法,虽然可以减小未知参数的数量,但忽略了大气短时间的变化[23]。上述大气参数的估计方法显然不是最优的,本文采用随机游走的方式,顾及大气误差的实时变化来对大气参数进行估计。
在对流层延迟误差以投影函数的形式估计之前,可以使用先验对流层模型进行改正[24-25],剩余部分采用随机游走过程进行参数估计。式(5)中对流层延迟参数随机游走过程可以表示为[26]
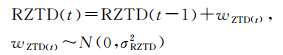 (8)
(8)
式(8)中的随机游走过程描述了两个相邻时刻对流层的变化,变化过程符合均值为0,方差为σRZTD2的正态分布。对流层变化表现较平稳,随机游走的功率谱密度一般取经验值[24-26]。
电离层时间上的变化符合随机游走的特征,可以用随机游走描述其随时间发生的变化,随机游走过程可以表示为[26]
 (9)
(9)
随机游走过程中的方差值σIrs2是影响约束效果的直接因素。方差值与时间间隔及功率谱密度有关,方差与功率谱密度之间的关系为
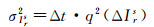 (10)
(10)
式中,q2(Irs)为随机游走中的功率谱密度,描述电离层在Δt时间间隔内的变化量,决定了随机游过的过程,是表征电离层随时间变化快慢的重要指标,对电离层参数时变特性约束的效果在于功率谱密度的选择,为此下文主要对功率谱密度进行研究。
2 利用实测数据计算反映电离层时变特性的功率谱密度 2.1 电离层观测值的功率谱密度计算方法本节从电离层观测值入手研究电离层功率谱密度的计算方法,由式(1)可得含整周模糊度的电离层延迟误差与载波相位观测值的关系
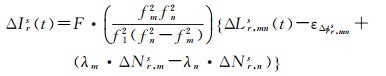 (11)
(11)
式中,ΔLr, mns(t)=ΔLr, ms-ΔLr, ns。通过式(11)得到的电离层包含了真实电离层变化和相位观测值噪声的影响,同时含有相位整周模糊度。式(11)时间差分后电离层为
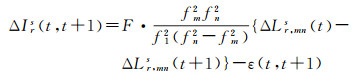 (12)
(12)
ε(t, t+1)表示时间差分后观测值的噪声大小,由式(12)可知,差分后的电离层除含有电离层延迟误差变化外,还包含了观测值的噪声,其中电离层投影函数为
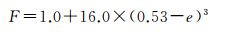 (13)
(13)
式中,F为电离层投影函数;e表示卫星高度角。假设BDS的3个频率载波观测噪声具有相同的标准差,即σε2=σε3=σε1,则式(12)时间差分电离层延迟误差噪声的标准差σε为
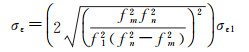 (14)
(14)
式中,σε表示时间差分电离层的噪声标准差,由B1=1 561.098 MHz,B2=1 207.140 MHz,B3=1 268.520 MHz可得,B1、B2组合后历元间差分电离层噪声的标准差相对B1扩大了4.97倍,B1、B3组合后历元间差分电离层噪声的标准差相对B1扩大了5.88倍,B2、B3组合后历元间差分电离层噪声的标准差相对B1扩大了19.18倍。因此通过组合后观测噪声较小的B1、B2观测值得到电离层观测值的变化量,定义时间差分电离层观测值为
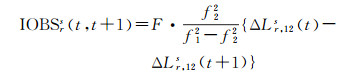 (15)
(15)
式(15)中时间差分电离层观测值包含的观测噪声体现在载波相位观测值上,将式(15)代入式(12)可得
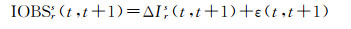 (16)
(16)
由式(16)可以看出,差分电离层观测值中不仅包含电离层的变化,还存在相位观测值噪声的影响。时间差分电离层观测值均值表示一段时间内各个相邻时刻电离层差值变化的整体大小水平,可以表示为
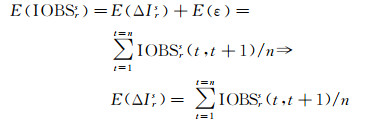 (17)
(17)
式中,n为差分电离层观测值的个数,n=l/Δt,与用于计算均值与方差的数据区间长度l及数据采样间隔Δt有关。时间差分电离层观测值的方差描述了各个相邻时刻电离层差值的变化偏离均值的程度,能够反映电离层的变化特性。当电离层延迟的差分时间间隔很小时,可以假定电离层历元之间变化先验均值为0,通过调整先验值的方差来表示趋近于0的程度[27]。时间差分电离层延迟方差的表达式为
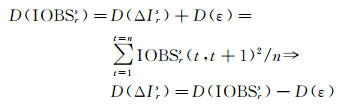 (18)
(18)
若观测值的采样间隔为Δt,则功率谱密度的计算公式为
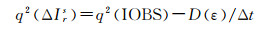 (19)
(19)
式中,q2(IOBSrs)=D(IOBSrs)/Δt表示由电离层观测值直接得到的功率谱密度,包含了观测噪声的影响,由式(19)可以看出,利用电离层观测值求得的功率谱密度受噪声的影响,噪声对功率谱密度影响的大小取决于时间间隔Δt,时间间隔越大,噪声的影响水平越小。但过大的差分间隔会忽略时间间隔内电离层的变化,使电离层的时间分辨率降低,不能反映电离层的快速变化。
2.2 Vondrak平滑确定功率谱密度的方法通过电离层观测值直接得到的功率谱密度受噪声的影响,不能真实反映电离层的变化[28]。利用电离层观测值得到最优功率谱密度的关键是观测值噪声的削弱,移动平滑是最常用的观测值去噪方法,移动平滑中平滑时间的选择非常重要,如果平滑时间较短不能较好地去噪,如果平滑时间过长则会平滑掉电离层本身的变化,平滑时间需要综合考虑对观测值噪声的削弱和电离层的变化的反映[29]。Vondrak滤波可以在观测数据的变化规律和拟合函数未知的情况下,对观测数据进行有效的平滑,因此可以利用Vondrak滤波对观测值噪声进行有效的平滑。Vondrak滤波的基本准则是[30-31]
 (20)
(20)
式中,pi为各观测值的权重;y1, y2, …, yn为观测值序列;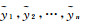
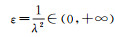
式(20)中,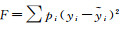
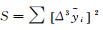
观测误差法确定平滑因子的思想是,从不同平滑因子得到Vondrak滤波平滑后的均方误差中,选择均方误差与已知观测值的观测噪声误差最接近的平滑因子作为最佳平滑因子,可见观测误差法适用于观测噪声已知的情况下。1 s差分间隔的电离层观测值主要是受观测噪声的影响,该值正好反映了电离层观测值中噪声的大小。因已知电离层观测值中噪声的大小水平,本文通过观测误差法来确定平滑因子的大小,由不同平滑因子对观测资料进行Vondrak平滑,得到不同平滑因子对应均方误差(root mean square error,RMSE)[34],RMSE为去噪后的平滑观测值与原始观测值的均方误差,与噪声水平相对应的平滑因子即为最佳平滑因子
 (21)
(21)
选择σ(ε)≈σm的平滑因子作为最后确定的平滑因子,其中σm代表电离层观测值中的噪声。由式(20)可得利用Vondrak平滑电离层观测值最优平滑准则为
 (22)
(22)
式中, pt为不同时刻各观测值的权重;Irs(t)和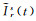
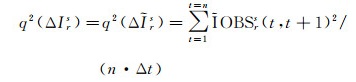 (23)
(23)
式中,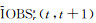
利用长距离实测BDS三频观测数据和广播星历进行算法试验,选取不同经纬度地区的基线,基线长度都超过100 km,数据采样间隔为1 s,试验数据的详细信息见表 1。
| 试验数据 | 基线长度/km | 观测日期 | 测站经纬度 | 采样间隔/s | 时段长度/h |
| Baseline 1 | 110 | 2020-04-28 | 28.13°N, 121.00°E | 1 | 24 |
| Baseline 2 | 120 | 2017-08-06 | 42.44°N, 123.22°E | 1 | 24 |
| Baseline 3 | 160 | 2017-08-06 | 41.18°N, 123.46°E | 1 | 24 |
| Baseline 4 | 200 | 2020-06-10 | 48.30°N, 124.53°E | 1 | 24 |
将4组试验数据分成2 h观测时长的数据段,使用原始伪距和载波相位观测值附加电离层参数时变特性约束的定位模型,把倾斜路径上的电离层延迟误差作为未知参数,根据电离层延迟与伪距和相位及频率的关系统一所有观测值的电离层参数化。相对论效应、潮汐负荷形变(固体潮、极潮和海潮)、萨奈克效应(Sagnac effect)等误差已事先通过模型进行改正。试验中静态模式时位置参数为常数估计,动态时为白噪声估计,先验模型改正后的对流层参数被估计为随机游走参数,随机游走中的功率谱密度设置为1 cm/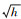
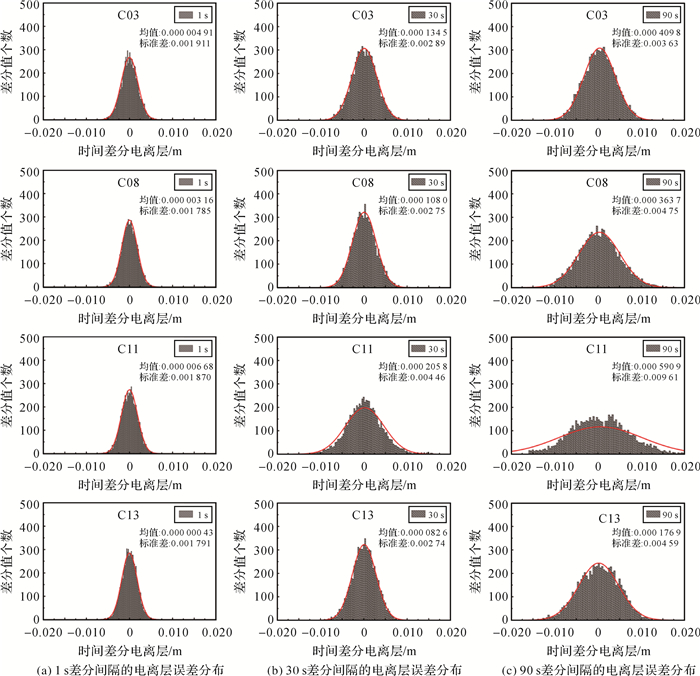
选取Baseline 4基线进行电离层功率谱密度的特性分析,通过式(17)、式(18)求得BDS的不同卫星电离层时间差分后的均值与方差,对不同时间间隔差分电离层进行研究,其中数据段的长度l=7200 s,不同时间间隔差分后的电离层延迟误差正态分布如图 1所示。
|
| 图 1 不同差分时间间隔电离层正态分布 Fig. 1 The normal distribution of the ionosphere at different time intervals |
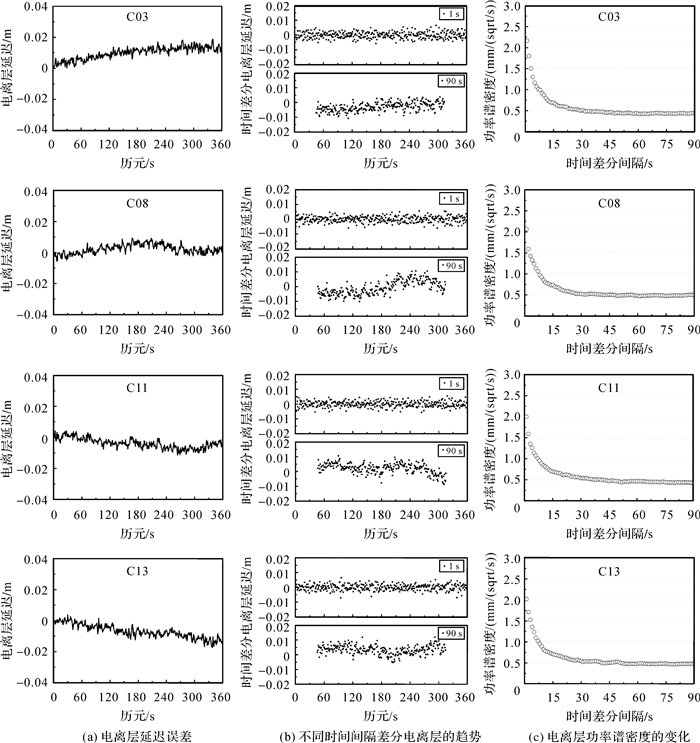
由图 1可以看出,不同差分间隔的电离层延迟均符合正态分布,由图中标注的均值与标准差的数值可以看出,随着差分时间间隔的增大,各颗卫星都表现出了差分电离层均值增大,标准差增大的规律,差分间隔增加到90 s时均值也很小,变化也符合正态分布。为此,本文将电离层参数估计为随机游走,求解时将电离层参数时间变化的均值设置为0,通过得到的功率谱密度来调整电离层参数时间变化的方差。由上文可知,当差分时间间隔不同时,噪声对电离层功率谱密度的影响也不同,为此对不同差分时间间隔下的电离层表现进行研究,图 2为C03、C08、C11、C13卫星电离层延迟误差时间序列、不同时间间隔差分电离层延迟,不同时间间隔求得的功率谱密度。
|
| 图 2 不同差分时间间隔电离层功率谱密度 Fig. 2 IPSD at different differential time intervals |
由图 2可以看出,当差分间隔为1 s时,噪声的影响占主导地位,时间差分电离层延迟不随时间变化,表现出了噪声的白噪声特性,当差分间隔增大到90 s时,此时电离层延迟将占据主导地位,可以看出各颗卫星的时间差分电离层延迟表现出了随着时间变化的随机游走的趋势,可以反映电离层延迟时间变化的大小。各颗卫星的功率谱密度均表现出了随差分时间间隔增大而减小,最后趋于稳定的趋势,这是由于差分间隔增大到一定程度时,时间差分电离层观测值中噪声的影响不显著,电离层的变化占主导地位,此时得到的功率谱密度是电离层本身的特性,不随差分间隔的改变而发生变化,表现出了稳定性。
3.2 Vondrak平滑方法的平滑效果分析本节选取Baseline 4基线进行Vondrak平滑方法的平滑效果分析,移动平滑是平滑中最常使用的方式,为此本文通过移动平滑方法对式(11)的电离层观测值进行平滑,利用Vondrak平滑中的拟合度和平滑度综合分析不同平滑窗口的平滑效果,统计它们之间的拟合度和平滑度,平滑度(smoothness, S)与拟合度(fitness, F)信息见表 2。
| 平滑时间/s | 评价指标 | C03 | C08 | C11 | C13 |
| 1 | 拟合度F | 0 | 0 | 0 | 0 |
| 平滑度S | 569 656.711 | 21 089.474 | 253 693.531 | 2 583 440.173 | |
| 30 | 拟合度F | 8.694 | 2.106 | 2.762 | 2.958 |
| 平滑度S | 469.105 | 163.799 | 260.361 | 2 068.047 | |
| 60 | 拟合度F | 9.679 | 2.341 | 3.427 | 3.214 |
| 平滑度S | 275.709 | 78.766 | 56.215 | 898.843 | |
| 90 | 拟合度F | 10.204 | 2.612 | 4.489 | 3.459 |
| 平滑度S | 243.592 | 68.245 | 40.188 | 614.094 | |
| 120 | 拟合度F | 10.477 | 2.955 | 6.262 | 3.780 |
| 平滑度S | 216.856 | 49.942 | 35.129 | 325.793 |
拟合度反映的是对电离层观测值拟合的程度,拟合度越小,表示拟合效果越优;平滑度则反映的是对电离层观测值中噪声的削弱程度,平滑度越小,削弱效果越好。由表 2可以看出,随着平滑窗口的增大,拟合度由未进行拟合时的0逐渐变大,120 s时达到了拟合度的最大值,此时平滑后的电离层观测值与原始观测值的偏离程度最大。平滑度与拟合度变化趋势正好相反,未进行平滑时,因受噪声的影响,平滑度达到了最大值,随着平滑窗口的增大而逐渐变小,120 s时达到了平滑度的最小值,此时平滑值受噪声的影响最小,拟合曲线越光滑。可以发现,移动平滑方法中拟合度与平滑度呈相反的变化趋势,难以在平滑度与拟合度之间取得平衡,运用Vondrak平滑算法可以较好地解决这个问题,达到最优平滑效果,使得平滑值能在削弱观测噪声的同时反映电离层实时的变化。
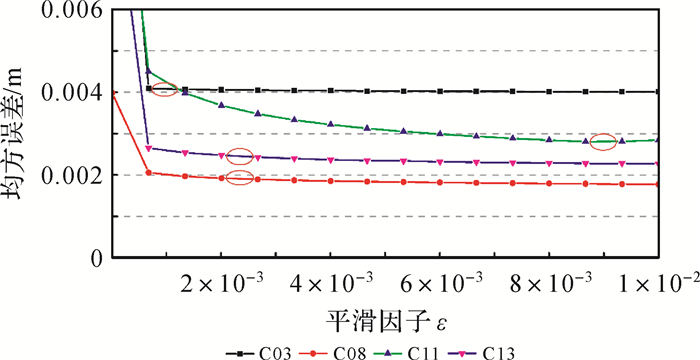
Vondrak平滑算法通过选择合适的平滑因子来平衡对观测噪声的削弱与电离层变化的反映,因电离层观测值的噪声可以通过1 s差分时间间隔观测值反算求得,因此本文通过观测误差法来确定最佳平滑因子。图 3为均方误差随平滑因子的变化曲线。
|
| 图 3 均方误差的变化曲线 Fig. 3 Variation curve of RMSE |
图 3曲线上的圆圈表示最佳平滑因子对应的均方误差值。由图 3可以看出,随着平滑因子的增大,各颗卫星的均方误差都表现出了减小的趋势,表示对电离层观测值的噪声削弱效果越好,同时均方误差的减小趋势变慢,均方误差变化变慢的地方与最佳平滑因子相对应,也进一步表明了本文确定的最佳平滑因子正确性。每颗卫星均方误差变化曲线存在差异,受电离层观测值变化与噪声共同的影响,因此各颗卫星的最佳平滑因子也是不同的。平滑因子的选择与电离层观测值的变化程度及观测值的噪声有关,其中电离层观测值变化程度反映的是拟合度,观测值噪声反映的是平滑度。表 3为最佳平滑因子对应的平滑误差。
| 卫星号 | 最佳平滑因子 | 去噪后均方误差 | 电离层观测值噪声 | 平滑误差 |
| C03 | 1.0×10-3 | 4.021 | 4.464 | 0.443 |
| C08 | 2.5×10-3 | 2.356 | 2.558 | 0.202 |
| C11 | 9.0×10-3 | 2.933 | 2.818 | 0.115 |
| C13 | 2.5×10-3 | 2.551 | 2.891 | 0.340 |
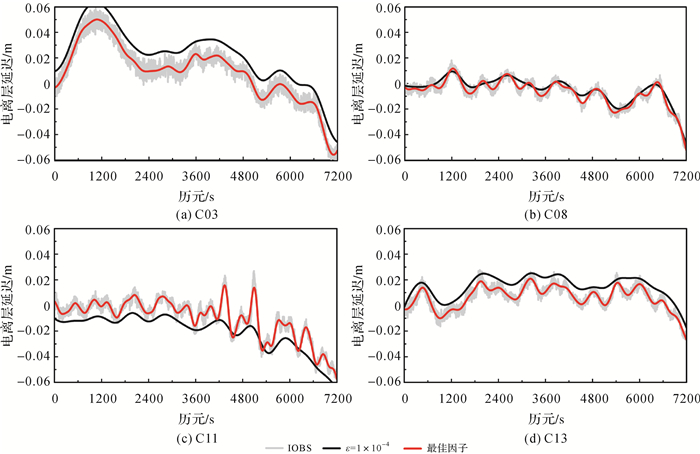
表 3给出了最佳平滑因子的均方误差与电离层观测值噪声之间的差异,电离层观测值的噪声可以通过1 s差分时间间隔电离层观测值反算求得,最佳平滑因子对应的均方误差反映的是观测值的噪声的情况,两者之间存在的差异可以表征平滑的效果,两者越接近,表明平滑效果越好,由表 3可知,各颗卫星平滑误差都保持在0.5 mm内。图 4给出了不同平滑因子对应的电离层平滑时间序列。
|
| 图 4 不同平滑因子电离层平滑值比较 Fig. 4 Comparison of ionospheric smoothing values for different smoothing factors |
图 4中IOBS为未平滑之前的电离层观测值,其余线条表示不同平滑因子平滑后的电离层延迟。由图 4可知,平滑之前的电离层延迟噪声较大,求得的电离层误差存在因噪声引起的随机波动,通过平滑后的电离层表现平稳,最佳平滑因子能在削弱电离层观测噪声的同时,精确地拟合出电离层观测值的变化。
3.3 不同平滑程度对定位性能的影响本文采用了Vondrak平滑方法来对电离层观测值进行平滑,削弱噪声后确定电离层的功率谱密度进行定位。平滑效果决定了平滑后的电离层延迟与真实电离层之间的差异,也将决定求得电离层功率谱密度的准确性。本文以Baseline 4基线为例,采用Vondrak平滑方法及不同窗口的移动平滑方法分析不同平滑程度对BDS三频观测数据定位性能的影响。将Baseline 4中24 h的数据进行每2 h的分割,对12个时段的收敛时间及定位精度求均值后见表 4。
| 平滑窗口 | 收敛速度/s | N/m | E/m | U/m |
| Vondrak平滑 | 213 | 0.015 4 | 0.009 2 | 0.024 7 |
| 1 s | 273 | 0.019 8 | 0.010 3 | 0.032 5 |
| 30 s | 576 | 0.016 8 | 0.008 4 | 0.025 7 |
| 60 s | 225 | 0.017 9 | 0.009 0 | 0.025 3 |
| 90 s | 701 | 0.015 9 | 0.008 2 | 0.027 8 |
| 120 s | 852 | 0.013 7 | 0.009 6 | 0.026 1 |
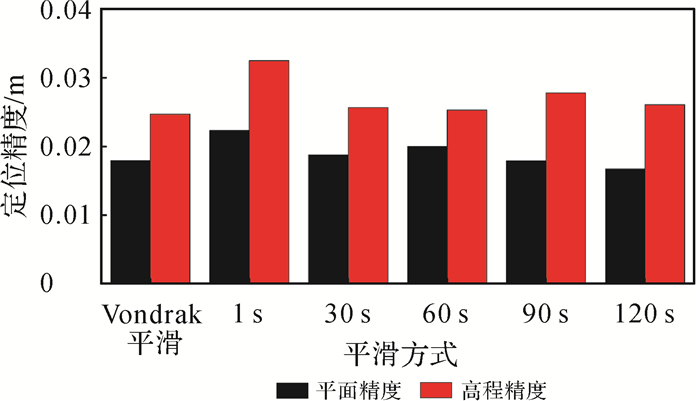
由表 4可知,采用Vondrak平滑方法得到的收敛时间明显优于移动窗口的方法,其中60 s平滑窗口得到的收敛速度是移动平滑方法中最优的,但仍旧不如Vondrak平滑方法,说明了利用Vondrak平滑方法进行电离层观测值平滑的优势。1 s时得到的时间约束信息进行定位,即通过原始观测值得到的电离层功率谱密度,收敛速度较慢,表明通过原始观测值求得的功率谱密度不是最优的。为了更直观地得到不同平滑方式的定位精度,图 5给出了不同平滑方式在平面方向和高程方向的定位精度。
|
| 图 5 不同平滑方式定位精度 Fig. 5 Positioning accuracy of different smoothing methods |
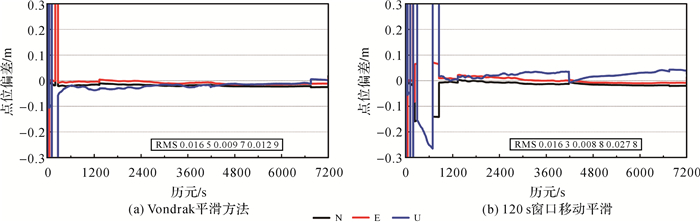
由图 5可知,1 s平滑窗口得到的平面精度和高程精度均不如其他平滑窗口,在高程方向上Vondrak平滑方法是优于移动窗口的方法,而在平面精度上,除1 s移动窗口外,Vondrak平滑方法和移动窗口的方法在定位精度上没有较大差异。图 6给出了其中一个时段通过Vondrak平滑方法及120 s窗口移动平滑间得到的功率谱密度的定位结果。
|
| 图 6 不同平滑程度定位结果比较 Fig. 6 Comparison of positioning results with different smoothness levels |
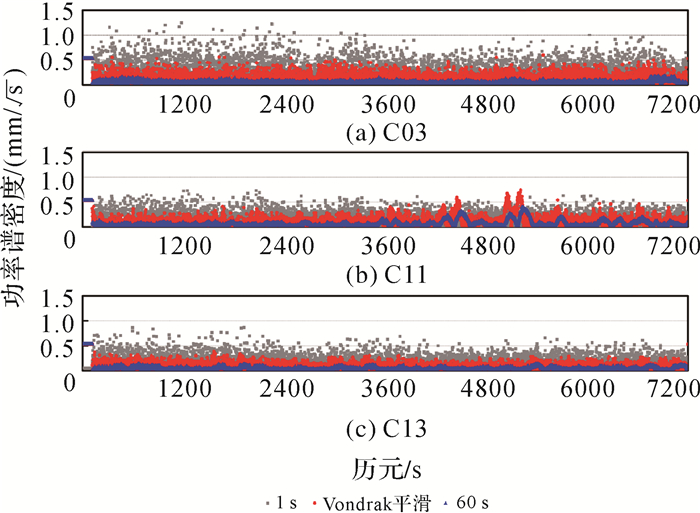
由图 6可知,Vondrak平滑方法3个方向定位的RMS分别为0.016 5、0.009 7、0.012 9 m,而通过120 s平滑窗口得到的定位RMS分别为0.016 3、0.008 8、0.027 8 m,Vondrak平滑方法使得U方向的定位精度得到很大的提升,两种情况下定位结果均可收敛,但收敛速度上两者存在较大差异,Vondrak平滑方法的收敛时间明显较短。由以上分析可以看出,Vondrak平滑方法得到电离层功率谱密度的定位性能优于移动平滑的方式,两种情况下定位结果都可以收敛,但收敛速度上两者存在较大差异。图 7给出了C03、C11、C13卫星采用Vondrak平滑方法及不同窗口的移动平滑方法的功率谱密度时间序列。
|
| 图 7 不同平滑程度的电离层功率谱密度值 Fig. 7 Comparison of IPSD with different smoothness levels |
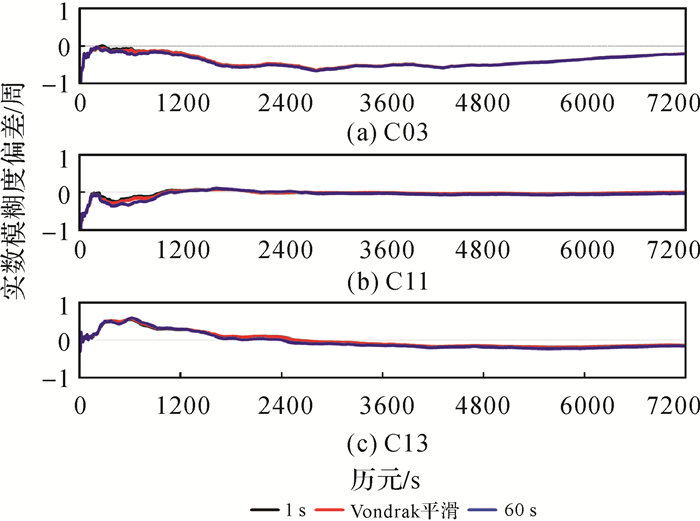
由图 7可以看出,未平滑的1 s电离层观测值得到的功率谱密度随机分布,未表现出变化规律。采用Vondrak平滑方法时,电离层功率谱密度表现出了随时间的变化趋势,特别是C11卫星在电离层变化剧烈时功率谱密度也变大,平滑窗口为60 s时虽然也表现出了电离层的变化趋势,但平滑窗口过大也将忽略电离层局部的变化使得精度变差。图 8为不同卫星的实数模糊度偏差的时间序列。
|
| 图 8 不同平滑程度的模糊度浮点解偏差 Fig. 8 Comparison of float ambiguity bias with different smoothness levels |
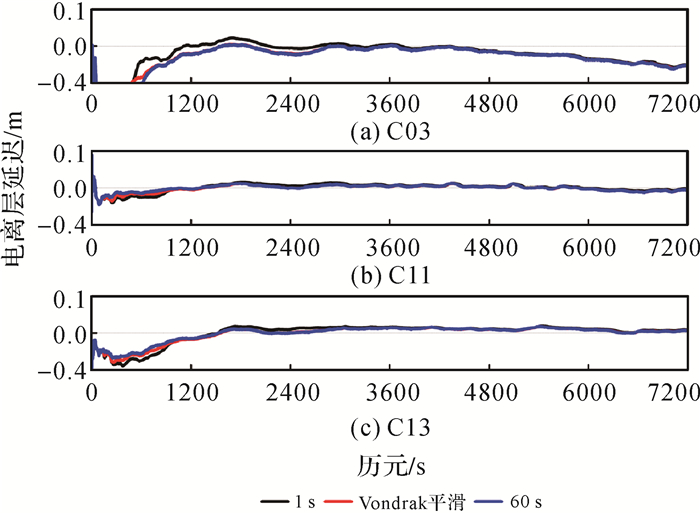
由图 8可以看出,采用Vondrak平滑方法及不同窗口的移动平滑方法在时段前期存在差异,使得模糊度的收敛时间受到影响,从C11卫星的实数解偏差可以看出,Vondrak平滑方法实数解明显优于移动平滑的方式。随着解算时长的增加,后期各种方法的模糊度实数解基本一致。图 9给出了C03、C13、C13的电离层延迟变化的时间序列。
|
| 图 9 不同平滑程度的电离层值 Fig. 9 Comparison of ionospheric values with different smoothness levels |
由图 9中不同平滑窗口的电离层误差序列可以看出,收敛前电离层延迟表现出了较大的差异,特别是C03卫星,1 s平滑窗口得到的电离层延迟与60 s平滑窗口和Vondrak平滑方法得到的电离层延迟存在较大差异,但收敛后电离层表现一致,表明不同方法收敛后得到的电离层变化均能反映电离层的实时变化。
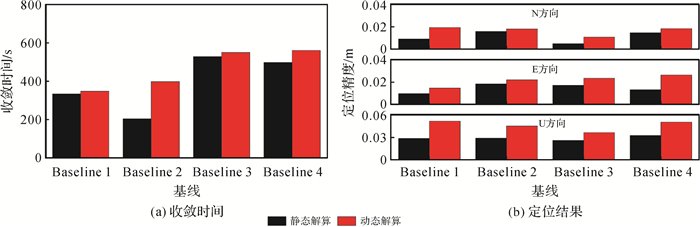
3.4 电离层时变特性约束的BDS定位性能分析由上文可知,通过Vondrak平滑方法能在削弱观测值噪声的同时反映电离层的真实变化,求得更准确的功率谱密度对电离层进行合理的约束,本节通过Vondrak平滑方法确定的功率谱密度对4条基线的BDS三频数据进行静态及动态模式的解算,每2 h一个时段进行收敛时间及定位精度的统计。4条基线的定位结果如图 10所示。
|
| 图 10 不同基线的收敛时间及定位结果 Fig. 10 Convergence time and positioning results of different long baselines |
由图 10可以看出,4条基线均可以实现厘米级的定位精度,静态解算的精度优于动态解算,其中N方向的定位精度在2 cm以内,E方向的定位精度在3 cm内,U方向保持在6 cm内。收敛时间保持在600 s以内,其中Baseline 2静态解算的收敛时间仅为204 s,动静态模式时间差距较大的原因是Baseline 2参与解算的卫星数目明显多于其他3条基线,卫星数多时方程的性质好,使得静态模式能很快收敛,动态模式时每个历元都出现的位置参数影响模糊度的固定,从而动静态收敛时间相差较大。图 11、图 12给出了Baseline 3和Baseline 4基线4个时段静态和动态模式下的定位结果误差序列。
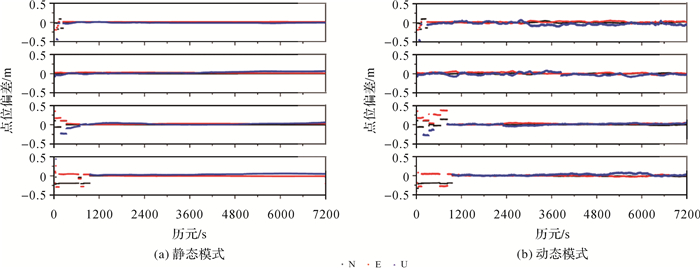
|
| 图 11 Baseline 3静态和动态解算模式定位结果 Fig. 11 Static and dynamic solution mode positioning results of Baseline 3 |
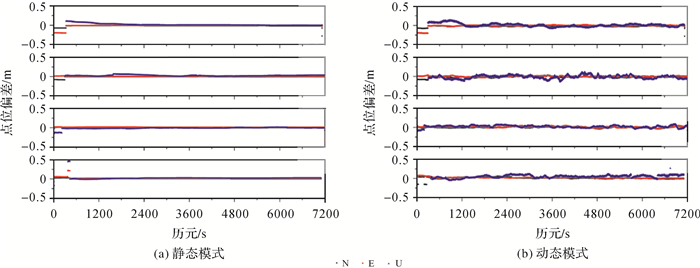
|
| 图 12 Baseline 4静态和动态解算模式定位结果 Fig. 12 Static and dynamic solution mode positioning results of Baseline 4 |
由图 11和图 12给出的两条基线的定位结果误差序列可以看出,收敛后误差序列表现平稳,始终保持在较高的精度。动态模式的误差序列U方向出现小幅度的变化,其高程方向与天顶对流层相关性较强,由于文中对流层的随机游走约束采用了经验值未能很好模拟对流层的变化,使得与U方向分离出现了困难,定位精度不如N、E方向,但仍旧保持着厘米级的定位精度。
4 结论BDS长基线RTK定位时如果采用非组合观测值形式,一般将电离层误差当作参数进行估计,但在未知参数增加的情况下,方程的性质变弱,使得模糊度的收敛时间变长,甚至使得结果发散。本文以载波相位观测值中提取的电离层观测值为研究对象,研究表现电离层时间特性的功率谱密度,与以往对电离层通过建模及采用经验值的约束方式不同,本文得到的电离层时间约束值源自原始观测值,反映的是电离层的实时变化,因此在时间约束方面有较大的优势。本文通过Vondrak滤波对电离层观测值进行最优平滑,在削弱噪声的同时反映电离层的实时变化,以此求得真实的功率谱密度对电离层参数进行时间约束,使得定位性能达到最优。最后利用本文得到的功率谱密度对电离层参数约束进行BDS三频观测值的定位,动态静态模式下均可以达到快速收敛,收敛后精度稳定在厘米级,满足实时动态静态的定位需求。
| [1] |
杨元喜, 李金龙, 徐君毅, 等. 中国北斗卫星导航系统对全球PNT用户的贡献[J]. 科学通报, 2011, 56(21): 1734-1740. YANG Yuanxi, LI Jinlong, XU Junyi, et al. The contribution of BDS to the global PNT users[J]. Chinese Science Bulletin, 2011, 56(21): 1734-1740. |
| [2] |
ZHANG Xiaohong, HE Xiyang. Performance analysis of triple-frequency ambiguity resolution with BeiDou observations[J]. GPS Solutions, 2016, 20(2): 269-281. DOI:10.1007/s10291-014-0434-0 |
| [3] |
TANG Weiming, DENG Chenlong, SHI Chuang, et al. Triple-frequency carrier ambiguity resolution for BeiDou navigation satellite system[J]. GPS Solutions, 2014, 18(3): 335-344. DOI:10.1007/s10291-013-0333-9 |
| [4] |
祝会忠, 李军, 蔚泽然, 等. 长距离GPS/BDS参考站网多频载波相位整周模糊度解算方法[J]. 测绘学报, 2020, 49(3): 300-311. ZHU Huizhong, LI Jun, YU Zeran, et al. The algorithm of multi-frequency carrier phase integer ambiguity resolution with GPS/BDS between long range network RTK reference stations[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(3): 300-311. DOI:10.11947/j.AGCS.2020.20190191 |
| [5] |
LI Bofeng, LI Zhen, ZHANG Zhiteng, et al. ERTK: extra-wide-lane RTK of triple-frequency GNSS signals[J]. Journal of Geodesy, 2017, 91(9): 1031-1047. DOI:10.1007/s00190-017-1006-1 |
| [6] |
ZHU Huizhong, LU Yangyang, TANG Longjiang, et al. A comparative study of BDS triple-frequency ambiguity fixing approaches for RTK positioning[J]. Sensors (Basel, Switzerland), 2021, 21(7): 2565. DOI:10.3390/s21072565 |
| [7] |
祝会忠. 基于非差误差改正数的长距离单历元GNSS网络RTK算法研究[J]. 测绘学报, 2015, 44(1): 116. ZHU Huizhong. The study of GNSS network RTK algorithm between long range at single epoch using undifference error corrections[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(1): 116. DOI:10.11947/j.AGCS.2015.20140358 |
| [8] |
LI Bofeng, SHEN Yunzhong, FENG Yanming, et al. GNSS ambiguity resolution with controllable failure rate for long baseline network RTK[J]. Journal of Geodesy, 2014, 88(2): 99-112. DOI:10.1007/s00190-013-0670-z |
| [9] |
GENG Jianghui, GUO Jiang, CHANG Hua, et al. Toward global instantaneous decimeter-level positioning using tightly coupled multi-constellation and multi-frequency GNSS[J]. Journal of Geodesy, 2019, 93(7): 977-991. DOI:10.1007/s00190-018-1219-y |
| [10] |
ZHANG Ming, LIU Hui, BAI Zhengdong, et al. Fast ambiguity resolution for long-range reference station networks with ionospheric model constraint method[J]. GPS Solutions, 2017, 21(2): 617-626. DOI:10.1007/s10291-016-0551-z |
| [11] |
高扬骏, 吕志伟, 周朋进, 等. 北斗中长基线三频模糊度解算的自适应抗差滤波算法[J]. 测绘学报, 2019, 48(3): 295-302. GAO Yangjun, LÜ Zhiwei, ZHOU Pengjin, et al. Adaptive robust filtering algorithm for BDS medium and long baseline three carrier ambiguity resolution[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(3): 295-302. DOI:10.11947/j.AGCS.2019.20180379 |
| [12] |
李博峰, 沈云中, 周泽波. 中长基线三频GNSS模糊度的快速算法[J]. 测绘学报, 2009, 38(4): 296-301. LI Bofeng, SHEN Yunzhong, ZHOU Zebo. A new method for medium and long range three frequency GNSS rapid ambiguity resolution[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 296-301. |
| [13] |
ZHANG Xiaohong, REN Xiaodong, CHEN Jun, et al. Investigating GNSS PPP-RTK with external ionospheric constraints[J]. Satellite Navigation, 2022, 3(1): 6. DOI:10.1186/s43020-022-00067-1 |
| [14] |
ODIJK D. Weighting ionospheric corrections to improve fast GPS positioning over medium distances[C]//Proceeding of the 13th International Technical Meeting of the Satellite Division of the Institute of Navigation. Salt Lake, UT, USA: [s.n.], 2000.
|
| [15] |
WIELGOSZ P. Quality assessment of GPS rapid static positioning with weighted ionospheric parameters in generalized least squares[J]. GPS Solutions, 2011, 15(2): 89-99. DOI:10.1007/s10291-010-0168-6 |
| [16] |
BASILE F, MOORE T, HILL C, et al. Multi-frequency precise point positioning using GPS and Galileo data with smoothed ionospheric corrections[C]//Proceedings of 2018 IEEE/ION Position, Location and Navigation Symposium. Monterey, CA, USA: IEEE, 2018.
|
| [17] |
TU Rui. A real-time ionospheric model based on GNSS precise point positioning[J]. Advances in Space Research, 2013, 52(6): 1125-1134. DOI:10.1016/j.asr.2013.06.015 |
| [18] |
祝会忠, 雷啸挺, 徐爱功, 等. 顾及GEO卫星约束的长距离BDS三频整周模糊度解算[J]. 测绘学报, 2020, 49(9): 1222-1234. ZHU Huizhong, LEI Xiaoting, XU Aigong, et al. The integer ambiguity resolution of BDS triple-frequency between long range stations with GEO satellite constraints[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(9): 1222-1234. DOI:10.11947/j.AGCS.2020.20200263 |
| [19] |
SHI C, GU S, LOU Y, et al. An improved approach to model ionospheric delays for single-frequency Precise Point Positioning[J]. Advances in Space Research, 2012, 49(12): 1698-1708. DOI:10.1016/j.asr.2012.03.016 |
| [20] |
ZHAO Qile, WANG Yintong, GU Shengfeng, et al. Refining ionospheric delay modeling for undifferenced and uncombined GNSS data processing[J]. Journal of Geodesy, 2019, 93(4): 545-560. DOI:10.1007/s00190-018-1180-9 |
| [21] |
ALBASHIR A, ABDELLATIF SAMI K, AHMEDELTIGANI M. Enhancing the accuracy of GPS point positioning by modeling the ionospheric propagation delay[C]//Proceedings of 2018 International Conference on Computer, Control, Electrical, and Electronics Engineering (ICCCEEE). Khartoum, Sudan: IEEE, 2018.
|
| [22] |
周锋, 徐天河. GPS/BDS/Galileo三频精密单点定位模型及性能分析[J]. 测绘学报, 2021, 50(1): 61-70. ZHOU Feng, XU Tianhe. Modeling andassessment of GPS/BDS/Galileo triple-frequency precise point positioning[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(1): 61-70. DOI:10.11947/j.AGCS.2021.20200146 |
| [23] |
葛茂荣, 刘经南. GPS定位中对流层折射估计研究[J]. 测绘学报, 1996, 25(4): 285-291. GE Maorong, LIU Jingnan. The estimation methods for tropospheric delays in global positioning system[J]. Acta Geodaetica et Cartographica Sinica, 1996, 25(4): 285-291. |
| [24] |
FAN Haopeng, SUN Zhongmiao, ZHANG Liping, et al. A two-step estimation method of troposphere delay with consideration of mapping function errors[J]. Journal of Geodesy and Geoinformation Science, 2020, 3(1): 76-84. |
| [25] |
毛健, 崔铁军, 李晓丽, 等. 融合大气数值模式的高精度对流层天顶延迟计算方法[J]. 测绘学报, 2019, 48(7): 862-870. MAO Jian, CUI Tiejun, LI Xiaoli, et al. A hight-accuracy method for tropospheric zenith delay error correction by fusing atmospheric numerical models[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(7): 862-870. DOI:10.11947/j.AGCS.2019.20190003 |
| [26] |
TANG Weiming, LIU Wenjian, ZOU Xuan, et al. Improved ambiguity resolution for URTK with dynamic atmosphere constraints[J]. Journal of Geodesy, 2016, 90(12): 1359-1369. DOI:10.1007/s00190-016-0928-3 |
| [27] |
ZHANG Baocheng, HOU Pengyu, ZHA Jiuping, et al. PPP-RTK functional models formulated with undifferenced and uncombined GNSS observations[J]. Satellite Navigation, 2022, 3(1): 1-15. DOI:10.1186/s43020-022-00063-5 |
| [28] |
陈正生, 张清华, 李林阳, 等. 电离层延迟变化自模型化的载波相位平滑伪距算法[J]. 测绘学报, 2019, 48(9): 1107-1118. CHEN Zhengsheng, ZHANG Qinghua, LI Linyang, et al. An improved carrier phase smoothing pseudorange algorithm with self-modeling of ionospheric delay variation[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(9): 1107-1118. DOI:10.11947/j.AGCS.2019.20180404 |
| [29] |
ZHU Huizhong, LI Jun, TANG Longjiang, et al. Improving the stochastic model of ionospheric delays for BDS long-range real-time kinematic positioning[J]. Remote Sensing, 2021, 13(14): 2739. DOI:10.3390/rs13142739 |
| [30] |
VONDRAK J. Problem of Smoothing Observation Data Ⅱ[J]. Bulletin of the Astronomical Institute of Czechoslovakia, 1977, 28(2): 84-89. |
| [31] |
VONDRAK J. Problem of Smoothing Observation Data[J]. Bulletin of the Astronomical Institute of Czechoslovakia, 1969, 20(6): 349-353. |
| [32] |
ZHENG D W, ZHONG P, DING X L, et al. Filtering GPS time-series using a Vondrak filter and cross-validation[J]. Journal of Geodesy, 2005, 79(6): 363-369. |
| [33] |
VONDRAK J. A contribution to the problem of smoothing observational data[J]. Bulletin of the Astronomical Institutes of Czechoslovakia, 1969, 20(6): 349. |
| [34] |
吴芸芸, 朱建军, 左廷英. RMSE的平方与平滑度的线性组合的平方根作为Vondrak滤波评价标准的探讨[J]. 武汉大学学报(信息科学版), 2012, 37(10): 1212-1214, 1220. WU Yunyun, ZHU Jianjun, ZUO Tingying. Investigation on the square root of the linear combination of the squre of RMSE and smoothness for the vondrak filter's evaluation[J]. Geomatics and Information Science of Wuhan University, 2012, 37(10): 1212-1214, 1220. |



