





测绘学报 ›› 2024, Vol. 53 ›› Issue (11): 2178-2188.doi: 10.11947/j.AGCS.2024.20240027
收稿日期:2024-01-06
出版日期:2024-12-13
发布日期:2024-12-13
作者简介:第一胡川(1983—),男,博士,副教授,研究方向为测量数据处理理论与方法。 E-mail:hucch@cqjtu.edu.cn
基金资助:
Chuan HU( ), Zonghao SHI, Daqin REN
), Zonghao SHI, Daqin REN
Received:2024-01-06
Online:2024-12-13
Published:2024-12-13
About author:HU Chuan (1983—), male, PhD, associate professor, majors in the theory and methods of measurement data processing. E-mail: hucch@cqjtu.edu.cn
Supported by:摘要:
通用非线性高斯-赫尔默特模型是顾及因变量或全体变量误差的显式和隐式非线性函数平差模型的统一表达。针对在迭代初值与真值相差较大时,高斯-牛顿迭代解算法存在不收敛的问题,本文提出融合同伦方法与非线性最小二乘的通用非线性高斯-赫尔默特模型参数估计法。从引入同伦参数的非线性最小二乘平差准则出发,推导了求解通用模型参数的微分方程组和追踪同伦曲线的固定步长预测公式与牛顿校正公式,给出了隐式函数模型残差向量的近似计算公式。为避免计算立体矩阵,将克罗内克积和矩阵拉直运算引入推导过程,降低了计算微分方程组的复杂度。通过仅顾及自变量误差的距离定位、顾及卫星坐标误差和测距误差的伪距定位、顾及全体平面坐标误差的圆曲线拟合,以及顾及已知坐标误差的测边网平差4个试验,对本文方法的可行性进行了验证。试验结果表明:在设定的两组初值中,当高斯-牛顿法收敛时,本文方法也收敛;当高斯-牛顿法不收敛时,本文方法仍收敛;本文方法收敛的初值范围更大。
中图分类号:
胡川, 史宗浩, 任大钦. 通用非线性高斯-赫尔默特模型参数估计的同伦方法[J]. 测绘学报, 2024, 53(11): 2178-2188.
Chuan HU, Zonghao SHI, Daqin REN. On homotopy method to parameter estimation for generalized nonlinear Gauss-Helmert model[J]. Acta Geodaetica et Cartographica Sinica, 2024, 53(11): 2178-2188.
表3
通用同伦平差结果(算例2)"
| 参数项 | 采用初值1 | 采用初值2 | ||
|---|---|---|---|---|
| 高斯-牛顿法 | 通用同伦平差法 | 高斯-牛顿法 | 通用同伦平差法 | |
| Xu/m | -2 157 555.665 | -2 157 555.665 | ||
| Yu/m | 4 380 372.532 | 4 380 372.532 | ||
| Zu/m | 4 081 041.770 | 4 081 041.770 | ||
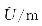 | 175 322.286 | 175 322.286 | ||
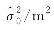 | 不收敛 | 137 879 264.216 | 不收敛 | 137 879 264.215 |
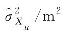 | 293 314 174.167 | 293 314 174.167 | ||
 | 336 342 488.338 | 336 342 488.338 | ||
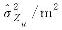 | 266 625 946.277 | 266 625 946.277 | ||
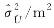 | 240 957 927.393 | 240 957 927.393 | ||
表7
坐标估计值(算例4)"
| 坐标 | 采用初值1 | 采用初值2 | ||
|---|---|---|---|---|
| 高斯-牛顿法 | 通用同伦平差法 | 高斯-牛顿法 | 通用同伦平差法 | |
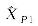 | 9 034.167 03 | 9 034.167 03 | 8 551.905 79 | |
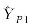 | 907.528 22 | 907.528 22 | 534.879 53 | |
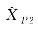 | 8 762.945 47 | 8 762.945 47 | 8 410.402 64 | |
 | 1 124.473 48 | 1 124.473 48 | 发散 | 852.059 65 |
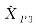 | 9 221.056 88 | 9 221.056 88 | 8 407.059 58 | |
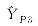 | 1 008.491 04 | 1 008.491 04 | 379.506 16 | |
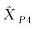 | 9 031.113 45 | 9 031.113 45 | 8 129.022 37 | |
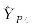 | 1 345.343 85 | 1 345.343 85 | 648.287 90 | |
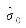 | 0.001 87 | 0.001 87 | 0.001 87 | |
| [1] | HU Yu, FANG Xing. Linear estimation under the Gauss-Helmert model: geometrical interpretation and general solution[J]. Journal of Geodesy, 2023, 97(5): 44. |
| [2] | NEITZEL F. Generalization of total least-squares on example of unweighted and weighted 2D similarity transformation[J]. Journal of Geodesy, 2010, 84(12): 751-762. |
| [3] | KANATANI K, NIITSUMA H. Optimal computation of 3D similarity: Gauss-Newton vs. Gauss-Helmert[J]. Computational Statistics & Data Analysis, 2012, 56(12): 4470-4483. |
| [4] | OSADA E, OWCZAREK-WESOŁOWSKA M, SOŚNICA K. Gauss-Helmert model for total station positioning directly in geocentric reference frame including GNSS reference points and vertical direction from earth gravity model[J]. Journal of Surveying Engineering, 2019, 145(4): 04019013. |
| [5] | KOCH K R. Outlier detection for the nonlinear Gauss Helmert model with variance components by the expectation maximization algorithm[J]. Journal of Applied Geodesy, 2014, 8(3): 185-194. |
| [6] | WANG Bin, ZHAO Zhisheng, CHEN Yu, et al. A novel robust point cloud fitting algorithm based on nonlinear Gauss-Helmert model[J]. IEEE Transactions on Instrumentation Measurement, 2023, 72: 3239630. |
| [7] | KARGOLL B, OMIDALIZARANDI M, ALKHATIB H. Adjustment of Gauss-Helmert models with autoregressive and student errors[C]//Proceedings of 2020 Hotine-Marussi Symposium on Mathematical Geodesy. Cham: Springer, 2020: 79-87. |
| [8] | ZHU Jianjun, WANG Leyang, HU Jun, et al. Recent advances in the geodesy data processing[J]. Journal of Geodesy and Geoinformation Science, 2023, 6(3): 33-45. |
| [9] | 吕志鹏, 隋立芬. 基于非线性高斯-赫尔默特模型的结构总体最小二乘法[J]. 武汉大学学报(信息科学版), 2019, 44(12): 1808-1815. |
| LÜ Zhipeng, SUI Lifen. A structured total least squares method based on nonlinear Gauss-Helmert model[J]. Geomatics and Information Science of Wuhan University, 2019, 44(12): 1808-1815. | |
| [10] |
方兴, 曾文宪, 刘经南, 等. 基于非线性高斯-赫尔默特模型的混合整体最小二乘估计[J]. 测绘学报, 2016, 45(3): 291-296. DOI:.
doi: 10.11947/j.AGCS.2016.20150157 |
|
FANG Xing, ZENG Wenxian, LIU Jingnan, et al. Mixed LS-TLS estimation based on nonlinear Gauss-Helmert model[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(3): 291-296. DOI:.
doi: 10.11947/j.AGCS.2016.20150157 |
|
| [11] | 刘春阳, 刘超. 三维坐标转换的非线性Gauss-Helmert模型及其解法[J]. 测绘科学, 2017, 42(5): 118-123. |
| LIU Chunyang, LIU Chao. Nonlinear Gauss-Helment model and its solution for 3D coordinate transformation[J]. Science of Surveying and Mapping, 2017, 42(5): 118-123. | |
| [12] | WANG Bin, FANG Xing, LIU Chao, et al. Data snooping for the equality constrained nonlinear Gauss-Helmert model using sensitivity analysis[J]. Journal of Surveying Engineering, 2020, 146(4): 04020015. |
| [13] | KOCH K R. Robust estimations for the nonlinear Gauss Helmert model by the expectation maximization algorithm[J]. Journal of Geodesy, 2014, 88(3): 263-271. |
| [14] | 刘超, 王彬, 赵兴旺, 等. 三维坐标转换的高斯-赫尔默特模型及其抗差解法[J]. 武汉大学学报(信息科学版), 2018, 43(9): 1320-1327. |
| LIU Chao, WANG Bin, ZHAO Xingwang, et al. Three-dimensional coordinate transformation model and its robust estimation method under Gauss-Helmert model[J]. Geomatics and Information Science of Wuhan University, 2018, 43(9): 1320-1327. | |
| [15] | 赵志胜, 陈宇, 王彬. 利用非线性高斯-赫尔默特模型与抗差估计的点云拟合方法[J]. 武汉大学学报(信息科学版), 2024, 49(7): 1201-1211. |
| ZHAO Zhisheng, CHEN Yu, WANG Bin. Point cloud fitting method using the nonlinear Gauss-Helmert model and robust estimation[J]. Geomatics and Information Science of Wuhan University, 2024, 49(7): 1201-1211. | |
| [16] | 邝英才, 吕志平, 李林阳, 等. GNSS-A水下定位的动态非线性Gauss-Helmert模型及其抗差总体卡尔曼滤波算法[J]. 测绘学报, 2023, 52(4): 559-570. |
| KUANG Yingcai, LÜ Zhiping, LI Linyang, et al. Dynamic nolinear Gauss-Helmert model and its robust total Kalman filter algorithm for GNSS-acoustic underwater positioning[J]. Acta Geodaetica et Cartographica Sinica, 2023, 52(4): 559-570. | |
| [17] | KUANG Yingcai, LÜ Zhiping, WANG Fangchao, et al. A nonlinear Gauss-Helmert model and its robust solution for seafloor control point positioning[J]. Marine Geodesy, 2023, 46(1): 16-42. |
| [18] | VOGEL S, ERNST D, NEUMANN I, et al. Recursive Gauss-Helmert model with equality constraints applied to the efficient system calibration of a 3D laser scanner[J]. Journal of Applied Geodesy, 2022, 16(1): 37-57. |
| [19] | ZHOU Tengfei, LIN Peng, ZHANG Songlin, et al. A novel sequential solution for multi-period observations based on the Gauss-Helmert model[J]. Measurement, 2022, 193: 110916. |
| [20] | KARIMINEJAD M M, SHARIFI M A, AMIRI-SIMKOOEI A R. Tikhonov-regularized weighted total least squares formulation with applications to geodetic problems[J]. Acta Geodaetica et Geophysica, 2022, 57(1): 23-42. |
| [21] | 张勤, 黄观文. 非线性最小二乘理论及其在GPS定位中应用研究[M]. 北京: 测绘出版社, 2019. |
| ZHANG Qin, HUANG Guanwen. Research on nonlinear least squares theory and application in GPS positioning[M]. Beijing: Surveying and Mapping Press, 2019. | |
| [22] | 陶本藻, 张勤. GPS非线性数据处理的同伦最小二乘模型[J]. 武汉大学学报(信息科学版), 2003, 28(S1): 115-118. |
| TAO Benzao, ZHANG Qin. Homotopy least squares model for GPS nonlinear data processing[J]. Geomatics and Information Science of Wuhan University, 2003, 28(S1): 115-118. | |
| [23] | 张勤, 陶本藻. 基于同伦法的非线性最小二乘平差统一模型[J]. 武汉大学学报(信息科学版), 2004, 29(8): 708-710. |
| ZHANG Qin, TAO Benzao. Uniform model of nonlinear least squares adjustment based on homotopy method[J]. Geomatics and Information Science of Wuhan University, 2004, 29(8): 708-710. | |
| [24] | 胡志刚, 花向红, 李昭, 等. 基于同伦方法的非线性测量模型参数估计[J]. 武汉大学学报(信息科学版), 2008, 33(9): 930-933. |
| HU Zhigang, HUA Xianghong, LI Zhao, et al. Nonlinear surveying model parameters estimation based on homotopy arithmetic[J]. Geomatics and Information Science of Wuhan University, 2008, 33(9): 930-933. | |
| [25] | 胡志刚, 花向红, 李海英. 基于同伦算法的非线性坐标转换模型研究[J]. 测绘工程, 2008, 17(6): 24-28. |
| HU Zhigang, HUA Xianghong, LI Haiying. Non-linear coordinate transformation method based on homotopy arithmetic[J]. Engineering of Surveying and Mapping, 2008, 17(6): 24-28. | |
| [26] | 游为, 范东明, 黄瑞金. 适用于任意旋转角的三维直角坐标转换方法[J]. 测绘科学, 2009, 34(5): 154-155. |
| YOU Wei, FAN Dongming, HUANG Ruijin. A method of 3D rectangular coordinate transformation adapted to any rotation angle[J]. Science of Surveying and Mapping, 2009, 34(5): 154-155. | |
| [27] | 游为, 范东明. 基于改进同伦算法的非线性最小二乘平差[J]. 西南交通大学学报, 2009, 44(2): 181-185. |
| YOU Wei, FAN Dongming. Nonlinear least squares adjustment based on improved homotopy algorithm[J]. Journal of Southwest Jiaotong University, 2009, 44(2): 181-185. | |
| [28] | 欧阳全欢. 非线性同伦最小二乘理论研究及其应用[D]. 成都: 西南交通大学, 2010. |
| OUYANG Quanhuan. The study and application of nonlinear homotopy least squares theory[D]. Chengdu: Southwest Jiaotong University, 2010. | |
| [29] | 游为, 范东明, 傅淑娟. 同伦函数与填充函数相结合的非线性最小二乘平差模型[J]. 武汉大学学报(信息科学版), 2010, 35(2): 185-188. |
| YOU Wei, FAN Dongming, FU Shujuan. Nonlinear least squares adjustment based on homotopy functions and filled functions[J]. Geomatics and Information Science of Wuhan University, 2010, 35(2): 185-188. | |
| [30] | 刘伟科, 刘国林, 陶秋香. 基于同伦算法的非线性最小二乘相位解缠[J]. 测绘科学, 2012, 37(4): 126-128, 137. |
| LIU Weike, LIU Guolin, TAO Qiuxiang. Nonlinear least squares phase unwrapping based on homotopy method[J]. Science of Surveying and Mapping, 2012, 37(4): 126-128, 137. | |
| [31] | 唐利民, 朱建军. 不适定非线性最小二乘问题的正则化同伦法及其应用[J]. 大地测量与地球动力学, 2010, 30(6): 51-56. |
| TANG Limin, ZHU Jianjun. Regularized homotopy method for ill posed nonlinear least squares problems and its application[J]. Geodesy and Geodynamics, 2010, 30(6): 51-56. | |
| [32] | 唐利民. 非线性最小二乘的不适定性及算法研究[D]. 长沙: 中南大学, 2011. |
| TANG Limin. Research on the ill-posed and solving methods of nonlinear least squares problem[D]. Changsha: Central South University, 2011. | |
| [33] | 惠兴杰, 李霞, 陈一鸣. 一种新的基于Matlab环境的同伦路径跟踪算法[J]. 东北大学学报(自然科学版), 2007, 28(5): 620-622. |
| HUI Xingjie, LI Xia, CHEN Yiming. A new homotopic path-tracking algorithm based on Matlab[J]. Journal of Northeastern University (Natural Science), 2007, 28(5): 620-622. | |
| [34] | 王则柯, 高堂安. 同伦方法引论[M]. 重庆: 重庆出版社, 1990. |
| WANG Zeke, GAO Tang'an. An introduction to homotopy method[M]. Chongqing: Chongqing Publishing Group, 1990. | |
| [35] | 刘国林, 姜岩, 陶华学. 非线性最小二乘参数平差[J]. 测绘学报, 1998, 27(3): 38-44. |
| LIU Guolin, JIANG Yan, TAO Huaxue. Nonlinear least squares adjustment by parameters[J]. Acta Geodaetica et Cartographica Sinica, 1998, 27(3): 38-44. | |
| [36] | XUE shuqiang, YANG Yuanxi, DANG Yamin. Barycentre method for solving distance equations[J]. Survey Review, 2016, 48(348): 188-194. |
| [37] | 薛树强, 杨元喜, 党亚民. 测距定位方程非线性平差的封闭牛顿迭代公式[J]. 测绘学报, 2014, 43(8): 771-777. |
| XUE Shuqiang, YANG Yuanxi, DANG Yamin. A closed-form of Newton iterative formula for nonlinear adjustment of distance equations[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(8): 771-777. | |
| [38] | XU Peiliang. Fast and almost unbiased weighted least squares fitting of circles[J]. Measurement, 2023, 206: 112294. |
| [39] | FANG Xing. On non-combinatorial weighted total least squares with inequality constraints[J]. Journal of Geodesy, 2014, 88(8): 805-816. |
| [40] | WANG Bin, ZHAO Zhisheng, WANG Shuai, et al. Robust LS-VCE for the nonlinear Gauss-Helmert model: case studies for point cloud fitting and geodetic symmetric transformation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2024, 62: 3352920. |
| [41] | FANG Xing, HU Yu, ZENG Wenxian, et al. Weighted least-squares fitting of circles with variance component estimation[J]. Mea-surement, 2022, 205: 112132. |
| [42] | SNOW K B. Topics in total least-squares adjustment within the errors-in-variables model: singular cofactor matrices and prior information[D]. Columbus: The Ohio State University, 2012. |
| [43] | FANG Xing. Weighted total least squares solutions for applications in geodesy[D]. Hannover: Gottfried Wilhelm Leibniz Universität, 2011. |
| [44] | FANG Xing. Weighted total least squares: necessary and sufficient conditions, fixed and random parameters[J]. Journal of Geodesy, 2013, 87(8): 733-749. |
| [45] | HU Yu, FANG Xing, QIN Yuxin, et al. Weighted geometric circle fitting for the Brogar Ring: parameter-free approach and bias analysis[J]. Measurement, 2022, 192: 110832. |
| [1] | 方兴, 曾文宪, 刘经南, 姚宜斌, 王勇. 基于非线性高斯-赫尔默特模型的混合整体最小二乘估计[J]. 测绘学报, 2016, 45(3): 291-296. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||