2. 自然资源部海洋测绘重点实验室, 山东 青岛 266061;
3. 武汉大学卫星导航定位技术研究中心, 湖北 武汉 430079;
4. 国家卫星导航定位技术研究中心, 湖北 武汉 430079;
5. 武汉大学测绘学院, 湖北 武汉 430079;
6. 河海大学地球科学与工程学院, 江苏 南京 211100
2. Key Laboratory of Oceanic Surveying and Mapping, Ministry of Natural Resources, Qingdao 266061, China;
3. GNSS Research Center, Wuhan University, Wuhan 430079, China;
4. National Engineering Center for Satellite Positioning System, Wuhan 430079, China;
5. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
6. School of Earth Sciences and Engineering, Hohai University, Nanjing 211100, China
海洋占地球表面积71%,平均深度3700 m,是全球80%火山和地震的发生地,通过海气交换影响着全球环境和气候变化,同时,其中蕴含的丰富自然资源为世界经济发展和人口增长提供了保障[1]。因此,精准地感知海洋动态和开发利用海洋资源已经成为人类文明延续和发展的关键[2]。我国是一个海洋大国,拥有300多万平方千米的“海洋国土”,如今正向“建设海洋强国”的战略目标阔步前行。由于人类的一切海洋活动(海底资源勘探、水下航行器导航、水下结构监测、水下工程施工、海底地壳的变形测量及大陆架滑坡的监测等任务)均离不开大地测量基准及定位导航技术,因此,海洋战略的实施需海洋位置服务体系的支撑[2-9]。
GNSS可为地表和近地空间设备提供位置服务,然而电磁波在海水中衰减严重,使其无法直接应用于水下的空间。目前,为海洋活动提供位置服务的海洋时空基准网工程建设领域尚属空白[2-8]。基于声波可以在海洋中有效长距离传播的原理,GNSS-声学技术成为构建海洋时空基准并进行水下位置服务的关键技术。现阶段,GNSS-声学定位主要应用于监测海底板块位移,服务于海洋灾害监测和海洋科学研究[10-15]。该应用将包含数个应答器(3、4或6个)的阵列作为一个海底基准站布设在海底板块交界处[16],阵列中应答器均匀分布于海底的一个半径与水深正相关的圆上,测船固定在阵列中心正上方进行静态测量[10, 17-20]或沿预定航迹在阵列上方进行动态测量[21-26]。这类技术只关注于应答器阵列的位移矢量,不强调单个应答器的绝对位置。海洋时空基准网中,单个应答器就是一个独立的位置基准,因此,现阶段GNSS-声学定位研究成果不能直接应用于海底大地控制点的建设,也不能够直接提供水下的位置服务。
为进行高精度GNSS-声学位置服务,需对其中最主要的误差源(声速误差)展开研究。海洋声速随环境在空间域和时间域发生变化:空间域主要呈现垂向分层结构[27-28],时间域受潮汐和内波等影响呈现周期性变化[17, 29-30]。一般情况下,需要在作业海域以一定时空分辨率进行声速剖面的测量。为了进行声速误差精细化处理,还需构建海洋声速场,以削弱声速代表性误差[31]。海洋声速场通常采用经验正交函数(empirical orthogonal function, EOF)方法进行构建:文献[32]基于大西洋跨度近10 a约9万条声速剖面,利用EOF方法构建了水深500 m内的声速场时空模型,分析了海洋物理特征变化;文献[33]基于有限声速剖面数据,提出基于EOF系数空间曲面内插的局域声速场构建方法,建模精度优于0.5 m/s;文献[34]对EOF模型第一模态的时空变化规律进行分析,得出温度是影响第一模态函数时域变化的主要因素。上述研究未考虑声速剖面深度不统一时,声速场构建方法及其应用于GNSS-声学定位的情况。
为了在GNSS-声学定位过程中削弱声速误差的影响,众多学者基于一条参考声速剖面,利用时域观测方程附加声速时域变化参数进行定位解算[19, 20, 23, 35-43]。其中,声速时域变化参数基于平滑约束条件,利用多项式、三次样条函数或三角函数来提取。然而,该类方法需要基于声线跟踪原理,利用相对准确的声速剖面及长时间的声学时延观测数据进行定位解算,不利于水下位置服务实现。为此,国内众多学者尝试对GNSS-声学定位过程进行改进。文献[44—48]提出了多种基于入射角的随机模型,抑制大入射角条件下误差对定位结果的影响。文献[49—53]研究了声线跟踪算法的优化方法。文献[54—56]研究了构建声速改正表或声速改正模型来代替定位过程中声线跟踪环节的方法,提高了定位效率。文献[57—59]研究了利用声速剖面的先验信息反演声速值或声速剖面,进而直接进行定位解算的方法。文献[60—68]从函数模型层面研究了对声速误差、时延误差及杆臂矢量偏心误差等系统误差直接进行参数解算的方法,削弱了其对水下定位的影响。为简化处理过程并同时克服观测值误差的影响,文献[69]将GNSS差分技术思路引入水下定位,组成新的观测值进行目标位置估算,即水声差分定位。文献[26, 64, 70—72]对水下声学差分的优劣及其实际定位效果进行了分析。文献[73]推导了水下差分解和非差解的转换公式,证明了两组解的等价性。然而,对于缺乏声速剖面观测数据及先验声速场的情况,上述方法均不能很好地解决水下高精度GNSS-声学位置服务的问题。
本文针对声速剖面的类型不同时构建声速场并确定海底控制点高精度位置的问题,以及声速信息缺乏条件下进行水下高精度的GNSS-声学位置服务的问题,研究声速剖面时域变化分层模型的构建方法,提出GNSS-声学位置增强服务方法,并面向水下潜器的位置服务研究了海洋声速剖面的层析方法,最后基于南海水深3000 m海域的实测数据对上述方法的有效性进行验证。
1 声速误差的修正方法 1.1 声速剖面时域变化分层模型EOF分解法是一种分析矩阵结构的方法,借助特征向量将矩阵数据分解为随空间变化的空间函数和随时间变化的时间函数。将其应用于海洋声速场模型构建,具体步骤如下:
(1) 对试验期间测的n组声速剖面c(z)进行整理,将各剖面按相同分层依据划为m-1层,共m×n个声速数据。将不同剖面各层交界处声速值减去所有剖面在该交界处声速算术平均值的结果用于表征声速变化的不确定量。因此,tj时刻深度为zi(第i层上界面)处声速值表示为cj(zi),它与所有剖面在该处的声速均值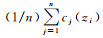
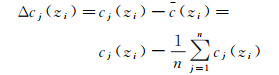 (1)
(1)
令
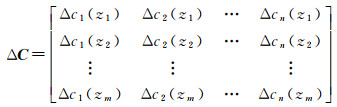 (2)
(2)
(2) 声速的协方差矩阵表示为
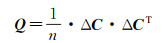 (3)
(3)
利用特征值和特征向量对矩阵Q进行分解,可得
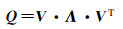 (4)
(4)
式中,Λ为Q的特征值(λ1, λ2, …, λm)组成的对角矩阵;V是Q的特征向量(v1, v2, …, vm)组成的矩阵,每个特征向量为一个EOF模态。
(3) 将Q的特征值按从大到小排列,并定义各特征值λi对应特征向量对矩阵ΔC的贡献表达为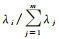
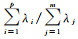
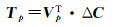 (5)
(5)
式中,矩阵Tp的行向量为对应特征向量的时间系数。由于Vp矩阵的列向量间和Tp矩阵的行向量间均具有正交的特性,因此可便捷地建立模型进行分析。
进而测得的声速剖面可表达为
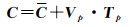 (6)
(6)
式中,C为由Cj组成的声速矩阵;C为由c(zi)组成的平均声速剖面矩阵;Vp为从Q特征向量中挑选的向量所构成的矩阵,可看作固定矩阵,只需对Tp矩阵进行分析即可。
(4) 若同时顾及声速剖面Cj的时刻和水平位置,则Tp可表示为声速剖面时间信息和位置信息构成的矩阵与系数矩阵的乘积。对于局部海域在短时间内的情况,声速场的构建问题可简化为声速剖面时变模型的构建问题。由于海水表层温度随地球自转呈周期性的变化,且声速与温度之间存在近似的线性关系[34],因此认为海洋声速存在以天为周期的变化规律。此时,可用天内秒数作为声速剖面的时刻标签ti,将Tp表示为
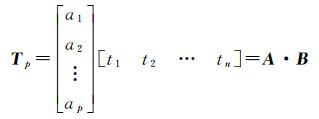 (7)
(7)
根据最小二乘原理可解得矩阵A为
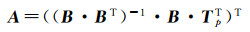 (8)
(8)
(5) 用待求时刻ti构成bi矩阵,便可以求出所需声速剖面
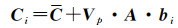 (9)
(9)
由于海试过程中通常综合采用声速剖面仪(sound velocity profiler, SVP)、温盐深测量仪(conductivity-temperature-depth profiler, CTD)、抛弃式温盐深测量仪(expendable conductivity-temperature-depth profiler, XCTD) 或者抛弃式温度测量仪(expendable bathythermograph profiler, XBT)进行声速剖面的测量。其中,XBT实测剖面的最深值一般为300~760 m,XCTD实测剖面的最深值一般为1000~2000 m,SVP和CTD实测剖面的最深值可达全海深,因此综合利用上述的剖面进行EOF建模时会导致“短板效应”[74],即参与建模的最短剖面会限制模型的最深值。由于海洋可按温度变化规律分为混合层、温跃层及深海等温层。其中,混合层底部最深值约为200 m;温跃层与深海等温层的交界面为深海声道轴(声速最小处的深度),约为1000 m[28]。因此,根据海洋结构可将全海深(2900 m)的海洋分为1~200 m、200~1000 m及1000~2900 m共3层。考虑到不同深度区间的声速变化规律不同,且不同声速剖面测量传感器的最大采样深度不同,因此为了保证分层的合理性并充分利用局部海域实测的不同类型声速剖面数据,本文将深度区间层调整为1~250 m、150~750 m、650~1050 m、950~1500 m、1400~2000 m及1900~2900 m共6层。按上述深度区间对各类声速剖面进行切割后,再分别利用各区间内的剖面数据进行EOF声速场建模。由于相邻深度区间声速模型所反演的声速剖面会在深度交界处出现数值错位的现象,为使各区间反演的分段声速剖面之间能平滑拼接,可在重叠区内利用上下两个区间反演的同一深度处的声速值进行加权平均,即式(10),进而组合成无缝的全海深声速剖面
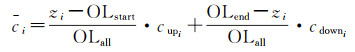 (10)
(10)
式中,OLall为相邻区间重叠区中的垂向空间跨度;OLstart和OLend分别为相邻区间重叠区顶部和底部的深度值;cupi为深度zi处利用上方声速模型反演的声速值;cdowni为深度zi处利用下方声速模型反演的声速值;ci为深度zi处加权平均后得到的声速值。
1.2 GNSS-声学位置增强服务的方法在没有声速信息的海域,可借鉴GNSS对流层误差的处理方法,即先将信号传播时间转换为距离,再借助高度角相关的投影函数、天顶对流层延迟的模型和参数对距离进行修正,进而支撑高精度位置服务。基于上述方法,本文利用海底大地控制点和海面浮标反演海域的声速改正信息支撑水下设备的高精度导航计算,即GNSS-声学位置增强服务。GNSS-声学海底定位的观测值是信号传播时间,为方便空间域的位置服务,首先用参考声速将观测的信号传播时间换算为距离L,再对L进行改正进而得到精确的几何距离,最后用精确的几何距离进行位置服务。其中,利用传播时间和参考声速反演声信号传播距离L(声程)的过程可表达为
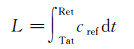 (11)
(11)
式中,cref为参考声速(本文取1500 m/s);Tat为信号发射时刻的标识;Ret为信号接收时刻的标识。由于时间微分dt与距离微分ds之间存在如下关系
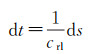 (12)
(12)
式中,crl为实际声速。
因此,式(11)可以改写为
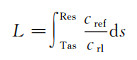 (13)
(13)
式中,Tas为信号发射处的位置标识;Res为信号接收处的位置标识。
进而,将声程L与直线几何距离G的互差表示为
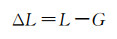 (14)
(14)
经过分离,上述互差可表示为声速误差和声线弯曲误差的综合影响
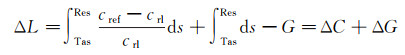 (15)
(15)
式中,ΔC表示声速误差;ΔG表示声线弯曲误差。
声线的初始入射角(声线在发射点处与铅垂线的夹角)不同时,声线弯曲的程度也不同,进而导致声线几何入射角(信号在发射点与接收点间的连线与铅垂线的夹角)相对初始入射角的偏差也不同,其所对应的海洋声速误差也不同。同时,为简化分析过程,本文将ΔC与ΔG统一为ΔL进行解算,不再分开讨论。此外,为了压缩声速误差改正数的数据量,便于产品的播发,进而实现水下设备的位置增强服务,本文利用声线几何入射角θgeo构建映射函数,再将同一时刻不同位置处海洋声速误差ΔL归算到垂直方向ΔL⊥。其中,在用户端加载功能类似超短基线系统的声学设备可直接对θgeo进行量测[75]。考虑到现有商业超短基线系统的测角精度一般优于0.3°,因此本文直接忽略了几何入射角测量误差的影响。此时,声速误差的垂向影响ΔL⊥,即垂向总距离差(nadir total range error, NTRE),可表示为
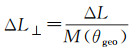 (16)
(16)
式中,M(θgeo)为与声线几何入射角θgeo相关的映射函数[20],可表示为
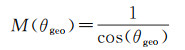 (17)
(17)
当声速剖面已知时,垂向总距离差可表示为
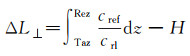 (18)
(18)
式中,Taz为信号发射处的垂向位置标识;Rez为信号接收处的垂向位置标识;H为信号发射点与信号接收点之间垂向距离的参考值,可由压力传感器直接测得。
为进行GNSS-声学导航定位服务,可基于海洋声速误差表达式(式(16))构建形如式(19)的观测方程。利用海底大地控制点和海面浮标组成服务端,解算垂向总距离差,并将该声速误差改正数作为产品播发给用户端,便可支撑用户利用海底大地控制点进行高精度的导航服务
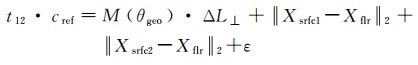 (19)
(19)
式中,t12为信号双程传播时间;cref为参考声速1500 m/s;Xsrfc1为信号发射时刻测船的位置;Xsrfc2为信号接收时刻测船的位置;Xflr为海底大地控制点位置;ε为观测误差。
1.3 海洋声速剖面层析方法由于利用浮标和海底大地控制点所解算的垂向总距离差ΔL⊥仅针对整个海洋水层,无法直接应用于水下航行器的位置服务,进而需对上述声速映射改正模型进行垂向分层,根据水下航行器的实际深度利用式(18)计算相应的声速改正数,以满足不同深度航行器的高精度导航解算。为此,对逐历元解算的垂向总距离差(NTRE)附加水平、垂直、先验等约束条件,进行海洋声速的层析,在无声速剖面实测数据的条件下构建类似1.1节的局部声速场模型。Munk深海声道轴模型[76](见式(20))是目前通用的声速剖面理论模型,被用作该部分研究工作的垂向约束条件。未来可直接从目标海区的大量实测声速剖面数据中提取声速垂向变化规律,并将其作为更准确的垂向约束条件辅助上述的声速层析工作
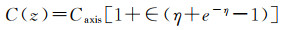 (20)
(20)
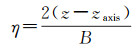 (21)
(21)
式中,z为深度;C(z)为深度z处的声速值;Caxis为声道轴处声速;∈为声速扰动系数;η为无量纲距离;zaxis为声道轴深度;B为声道尺度厚度。
对于局部海域,声速水平梯度的影响一般较小、可忽略,进而声速层析的目标可从声速场层析简化为各观测时刻声速剖面的求解。以每个历元计算的垂向总距离差ΔL⊥为观测值,采用Munk深海声道轴模型作为垂向约束,可构建积分形式的观测方程
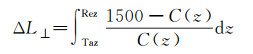 (22)
(22)
上述积分方程可离散化为
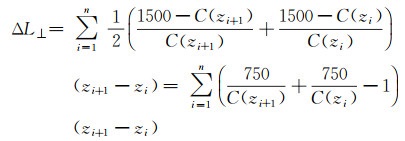 (23)
(23)
式中,n为声信号发射和接收深度区间分的层数;zi和zi+1分别为第i层上边界和下边界的深度。
为实时估算声速剖面,需解算Munk模型中的4个参数(声道轴处声速、声速的扰动系数、声道轴深度及声道尺度厚度),还要增加至少3个约束条件。考虑到深海声道轴深度较为稳定,可将其经验值设置为一个先验的约束条件
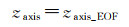 (24)
(24)
式中,zaxis_EOF为深海声道轴深度的先验值,本文直接从构建的EOF模型中提取。同时,海面声速、海底声速及潜航器处声速可分别由浮标、海底控制点及潜航器直接测量,也可将它们增设为约束条件
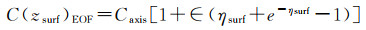 (25)
(25)
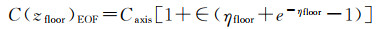 (26)
(26)
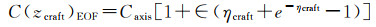 (27)
(27)
式中,zsurf、zfloor和zcraft分别为浮标、海底控制点及潜航器处的水深值。此时,联立式(23)—式(27)这5个观测方程,采用最小二乘法求解便可以得到各观测时刻的声速剖面参数。最后,潜航器可根据估算的剖面和实测的深度,利用式(18)分别求海面至潜航器及潜航器至海底的垂向总距离差,实现基于海底控制点的位置增强服务。
2 试验验证 2.1 试验与数据2019年7月14日至7月15日在南海的某海域进行了GNSS-声学定位试验,在海底一共布放了5个控制点,控制点间的距离约为2000 m。海面测船的航迹分为3类,包括围绕各控制点的半径约为1500 m的小圆轨迹,围绕5号控制点的半径约为4500 m的大圆轨迹,长度约6000 m、间隔约1000 m的14条线性航迹。期间共测量16组海洋参数剖面,包括10组XBT剖面、2组XCTD剖面及4组CTD剖面。上述数据的平面位置分布如图 1所示。
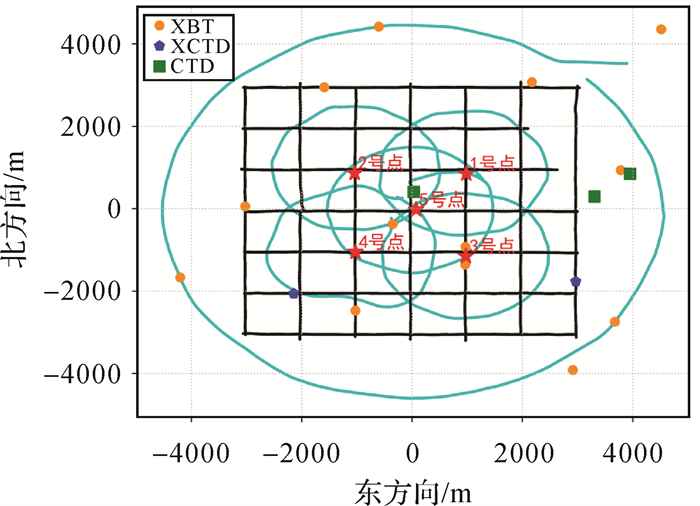
|
| 图 1 海底控制点、实测声速剖面以及海面测船航迹的分布 Fig. 1 Distribution of seafloor reference stations, measured sound speed profiles and the ship's track lines |
2.2 基于声速剖面时域变化分层模型确定海底大地控制点的位置
首先将实测的XBT剖面、XCTD剖面及CTD剖面全部反演成声速剖面,并将各剖面不同深度的声速值减去该深度的平均声速表征声速剖面的偏差,如图 2所示,蓝、黑和红分别对应XBT、XCTD和CTD剖面。由图 2可知,各声速剖面整体结构一致,声速由海洋表面的1545 m/s降至声道轴附近的1485 m/s,再升至海底1508 m/s;0~750 m的深度区间内,声速偏差可达4 m/s,主要集中在2 m/s以内;750~2000 m的深度区间内,声速偏差则主要集中在1 m/s以内;深度大于2000 m时,声速偏差小于1 dm/s。深海处声速的稳定性说明该垂向范围内海水介质的性质稳定,即环境受物理过程的扰动小。
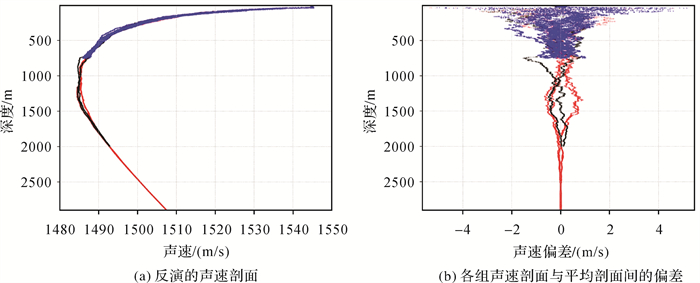
|
| 图 2 不同实测声速剖面的结构 Fig. 2 Structure of different measured sound speed profiles |
利用实测的16组声速剖面分层构建EOF声速剖面的时变模型,将上中下6层模型组合起来便得到试验海域的声速剖面时变模型(图 3)。由图 3可知,声速剖面的时域变化平稳,未展现出以天为周期的变化特征,这是由于EOF法采用式(7)和式(8)解算声速模型参数时对模态系数进行了线性拟合所致。为进一步说明所构建模型的可靠性,选取一条CTD剖面为验证剖面,将其与剩余剖面所构建的模型进行比对;再选一条参与建模的CTD剖面为验证剖面,将其与模型进行比对,结果如图 4所示。由图 4可知,水深500 m内验证剖面与模型之间的偏差主要集中在1 m/s内,水深大于500 m时,偏差则下降至分米/秒级别;相较于未参与建模的剖面,参与建模的剖面与模型间的偏差更加稳定,说明模型吸收了参与建模剖面的特征。上述结果明显优于各组声速剖面与平均剖面的偏差结果,说明了所构建的EOF声速模型的可靠性。

|
| 图 3 局部海洋声速剖面时变模型 Fig. 3 The time-varying model of local ocean sound speed profile |
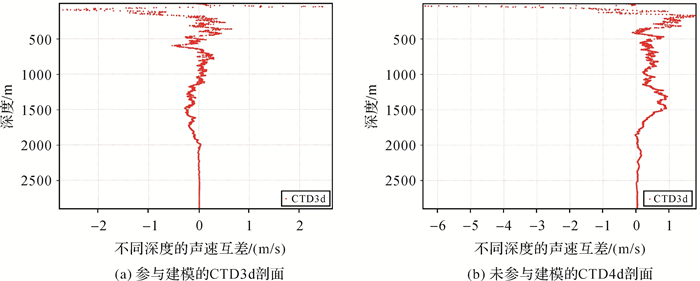
|
| 图 4 局部海洋声速剖面时变模型验证 Fig. 4 The time-varying model validation of local ocean sound speed profile |
为验证上述模型的效果,分别基于一条选定的声速剖面和EOF局部海洋声速剖面时变模型,利用不同航迹数据对海底的5号大地控制点进行定位。由于缺乏海底控制点坐标的真值,本文以不同航迹定位结果的均值为参考,检核不同航迹定位结果的精度。结果分别汇总至表 1和表 2。海试过程中,大圆航迹实施前后未进行声速剖面的测量。可以看出,基于EOF局部海洋声速剖面时变模型定位结果的各项指标优于基于单条声速剖面的定位结果,残差标准差和单位权中误差的最大值分别由1.546、1.125 m下降至0.895、0.633 m;与坐标均值的偏差也有明显的改善,尤其是高程方向的最大互差从1.512 m下降至0.513 m。上述结果说明基于声速剖面时变模型的定位结果具有较高有效性。
| 航迹和控制点编号 | 残差 | 单位权中误差 | 与坐标均值的偏差 | |||
| 均值 | 标准差 | N | E | H | ||
| 小圆 | 0.001 | 0.222 | 0.157 | -0.153 | -0.186 | -0.604 |
| 小圆加小十字 | 0.004 | 0.479 | 0.339 | -0.182 | -0.152 | -0.646 |
| 大圆 | 0.000 | 0.287 | 0.203 | 0.012 | 0.183 | 1.512 |
| 大圆加大十字 | 0.368 | 1.546 | 1.125 | 0.099 | 0.215 | 0.411 |
| 全部的线 | 0.004 | 0.965 | 0.683 | 0.222 | -0.061 | -0.675 |
| 航迹和控制点编号 | 残差 | 单位权中误差 | 与坐标均值的偏差 | |||
| 均值 | 标准差 | N | E | H | ||
| 小圆 | 0.000 | 0.207 | 0.147 | -0.090 | -0.165 | -0.172 |
| 小圆加小十字 | 0.004 | 0.252 | 0.178 | -0.086 | -0.126 | -0.228 |
| 大圆 | 0.000 | 0.346 | 0.245 | 0.081 | 0.326 | 0.513 |
| 大圆加大十字 | 0.134 | 0.635 | 0.460 | 0.105 | 0.327 | 0.090 |
| 全部的线 | 0.023 | 0.895 | 0.633 | -0.008 | -0.362 | -0.204 |
2.3 GNSS-声学位置增强服务
针对声速信息缺乏的情况,首先基于一条实测全海深声速剖面进行仿真试验,验证声速误差映射改正模型的有效性,再利用实测声学数据对映射改正模型的实际效果进行验证。仿真试验的条件如下:假设声信号自水深6 m处发射,几何入射角从0°~80°按1°间隔进行变化;同时假设信标深度从2500~3500 m按5 m间隔进行变化。采用声线跟踪算法确定不同几何入射角和信标深度条件下声信号传播时间,利用参考声速(1500 m/s)将声线跟踪的信号传播时间反演为距离,并将其与真实几何直线距离作差,得到海洋环境引起的延迟误差ΔL(图 5)。由图 5可知,海洋环境引起的延迟误差随几何入射角的增加而增大;但对相同的几何入射角,延迟误差随深度的增加反而减小。上述现象与声速垂向分布不均匀相关,也与参考声速数值选取相关。按式(18)计算不同深度条件下的垂向总距离差,再进一步按式(16)计算不同几何入射角条件下的映射改正值,并用其改正图 5所示的海洋环境延迟误差,得映射改正残差(图 6)。统计上述改正残差可知,几何入射角小于62°时,即水平距离小于1.7倍水深时,映射改正残差小于0.5 m。由于深海试验中水平距离一般不超过水深的1.5倍,故映射改正具有极高的实用性。
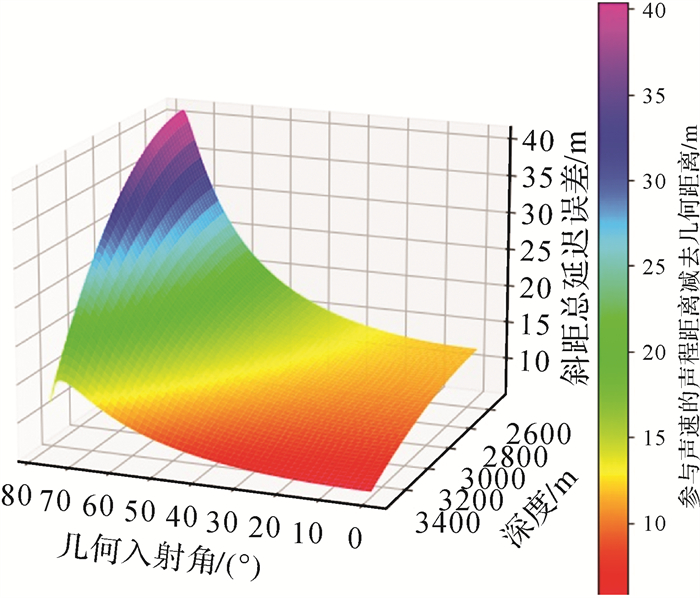
|
| 图 5 不同深度和几何入射角时海洋环境延迟误差 Fig. 5 Marine environment delay errors at different depths and geometric incidence angles |
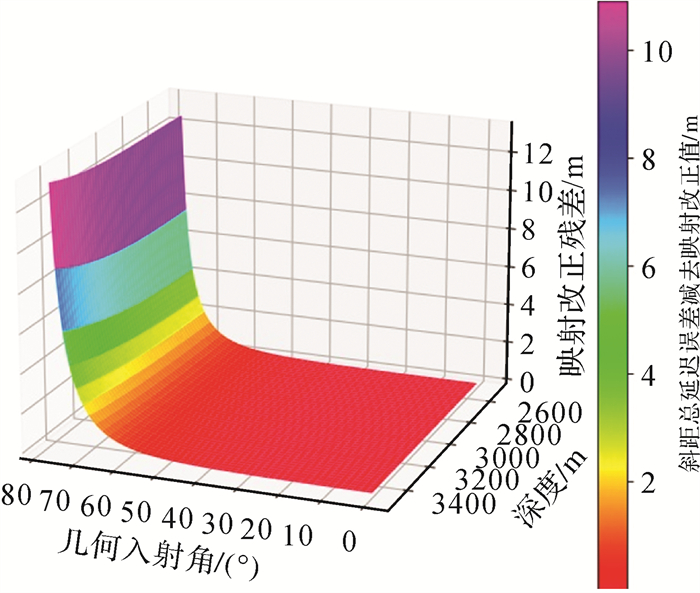
|
| 图 6 不同深度和几何入射角时映射改正的残差 Fig. 6 Mapping correction residuals for different depths and geometric incidence angles |
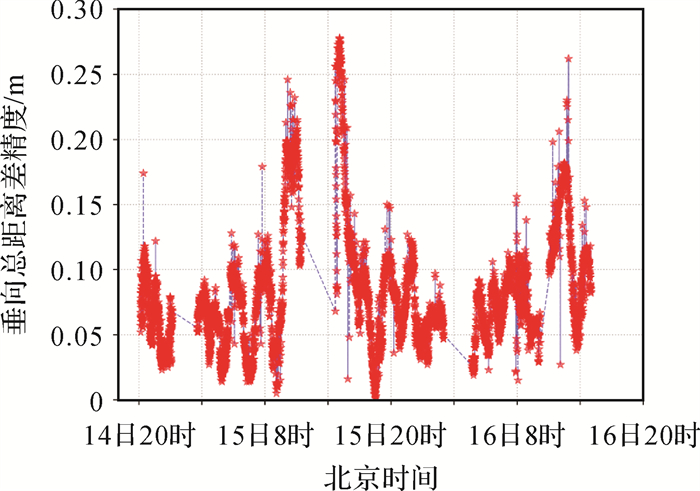
为验证声速误差映射改正模型在GNSS-声学位置增强服务中的实际效果,将图 1所示航迹的实测声学数据按等时间间隔抽稀为A、B两组数据。A组数据中认为测船的位置已知,构建观测方程式(19)。利用海底大地控制点位置Xflr、信号发射和接收时刻船载换能器的位置Xsrfc1和Xsrfc2、时延观测值t12、参考声速cref(本文取1500 m/s)及声线的几何入射角θgeo,采用序贯最小二乘平差法估算各观测时刻垂向总距离差ΔL⊥。输出ΔL⊥的时间序列如图 7所示,ΔL⊥中误差的时间序列如图 8所示。统计ΔL⊥与船载换能器所处位置大地高之间的相关性,可得相关系数为-0.107 1,说明两个物理量虽然负相关,但ΔL⊥变化的主因并非测船大地高的变化,而是声速时域变化。虽然ΔL⊥时域变化规律不明显,但不同年积日内有相似的结构:北京时间8时至20时可定义为大幅波动期,波动的幅度较大,可达1.5 m以上;北京时间20时至第2天8时可定义为波动平稳期,波动的幅度相对稳定,主要在0.5 m以内。其中,15日20时至16日00时的波动约为1 m,但仍然明显小于大幅波动期的幅度。上述波动的主要影响因素是海洋声速时域变化,此外参数的估计误差、船载换能器与海底应答器间相对位置变化导致的声线弯曲误差也是重要的影响因素。上述结果的主要波动趋势说明试验区海洋声速存在以天为周期的时域变化规律,与太阳运行规律有关。ΔL⊥中误差表现出与延迟误差相似的时域变化特征:波动平稳期中误差较为稳定,主要集中在0.1 m以内;大幅波动期的中误差则会出现明显波动,最大可达0.25 m。
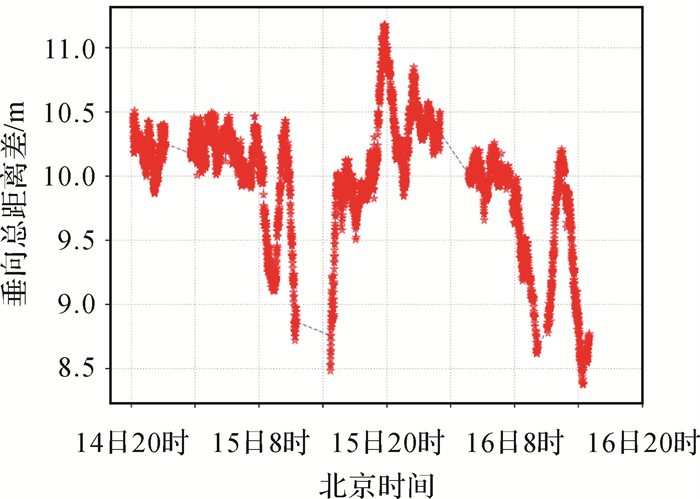
|
| 图 7 垂向总距离差的时序 Fig. 7 Time series of the total distance difference in the vertical direction |
|
| 图 8 垂向总距离差的中误差的时序 Fig. 8 Time series of the mean square error of total distance difference in the vertical direction |
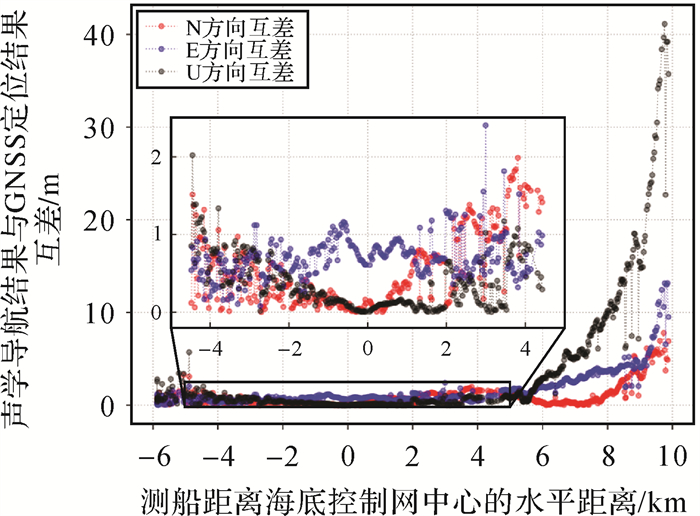
利用A组数据计算的垂向总距离差时间序列可内插得到B组数据中各时刻的垂向总距离差。试验中采用应答式工作模式,测船发射声信号后会历经不同时间以接收到来自不同控制点的反射信号。故同一历元不同观测值的观测方程中,信号发射时刻的测船位置一致时,信号接收时刻的测船位置则各不相同。为确保解算的可行,事先在每个历元内固定测船在信号发射时刻与信号接收时刻间的相对位置,即模拟附加了惯性导航数据的场景。最终,解算测船在信号发射时刻的三维位置及其精度,计算逐历元定位结果精度的均值,并统计声学导航结果与GNSS定位结果互差的RMS,将上述指标汇总于表 3。可以看出,海底控制网中心水平距离3000 m范围内导航结果精度均为分米级;剔除粗差数据后1号小圆的导航结果精度最优(厘米级);线性走航的导航结果精度相对较差(0.8~0.9 m);大圆距控制网中心4500 m,其导航精度最差(水平方向约为2 m,垂直方向约为3 m)。与GNSS定位结果进行对比可发现,海底控制点导航结果具有较高精度,距控制网中心3000 m范围内的导航结果偏差均为分米级,距控制网中心4500 m处导航结果偏差则为米级(1~2 m)。为进一步验证映射改正的实际效果,本文利用上述改正方法对试验中一条在海面横穿海底控制网的导航线数据(长约16 000 m)进行导航定位处理,输出声学导航结果与GNSS定位结果的互差(图 9)。由图 9可以看出,随着测船距海底控制网中心水平距离的增加,声学导航三维结果的精度在水平距离6000 m范围内逐渐变大(水平距离3000 m范围内精度主要为分米级,水平距离4500 m处精度主要为1~2 m),而水平距离6000 m范围外则迅速增加,在10 000 m处水平方向结果精度约为10 m、垂直方向结果精度大于40 m。上述结果验证了声速映射改正模型的有效性,创新了水下位置增强服务的工程应用方法。同时,结果也说明映射改正的精度与声线几何入射角大小呈负相关,该结论与仿真结果一致。文献[50]推导的定位误差模型表明:随着几何入射角的增大,声线跟踪误差对定位结果的影响明显增大。因此,推测本文的映射改正误差与声线的弯曲误差相关,需在后续的工作中进一步研究优化映射改正模型的方法。
| 航迹名称 (时序排列) |
逐历元精度的均值 | 与GNSS互差的RMS | |||||
| N方向 | E方向 | U方向 | N方向 | E方向 | U方向 | ||
| 小圆_1号点 | 0.098 | 0.096 | 0.052 | 0.635 | 0.297 | 0.225 | |
| 小圆_2号点 | 0.278 | 0.267 | 0.192 | 0.579 | 0.438 | 0.420 | |
| 小圆_4号点 | 0.523 | 0.509 | 0.356 | 0.534 | 0.532 | 0.379 | |
| 小圆_3号点 | 0.299 | 0.292 | 0.191 | 0.482 | 0.333 | 0.237 | |
| 线型走航 | 0.865 | 0.841 | 0.917 | 0.831 | 1.295 | 0.790 | |
| 小圆_5号点 | 0.378 | 0.367 | 0.196 | 0.519 | 0.343 | 0.200 | |
| 大圆 | 2.021 | 1.983 | 2.890 | 1.092 | 1.944 | 1.503 | |
|
| 图 9 声学导航结果精度随测船位置的变化 Fig. 9 Accuracy of acoustic navigation results varying with ship position |
2.4 海洋声速剖面的层析
为了验证本文提出的海洋声速剖面层析方法,支撑水下潜航器位置服务,提取图 1中5号控制点上方小圆轨迹的观测数据,将测船当作浮标并分别假设潜航器位于水深500 m和1500 m处,进行声速层析仿真试验。对于每一个观测历元,以同期估算的垂向总距离差为观测值,从构建的EOF声速剖面的时变模型中分别提取船载换能器深度、海底控制点深度及潜航器深度处的声速值作为先验约束,并用Munk模型作为声速廓线的垂向约束,对式(23)—式(27)进行线性化处理,构建观测方程组式(28)
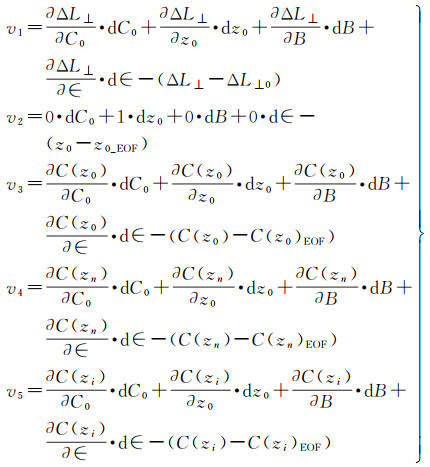 (28)
(28)
式中,dC0、dz0、dB和dε分别代表声道轴处声速、声速扰动系数、声道轴深度及声道尺度厚度这4个待求参数的改正数,它们的系数为相应观测值的一阶偏微分;ΔL⊥、z0、C(z0)、C(zn)和C(zi)分别代表垂向总距离差观测值、深海声道轴深度观测值、海面声速观测值、海底声速观测值及潜航器处声速观测值;ΔL⊥0、z0_EOF、C(z0)EOF、C(zn)EOF和C(zi)EOF为声道轴处声速、声速扰动系数、声道轴深度及声道尺度厚度这4个参数取初值时上述观测值所对应的计算值;v1、v2、v3、v4和v5则分别代表上述观测值与计算值互差的残差。
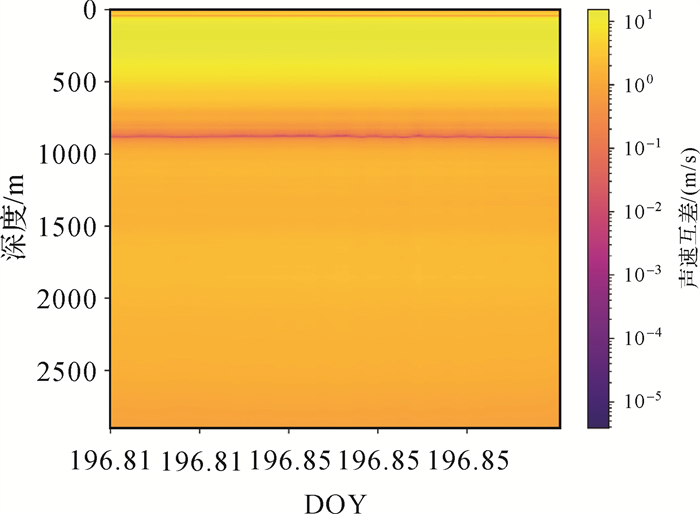
最后基于等权随机模型,逐历元估算声速剖面的声道轴处声速、声速扰动系数、声道轴深度及声道尺度厚度等4个必要参数,构成时间域的局部声速剖面模型,并将估算的声速模型与构建的EOF声速剖面时变模型进行对比,可得图 10和图 11。可以看出,等温层(深度大于1000 m)反演声速精度明显优于温跃层(深度小于1000 m)反演声速精度。统计图中的数据见表 4,当潜航器深度为500 m时,估算声速精度最高的深度位于659 m;深度大于500 m的区间,估算声速剖面与本文构建的EOF声速剖面时变模型间互差的RMS约为3.39 m/s;当深度小于500 m时,上述互差值的RMS约为10.24 m/s。当潜航器深度为1500 m时,估算声速精度最高的深度位于881 m;当深度大于1500 m时,估算声速剖面与本文构建的EOF声速剖面时变模型间互差的RMS约为1.67 m/s;当深度小于1500 m时,上述互差的RMS约为6.61 m/s。上述误差主要由垂向总距离差的估算精度及Munk模型的代表性误差综合导致,结果表明:在深海区域,潜航器越深,反演声速剖面的精度越高,进而用其进行导航定位服务的精度也越高;其中浅层海域声速变化不规律,需更多的约束条件进行浅层区间声速的高精度反演,以支撑该深度区间内潜航器的导航位置服务。

|
| 图 10 潜航器深度为500 m时逐历元反演声速剖面的精度 Fig. 10 Accuracy of sound speed profile inversed when the submarine is at depth of 500 m |
|
| 图 11 潜航器深度为1500 m时逐历元反演声速剖面的精度 Fig. 11 Accuracy of sound speed profile inversed when the submarine is at depth of 1500 m |
| 潜航器深度/m | 反演声速精度最高的深度/m | 深度小于潜航器深度的区间内声速精度/(m/s) | 深度大于潜航器深度的区间内声速精度/(m/s) |
| 500 | 659 | 10.23 | 3.39 |
| 1500 | 881 | 6.61 | 1.67 |
3 结语
目前,GNSS-声学定位是用于海底大地测量的热门技术,但它还不能直接应用于水下的位置服务。为此,本文针对水下位置服务这一需求,研究了局域声速剖面时变模型的构建及应用,创新了声速信息缺乏条件下的GNSS-声学位置增强服务方法及海洋声速剖面的层析方法。
最后,用南海3000 m水深海域的实测数据对本文方法进行了验证,结果表明:
(1) 相对于单条声速剖面,构建的声速剖面时变模型可明显改善定位结果的指标,将控制点位置的精度控制在分米级以内。
(2) 声线几何入射角小于62°时,即水平距离小于1.7倍水深时,提出的空间域映射改正的残差小于0.5 m;基于该映射改正模型,可为距控制网中心水平距离3000 m范围内测船提供分米级精度的逐历元位置服务。
(3) 针对水下潜航器位置服务提出的基于Munk深海声道轴模型的海洋声速剖面时变模型层析方法,可通过附加约束条件的方式逐历元地估算声速剖面,使深度大于潜航器的区间内声速精度优于3.5 m/s。
| [1] |
汪品先. 深海浅说[M]. 上海: 上海科技教育出版社, 2020. WANG Pinxian. A brief introduction to the deep sea[M]. Shanghai: Shanghai Science and Technology Education Press, 2020. |
| [2] |
刘经南, 陈冠旭, 赵建虎, 等. 海洋时空基准网的进展与趋势[J]. 武汉大学学报(信息科学版), 2019, 44(1): 17-37. LIU Jingnan, CHEN Guanxu, ZHAO Jianhu, et al. Development and trends of marine space-time frame network[J]. Geomatics and Information Science of Wuhan University, 2019, 44(1): 17-37. |
| [3] |
刘经南. 全球性海洋时空基准与环境监测网构建的若干思考[R]. 杭州: 国家海洋局第二海洋研究所, 2015. LIU Jingnan. Some thoughts on the construction of a global marine space-time frame and environmental monitoring network[R]. Hangzhou: The Second Institute of Oceanography, State Oceanic Administration, 2015. |
| [4] |
杨元喜, 徐天河, 薛树强. 我国海洋大地测量基准与海洋导航技术研究进展与展望[J]. 测绘学报, 2017, 46(1): 1-8. YANG Yuanxi, XU Tianhe, XUE Shuqiang. Progresses and prospects in developing marine geodetic datum and marine navigation of China[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(1): 1-8. DOI:10.11947/j.AGCS.2017.20160519 |
| [5] |
YANG Yuanxi, XU Tianhe, XUE Shuqiang. Progresses and prospects of marine geodetic datum and marine navigation in China[J]. Journal of Geodesy and Geoinformation Science, 2018, 1(1): 16-24. |
| [6] |
杨元喜, 刘焱雄, 孙大军, 等. 海底大地基准网建设及其关键技术[J]. 中国科学: 地球科学, 2020, 50(7): 936-945. YANG Yuanxi, LIU Yanxiong, SUN Dajun, et al. Seafloor geodetic network establishment and key technologies[J]. China Science: Earth Science, 2020, 50(7): 936-945. |
| [7] |
YANG Yuanxi, LIU Yanxiong, SUN Dajun, et al. Seafloor geodetic network establishment and key technologies[J]. Science China Earth Sciences, 2020, 63(8): 1188-1198. DOI:10.1007/s11430-019-9602-3 |
| [8] |
李林阳, 吕志平, 崔阳. 海底大地测量控制网研究进展综述[J]. 测绘通报, 2018(1): 8-13. LI Linyang, LV Zhiping, CUI Yang. Summary of the research progress of seafloor geodetic control network[J]. Bulletin of Surveying and Mapping, 2018(1): 8-13. |
| [9] |
孙大军, 郑翠娥, 张居成, 等. 水声定位导航技术的发展与展望[J]. 中国科学院院刊, 2019, 34(3): 331-338. SUN Dajun, ZHENG Cuie, ZHANG Jucheng, et al. Development and prospect for underwater acoustic positioning and navigation technology[J]. Bulletin of Chinese Academy of Sciences, 2019, 34(3): 331-338. |
| [10] |
CHADWELL CD, SPIESS FN, HILDEBRAND JA, et al. Sea floor strain measurement using GPS and acoustics[M]. Berlin, Heidelberg: Springer, 1997: 682-689.
|
| [11] |
CHADWELL CD. Shipboard towers for global positioning system antennas[J]. Ocean Engineering, 2003, 30(12): 1467-1487. DOI:10.1016/S0029-8018(02)00141-5 |
| [12] |
ASADA A, YABUKI T. Centimeter-level positioning on the seafloor[J]. Proceedings of the Japan Academy, 2001, 77(1): 7-12. DOI:10.2183/pjab.77.7 |
| [13] |
FUJIMOTO H, KIDO M, OSADA Y, et al. Long-term stability of acoustic benchmarks deployed on thick sediment for GPS/acoustic seafloor positioning[M]. Dordrecht: Springer, 2011: 263-272.
|
| [14] |
NISHIMURA T, SATO M, SAGIYA T. Global positioning system (GPS) and GPS-acoustic observations: Insight into slip along the subduction zones around Japan[J]. Annual Review of Earth and Planetary Sciences, 2014, 42: 653-674. DOI:10.1146/annurev-earth-060313-054614 |
| [15] |
ISHIKAWA T, YOKOTA Y, WATANABE S, et al. History of on-board equipment improvement for GNSS-A observation with focus on observation frequency[J]. Frontiers in Earth Science, 2020, 8: 150. DOI:10.3389/feart.2020.00150 |
| [16] |
KIDO M, FUJIMOTO H, HINO R, et al. Progress in the project for development of GPS/acoustic technique over the last 4 years[C]//Proceedings of 2014 International Symposium on Geodesy for Earthquake and Natural Hazards. International symposium on geodesy for earthquake and natural hazards (GENAH). Matsushima, Japan: Springer, 2014: 3-10.
|
| [17] |
SPIESS F N, CHADWELL C D, HILDEBRAND J A, et al. Precise GPS/acoustic positioning of seafloor reference points for tectonic studies[J]. Physics of the Earth and Planetary Interiors, 1998, 108(2): 101-112. DOI:10.1016/S0031-9201(98)00089-2 |
| [18] |
CHADWELL C D, SPIESS F N. Plate motion at the ridge- transform boundary of the south cleft segment of the Juan de Fuca Ridge from GPS-acoustic data[J]. Journal of Geophysical Research: Solid Earth, 2008, 113. DOI:10.1029/2007JB004936 |
| [19] |
HONSHO C, KIDO M. Comprehensive analysis of traveltime data collected through GPS-acoustic observation of seafloor crustal movements[J]. Journal of Geophysical Research: Solid Earth, 2017, 122(10): 8583-8599. DOI:10.1002/2017JB014733 |
| [20] |
HONSHO C, KIDO M, TOMITA F, et al. Offshore postseismic deformation of the 2011 Tohoku earthquake revisited: application of an improved GPS-acoustic positioning method considering horizontal gradient of sound speed structure[J]. Journal of Geophysical Research: Solid Earth, 2019, 124(6): 5990-6009. DOI:10.1029/2018JB017135 |
| [21] |
SATO M, FUJITA M, MATSUMOTO Y, et al. Improvement of GPS/acoustic seafloor positioning precision through controlling the ship's track line[J]. Journal of Geodesy, 2013, 87(9): 825-842. DOI:10.1007/s00190-013-0649-9 |
| [22] |
TADOKORO K, ANDO M, IKUTA R, et al. Observation of coseismic seafloor crustal deformation due to M7 class offshore earthquakes[J]. Geophysical Research Letters, 2006, 33(23): 23306-1. DOI:10.1029/2006GL026742 |
| [23] |
IKUTA R, TADOKORO K, ANDO M, et al. A new GPS- acoustic method for measuring ocean floor crustal deformation: application to the Nankai Trough[J]. Journal of Geophysical Research: Solid Earth, 2008, 113: B02401. DOI:10.1029/2006JB004875 |
| [24] |
YOKOTA Y, ISHIKAWA T, WATANABE S, et al. Seafloor geodetic constraints on interplate coupling of the Nankai Trough megathrust zone[J]. Nature, 2016, 534(7607): 374-377. DOI:10.1038/nature17632 |
| [25] |
SATO M, ISHIKAWA T, UJIHARA N, et al. Displacement above the hypocenter of the 2011 Tohoku-Oki earthquake[J]. Science, 2011, 332(6036): 1395. DOI:10.1126/science.1207401 |
| [26] |
CHEN G, LIU Y, LIU Y, et al. Improving GNSS-acoustic positioning by optimizing the ship's track lines and observation combinations[J]. Journal of Geodesy, 2020, 94(6): 1-14. |
| [27] |
刘伯胜, 雷家煜. 水声学原理[M]. 哈尔滨: 哈尔滨工程大学出版社, 2010. LIU Bosheng, LEI Jiayu. The principle of hydroacoustics[M]. Harbin: Harbin Engineering University Press, 2010. |
| [28] |
汪德昭, 尚尔昌. 水声学[M]. 2版. 北京: 科学出版社, 2013. WANG Dezhao, SHANG Erchang. Hydroacoustics[M]. 2nd ed. Beijing: Science Press, 2013. |
| [29] |
KIDO M, FUJIMOTO H, MIURA S, et al. Seafloor displacement at Kumano-nada caused by the 2004 off Kii Peninsula earthquakes, detected through repeated GPS/acoustic surveys[J]. Earth, planets and space, 2006, 58(7): 911-915. DOI:10.1186/BF03351996 |
| [30] |
MATSUI R, KIDO M, NIWA Y, et al. Effects of disturbance of seawater excited by internal wave on GNSS-acoustic positioning[J]. Marine Geophysical Research, 2019, 40: 541-555. DOI:10.1007/s11001-019-09394-6 |
| [31] |
赵建虎, 梁文彪. 海底控制网测量和解算中的几个关键问题[J]. 测绘学报, 2019, 48(9): 1197-1202. ZHAO Jianhu, LIANG Wenbiao. Some key points of submarine control network measurement and calculation[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(9): 1197-1202. DOI:10.11947/j.AGCS.2019.20190157 |
| [32] |
HJELMERVIK K T, HJELMERVIK K. Improved estimation of oceanographic climatology using empirical orthogonal functions and clustering[C]//Proceedings of 2013 MTS/IEEE OCEANS-Bergen. Bergen, Norway: IEEE, 2013: 1-5.
|
| [33] |
吴永亭. LBL精密定位理论方法研究及软件系统研制[D]. 武汉: 武汉大学, 2013. WU Yongting. Study on theory and method of precise LBL positioning and development of positioning software system[D]. Wuhan: Wuhan University, 2013. |
| [34] |
孙文舟, 殷晓冬, 暴景阳, 等. 声速剖面EOF表示的第一模态解析[J]. 海洋测绘, 2019, 39(3): 31-35. SUN Wenzhou, YIN Xiaodong, BAO Jingyang, et al. The first model analysis of sound speed profile represented by EOF[J]. Hydrographic Surveying and Charting, 2019, 39(3): 31-35. |
| [35] |
ISHIKAWA T, FUJITA M. Inverse method and precision improvement for seafloor positioning[J]. Journal of the Oceanographical Society of Japan, 2005, 41: 27-34. |
| [36] |
FUJITA M, ISHIKAWA T, MOCHIZUKI M, et al. GPS/ acoustic seafloor geodetic observation: method of data analysis and its application[J]. Earth, Planets and Space, 2006, 58(3): 265-275. DOI:10.1186/BF03351923 |
| [37] |
YANG Yuanxi, QIN Xianping. Resilient observation models for seafloor geodetic positioning[J]. Journal of Geodesy, 2021, 95(7): 79. DOI:10.1007/s00190-021-01531-7 |
| [38] |
YASUDA K, TADOKORO K, TANIGUCHI S, et al. Interplate locking condition derived from seafloor geodetic observation in the shallowest subduction segment at the central Nankai Trough, Japan[J]. Geophysical Research Letters, 2017, 44(8): 3572-3579. DOI:10.1002/2017GL072918 |
| [39] |
WATANABE S I, ISHIKAWA T, YOKOTA Y, et al. GARPOS: analysis software for the GNSS-a seafloor positioning with simultaneous estimation of sound speed structure[J]. Frontiers in Earth Science, 2020, 8: 597532. DOI:10.3389/feart.2020.597532 |
| [40] |
TOMITA F, KIDO M, HONSHO C, et al. Development of a kinematic GNSS-acoustic positioning method based on a state-space model[J]. Earth, Planets and Space, 2019, 71(1): 1-24. DOI:10.1186/s40623-018-0980-8 |
| [41] |
YOKOTA Y, ISHIKAWA T, WATANABE S I. Gradient field of undersea sound speed structure extracted from the GNSS-A oceanography[J]. Marine Geophysical Research, 2019, 40(4): 493-504. DOI:10.1007/s11001-018-9362-7 |
| [42] |
YOKOTA Y, ISHIKAWA T. Gradient field of undersea sound speed structure extracted from the GNSS-A oceanography: GNSS-A as a sensor for detecting sound speed gradient[J]. SN Applied Sciences, 2019, 1(7): 1-11. |
| [43] |
YOKOTA Y, ISHIKAWA T, WATANABE S I, et al. Kilometer-scale sound speed structure that affects GNSS-a observation: case study off the kii channel[J]. Frontiers in Earth Science, 2020, 8: 331. DOI:10.3389/feart.2020.00331 |
| [44] |
ZHAO S, WANG Z, HE K, et al. Investigation on underwater positioning stochastic model based on acoustic ray incidence angle[J]. Applied Ocean Research, 2018, 77: 69-77. DOI:10.1016/j.apor.2018.05.011 |
| [45] |
WANG Z, ZHAO S, JI S, et al. Real-time stochastic model for precise underwater positioning[J]. Applied Acoustics, 2019, 150: 36-43. DOI:10.1016/j.apacoust.2019.01.021 |
| [46] |
LIU Y, XUE S, QU G, et al. Influence of the ray elevation angle on seafloor positioning precision in the context of acoustic ray tracing algorithm[J]. Applied Ocean Research, 2020, 105: 102403. DOI:10.1016/j.apor.2020.102403 |
| [47] |
王薪普, 薛树强, 曲国庆, 等. 水下定位声线扰动分析与分段指数权函数设计[J]. 测绘学报, 2021, 50(7): 982-989. WANG Xinpu, XUE Shuqiang, QU Guoqing, et al. Disturbance analysis of underwater positioning acoustic ray and design of piecewise exponential weight function[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(7): 982-989. DOI:10.11947/j.AGCS.2021.20200424 |
| [48] |
马越原, 曾安敏, 许扬胤, 等. 声线入射角随机模型在深海环境中的应用[J]. 导航定位学报, 2020, 8(3): 65-68. MA Yueyuan, ZENG Anmin, XU Yangyin, et al. Application of incidence angle stochastic model of acoustic lines under deep sea environment[J]. Journal of Navigation and Positioning, 2020, 8(3): 65-68. |
| [49] |
郑根, 张红梅, 冯磊, 等. 基于面积差的声速剖面自适应简化方法[J]. 测绘学报, 2018, 47(10): 1415-1423. ZHENG Gen, ZHANG Hongmei, FENG Lei, et al. An adaptive simplification method of SVP based on area difference[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(10): 1415-1423. DOI:10.11947/j.AGCS.2018.20170232 |
| [50] |
CHEN X, ZHANG H, ZHAO J, et al. Positioning accuracy model of sailing-circle GPS-acoustic method[J]. Earth and Space Science, 2021, e2019EA000639. |
| [51] |
王振杰, 李圣雪, 聂志喜, 等. 水声定位中一种大入射角声线跟踪方法[J]. 武汉大学学报(信息科学版), 2016, 41(10): 1404-1408. WANG Zhenjie, LI Shengxue, NIE Zhixi, et al. A large incidence angle ray-tracing method for underwater acoustic positioning[J]. Geomatics and Information Science of Wuhan University, 2016, 41(10): 1404-1408. |
| [52] |
闫凤池, 王振杰, 赵爽, 等. 顾及双程声径的常梯度声线跟踪水下定位算法[J]. 测绘学报, 2022, 51(1): 31-40. YAN Fengchi, WANG Zhenjie, ZHAO Shuang, et al. A layered constant gradient acoustic ray tracing underwater positioning algorithm considering round-trip acoustic path[J]. Acta Geodaetica et Cartographica Sinica, 2022, 51(1): 31-40. DOI:10.11947/j.AGCS.2022.20210234 |
| [53] |
YANG Wenlong, XUE Shugiang, LIU Yixu. P-order secant method for rapidly solving the ray inverse problem of underwater acoustic positioning[J]. Marine Geodesy, 2021, 44(1): 3-15. |
| [54] |
SUN D, LI H, ZHENG C, et al. Sound velocity correction based on effective sound velocity for underwater acoustic positioning systems[J]. Applied Acoustics, 2019, 151: 55-62. DOI:10.1016/j.apacoust.2019.02.027 |
| [55] |
赵建虎, 张红梅, 吴猛. 一种基于常梯度模板插值的声线跟踪算法[J]. 武汉大学学报(信息科学版), 2021, 46(1): 71-78. ZHAO Jianhu, ZHANG Hongmei, WU Meng. A sound ray tracking algorithm based on template-interpolation of constant-gradient sound velocity[J]. Geomatics and Information Science of Wuhan University, 2021, 46(1): 71-78. |
| [56] |
LIU Yixu, LU Xiushan, XUE Shuqiang, et al. A new underwater positioning model based on average sound speed[J]. Journal of Navigation, 2021, 74(5): 1009-1025. DOI:10.1017/S0373463321000400 |
| [57] |
YANG Fanlin, LU Xiushan, LI Jiabiao, et al. Precise positioning of underwater static objects without sound speed profile[J]. Marine Geodesy, 2011, 34(2): 138-151. DOI:10.1080/01490419.2010.518501 |
| [58] |
XIN Mingzhen, YANG Fanlin, WANG Faxing, et al. A TOA/AOA underwater acoustic positioning system based on the equivalent sound speed[J]. Journal of Navigation, 2018, 71(6): 1431-1440. |
| [59] |
赵建虎. 一种无需声速测量的水下高精度导航定位方法[R]. 青岛: 第四届中国大地测量和地球物理学学术大会, 2021. ZHAO Jianhu. An underwater high-precision navigation and positioning method without sound speed measurements[R]. Qingdao: The 4th Chinese Geodesy and Geophysics Conference, 2021. |
| [60] |
邝英才, 吕志平, 王方超, 等. GNSS/声学联合定位的自适应滤波算法[J]. 测绘学报, 2020, 49(7): 854-864. KUANG Yingcai, LV Zhiping, WANG Fangchao, et al. The adaptive filtering algorithm of GNSS/acoustic joint positioning[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(7): 854-864. DOI:10.11947/j.AGCS.2020.20190393 |
| [61] |
KUANG Y, LV Z, LI L, et al. Robust constrained Kalman filter algorithm considering time registration for GNSS/acoustic joint positioning[J]. Applied Ocean Research, 2021, 107: 102435. |
| [62] |
KUANG Y, LV Z, WANG J, et al. The GNSS/acoustic one-step positioning model with attitude parameters[C]//Proceedings of the 10th China Satellite Navigation Conference (CSNC). Beijing, China: Springer. 2019.
|
| [63] |
WANG J, XU T, LIU Y, et al. Kalman filter based acoustic positioning of deep seafloor datum point with two-step systematic error estimation[J]. Applied Ocean Research, 2021, 114: 102817. |
| [64] |
WANG J, XU T, ZHANG B, et al. Underwater acoustic positioning based on the robust zero-difference Kalman filter[J]. Journal of Marine Science and Technology, 2021, 26: 734-749. |
| [65] |
CHEN G, LIU Y, LIU Y, et al. Adjustment of transceiver lever arm offset and sound speed bias for GNSS-acoustic positioning[J]. Remote Sensing, 2019, 11(13): 1606. |
| [66] |
刘焱雄, 彭琳, 吴永亭, 等. 超短基线水声定位系统校准方法研究[J]. 武汉大学学报(信息科学版), 2006, 31(7): 610-612. LIU Yanxiong, PENG Lin, WU Yongting, et al. Calibration of transducer and transponder positions[J]. Geomatics and Information Science of Wuhan University, 2006, 31(7): 610-612. |
| [67] |
LIU H, WANG Z, ZHAO S, et al. Accurate multiple ocean bottom seismometer positioning in shallow water using GNSS/acoustic technique[J]. Sensors, 2019, 19(6): 1406. |
| [68] |
ZHAO S, WANG Z, NIE Z, et al. Investigation on total adjustment of the transducer and seafloor transponder for GNSS/acoustic precise underwater point positioning[J]. Ocean Engineering, 2021, 221: 108533. |
| [69] |
XU P, ANDO M, TADOKORO K. Precise, three-dimensional seafloor geodetic deformation measurements using difference techniques[J]. Earth, Planets and Space, 2005, 57(9): 795-808. |
| [70] |
王毅. 石油勘探中水下高精度定位算法研究[D]. 青岛: 中国石油大学(华东), 2014. WANG Yi. Research on algorithms of high-precision underwater positioning in petroleum exploration[D]. Qingdao: China University of Petroleum, 2014. |
| [71] |
ZHAO S, WANG Z, HE K, et al. Investigation on stochastic model refinement for precise underwater positioning[J]. IEEE Journal of Oceanic Engineering, 2019, 45(4): 1482-1496. |
| [72] |
曾安敏, 杨元喜, 明锋, 等. 海底大地基准点圆走航模式定位模型及分析[J]. 测绘学报, 2021, 50(7): 939-952. ZENG Anmin, YANG Yuanxi, MING Feng, et al. Positioning model and analysis of the sailing circle mode of seafloor geodetic datum points[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(7): 939-952. DOI:10.11947/j.AGCS.2021.20200529 |
| [73] |
XUE S, YANG Y, YANG W. Single-differenced models for GNSS-acoustic seafloor point positioning[J]. Journal of Geodesy, 2022, 96(5): 1-22. |
| [74] |
张旭, 张永刚, 张健雪, 等. 一种新的声速剖面结构参数化方法[J]. 海洋学报, 2011, 33(5): 54-60. ZHANG Xu, ZHANG Yonggang, ZHANG Jianxue, et al. A new model for calculating sound speed profile structure[J]. Acta Oceanologica Sinica, 2011, 33(5): 54-60. |
| [75] |
SAKIC P, CHUPIN C, BALLU V, et al. Geodetic seafloor positioning using an unmanned surface vehicle-contribution of direction-of-arrival observations[J]. Frontiers in Earth Science, 2021, 9: 636156. |
| [76] |
MUNK W H. Sound channel in an exponentially stratified ocean, with application to SOFAR[J]. The Journal of the Acoustical Society of America, 1974, 55(2): 220-226. |



