



Acta Geodaetica et Cartographica Sinica ›› 2024, Vol. 53 ›› Issue (11): 2178-2188.doi: 10.11947/j.AGCS.2024.20240027
• Geodesy and Navigation • Previous Articles
Chuan HU( ), Zonghao SHI, Daqin REN
), Zonghao SHI, Daqin REN
Received:2024-01-06
Published:2024-12-13
About author:HU Chuan (1983—), male, PhD, associate professor, majors in the theory and methods of measurement data processing. E-mail: hucch@cqjtu.edu.cn
Supported by:CLC Number:
Chuan HU, Zonghao SHI, Daqin REN. On homotopy method to parameter estimation for generalized nonlinear Gauss-Helmert model[J]. Acta Geodaetica et Cartographica Sinica, 2024, 53(11): 2178-2188.
Tab.3
The results of general homotopy adjustment (example 2)"
| 参数项 | 采用初值1 | 采用初值2 | ||
|---|---|---|---|---|
| 高斯-牛顿法 | 通用同伦平差法 | 高斯-牛顿法 | 通用同伦平差法 | |
| Xu/m | -2 157 555.665 | -2 157 555.665 | ||
| Yu/m | 4 380 372.532 | 4 380 372.532 | ||
| Zu/m | 4 081 041.770 | 4 081 041.770 | ||
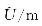 | 175 322.286 | 175 322.286 | ||
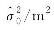 | 不收敛 | 137 879 264.216 | 不收敛 | 137 879 264.215 |
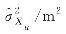 | 293 314 174.167 | 293 314 174.167 | ||
 | 336 342 488.338 | 336 342 488.338 | ||
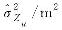 | 266 625 946.277 | 266 625 946.277 | ||
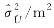 | 240 957 927.393 | 240 957 927.393 | ||
Tab.7
Adjustment results (example 4)"
| 坐标 | 采用初值1 | 采用初值2 | ||
|---|---|---|---|---|
| 高斯-牛顿法 | 通用同伦平差法 | 高斯-牛顿法 | 通用同伦平差法 | |
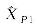 | 9 034.167 03 | 9 034.167 03 | 8 551.905 79 | |
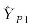 | 907.528 22 | 907.528 22 | 534.879 53 | |
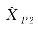 | 8 762.945 47 | 8 762.945 47 | 8 410.402 64 | |
 | 1 124.473 48 | 1 124.473 48 | 发散 | 852.059 65 |
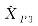 | 9 221.056 88 | 9 221.056 88 | 8 407.059 58 | |
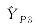 | 1 008.491 04 | 1 008.491 04 | 379.506 16 | |
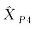 | 9 031.113 45 | 9 031.113 45 | 8 129.022 37 | |
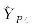 | 1 345.343 85 | 1 345.343 85 | 648.287 90 | |
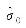 | 0.001 87 | 0.001 87 | 0.001 87 | |
| [1] | HU Yu, FANG Xing. Linear estimation under the Gauss-Helmert model: geometrical interpretation and general solution[J]. Journal of Geodesy, 2023, 97(5): 44. |
| [2] | NEITZEL F. Generalization of total least-squares on example of unweighted and weighted 2D similarity transformation[J]. Journal of Geodesy, 2010, 84(12): 751-762. |
| [3] | KANATANI K, NIITSUMA H. Optimal computation of 3D similarity: Gauss-Newton vs. Gauss-Helmert[J]. Computational Statistics & Data Analysis, 2012, 56(12): 4470-4483. |
| [4] | OSADA E, OWCZAREK-WESOŁOWSKA M, SOŚNICA K. Gauss-Helmert model for total station positioning directly in geocentric reference frame including GNSS reference points and vertical direction from earth gravity model[J]. Journal of Surveying Engineering, 2019, 145(4): 04019013. |
| [5] | KOCH K R. Outlier detection for the nonlinear Gauss Helmert model with variance components by the expectation maximization algorithm[J]. Journal of Applied Geodesy, 2014, 8(3): 185-194. |
| [6] | WANG Bin, ZHAO Zhisheng, CHEN Yu, et al. A novel robust point cloud fitting algorithm based on nonlinear Gauss-Helmert model[J]. IEEE Transactions on Instrumentation Measurement, 2023, 72: 3239630. |
| [7] | KARGOLL B, OMIDALIZARANDI M, ALKHATIB H. Adjustment of Gauss-Helmert models with autoregressive and student errors[C]//Proceedings of 2020 Hotine-Marussi Symposium on Mathematical Geodesy. Cham: Springer, 2020: 79-87. |
| [8] | ZHU Jianjun, WANG Leyang, HU Jun, et al. Recent advances in the geodesy data processing[J]. Journal of Geodesy and Geoinformation Science, 2023, 6(3): 33-45. |
| [9] | 吕志鹏, 隋立芬. 基于非线性高斯-赫尔默特模型的结构总体最小二乘法[J]. 武汉大学学报(信息科学版), 2019, 44(12): 1808-1815. |
| LÜ Zhipeng, SUI Lifen. A structured total least squares method based on nonlinear Gauss-Helmert model[J]. Geomatics and Information Science of Wuhan University, 2019, 44(12): 1808-1815. | |
| [10] |
方兴, 曾文宪, 刘经南, 等. 基于非线性高斯-赫尔默特模型的混合整体最小二乘估计[J]. 测绘学报, 2016, 45(3): 291-296. DOI:.
doi: 10.11947/j.AGCS.2016.20150157 |
|
FANG Xing, ZENG Wenxian, LIU Jingnan, et al. Mixed LS-TLS estimation based on nonlinear Gauss-Helmert model[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(3): 291-296. DOI:.
doi: 10.11947/j.AGCS.2016.20150157 |
|
| [11] | 刘春阳, 刘超. 三维坐标转换的非线性Gauss-Helmert模型及其解法[J]. 测绘科学, 2017, 42(5): 118-123. |
| LIU Chunyang, LIU Chao. Nonlinear Gauss-Helment model and its solution for 3D coordinate transformation[J]. Science of Surveying and Mapping, 2017, 42(5): 118-123. | |
| [12] | WANG Bin, FANG Xing, LIU Chao, et al. Data snooping for the equality constrained nonlinear Gauss-Helmert model using sensitivity analysis[J]. Journal of Surveying Engineering, 2020, 146(4): 04020015. |
| [13] | KOCH K R. Robust estimations for the nonlinear Gauss Helmert model by the expectation maximization algorithm[J]. Journal of Geodesy, 2014, 88(3): 263-271. |
| [14] | 刘超, 王彬, 赵兴旺, 等. 三维坐标转换的高斯-赫尔默特模型及其抗差解法[J]. 武汉大学学报(信息科学版), 2018, 43(9): 1320-1327. |
| LIU Chao, WANG Bin, ZHAO Xingwang, et al. Three-dimensional coordinate transformation model and its robust estimation method under Gauss-Helmert model[J]. Geomatics and Information Science of Wuhan University, 2018, 43(9): 1320-1327. | |
| [15] | 赵志胜, 陈宇, 王彬. 利用非线性高斯-赫尔默特模型与抗差估计的点云拟合方法[J]. 武汉大学学报(信息科学版), 2024, 49(7): 1201-1211. |
| ZHAO Zhisheng, CHEN Yu, WANG Bin. Point cloud fitting method using the nonlinear Gauss-Helmert model and robust estimation[J]. Geomatics and Information Science of Wuhan University, 2024, 49(7): 1201-1211. | |
| [16] | 邝英才, 吕志平, 李林阳, 等. GNSS-A水下定位的动态非线性Gauss-Helmert模型及其抗差总体卡尔曼滤波算法[J]. 测绘学报, 2023, 52(4): 559-570. |
| KUANG Yingcai, LÜ Zhiping, LI Linyang, et al. Dynamic nolinear Gauss-Helmert model and its robust total Kalman filter algorithm for GNSS-acoustic underwater positioning[J]. Acta Geodaetica et Cartographica Sinica, 2023, 52(4): 559-570. | |
| [17] | KUANG Yingcai, LÜ Zhiping, WANG Fangchao, et al. A nonlinear Gauss-Helmert model and its robust solution for seafloor control point positioning[J]. Marine Geodesy, 2023, 46(1): 16-42. |
| [18] | VOGEL S, ERNST D, NEUMANN I, et al. Recursive Gauss-Helmert model with equality constraints applied to the efficient system calibration of a 3D laser scanner[J]. Journal of Applied Geodesy, 2022, 16(1): 37-57. |
| [19] | ZHOU Tengfei, LIN Peng, ZHANG Songlin, et al. A novel sequential solution for multi-period observations based on the Gauss-Helmert model[J]. Measurement, 2022, 193: 110916. |
| [20] | KARIMINEJAD M M, SHARIFI M A, AMIRI-SIMKOOEI A R. Tikhonov-regularized weighted total least squares formulation with applications to geodetic problems[J]. Acta Geodaetica et Geophysica, 2022, 57(1): 23-42. |
| [21] | 张勤, 黄观文. 非线性最小二乘理论及其在GPS定位中应用研究[M]. 北京: 测绘出版社, 2019. |
| ZHANG Qin, HUANG Guanwen. Research on nonlinear least squares theory and application in GPS positioning[M]. Beijing: Surveying and Mapping Press, 2019. | |
| [22] | 陶本藻, 张勤. GPS非线性数据处理的同伦最小二乘模型[J]. 武汉大学学报(信息科学版), 2003, 28(S1): 115-118. |
| TAO Benzao, ZHANG Qin. Homotopy least squares model for GPS nonlinear data processing[J]. Geomatics and Information Science of Wuhan University, 2003, 28(S1): 115-118. | |
| [23] | 张勤, 陶本藻. 基于同伦法的非线性最小二乘平差统一模型[J]. 武汉大学学报(信息科学版), 2004, 29(8): 708-710. |
| ZHANG Qin, TAO Benzao. Uniform model of nonlinear least squares adjustment based on homotopy method[J]. Geomatics and Information Science of Wuhan University, 2004, 29(8): 708-710. | |
| [24] | 胡志刚, 花向红, 李昭, 等. 基于同伦方法的非线性测量模型参数估计[J]. 武汉大学学报(信息科学版), 2008, 33(9): 930-933. |
| HU Zhigang, HUA Xianghong, LI Zhao, et al. Nonlinear surveying model parameters estimation based on homotopy arithmetic[J]. Geomatics and Information Science of Wuhan University, 2008, 33(9): 930-933. | |
| [25] | 胡志刚, 花向红, 李海英. 基于同伦算法的非线性坐标转换模型研究[J]. 测绘工程, 2008, 17(6): 24-28. |
| HU Zhigang, HUA Xianghong, LI Haiying. Non-linear coordinate transformation method based on homotopy arithmetic[J]. Engineering of Surveying and Mapping, 2008, 17(6): 24-28. | |
| [26] | 游为, 范东明, 黄瑞金. 适用于任意旋转角的三维直角坐标转换方法[J]. 测绘科学, 2009, 34(5): 154-155. |
| YOU Wei, FAN Dongming, HUANG Ruijin. A method of 3D rectangular coordinate transformation adapted to any rotation angle[J]. Science of Surveying and Mapping, 2009, 34(5): 154-155. | |
| [27] | 游为, 范东明. 基于改进同伦算法的非线性最小二乘平差[J]. 西南交通大学学报, 2009, 44(2): 181-185. |
| YOU Wei, FAN Dongming. Nonlinear least squares adjustment based on improved homotopy algorithm[J]. Journal of Southwest Jiaotong University, 2009, 44(2): 181-185. | |
| [28] | 欧阳全欢. 非线性同伦最小二乘理论研究及其应用[D]. 成都: 西南交通大学, 2010. |
| OUYANG Quanhuan. The study and application of nonlinear homotopy least squares theory[D]. Chengdu: Southwest Jiaotong University, 2010. | |
| [29] | 游为, 范东明, 傅淑娟. 同伦函数与填充函数相结合的非线性最小二乘平差模型[J]. 武汉大学学报(信息科学版), 2010, 35(2): 185-188. |
| YOU Wei, FAN Dongming, FU Shujuan. Nonlinear least squares adjustment based on homotopy functions and filled functions[J]. Geomatics and Information Science of Wuhan University, 2010, 35(2): 185-188. | |
| [30] | 刘伟科, 刘国林, 陶秋香. 基于同伦算法的非线性最小二乘相位解缠[J]. 测绘科学, 2012, 37(4): 126-128, 137. |
| LIU Weike, LIU Guolin, TAO Qiuxiang. Nonlinear least squares phase unwrapping based on homotopy method[J]. Science of Surveying and Mapping, 2012, 37(4): 126-128, 137. | |
| [31] | 唐利民, 朱建军. 不适定非线性最小二乘问题的正则化同伦法及其应用[J]. 大地测量与地球动力学, 2010, 30(6): 51-56. |
| TANG Limin, ZHU Jianjun. Regularized homotopy method for ill posed nonlinear least squares problems and its application[J]. Geodesy and Geodynamics, 2010, 30(6): 51-56. | |
| [32] | 唐利民. 非线性最小二乘的不适定性及算法研究[D]. 长沙: 中南大学, 2011. |
| TANG Limin. Research on the ill-posed and solving methods of nonlinear least squares problem[D]. Changsha: Central South University, 2011. | |
| [33] | 惠兴杰, 李霞, 陈一鸣. 一种新的基于Matlab环境的同伦路径跟踪算法[J]. 东北大学学报(自然科学版), 2007, 28(5): 620-622. |
| HUI Xingjie, LI Xia, CHEN Yiming. A new homotopic path-tracking algorithm based on Matlab[J]. Journal of Northeastern University (Natural Science), 2007, 28(5): 620-622. | |
| [34] | 王则柯, 高堂安. 同伦方法引论[M]. 重庆: 重庆出版社, 1990. |
| WANG Zeke, GAO Tang'an. An introduction to homotopy method[M]. Chongqing: Chongqing Publishing Group, 1990. | |
| [35] | 刘国林, 姜岩, 陶华学. 非线性最小二乘参数平差[J]. 测绘学报, 1998, 27(3): 38-44. |
| LIU Guolin, JIANG Yan, TAO Huaxue. Nonlinear least squares adjustment by parameters[J]. Acta Geodaetica et Cartographica Sinica, 1998, 27(3): 38-44. | |
| [36] | XUE shuqiang, YANG Yuanxi, DANG Yamin. Barycentre method for solving distance equations[J]. Survey Review, 2016, 48(348): 188-194. |
| [37] | 薛树强, 杨元喜, 党亚民. 测距定位方程非线性平差的封闭牛顿迭代公式[J]. 测绘学报, 2014, 43(8): 771-777. |
| XUE Shuqiang, YANG Yuanxi, DANG Yamin. A closed-form of Newton iterative formula for nonlinear adjustment of distance equations[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(8): 771-777. | |
| [38] | XU Peiliang. Fast and almost unbiased weighted least squares fitting of circles[J]. Measurement, 2023, 206: 112294. |
| [39] | FANG Xing. On non-combinatorial weighted total least squares with inequality constraints[J]. Journal of Geodesy, 2014, 88(8): 805-816. |
| [40] | WANG Bin, ZHAO Zhisheng, WANG Shuai, et al. Robust LS-VCE for the nonlinear Gauss-Helmert model: case studies for point cloud fitting and geodetic symmetric transformation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2024, 62: 3352920. |
| [41] | FANG Xing, HU Yu, ZENG Wenxian, et al. Weighted least-squares fitting of circles with variance component estimation[J]. Mea-surement, 2022, 205: 112132. |
| [42] | SNOW K B. Topics in total least-squares adjustment within the errors-in-variables model: singular cofactor matrices and prior information[D]. Columbus: The Ohio State University, 2012. |
| [43] | FANG Xing. Weighted total least squares solutions for applications in geodesy[D]. Hannover: Gottfried Wilhelm Leibniz Universität, 2011. |
| [44] | FANG Xing. Weighted total least squares: necessary and sufficient conditions, fixed and random parameters[J]. Journal of Geodesy, 2013, 87(8): 733-749. |
| [45] | HU Yu, FANG Xing, QIN Yuxin, et al. Weighted geometric circle fitting for the Brogar Ring: parameter-free approach and bias analysis[J]. Measurement, 2022, 192: 110832. |
| [1] | YAN Guangfeng, CEN Minyi. The identification method of gross error detection failpoint in L1-norm estimation [J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(11): 1430-1438. |
| [2] | LIU Zhiping, ZHU Dantong, YU Hang, ZHANG Kefei. Least-square variance-covariance component estimation method based on the equivalent conditional adjustment model [J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(9): 1088-1095. |
| [3] | CAI Yanhui, CHENG Pengfei, ZHANG Li, XU Yantian. Probabilities of two types of errors in sampling inspection for surveying and mapping products [J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(8): 954-959. |
| [4] | DENG Xingsheng, PENG Sichun, YOU Yangsheng. Weighted total least square adjustment EIO model and its algorithms [J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(7): 926-930. |
| [5] | WANG Leyang, YU Hang, ZOU Chuanyi, LU Tieding. EIV models and algorithms of weighted total least squares problem*: discuss with “Weighted total least square adjustment EIO model and its algorithms” [J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(7): 931-937. |
| [6] | SONG Yingchun, XIA Yuguo, XIE Xuemei. Adjustment model and algorithm based on ellipsoid uncertainty [J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(5): 555-562. |
| [7] | WANG Leyang, WEN Guisen. Bias-corrected variance components estimation of Partial EIV model [J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(4): 412-421. |
| [8] | LI Jianzhang, YAN Haowen. Parameter method data processing for CPⅢ precise trigonometric leveling network [J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(4): 431-438. |
| [9] | LI Bofeng, ZHANG Zhetao. Several Kinematic Data Processing Methods for Time-correlated Observations [J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(12): 1563-1570. |
| [10] | FANG Xing, HUANG Lixiong, ZENG Wenxian, WU Yun. On an Improved Iterative Reweighted Least Squares Algorithm in Robust Estimation [J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(10): 1301-1306. |
| [11] | WANG Zhizhong, SONG Yingchun, HE Lingli. Mixed Adjustment Algorithm for Part of the Coefficient Matrix with Uncertainty [J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(9): 1171-1178. |
| [12] | XIE Xuemei, SONG Yingchun, XIAO Zhaobing. Parameter Estimate Algorithm in Adjustment Model with Interval Constraint [J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(8): 1141-1147. |
| [13] | YU Hang, WANG Jian, WANG Leyang, NING Yipeng, LIU Zhiping. Total Kalman Filter Method of Dynamic EIV Model [J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(4): 480-489. |
| [14] | WANG Leyang, XIONG Luyun. A Method for Dealing with the Systematic Errors of Partial EIV Semi-parametric Model [J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(1): 25-34. |
| [15] | WANG Leyang, XU Guangyu, WEN Guisen. A Method for Partial EIV Model with Correlated Observations [J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(8): 978-987. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||